图解直接插入排序C语言实现
1 直接插入排序
直接插入排序类似于我们平时玩扑克牌时理牌的操作,以下面的图片为例:

如果使用直接插入排序方法理牌,则操作步骤为:
(1)将3放到最前面,此时牌的顺序为[3,5,4,6,2]
(2)将4放到3和5之间,此时牌的顺序为[3,4,5,6,2]
(3)将2放到最前面,此时牌的顺序为[2,3,4,5,6]
1.1 基本概念与原理
直接插入排序(Straight Insertion Sort)是一种基于逐个元素插入的简单排序算法,属于插入排序类的基本方法。其核心思想是通过将未排序元素依次插入已排序序列的适当位置实现整体有序化,特别适用于小规模或部分有序数据。
算法特性
稳定性:直接插入排序是稳定排序算法,相同元素的相对位置不会改变
原地性:仅需常数级别的额外空间(空间复杂度O(1)),属于原地排序
适应性:对部分有序数据效率较高,时间复杂度可降至O(n)
简单性:算法逻辑直观,易于理解和实现
1.2 算法执行过程
直接插入排序采用双层循环结构实现,具体执行步骤如下:
1.初始化阶段:
(1)将序列第一个元素视为已排序部分
(2)其余元素构成未排序部分
2.外层循环:
(1)从第二个元素开始遍历(索引i从1到n-1)
(2)将当前元素arr[i]作为待插入元素
3.内层循环(插入过程):
(1)从后向前扫描已排序部分(索引j从i-1到0)
(2)比较待插入元素与当前元素arr[j]
(3)若arr[j] > 待插入元素,则将arr[j]后移一位
(4)否则找到插入位置,结束内层循环
4.插入操作:
(1)将待插入元素放入正确位置
(2)已排序部分长度增加1
5.迭代重复:
重复步骤2-4,直到未排序部分为空
执行示例
以数组[5, 2, 4, 6, 1, 3]为例:
1.初始:插入2 → [2,5] | 4,6,1,3
2.[2,5] | 4,6,1,3 → 插入4 → [2,4,5] | 6,1,3
3.[2,4,5] | 6,1,3 → 插入6 → [2,4,5,6] | 1,3
4.[2,4,5,6] | 1,3 → 插入1 → [1,2,4,5,6] | 3
5.[1,2,4,5,6] | 3 → 插入3 → [1,2,3,4,5,6]
1.3 算法复杂度分析
时间复杂度
最坏情况:输入序列完全逆序,需n(n-1)/2次比较和移动
最好情况:输入序列已经有序,只需n-1次比较,0次移动
平均情况:随机序列下,平均需要n²/4次比较和移动
空间复杂度
O(1) - 仅需常数级别的额外空间用于存储临时变量
1.4 C语言实现直接插入排序
#include <stdio.h>#define SORT_DATA_TYPE int/*** @brief 打印数据** @param arr 数组* @param n 数组元素个数*/
void print_array(int arr[], int n)
{int i;for (i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}/*** @brief 直接插入排序** @param arr 待排序的数组* @param n 数组元素个数*/
void straight_insertion_sort(SORT_DATA_TYPE arr[], int n)
{SORT_DATA_TYPE temp;int i;int j;for (i = 1; i < n; i++){temp = arr[i];for (j = (i - 1); j >= 0; j--){if (arr[j] > temp){arr[j + 1] = arr[j];print_array(arr, n); /* 查看每次排序结构,调试使用 */}else{break;}}arr[j + 1] = temp;printf("第 %d 次插入排序结果:", i); /* 查看每次排序结构,调试使用 */print_array(arr, n); /* 查看每次排序结构,调试使用 */}
}int main()
{SORT_DATA_TYPE arr[] = {4, 3, 2, 1};int n = sizeof(arr) / sizeof(arr[0]);printf("old arr : ");print_array(arr, n);straight_insertion_sort(arr, n);printf("new arr : ");print_array(arr, n);return 0;
}
注:
不同类型的数组直接将SORT_DATA_TYPE全部替换为需要的类型,然后删除多余的宏定义即可支持任意类型数组的直接插入排序。
1.5 简单测试
通过使用2个数组[4,3,2,1]及[1,2,3,4]演示最坏情况和最好情况直接插入排序的执行过程:
最坏情况:
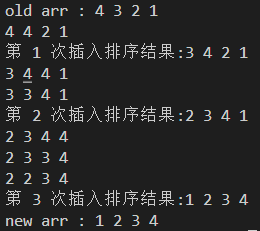
最坏情况需要进行n(n-1)/2次比较,也就是6次比较。可以使用如下图片演示这一过程:
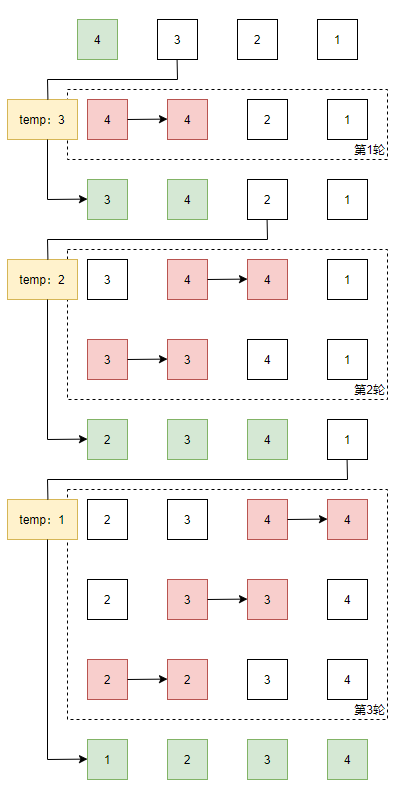
最好情况:
最好情况需要进行n-1次比较,也就是3次比较。

