当前位置：首页 > news >正文

抽象代数 · 代数结构 | 群、环、域、向量空间

news 2025/8/17 14:04:56

注：本文为 “抽象代数 · 代数结构” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未去重。
如有内容异常，请看原文。

代数结构入门：群、环、域、向量空间

2015-02-24 Updated: 2017-03-20 2,982

抽象代数研究对象是代数结构（集合 + 一套运算规则），以本人的理解方式整理了代数结构基础内容，旨在弄清群、环、域等代数结构间的关系。

1. 抽象代数

1.1 相关概念

数学的发展通常是先从简单的开始，然后不断放宽限制，推广到更一般化。从初等代数到抽象代数很好说明了这一点。

(1) 算术（arithmetic）

算术（arithmetic）无疑是数学中最古老、最基础和最初等的部分。算术研究数的性质及其运算。把数和数的性质、数和数之间的四则运算在应用过程中的经验累积起来，并加以整理，就形成了最古老的一门数学——算术 [1]。值得一提的是，算术运算不仅仅指加减乘除，还可以是百分比、平方根、取幂和对数；算法的对象包括自然数、整数、有理数和实数（兴许还包括复数）；进制不仅仅是十进制，还可以是二进制、十六进制、六十进制。算术的最大特点是关注具体数字。

(2) 初等代数

用符号（成了变量）代替具体的数字，就可以得到更一般化（ generalization ）的等式，举例如下：

$(2+3)2=22+2×2×3+32(3+5)2=32+2×3×5+52⇒(a+b)2=a2+2×a×b+b2\begin{align*} {{(2+3)}^{2}} & ={{2}^{2}}+2\times 2\times 3+{{3}^{2}} \\ {{(3+5)}^{2}} & ={{3}^{2}}+2\times 3\times 5+{{5}^{2}} \\ \Rightarrow {{(a+b)}^{2}} & ={{a}^{2}}+2\times a\times b+{{b}^{2}} \end{align*}$

图 1 从算术到代数的例子 [g](https://i-blog.csdnimg.cn/direct/4e97e537eca145a2a32542b4de80a47c.png =700x)

初等代数（elementary algebra）是古老算术的推广与发展。在古代，算术积累了大量数量问题的解法，为寻求更系统、更普遍的求解各种数量关系方法，就产生了以解方程为中心的初等代数 [2]。从实际问题的数量关系（即代数式：整式、分式、根式）、等量关系（或者不等式）列出列出方程或者方程组。方程（组）包括一元/二元一次方程（linear equations with one/two variable）、一元二次方程（quadratic equations）、指数和对数方程（exponential and logarithmic equations）、无理方程（radical equations）、线性方程组（system of linear equations）[3]。

高等代数相对于初等代数而言，本质上是一个东西，只是更加系统（深度 + 广度）。

初等代数再进一步推广（ generalization ），那就是抽象代数了。初等代数与抽象代数的界限在于初等代数只考虑实数和复数代数结构。摘录维基百科词条 Elementary algebra：

Unlike abstract algebra, elementary algebra is not concerned with algebraic structures outside the realm of real and complex numbers.

(3) 抽象代数

抽象代数（abstract algebra）、近世代数、现代代数（modern algebra）指的都是同一个意思（甚至直接称为代数学）。抽象代数主要研究对象是代数结构，包括群、环、域、向量空间。

伽罗瓦（Évariste Galois, 1811-1832）是现代群论的创始人（与阿贝尔独立发明），他利用群的概念彻底解决了用根式求解代数方程的可能性问题 [4]（称为伽罗瓦理论），系统阐释了为何五次以上之方程式没有公式解，而四次以下有公式解 [5]，使代数学从解方程的科学转变为研究代数结构的科学，即把代数推广到抽象代数 [4]。

(4) 线性代数

线性代数是抽象代数特殊的一类，其代数结构为：向量空间（vector spaces，也叫线性空间） + 线性变换（linear mappings）。很容易将线性代数和矩阵理论等同起来，但其实是不一样的，讨论线性变换是基于选定一组基的前提下。摘抄 mathoverflow 上的一个回答（原文在这里）：

When you talk about matrices, you’re allowed to talk about things like the entry in the 3rd row and 4th column, and so forth . In this setting, matrices are useful for representing things like transition probabilities in a Markov chain, where each entry indicates the probability of transitioning from one state to another.

In linear algebra, however, you instead talk about linear transformations, which are not a list of numbers , although sometimes it is convenient to use a particular matrix to write down a linear transformation. However, when you’re given a linear transformation , you’re not allowed to ask for things like the entry in its 3rd row and 4th column because questions like these depend on a choice of basis . Instead, you’re only allowed to ask for things that don’t depend on the basis, such as the rank, the trace, the determinant, or the set of eigenvalues. This point of view may seem unnecessarily restrictive, but it is fundamental to a deeper understanding of pure mathematics.

1.2 代数结构

既然抽象代数研究对象是代数结构（algebraic structure），那什么是代数结构呢。看了多个不同角度描述代数结构，如百度百科代数：代数是研究数、数量、关系与结构的数学分支。还是觉得《[转] MIT 牛人解说数学体系》中的描述最深入浅出，如下：

代数主要研究的是运算规则。一门代数，其实都是从某种具体的运算体系中抽象出一些基本规则，建立一个公理体系，然后在这基础上进行研究。一个集合再加上一套运算规则，就构成一个代数结构 [1] （想想计算机的数据结构：数据 + 操作）。

1.3 初等代数–> 抽象代数

抽象代数将初等代数的一些概念延伸。

(1) 数 –> 集合

集合在朴素集合论（naive set theory）和公理化集合论（axiomatic set theory）的定义是不一样的，前者指由一些元素组成；后者指具有某种特定性质事物的总体。还是看维基英文词条吧 [7]：

Rather than just considering the different types of numbers, abstract algebra deals with the more general concept of sets : a collection of all objects (called elements ) selected by property specific for the set.

(2) + –> 二元运算

加号 $+$ 被抽象为二元运算（binary operation），对两个元素作二元运算，得到的新元素仍然属于该集合，这叫封闭性（closure）。实际上，加减乘除都叫二元运算（二元指的是两个操作数）。原文如下 [7]：

The notion of addition (+) is abstracted to give a binary operation , $∗\ast$ say. The notion of binary operation is meaningless without the set on which the operation is defined. For two elements $a$ and $b$ in a set $S$ , $\ast b$ is another element in the set; this condition is called closure.

Addition (+), subtraction (-), multiplication (×), and division (÷) can be binary operations when defined on different sets , as are addition and multiplication of matrices, vectors, and polynomials.

(3) 0/1 –> 单位元

$0$ 和 $1$ 被抽象成单位元（identity elements）， $0$ 为加法单位元， $1$ 为乘法单位元。单位元是集合的一个特殊元素（跟二元运算有关），满足单位元与其他元素相结合时，不改变该元素，即满足 $\ast e = a$ 与 $\ast a = a$ 。可见，单位元取决于元素与二元运算，如矩阵的加法单位元是零矩阵，矩阵的乘法单位元是单位矩阵。值得注意的是，有些集合不存在单位元，如正整数集合（the set of positive natural numbers）没有加法单位元（no identity element for addition）。维基百科原文如下：

The numbers zero and one are abstracted to give the notion of an identity element for an operation. An identity element is a special type of element of a set with respect to a binary operation on that set. For a general binary operator $∗\ast$ the identity element $e$ must satisfy $\ast e = a$ and $\ast a = a$ . Not all sets and operator combinations have an identity element.

(4) 负数 –> 逆元素

负数推广到逆元素（inverse element），对于加法， $a$ 的逆元素是 $- a$ ；对于乘法， $a$ 的逆元素是倒数 $a^{-1}$ 。直观地说，逆元可以撤销操作，如加了一个数 $a$ ，再加上该数的逆元 $- a$ （相当于撤消操作），结果还是一样。维基百科原文如下：

The negative numbers give rise to the concept of inverse elements . For addition, the inverse of $a$ is written $- a$ , and for multiplication the inverse is written $a^{-1}$ . A general two-sided inverse element (left inverse + right inverse) $a^{-1}$ satisfies the property that $\ast a^{-1} = 1$ and $a−1∗a=1a^{-1} \ast a = 1$ .

The idea of an inverse element generalises concepts of a negation (sign reversal) in relation to addition, and a reciprocal in relation to multiplication. The intuition is of an element that can ‘undo’ the effect of combination with another given element . While the precise definition of an inverse element varies depending on the algebraic structure involved, these definitions coincide in a group.

(5) 结合律

结合律（Associative property）是某些二元运算的性质，有些二元运算没有结合律（如减法、除法、八元数）。原文如下：

Addition of integers has a property called associativity. That is, the grouping of the numbers to be added does not affect the sum . In general, this becomes $\ast b) \ast c = a \ast (b \ast c)$ . This property is shared by most binary operations, but not subtraction or division or octonion multiplication.

(6) 交换律

交换律（Commutative property），改变二元运算符两边的元素不影响结果。并不是所有二次元运算都满足交换律（如矩阵的乘法）。维基百科原文如下：

A binary operation is commutative if changing the order of the operands does not change the result. Addition and multiplication of real numbers are both commutative. In general, this becomes $\ast b = b \ast a$ .

This property does not hold for all binary operations. For example, matrix multiplication and quaternion multiplication are both non-commutative.

2. 类群结构（Group-like）

代数结构 $\ast)$ ，二元运算根据封闭性、单位元、逆元、结合律、交换律，可以归纳成不同的群。本节介绍的 group-like，从最不严格到严格（依次添加限制条件），其关系图如下：

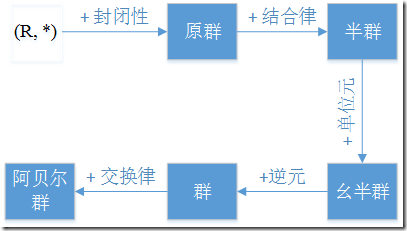
在这里插入图片描述

图 1 群之间的关系

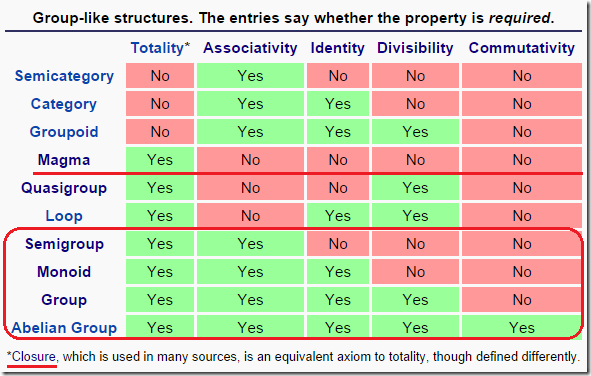
维基百科有一张表，给出更详细的 group-like 间的关系，如下：

在这里插入图片描述

2.1 原群

原群（magma）是一种基本的代数结构，只要满足两元素作二元运算得到新元素仍属于该集合，即封闭性。维基百科原文如下：

A magma is a basic kind of algebraic structure. Specifically, a magma consists of a set $M$ equipped with a single binary operation $\times M \rightarrow M$ . The binary operation must be closed by definition but no other properties are imposed .

2.2 半群

半群（Semigroup），满足结合律（associative property）的代数结构。 $\langle S, \ast \rangle$ ，其中二元运算 $∗\ast$ 是可结合的，即 $\ast b) \ast c = a \ast (b \ast c)$ ，则称 $V$ 是半群。维基百科原文如下：

A semigroup is an algebraic structure consisting of a set together with an associative binary operation.

A semigroup generalizes a monoid in that a semigroup need not have an identity element. It also (originally) generalized a group (a monoid with all inverses) in that no element had to have an inverse, thus the name semigroup .

2.3 幺半群

幺半群（monoid）在半群的基础上，还需要满足有一个单位元。维基百科原文如下：

A monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are semigroups with identity.

2.4 群

群（group）是两个元素作二元运算得到的一个新元素，需要满足群公理（group axioms），即：

封闭性： $\ast b$ is another element in the set
结合律： $\ast b) \ast c = a \ast (b \ast c)$
单位元： $\ast e = a$ and $\ast a = a$
逆元：加法的逆元为 $- a$ ，乘法的逆元为倒数 $1/ a$ ，…（对于所有元素）

如整数集合，二次元运算为加法就是一个群（封闭性是显然的，加法满足结合律，单位元为 $0$ ，逆元取相反数 $- a$ ）。维基百科原文如下：

A group is a set of elements together with an operation that combines any two of its elements to form a third element satisfying four conditions called the group axioms , namely closure , associativity , identity and invertibility .

One of the most familiar examples of a group is the set of integers together with the addition operation

2.5 阿贝尔群（交换群）

阿贝尔群（Abelian Group）在群的基础上，还需满足交换律。如整数集合和加法运算， $(Z,+)(\mathbb{Z}, +)$ ，是一个阿贝尔群。

群公理：见 2.4 群。
交换律： $a + b = b + a$

维基百科原文如下：

An abelian group , also called a commutative group , is a group in which the result of applying the group operation to two group elements does not depend on their order (the axiom of commutativity).

3. 环论

环在交换群基础上，进一步限制条件。环、交换环、域间的关系如下：

在这里插入图片描述

图 3 环、交换环、域间的关系

维基百科有一张表从不同角度呈现这三者的关系，如下：

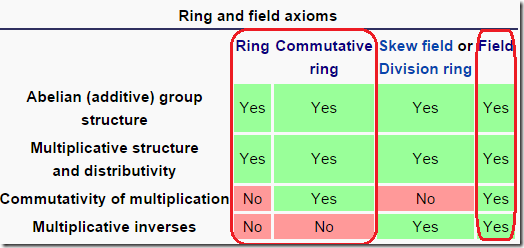
在这里插入图片描述

图 4 类环结构（Ring-like structures）（source from here）

3.1 环

环（ring）在阿贝尔群（也叫交换群）的基础上，添加一种二元运算 $⋅\cdot$ （虽叫乘法，但不同于初等代数的乘法）。一个代数结构是环 $\cdot)$ ，需要满足环公理（ ring axioms ），如 $(Z,+,⋅)(\mathbb{Z}, +, \cdot)$ 。环公理如下：

(1) $(R, +)$ 是交换群

封闭性： $a + b$ is another element in the set
结合律： $(a + b) + c = a + (b + c)$
单位元：加法的单位元为 $0$ ， $a + 0 = a$ and $0 + a = a$
逆元：加法的逆元为 $- a$ ， $a + (- a) = (- a) + a = 0$ （对于所有元素）
交换律： $a + b = b + a$

(2) $\cdot)$ 是幺半群

结合律： $\cdot b) \cdot c = a \cdot (b \cdot c)$
单位元：乘法的单位元为 $1$ ， $\cdot 1 = a$ and $\cdot a = a$

(3) 乘法对加法满足分配律

$\cdot (b + c) = (a \cdot b) + (a \cdot c)$ for all $a, b, c$ in $R$ （ left distributivity ）
$\cdot a = (b \cdot a) + (c \cdot a)$ for all $a, b, c$ in $R$ （ right distributivity ）

维基百科原文如下：

A ring is an abelian group with a second binary operation (The abelian group operation is called “ addition ” and the second binary operation is called “ multiplication ” in analogy with the integers) that is distributive over addition and is associative .

One familiar example of a ring is the set of integers. The integers are a commutative ring, since $a$ times $b$ is equal to $b$ times $a$ . The set of polynomials also forms a commutative ring. An example of a non-commutative ring is the ring of square matrices of the same size. Finally, a field is a commutative ring in which one can divide by any nonzero element: an example is the field of real numbers.

3.2 交换环

交换环（commutative ring）在环的基础上，二元运算乘法还满足交换律。

A commutative ring is a ring in which the multiplication operation is commutative

3.3 整环

整环（integral domain）在交换环的基础上，并满足没有零因子（如此，集合内任意两个元素乘积均不等于 $0$ ）。维基百科原文如下：

An integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibility. In an integral domain the cancellation property holds for multiplication by a nonzero element $a$ , that is, if $\neq 0$ , an equality $ab = a c$ implies $b = c$ .

4. 域

域（Field）在交换环的基础上，还增加了二元运算除法，要求元素（除零以外）可以作除法运算，即每个非零的元素都要有乘法逆元。由此可见，域是一种可以进行加减乘除（除 $0$ 以外）的代数结构，是数域与四则运算的推广。整数集合，不存在乘法逆元（ $1/3$ 不是整数），所以整数集合不是域。有理数、实数、复数可以形成域，分别叫有理数域、实数域、复数域。域的几种定义，直接看维基百科英文吧：

a field is a nonzero commutative ring that contains a multiplicative inverse for every nonzero element,

or equivalently a ring whose nonzero elements form an abelian group under multiplication.

As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division satisfying the appropriate abelian group equations and distributive law.

从有限域到交换环一些代数结构的从属关系如下：

Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ finite fields .

5. 向量空间

向量空间（vector space）是一些向量的集合。最熟悉的例子是几何向量或矢量（Euclidean vectors, geometric vector, spatial vector），表示具有大小和方向的对象，如 $AB→\overrightarrow{AB}$ 。矢量可以做加法（addition）和乘法（scalar multiplication）运算，举例如下：

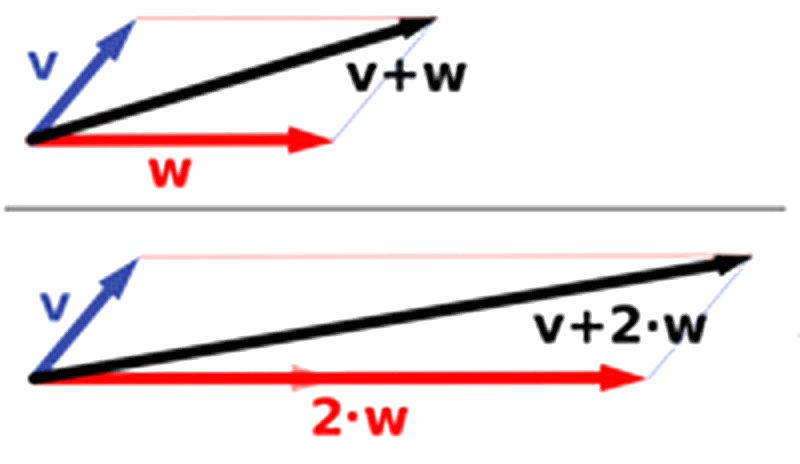
在这里插入图片描述

图 5 向量加法与数乘（Vector addition and scalar multiplication）（source from here）

其他例子，还包括坐标空间（Coordinate spaces）、复数、函数空间（Function spaces）、线性方程组（linear equations）。详情可查阅维基百科词条：Examples of vector spaces.

8 个公理

摘抄维基百科 Vector space 部分内容如下：

A vector space is a collection of objects called vectors , which may be added together and multiplied (“scaled”) by numbers, called scalars in this context. The operations of vector addition and scalar multiplication must satisfy certain requirements, called axioms , listed below.

给定域 $F$ ，向量空间 $V$ 记为 $F$ -向量空间。其二元运算：

向量加法： $\times V \rightarrow V$ 记作 $v + w$ , $∃v,w∈V\exists\ v, w \in V$
标量乘法： $⋅:F×V→V\cdot : F \times V \rightarrow V$ 记作 $a v$ , $∃a∈F\exists\ a \in F$ 且 $\in V$

并且满足如下 8 条公理 [10]：

向量加法结合律： $u + (v + w) = (u + v) + w$
向量加法的单位元： $V$ 存在零向量的 $0$ ， $∀v∈V\forall\ v \in V$ , $v + 0 = v$
向量加法的逆元素： $∀v∈V\forall\ v \in V$ , $∃w∈V\exists\ w \in V$ ，使得 $v + w = 0$
向量加法交换律： $v + w = w + v$
标量乘法与域乘法兼容性（compatibility）: $a (b v) = (ab) v$
标量乘法有单位元: $1 v = v$ , $1$ 指域 $F$ 的乘法单位元
标量乘法对于向量加法满足分配律： $a (v + w) = a v + a w$
标量乘法对于域加法满足分配律: $(a + b) v = a v + b v$

另，若 $F$ 是实数域 $R\mathbb{R}$ ，则 $V$ 称为实数向量空间；若 $F$ 是复数域 $C\mathbb{C}$ ，则 $V$ 称为复数向量空间；若 $F$ 是有限域，则 $V$ 称为有限域向量空间。

6. 模

模（module）是对向量空间的推广，将标量需为域（向量空间）推广到任意环（模）。维基百科 module 部分原文如下：

A module over a ring is a generalization of the notion of vector space over a field, where in the corresponding scalars are the elements of an arbitrary ring .
环上的模是域上向量空间概念的推广，其中对应的标量是任意环的元素。

7. 代数（环论）

代数（algebra）将 algebra over a field 中的域推广到交换环。维基百科原文如下：

An algebra over a commutative ring i s a generalization of the concept of an algebra over a field, where the base field $K$ is replaced by a commutative ring $R$ .

An algebra over a field is a vector space equipped with a bilinear product . An algebra such that the product is associative and has an identity is therefore a ring that is also a vector space, and thus equipped with a field of scalars. Such an algebra is called here a unital associative algebra for clarity, because there are also nonassociative algebras.

8. 格

格（lattice）是任意两个元素都有上确界和下确界的偏序集合。

A lattice is a partially ordered set in which every two elements have a unique supremum (also called a least upper bound or join) and a unique infimum (also called a greatest lower bound or meet).

An example is given by the natural numbers, partially ordered by divisibility, for which the unique supremum is the least common multiple and the unique infimum is the greatest common divisor.

9. 总结

是时候，祭出这张图了，图片来源于这里。YouTube 还有一段小视频讲这张图的，在这里。

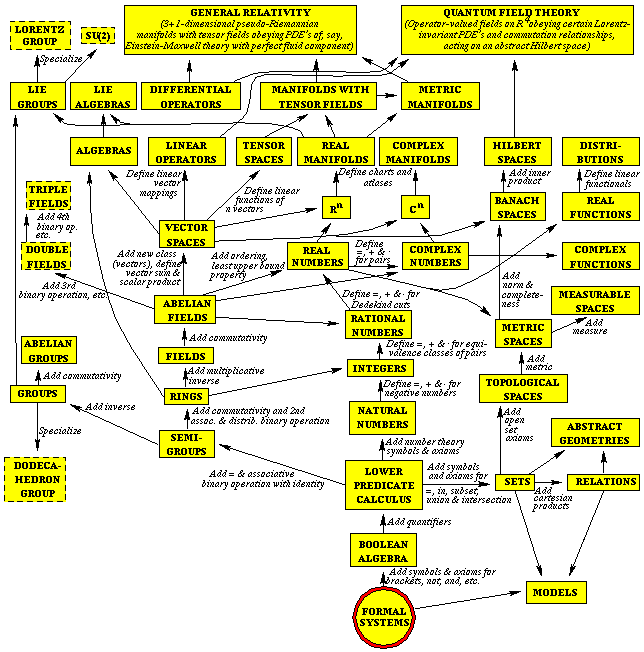
在这里插入图片描述

图 6 数学结构/对象（Mathematical Structures/Objects）

参考资料：

[1] 百度百科词条：算术

[2] 百度百科词条：初等代数

[3] Wikipedia: Elementary algebra

[4] 百度百科词条：抽象代数

[5] 百度百科词条：埃瓦里斯特・伽罗瓦

[6] [转] MIT 牛人解说数学体系

[7] Wikipedia: Algebra#Abstract_algebra

[8] 博文系列：明日枯荷包：数学闲话

[9] Wikipedia: Vector space

[10] 百度百科词条：向量空间

群环域

posted @ 2020-05-20 11:02 cyssmile

1. 初等代数到抽象代数的过渡

1.1 数到集合的推广

在朴素集合论（naive set theory）中，集合被定义为由若干元素组成的整体；而在公理化集合论（axiomatic set theory）中，集合被定义为具有某种特定性质的事物的全体，二者定义存在差异。

1.2 加法到二元运算的抽象

加号 “+” 可抽象为二元运算 “*”（binary operation）。若对集合中的任意两个元素实施该二元运算，所得结果仍属于该集合，则称此运算满足封闭性（closure）。事实上，加法、减法、乘法、除法均属于二元运算（“二元” 指运算需两个操作数）。

1.3 0 和 1 到单位元的扩展

0 与 1 可抽象为单位元（identity elements），其中 0 为加法单位元，1 为乘法单位元。单位元是与二元运算相关的集合中的特殊元素，其满足：对于集合中的任意元素，该元素与单位元进行二元运算后，结果仍为该元素，即满足 $a * e = a$ 且 $e * a = a$ 。单位元的具体形式由元素及二元运算决定，例如矩阵加法的单位元为零矩阵，矩阵乘法的单位元为单位矩阵。需要注意的是，部分集合不存在单位元，如正整数集合（the set of positive natural numbers）不存在加法单位元（no identity element for addition）。

1.4 负数到逆元素的推广

负数可推广为逆元素（inverse element）。对于加法运算，元素 $a$ 的逆元素为 $- a$ ；对于乘法运算，元素 $a$ 的逆元素为其倒数 $a^{-1}$ 。直观而言，逆元素可实现运算的撤销，例如对元素加上 $a$ 后，再加上其逆元素 $- a$ （相当于撤销之前的加法操作），结果与原元素一致。

1.5 结合律

结合律（Associative property）是部分二元运算具备的性质，并非所有二元运算都满足结合律，例如减法、除法及八元数的运算均不满足结合律。

1.6 交换律

交换律（Commutative property）指改变二元运算符两侧元素的位置，运算结果不变。但并非所有二元运算都满足交换律，如矩阵的乘法运算不满足交换律。

2. 类群结构

对于代数结构 $(R, *)$ ，依据二元运算所满足的封闭性、单位元、逆元、结合律、交换律等性质，可归纳出不同类型的群。本节所介绍的类群结构（group-like），按照从宽松到严格的顺序（依次添加限制条件），其关系如下：

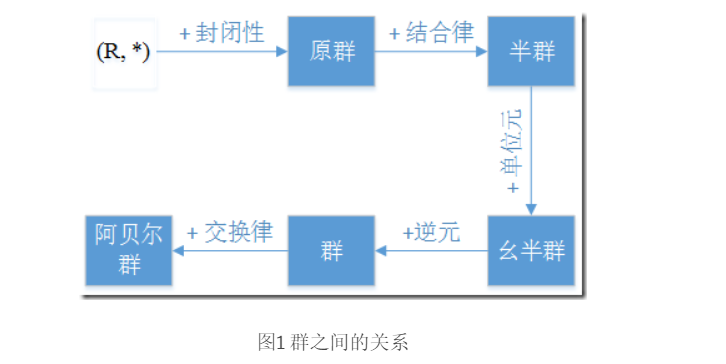
* 满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群；幺半群中所有元素存在逆元→群；群满足交换律→阿贝尔群*

图 1 群之间的关系

维基百科的表格更详细地呈现了类群结构间的关系，如下：
Group-like structures. The entries say whether the property is required.
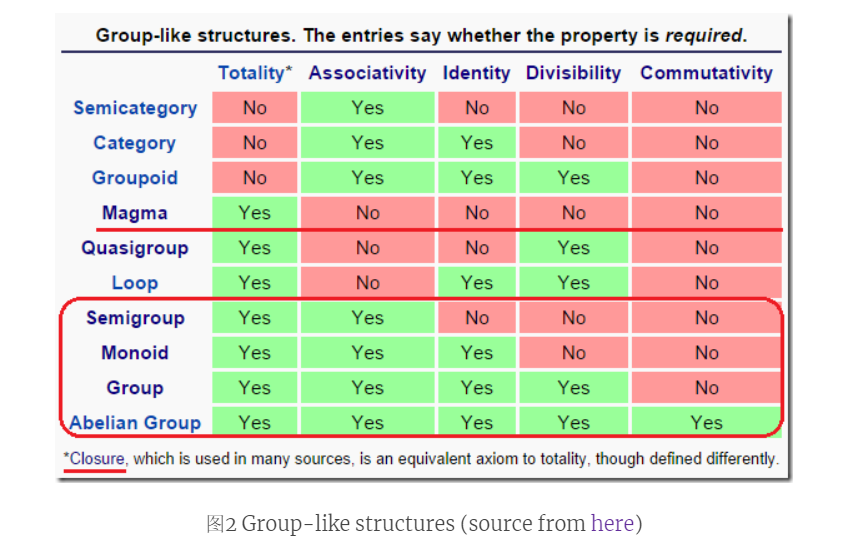
在这里插入图片描述

*Closure, which is used in many sources, is an equivalent axiom to totalit, though defined differently

图 2 Group-like structures (source from here)

2.1 原群

原群（magma）是一种基础代数结构，仅需满足：对集合中任意两个元素实施二元运算，所得结果仍属于该集合（即满足封闭性）。

2.2 半群

半群（Semigroup）是满足结合律（associative property）的代数结构。对于代数结构 $v =< S, * >$ ，若其中的二元运算满足结合律，即 $(a * b) * c = a * (b * c)$ ，则称 $V$ 为半群。

2.3 幺半群

幺半群（monoid）是在半群的基础上，进一步要求集合中存在单位元的代数结构。

2.4 群

群（group）是指在集合中定义的二元运算满足群公理（group axioms）的代数结构，即：

封闭性： $a * b$ 为集合中的另一个元素
结合律： $(a * b) * c = a * (b * c)$
单位元：存在元素 $e$ ，使得 $a * e = a$ 且 $e * a = a$
逆元：对于加法，逆元为 $- a$ ；对于乘法，逆元为倒数 $1/ a$ ，且集合中所有元素均存在逆元

例如，整数集合在加法运算下构成一个群（封闭性显然成立，加法满足结合律，单位元为 0，每个元素的逆元为其相反数 $- a$ ）。

2.4.1 群的严格定义

群 $G$ ，有时记为 ${G;⋅}\{G; \cdot\}$ ，是在集合上定义了二元运算 “ $⋅\cdot$ ” 的代数结构。对于集合 $G$ 中的任意序偶 $(a, b)$ ，通过该二元运算可生成 $G$ 中的元素 $\cdot b)$ ，且满足以下公理：

(A1) 封闭性：若 $a$ 和 $b$ 均属于 $G$ ，则 $\cdot b$ 也属于 $G$
(A2) 结合律：对于 $G$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，均有 $\cdot (b \cdot c) = (a \cdot b) \cdot c$ 成立
(A3) 单位元： $G$ 中存在元素 $e$ ，对于 $G$ 中的任意元素 $a$ ，均有 $\cdot e = e \cdot a = a$ 成立
(A4) 逆元：对于 $G$ 中的任意元素 $a$ ， $G$ 中存在元素 $a^{'}$ ，使得 $\cdot a' = a' \cdot a = e$ 成立

我们用 $N_{n}$ 表示包含 $n$ 个不同符号的集合，为便于表示，将其记为 ${1,2,⋯,n}\{1, 2, \cdots, n\}$ 。 $n$ 个不同符号的置换是指从 $N_{n}$ 到 $N_{n}$ 的一一映射。定义 $S_{n}$ 为 $n$ 个不同符号的所有置换组成的集合。

$S_{n}$ 中的每个元素均代表集合 ${1,2,⋯,n}\{1, 2, \cdots, n\}$ 的一个置换，且可验证 $S_{n}$ 构成一个群：

A1：若 $π,ρ∈Sn\pi, \rho \in S_{n}$ ，则合成映射 $π⋅ρ\pi \cdot \rho$ 是通过置换改变 $ρ\rho$ 中元素的次序形成的，例如 ${3,2,1}⋅{1,3,2}={2,3,1}\{3, 2, 1\} \cdot \{1, 3, 2\} = \{2, 3, 1\}$ ，显然 $π⋅ρ∈Sn\pi \cdot \rho \in S_{n}$
A2：映射的合成显然满足结合律
A3：恒等映射是不改变 $n$ 个元素位置的置换，对于 $S_{n}$ ，其单位元为 ${1,2,⋯,n}\{1, 2, \cdots, n\}$
A4：对于任意 $π∈Sn\pi \in S_{n}$ ，可抵消 $π\pi$ 所定义置换的映射即为 $π\pi$ 的逆元，且该逆元一定存在，例如 ${2,3,1}⋅{3,1,2}={1,2,3}\{2, 3, 1\} \cdot \{3, 1, 2\} = \{1, 2, 3\}$

若一个群包含的元素数量有限，则称其为有限群，该群的阶等于群中元素的个数；否则，称为无限群。

2.5 阿贝尔群（交换群）

阿贝尔群（Abelian Group）是在群的基础上，进一步满足交换律的代数结构。例如，整数集合与加法运算构成的代数结构 $(Z,+)(\mathbb {Z}, +)$ 是一个阿贝尔群，其满足交换律： $a + b = b + a$ 。

2.5.1 交换群的严格定义

若一个群满足以下条件，则称为交换群：

(A5) 交换律：对于群 $G$ 中的任意元素 $a$ 、 $b$ ，均有 $\cdot b = b \cdot a$ 成立

在加法运算下，整数集合（包括正整数、负整数和零）构成一个交换群；在乘法运算下，非零实数集合构成一个交换群。前文提及的集合 $S_{n}$ 是一个群，但当 $n > 2$ 时， $S_{n}$ 不是交换群。

当群中的运算符为加法时，其单位元为 0；元素 $a$ 的逆元为 $- a$ ；减法运算定义为： $a - b = a + (- b)$ 。

2.6 循环群

2.6.1 循环群的定义

在群中，幂运算定义为对群中运算的重复应用，例如 $a3=a⋅a⋅aa^{3} = a \cdot a \cdot a$ 。同时，定义 $a^{0} = e$ （ $e$ 为单位元），且 $a^{-n} = (a')^{n}$ （其中 $a^{'}$ 为 $a$ 在群中的逆元素）。若群中的每个元素均可表示为某个固定元素 $\in G)$ 的幂 $a^{k}$ （ $k$ 为整数），则称该群 $G$ 为循环群。此时，元素 $a$ 称为群 $G$ 的生成元，即 $a$ 生成群 $G$ 。循环群均为交换群，且可为有限群或无限群。

整数的加法群是一个无限循环群，由 1 生成。在此情形下，幂运算体现为加法的合成，即 $n$ 是 1 的 $n$ 次幂。

3. 环论

环是在交换群的基础上进一步添加限制条件形成的代数结构。环、交换环、域之间的关系如下：

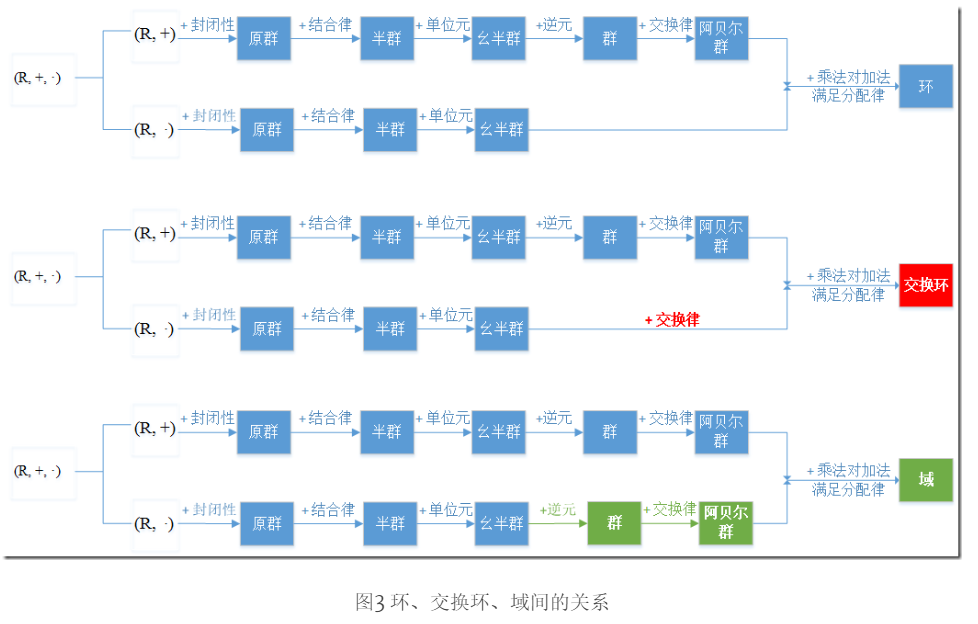
* 满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群；幺半群中所有元素存在逆元→群；群满足交换律→阿贝尔群中乘法对加法满足分配律→环满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群；幺半群中所有元素存在逆元→群；群满足交换律→阿贝尔群满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群；幺半群中所有元素存在逆元→群；群满足交换律且乘法对加法满足分配律→交换环满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群；幺半群中所有元素存在逆元→群；群满足交换律→阿贝尔群中乘法对加法满足分配律且非零元素有乘法逆元→域满足封闭性→原群；原群满足结合律→半群；半群存在单位元→幺半群；幺半群中所有元素存在逆元→群；群满足交换律→阿贝尔群*

图 3 环、交换环、域间的关系

维基百科的表格从不同角度呈现了这三者的关系，如下：
在这里插入图片描述
图 4 Ring-like structures (source from here)

3.1 环

环（ring）是在阿贝尔群（亦称交换群）的基础上，添加一种二元运算 “ $⋅\cdot$ ”（称为乘法，不同于初等代数中的乘法）形成的代数结构。代数结构 $\cdot)$ 为环需满足环公理（ring axioms），例如 $(Z,+,⋅)(\mathbb {Z}, +, \cdot)$ 是环。环公理如下：

$(R, +)$ 是交换群

封闭性： $a + b$ 为集合中的另一个元素
结合律： $(a + b) + c = a + (b + c)$
单位元：加法的单位元为 0，即 $a + 0 = a$ 且 $0 + a = a$
逆元：加法的逆元为 $- a$ ，即 $a + (- a) = (- a) + a = 0$ （对于所有元素）
交换律： $a + b = b + a$

$\cdot)$ 是幺半群

结合律： $\cdot b) \cdot c = a \cdot (b \cdot c)$
单位元：乘法的单位元为 1，即 $\cdot 1 = a$ 且 $\cdot a = a$

乘法对加法满足分配律（Multiplication distributes over addition）

$\cdot (b + c) = (a \cdot b) + (a \cdot c)$ 对所有 $\in R$ 成立（左分配律）
$\cdot a = (b \cdot a) + (c \cdot a)$ 对所有 $\in R$ 成立（右分配律）

3.1.1 环的严格定义

环 $R$ ，有时记为 ${R,+,×}\{R, +, \times\}$ ，是具有两个二元运算（分别称为加法和乘法）的集合，且对于 $R$ 中的任意元素 $a$ 、 $b$ 、 $c$ 满足以下公理：

(A1~A5) $R$ 关于加法构成交换群，即 $R$ 满足公理 A1 至 A5。对于该加法群，用 0 表示单位元，用 $- a$ 表示 $a$ 的逆元。
(M1) 乘法的封闭性：若 $a$ 和 $b$ 均属于 $R$ ，则 $\cdot b$ 也属于 $R$ 。
(M2) 乘法的结合律：对于 $R$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，有 $\cdot (b \cdot c) = (a \cdot b) \cdot c$ 成立。
(M3) 分配律：对于 $R$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，以下两式成立：
$\cdot (b + c) = a \cdot b + a \cdot c$
$\cdot c = a \cdot c + b \cdot c$

本质上，环是一个可在其上进行加法、减法 $[a - b = a + (- b)]$ 和乘法运算且运算结果仍在该集合内的集合。

实数上所有 $n$ 阶方阵的集合关于加法和乘法构成一个环。

3.2 交换环

$(R, +)$ 是交换群

封闭性： $a + b$ 为集合中的另一个元素
结合律： $(a + b) + c = a + (b + c)$
单位元：加法的单位元为 0，即 $a + 0 = a$ 且 $0 + a = a$
逆元：加法的逆元为 $- a$ ，即 $a + (- a) = (- a) + a = 0$ （对于所有元素）
交换律： $a + b = b + a$

$\cdot)$ 是幺半群

结合律： $\cdot b) \cdot c = a \cdot (b \cdot c)$
单位元：乘法的单位元为 1，即 $\cdot 1 = a$ 且 $\cdot a = a$

乘法对加法满足分配律（Multiplication distributes over addition）

$\cdot (b + c) = (a \cdot b) + (a \cdot c)$ 对所有 $\in R$ 成立（左分配律）
$\cdot a = (b \cdot a) + (c \cdot a)$ 对所有 $\in R$ 成立（右分配律）

若环满足以下条件，则称为交换环：

(M4) 乘法的交换律：对于 $R$ 中的任意元素 $a$ 、 $b$ ，有 $\cdot b = b \cdot a$ 成立。

偶整数集合（包括正偶数、负偶数和 0）记为 $S$ ，在普通加法和乘法运算下构成交换环。前文定义的所有 $n$ 阶方阵的集合不构成交换环。整数 ${0,1,⋯,n−1}\{0, 1, \cdots, n-1\}$ 的集合 $Zn\mathbb {Z}_{n}$ 结合模 $n$ 的算术运算构成交换环。

3.3 整环

整环（integral domain）是在交换环的基础上，进一步满足无零因子条件（即集合中任意两个元素的乘积均不为 0）的代数结构。

整环的定义为满足以下公理的交换环：

(M5) 乘法单位元： $R$ 中存在元素 1，对于 $R$ 中的任意元素 $a$ ，有 $\cdot 1 = 1 \cdot a = a$ 成立。
(M6) 无零因子：若 $R$ 中存在元素 $a$ 、 $b$ ，且 $\cdot b = 0$ ，则必有 $a = 0$ 或 $b = 0$ 。

在普通加法和乘法运算下，整数集合（包括正整数、负整数和 0）记为 $S$ ，则 $S$ 是一个整环。

4. 域

域（Field）是在交换环的基础上，添加二元运算除法后形成的代数结构，要求除零以外的所有元素均可进行除法运算，即每个非零元素都有乘法逆元。因此，域是一种可进行加减乘除（除 0 以外）运算的代数结构，是数域与四则运算的推广。整数集合中不存在乘法逆元（如 $1/3$ 不是整数），故整数集合不是域。有理数、实数、复数可分别形成有理数域、实数域、复数域。

4.1.1 域的严格定义

域 $F$ ，有时记为 ${F,+,×}\{F, +, \times\}$ ，是具有两个二元运算（分别称为加法和乘法）的集合，且对于 $F$ 中的任意元素 $a$ 、 $b$ 、 $c$ 满足以下公理：

(A1~M6) $F$ 是整环，即 $F$ 满足公理 A1 至 A5 以及公理 M1 至 M6。
① 通常，乘法不用 “ $×\times$ ” 表示，而是用两个元素的连接表示。
(M7) 乘法逆元：对于 $F$ 中除 0 以外的任意元素 $a$ ， $F$ 中存在元素 $a^{-1}$ ，使得 $\cdot a^{-1} = (a^{-1}) \cdot a = 1$ 成立。

本质上，域是一个可在其上进行加法、减法、乘法和除法运算且运算结果仍在该集合内的集合。除法定义为： $\cdot (b^{-1})$ 。

有理数集合、实数集合和复数集合都是常见的域的例子。需要说明的是，所有整数的集合不是域，因为并非集合中所有元素都有乘法逆元；实际上，整数集合中仅有元素 1 和 $- 1$ 存在乘法逆元。

进一步理解后，域 ${F,+,⋅}\{F, +, \cdot\}$ 也可描述为：定义了加法和乘法两种二元运算的集合，且满足以下条件：

$F$ 关于加法构成交换群。
除去零元素， $F$ 关于乘法构成交换群。
分配律成立，即对于 $F$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，有
$\cdot (b + c) = a \cdot b + a \cdot c\\ (a + b) \cdot c = a \cdot c + b \cdot c$

从有限域到交换环的代数结构从属关系如下：

Commutative rings ⊇ integral domains ⊇ integral closed domains ⊇ unique factorization domains ⊇ principal ideal domains ⊇ Euclidean domains ⊇ fields ⊇ finite fields.

交换环 ⊇ 整环 ⊇ 整闭整环 ⊇ 唯一分解整环 ⊇ 主理想整环 ⊇ 欧几里得整环 ⊇ 域 ⊇ 有限域。

总结

在这里插入图片描述

(A1) 加法的封闭性：若 $a$ 和 $b$ 属于 $S$ ，则 $a + b$ 也属于 $S$
(A2) 加法结合律：对于 $S$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，有 $a + (b + c) = (a + b) + c$
(A3) 加法单位元： $R$ 中存在元素 0，对于 $S$ 中的任意元素 $a$ ，有 $a + 0 = 0 + a = a$
(A4) 加法逆元：对于 $S$ 中的任意元素 $a$ ， $S$ 中存在元素 $- a$ ，使得 $a + (- a) = (- a) + a = 0$
(A5) 加法交换律：对于 $S$ 中的任意元素 $a$ 和 $b$ ，有 $a + b = b + a$
(M1) 乘法的封闭性：若 $a$ 和 $b$ 属于 $S$ ，则 $\cdot b$ 属于 $S$
(M2) 乘法结合律：对于 $S$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，有 $\cdot (b \cdot c) = (a \cdot b) \cdot c$
(M3) 分配律：对于 $S$ 中的任意元素 $a$ 、 $b$ 、 $c$ ，有 $\cdot (b + c) = a \cdot b + a \cdot c， (a + b) \cdot c = a \cdot c + b \cdot c$
(M4) 乘法交换律：对于 $S$ 中的任意元素 $a$ 和 $b$ ，有 $\cdot b = b \cdot a$
(M5) 乘法单位元：对于 $S$ 中的任意元素 $a$ ， $S$ 中存在元素 1，使得 $\cdot 1 = 1 \cdot a = a$
(M6) 无零因子：对于 $R$ 中的元素 $a$ 、 $b$ ，若 $\cdot b = 0$ ，则必有 $a = 0$ 或 $b = 0$
(M7) 乘法逆元：若 $a$ 属于 $S$ 且 $\neq 0$ ，则 $S$ 中存在元素 $a^{-1}$ ，使得 $\cdot a^{-1} = (a^{-1}) \cdot a = 1$

via：

代数结构入门：群、环、域、向量空间 | | Spark & Shine
https://sparkandshine.net/algebraic-structure-primer-group-ring-field-vector-space/
群环域 - cyssmile - 博客园
https://www.cnblogs.com/cyssmile/p/12922390.html

查看全文

http://www.dtcms.com/a/335197.html