洛谷B3865 [GESP202309 二级] 小杨的 X 字矩阵(举一反三)
题目描述
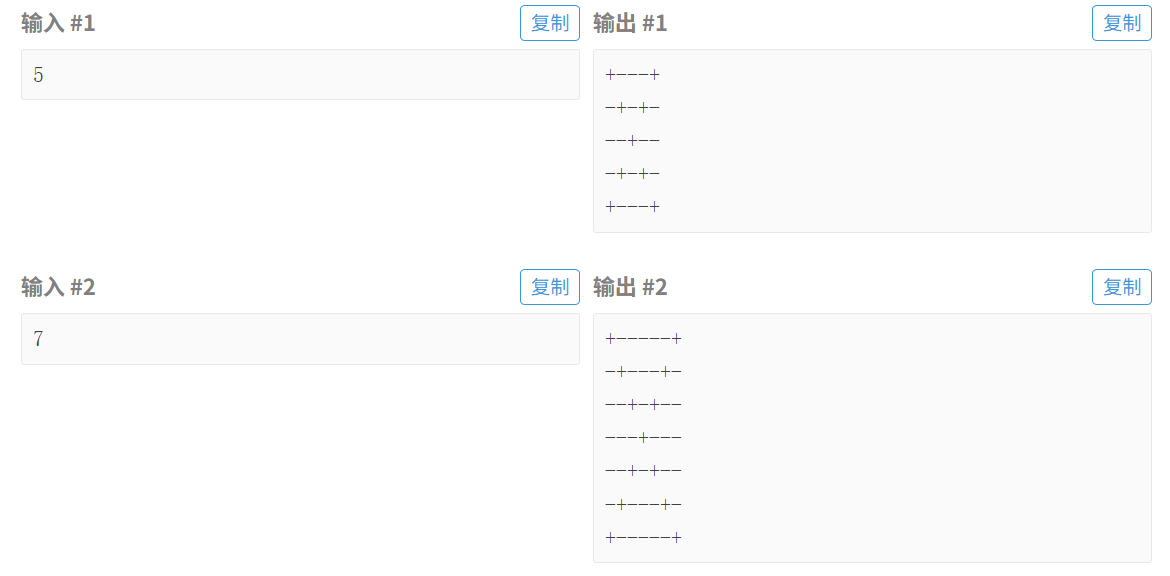
小杨想要构造一个 X 字矩阵( 为奇数),这个矩阵的两条对角线都是半角加号 + ,其余都是半角减号 - 。例如,一个 5×5 的 X 字矩阵如下:
+---+
-+-+-
--+--
-+-+-
+---+
请你帮小杨根据给定的 打印出对应的“X 字矩阵”。
输入格式
一行一个整数 ( 5≤N≤49,保证为奇数)。
输出格式
输出对应的“X 字矩阵”。
请严格按格式要求输出,不要擅自添加任何空格、标点、空行等任何符号。你应该恰好输出 N 行,每行除了换行符外恰好包含 N 个字符,这些字符要么是 +,要么是 -。
输入输出样例
说明/提示
特别提醒
在常规程序中,输入、输出时提供提示是好习惯。但在本场考试中,由于系统限定,请不要在输入、输出中附带任何提示信息。
题目链接地址:B3865 [GESP202309 二级] 小杨的 X 字矩阵 - 洛谷
解题思路
对于这类矩阵图形的输出,要求一定要熟练掌握,并能举一反三解决类似问题(如Z字形、日字形、H形等)。
1. 观察规律(从具体到抽象)
目标:发现X形矩阵中+和-的位置规律。
方法:用可视化例子引导思考:
# 5×5 的X形矩阵(行号i从1开始,列号j从1开始)
+---+ # 第1行:i=1,主对角线(i=j=1) 或 副对角线(i+j=1+5=6)
-+-+- # 第2行:i=2,满足i=j=2 或 i+j=2+4=6
--+-- # 第3行:i=3,两对角线交叉,可以表示为i=j=3,或者i+j=6
-+-+- # 第4行:i=4,主对角线i=j=4,或副对角线i+j=4+2=6
+---+ # 第5行:i=5,主对角线i=j=5,或副对角线i+j=5+1
思考:
- 主对角线上的+满足什么条件?(行号i等于列号j)
- 副对角线上的+满足什么条件?(行号i加列号j等于N+1)
- 其他位置是什么符号?(-)
2. 数学建模(规律转公式)
目标:将观察到的规律转化为数学条件。
核心结论:
- 输出“+“”的条件:i == j 或 i + j == N +1
- 否则输出‘’-‘’
验证:对于5×5矩阵的中心点(3,3):同时满足i==j和i+j==6,仍正确
3、代码实现(分步拆解)
目标:将数学条件转化为代码,强调循环嵌套和条件判断。
关键点:
(1)输入矩阵大小 n
题目保证 N 是 5~49 的奇数,所以不需要额外检查。
(2)双重循环遍历矩阵
外层循环 for (int i = 1; i < =N; i++):控制行号 i,从 1到 N。
内层循环 for (int j = 1 j < =N; j++):控制列号 j,从 1到 N。
(3)条件判断(判断是否在对角线上)
主对角线:行号 i 等于列号 j(即 i == j)。
副对角线:行号 i 加列号 j 等于 N+1(即 i + j == N+1)。
如果满足任意一个条件,输出 '+',否则输出 '-'。
(4)输出控制(换行处理)
每行结束后使用 cout << endl; 换行。
代码
#include <iostream>
using namespace std;
int main(){int N;cin>>N;for(int i=1;i<=N;i++){for(int j=1;j<=N;j++){if(i==j||i+j==N+1)cout<<'+';else cout<<'-';}cout<<endl;}return 0;
}举一反三(扩展思维)
变形问题:思考其他类似图形如何实现
1. Z字形矩阵:
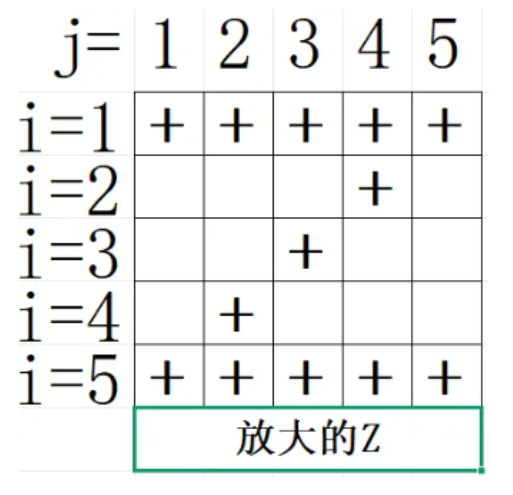
第一行和最后一行全 +,中间行仅副对角线 +。
if (i == 0 || i == N || i + j == N+1) {
cout << '+';
} else {
cout << '-';
}
2. 空心矩形:
仅最外层 +,内部 -。
if (i == 0 || i == N || j == 0 || j == N) {
cout << '+';
} else {
cout << '-';
}
3. N字矩阵

第一列和最后一列全 +,中间列仅对角线 +。
if(j == 1 || j == N || j == i){
cout << "+";
}else{
cout << "-";
常见错误
- 边界错误:可能混淆n和n-1(从0开始还是1开始)
- 条件遗漏:忘记用or合并两条对角线。
- 输出格式:忘记换行。
