洛谷B3924 [GESP202312 二级] 小杨的H字矩阵
题目描述
小杨想要构造一个 N×N 的 H 字矩阵(N 为奇数),具体来说,这个矩阵共有 N 行,每行 N 个字符,其中最左列、最右列都是 | ,而中间一行(即第 (N+1)/2 行)的第 2∼N−1 个字符都是 - ,其余所有字符都是半角小写字母 a。例如,一个 N=5 的 H 字矩阵如下:

请你帮小杨根据给定的 N 打印出对应的“H 字矩阵”。
输入格式
一行一个整数 N(5≤N≤49 ,保证 N 为奇数)。
输出格式
输出对应的“H 字矩阵”。
请严格按格式要求输出,不要擅自添加任何空格、标点、空行等任何符号。你应该恰好输出 N 行,每行除了换行符外恰好包含 N 个字符,这些字符要么是 - ,要么是 | ,要么是 a 。你的输出必须和标准答案完全一致才能得分,请在提交前仔细检查。
输入输出样例
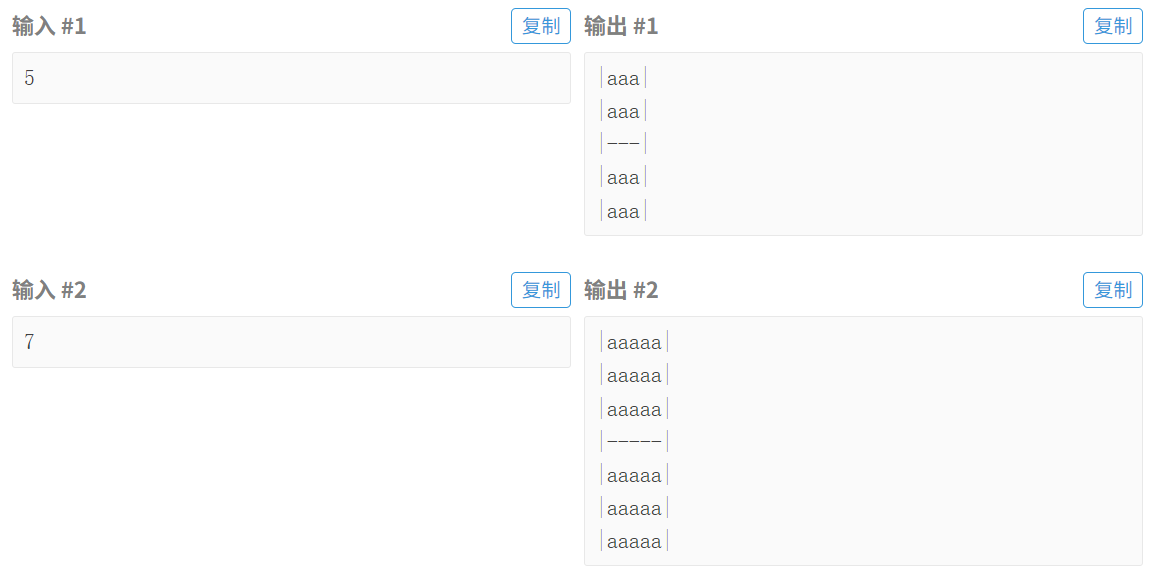
B3924 [GESP202312 二级] 小杨的H字矩阵 - 洛谷 https://www.luogu.com.cn/problem/B3924
解题思路
参考小杨的 X 字矩阵(举一反三)
我前一篇文章曾用行列号关系解决X矩阵,那么H矩阵是否也能用类似方法呢?哪些条件需要调整?
特征 X 字矩阵 H 字矩阵
图形结构 两条对角线交叉 两竖线 + 一条水平线
核心规律 i == j 或 i + j == N+1 j == 0 或 j == N 或 i == 中心行(N+1)/2
符号分配 对角线+,其余- 边界| ,中间行-,其余a
同X矩形不同的是,此题用到了三种字符输出 ,所以需要考虑三种情况,所以用到了if...else if...else结构。
数学建模(条件分解)
目标:将规律转化为逻辑条件,强调 分层判断:
-
边界列:
j == 1 || j == N→'|' -
中心行:
i == (N+1)/2且j > 1 && j < N→'-' -
默认填充:其余情况 →
'a'
公式化表示:
if (j == 1 || j == N)
cout << '|';
else if (i == (N+1) / 2)
cout << '-';
else cout << 'a';
代码实现
#include <iostream>
using namespace std;
int main(){int N;cin>>N;for(int i=1;i<=N;i++){for(int j=1;j<=N;j++){if(j==1||j==N) cout<<'|';else if(i==(N+1)/2) cout<<'-';elsecout<<'a';}cout<<endl;}return 0;
}-
条件优先级:先检查列边界,再处理中心行,最后默认情况。
举一反三(扩展思考)
变形问题:尝试其他字母矩阵:
1. T 字矩阵:
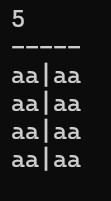
第一行全 -,中间列全 |,其余 a。
if(i==1) cout<<'-';
else if(j==(1+N)/2) cout<<'|';
else cout<<'a';
2. 十字矩阵:
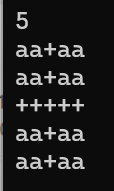
中心行和中心列为 +,其余 a(结合X和H的思路)。
if(i==(1+N)/2||j==(1+N)/2) cout<<'+';
else cout<<'a';
3. 日字矩阵

if(j==1||j==N) cout<<'|';
else if(i==1||i==N||i==(1+N)/2) cout<<'-';
else cout<<'x';
方法论总结
- 观察图形分层(边界、中心行/列、填充区)。
- 用行列号建立条件(类似坐标轴思维)。
- 按优先级编写判断逻辑(边界优先,特殊区域次之)。
与X矩阵的对比总结
维度 X 字矩阵 H 字矩阵
核心条件 对角线关系(i±j) 列边界 + 中心行固定值
符号逻辑 两条线交叉 三部分独立判断
思维扩展 适用于斜线类图形(如Z、菱形) 适用于横纵线组合(如T、工字形)
通过这种对比,能更深刻理解 “行列号定位法” 的通用性,并灵活迁移到其他矩阵问题中。
