线性代数之两个宇宙文明关于距离的对话
基变换
在线性代数的学习中,n维空间中的n维向量的元素常常是由相对独立的因素组成的,这些相对独立的因素或者完全独立(垂直或者正交),或者相对独立(线性无关,我有你没有的部分)。对于n维空间的几何图形的想象,坐标轴的现实意义上的垂直不是必须的,如果几何意义上的垂直或者正交代之以代数意义上的线性无关概念,取消了几何作图对垂直的要求,我们的平面就可以通过斜坐标系画出来了,就可以形象理解了由n个线性无关向量张成的n维空间的理论,进而想象高维空间的图像也就不是一件特别困难的事情了。
空间本身并没有内蕴的网格,每种基下的宇宙空间生物都可以按照基的方向绘制自己的网格,是有助于帮助理解它所在的空间的工具,网格是主观的,不同的网格空间通过变换达到对方的网格,实现坐标系的切换。因为所有的向量乘以0都是零向量,不同的坐标系下的宇宙生物对0向量的位置可以达成共识。

空间中的两个点决定了一个自由向量,把所有自由向量的初始点全部拉到坐标原点,这样平面中的任意一个点就可以和一个向量对应上了(用群的观点看,是一种自由向量和笛卡尔坐标系中点的之间的同构)。
自由向量的坐标是可以看成是2个标量,这两个标量的值和坐标系基的选取有直接关系,因为基向量正是这两个标量缩放的对象。
可以把基向量看成是隐藏于空间坐标系网格中的隐含假设,基变换是说,任何两个线性无关的向量都可以作为新的坐标系的基定义新的网格,并通过将新基定义为完成加冕。
无论新基是否正交,我们都可以在该坐标系下将基向量自身视为。坐标系切换的本质就是重新定义“单位向量”,与基的正交性无关。非正交性仅导致内积计算不同,但线性变换的代数描述完全自洽。
只要不涉及角度,距离等的度量,可以将任意两个线性无关的向量作为(1,0)和(0,1)而产生新的坐标宇宙,因为这两个向量就是定义坐标(1,0)和(0,1)含义的向量。
一个很自然的问题是,我们如何在不同基下进行坐标变换?
坐标变换
问题,在基下的坐标向量(-1,2),如何变换成我们的坐标系下的坐标?
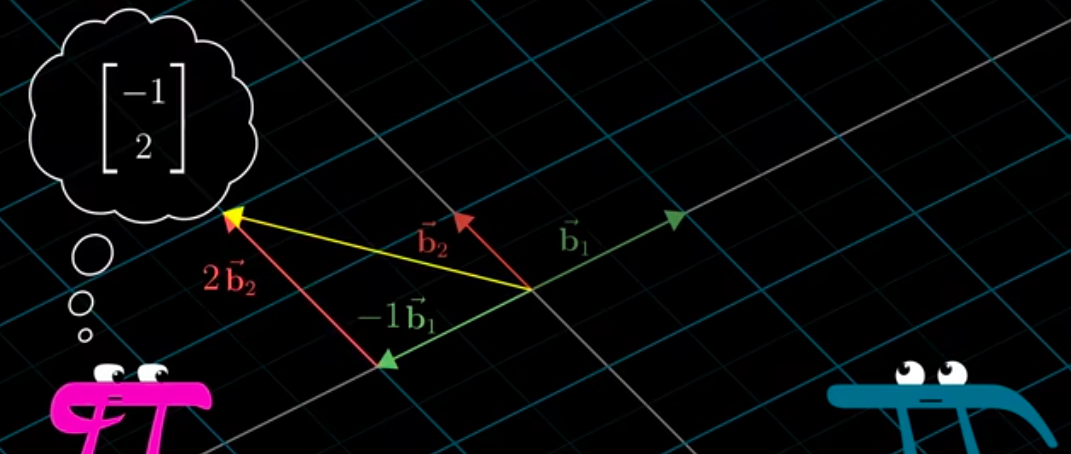
转换到我们的坐标系下:
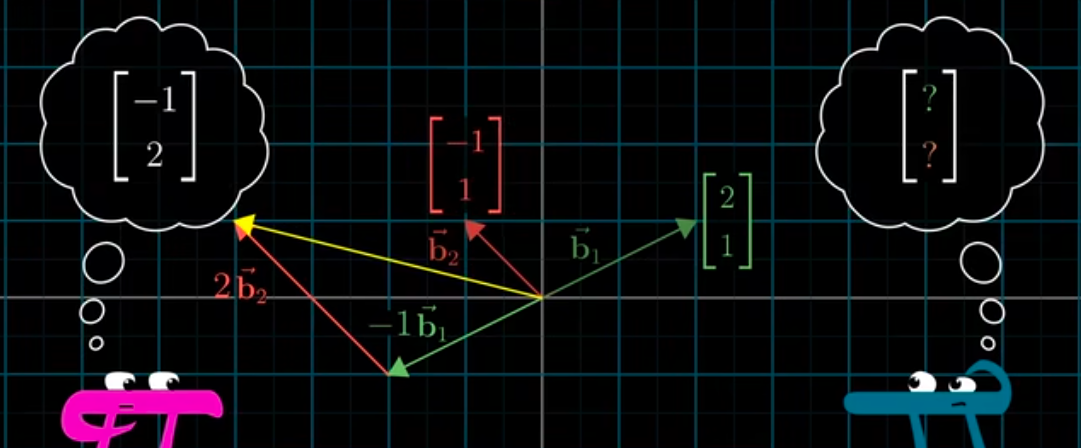
就可以得到我们的坐标系下的坐标了:
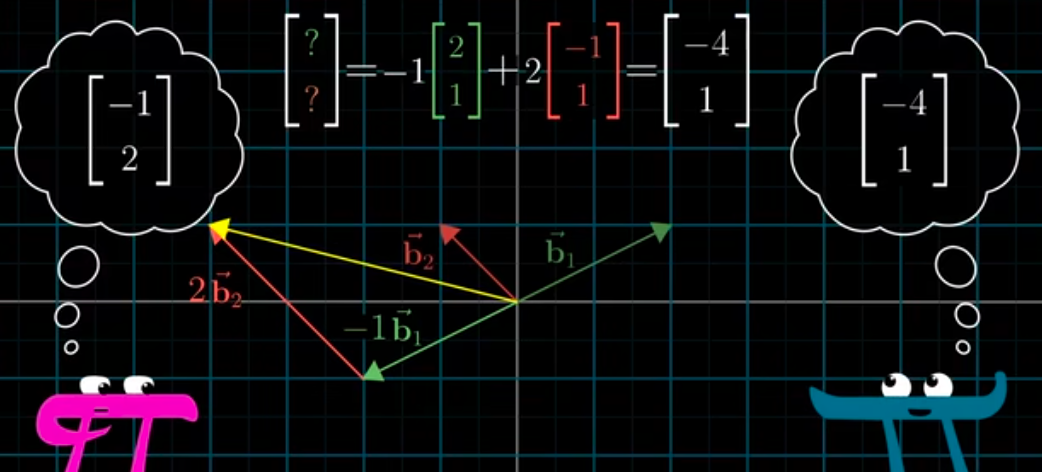 线性变换的一个重要特性在于,变换后的向量仍旧是相同的线性组合,不过使用的是新的基向量。
线性变换的一个重要特性在于,变换后的向量仍旧是相同的线性组合,不过使用的是新的基向量。
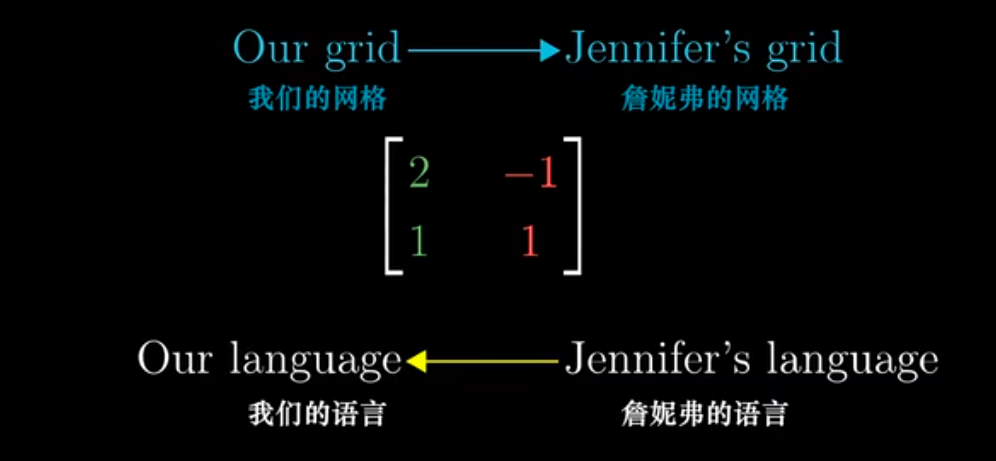
垂直的绝对性
前面提到了可以将非正交的基看成是(1,0)和(0,1)而不会产生自洽问题,但是线性代数中明明学过,两个垂直的向量其内积为0,内积的计算方式是两个向量的坐标点乘,所以如果新的非正交坐标系可以看作是(1,0)和(0,1),其坐标点积为0,推导出内积为0,说明两个坐标系垂直,但是前提明明是新基非正交的呀?矛盾。

其实,上面的逻辑链条中存在一个问题,在非正交基下,内积不再等于两个向量的坐标点乘,也就是说,在任何坐标系下,内积为0确实表示向量互相垂直,但是在非正交基下,内积就不能通过坐标的点积进行计算了,点积计算的结果和基的选择有直接关系。
在包括非正交形式的任何基变换下,垂直都是绝对的,垂直由真实内积 ⟨u,v⟩=0定义,在任何坐标系下对应90°夹角。
实际上,内积的完整计算公式是:
其中G是度规矩阵,在标准正交基下,G是单位矩阵,所以可以内积计算公式蜕化为线性代数课本上介绍的:
而在非正较基下,其空间中的两个向量的
内积计算公式为:
为了计算G,我们先将非标准坐标系下的向量转换回原正交坐标系:
因为原坐标系正交,可以直接用坐标点乘得到真实内积:
代入:
所以,最终得到度规矩阵G的表达式如下,可以看到其是一个对称矩阵:
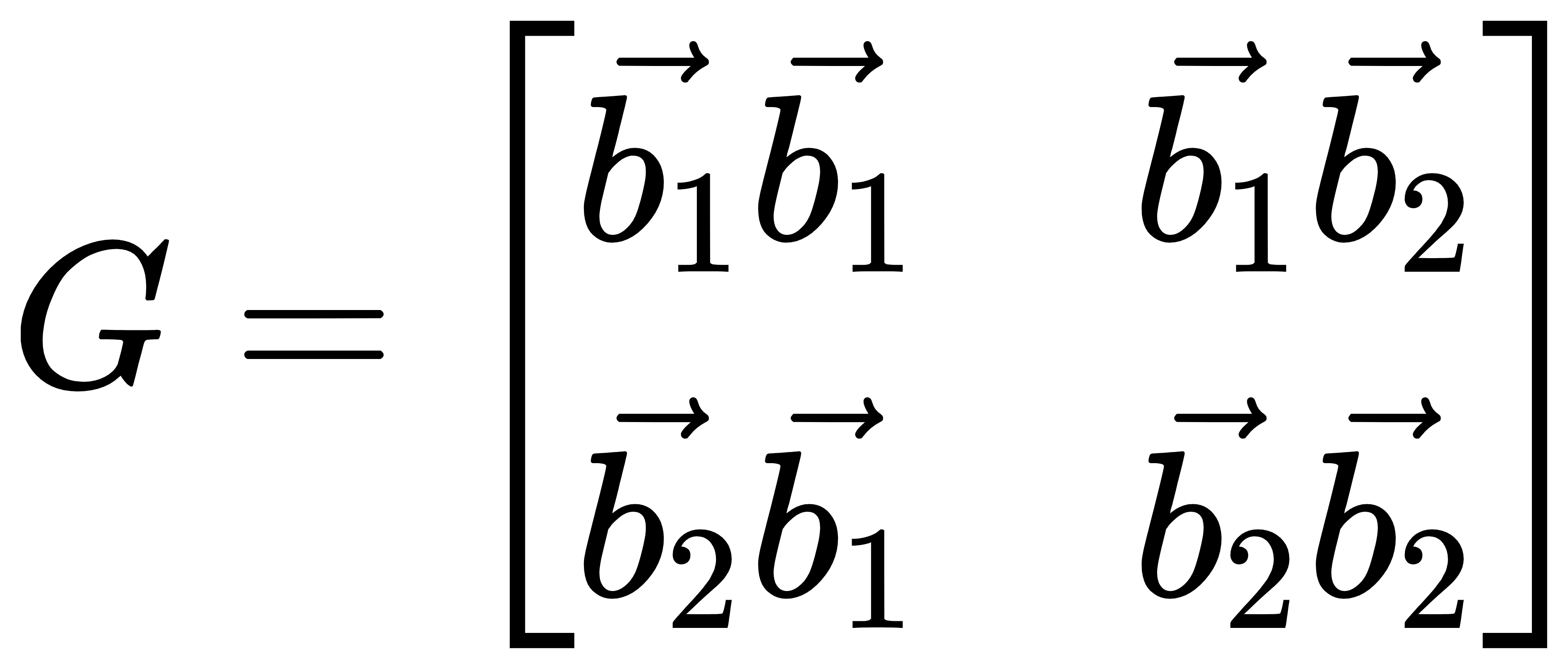
考虑到非正交坐标系,则任意向量的长度公式变为:
在非正交基下,坐标点积为零的向量不一定实际垂直。其实际夹角由度量矩阵G修正:
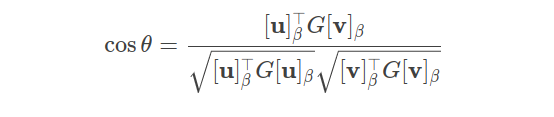
举例说明
设定:
地球人:标准正交基,点P的坐标(3,4).
外星人:非正交基,从地球人的角度看,其基坐标为:
但是对于外星人来说,他们同样认为自己的基是(1,0)和(0,1),和地球人无异。地球人根据基变换规则,计算出同样的P点在外星人的坐标系下的坐标为:

地球人计算P点到原点的坐标,根据勾股定理:
在小尺度下,外星人没有意识到自己使用的基是非正交的,如果其同样知道了勾股定理,则其计算两点间距离的方式和地球人一样,根据勾股定理:
同样空间中两点间的距离,外星人计算出的结果和地球人不同!
两个文明之间开始意识到哪里出了问题。
问题解决
矛盾出现后,双方可能通过以下方式发现坐标系差异,交换基的信息,地球人立刻就会发现外星人使用的基不是正交的。外星人意识到这一点后,立刻根据自己的基向量在地球人的标准坐标系下的坐标,计算出度规矩阵G:
外星人根据度规矩阵重新计算向量内积得到距离,应用内积公式:
进而得到和地球人同样的P点距离原点的距离值是5,两个文明最终就距离问题达成了一致。这里面的关键在于认识到度量矩阵G的存在。
总结
宇宙没有义务满足人类对直角的审美,正交性和平直性只是空间的局部近似,即使空间在大尺度上是弯曲的,但是对于活动范围有限的生命体来说,其认识到的空间是"局部可微“的,可以近似看成是平直的欧式空间,所以发展欧式几何来度量这个空间是文明自然而然的选择,生命并不能天然的觉察到自己所在的空间是弯曲的(可能生活在黑洞或者中子星附近的文明能够直观感受到非正交坐标系和非平直空间),除非像前面的例子一样,遇到不同文明的碰撞,或者产生出像爱因斯坦那样的天才,对人类的空间观念进行彻底的革新。
有限尺度生命体必然首先发展欧氏几何,因其与局域测量一致,内部突破需爱因斯坦式天才,将思想实验与数学重构结合,或者外部文明的输入。实际上,人类是通过自我突破完成上述认知的,人类已经发现我们地球所在的宇宙空间,其度规矩阵G并非单位矩阵,这实际上说明,我们人类才是例子中的那个外星文明。
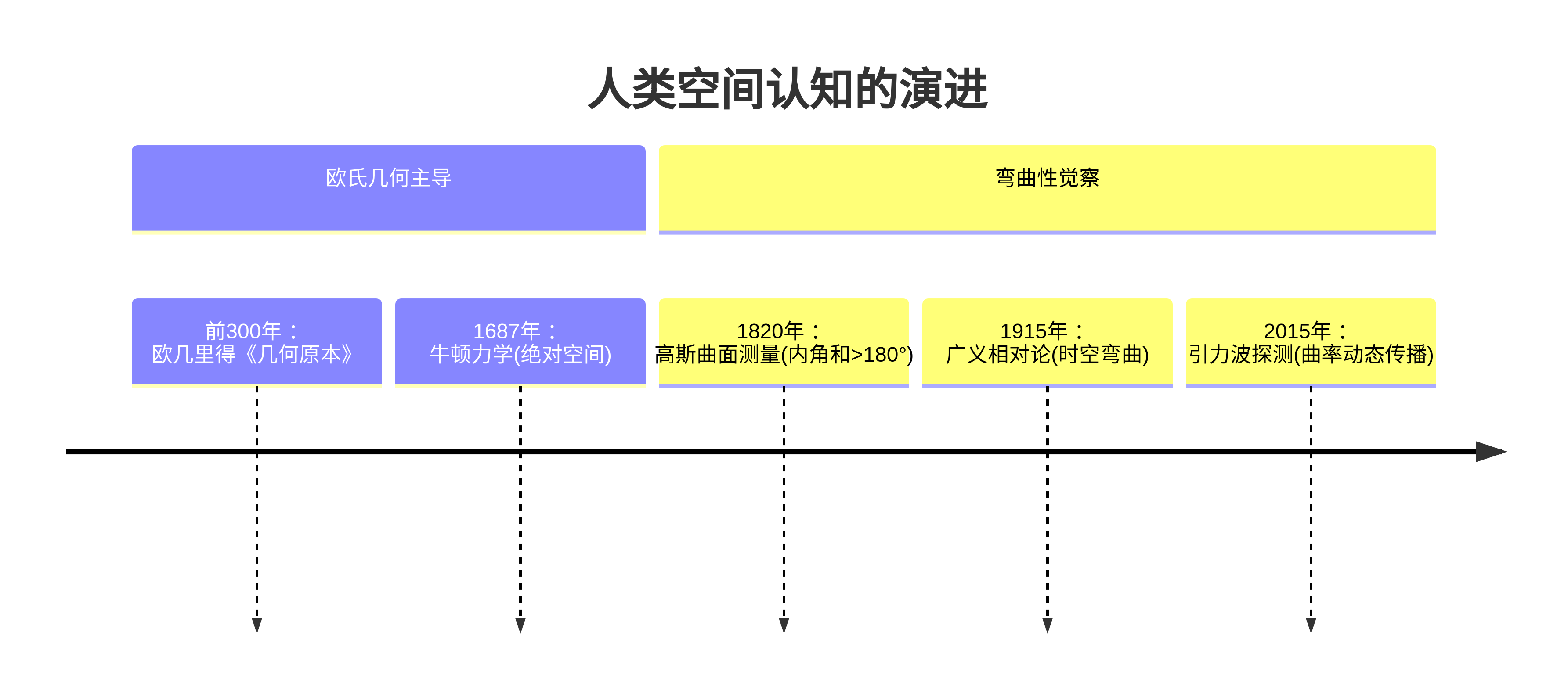
这印证了,从局部欧氏到全局弯曲的认知跃迁,需千年量级的科学积累。
