01数据结构-关键路径

前言

我们在写拓扑排序的时候提到，拓扑排序是关键路径的基础，那么为什么这么说呢？在此之前我们看一些简单但很重要的概念。

1.基础概念

• 什么是AOE网？

  AOE网（Activity On Edge）即边表示活动的网，是与AOV网（顶点表示活动）相对应的一个概念。而拓扑排序恰恰就是在AOV网上进行的，这是拓扑排序与关键路径最直观的联系。AOE网是一个带权的有向无环图，其中顶点表示事件（Event），弧表示活动，权表示活动持续的时间。下面的就是一个AOV网：
  
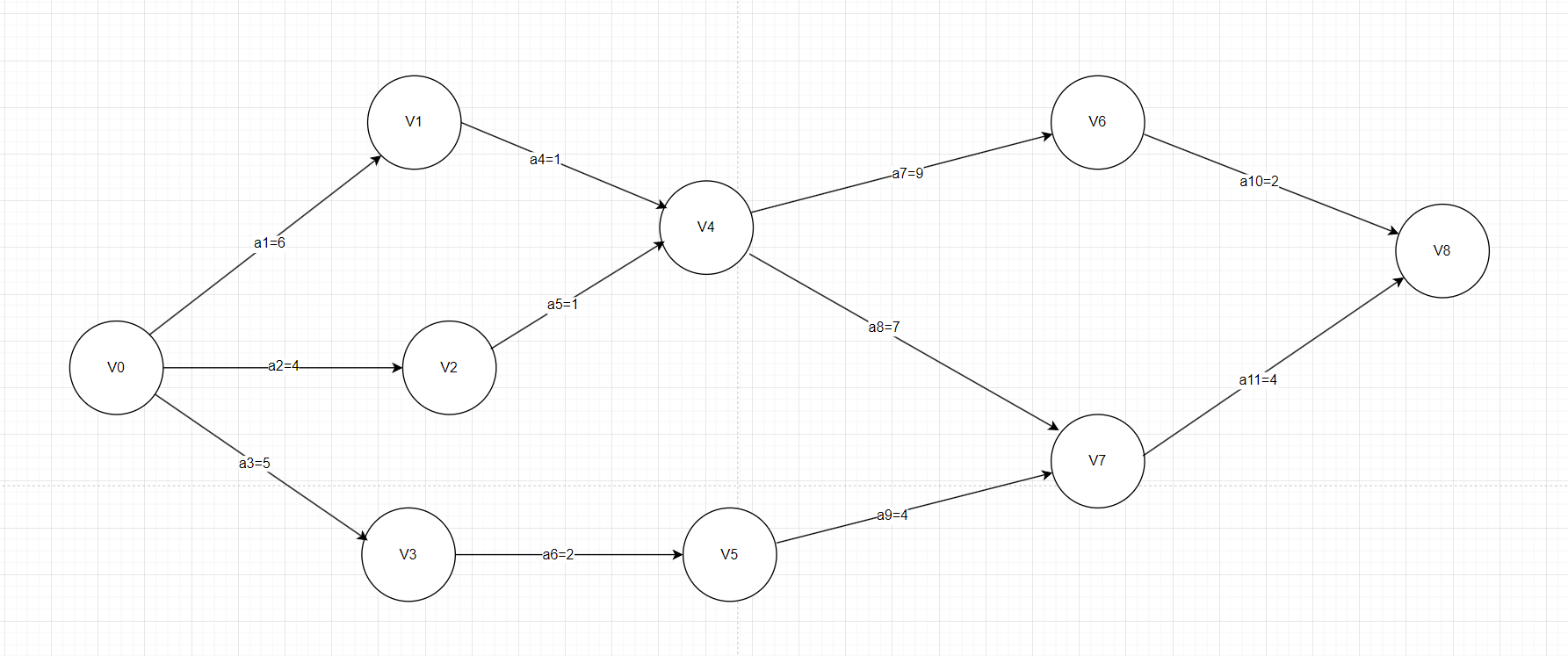
  图1

  其中V0，V2，V3…V8表示事件，a1…a11表示活动，活动的取值表示完成该活动所需要的时间，如a1 = 6表示完成活动a1所需要的时间为6天。此外，每一事件Vi表示在它之前的活动已经完成，在它之后的活动可以开始，如V4表示活动a4和a5已经完成，活动a7和a8可以开始了。

• AOE网的源点和汇点？

  由于一个工程中只有一个开始点和一个完成点，故将AOE网中入度为零的点称为源点，将出度为零的点称为汇点。

  打个比方，我们现在有一个工程，就是将大象装进冰箱，那么源点就相当于我们现在接到这样一个任务，而汇点则表示我们完成了这个任务。那么我们之前所讲的打开冰箱⻔，将大象装进去，关上冰箱⻔就属于活动本身（即a1…a11所表示的信息），打开冰箱⻔所需要的时间就是活动所需要的时间，而完成某一个活动所到达的顶点就表示一个事件（冰箱⻔打开）。上图中的顶点V0表示源点， V8表示汇点。

• 什么是关键路径？

  举个非常形象的栗子。
  唐僧师徒从⻓安出发去⻄天取经，佛祖规定只有四人一起到达⻄天方能取得真经。假如师徒四人分别从⻓安出发，走不同的路去⻄天：孙悟空一个筋斗云十万八千里，一盏茶的功夫就到了；八戒和沙和尚稍慢点也就一天左右的时间；而唐僧最慢需要14年左右。徒弟到达后是要等着师傅的。那么用时最⻓的唐僧所走的路，就是取经任务中的关键路径。其他人走的路径属于非关键路径。

  由于AOE网中的有些活动是可以并行进行的（如活动a1、a2和a3就是可以并行进行的），所以完成工程的最短时间是从源点到汇点的最⻓路径的⻓度。路径⻓度最⻓的路径就叫做 关键路径（Critical Path）。如下图2中红色顶点和有向边构成的就是一条关键路径，关键路径的⻓度就是完成活动 a1、a4和a9、a10所需要的时间总和，即为 6+1+9+2 = 18。
  
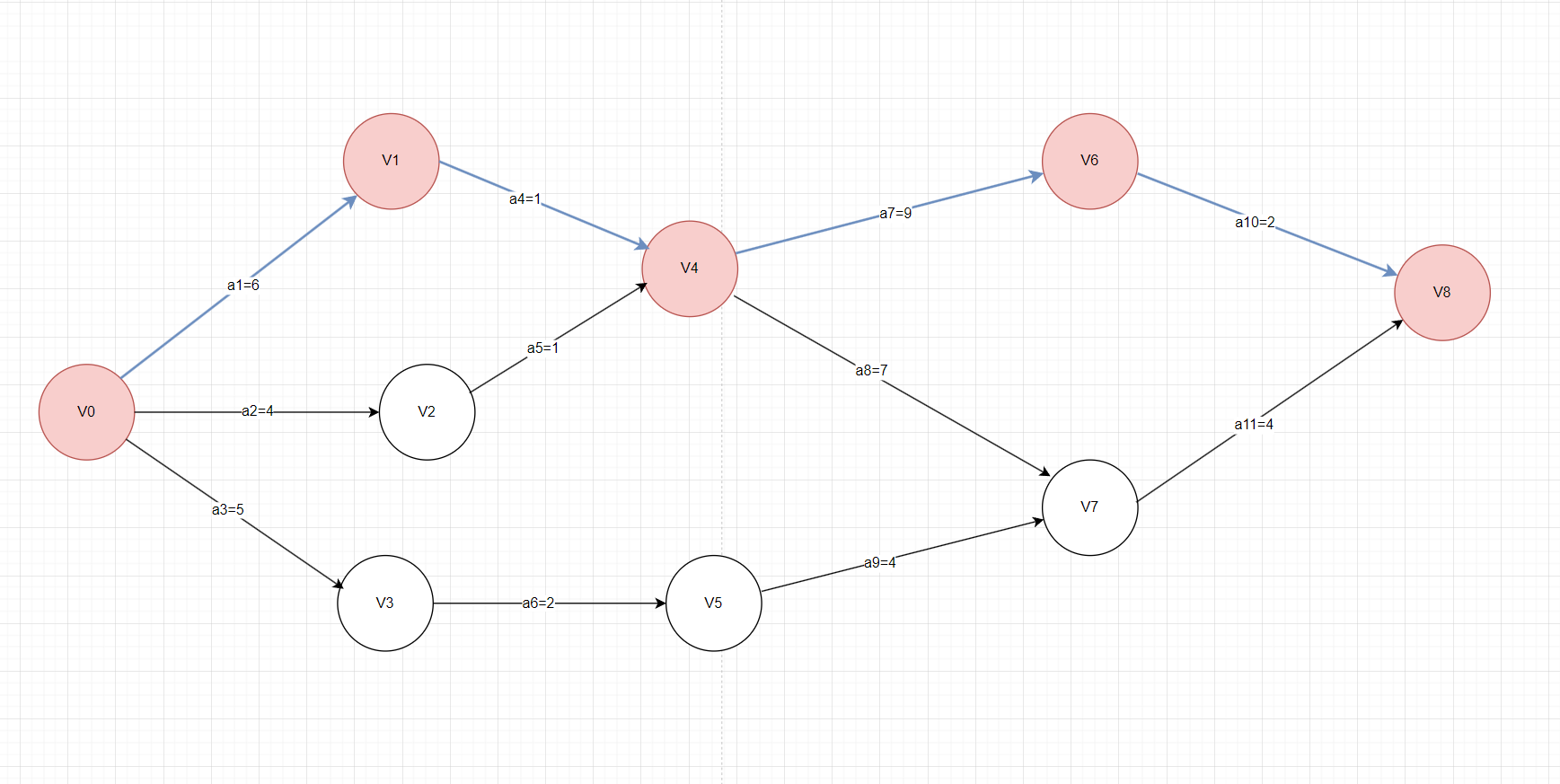
  图2

• 什么是ETV？

  ETV（Earliest Time Of Vertex)：事件最早发生时间，就是顶点的最早发生时间；(看图说话)
  

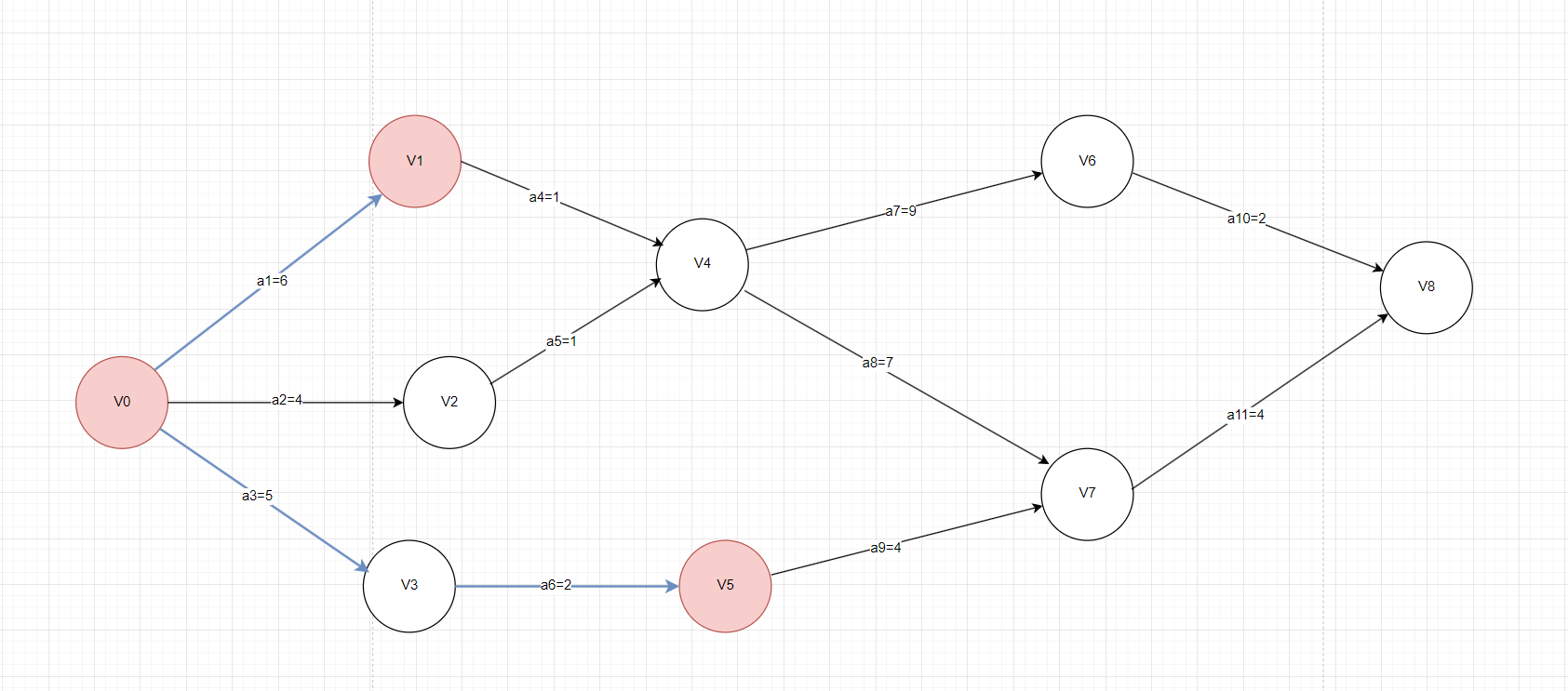
图3

事件V1的最早发生时间表示从源点V0出发到达顶点V1经过的路径上的权值之和，从源点V0出发到达顶点V1只经过了权值为6的边，则V1的最早发生时间为6，表示在活动a1完成之后，事件V1才可以开始；同理，事件V5要发生（即最早发生）需要活动a3和活动a6完成之后才可以，故事件V5的最早发生时间为 5 + 2 = 7。其他顶点（事件）的最早发生时间同理可的。需要说明，事件的最早发生时间一定是从源点到该顶点进行计算的

• 什么是LTV？

  LTV（Latest Time Of Vertex)：事件最晚发生时间，就是每个顶点对应的事件最晚需要开始的时间，如果超出此时间将会延误整个工期。
  
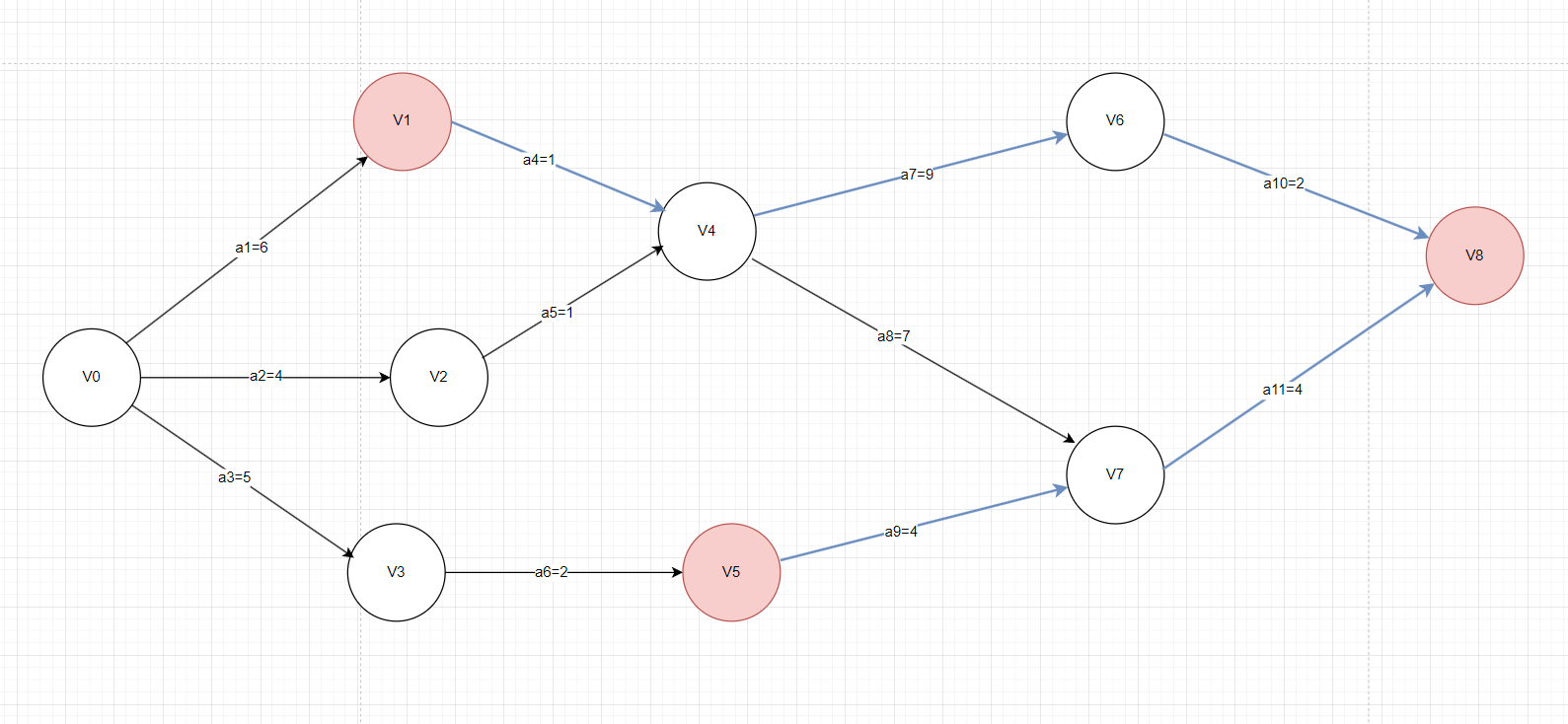
  图4

  前面在谈关键路径的概念时给出了一条上图中的关键路径，该关键路径（ V0，V1，V4 ，V6，V8）的⻓度为18，为什么要提这个⻓度呢，因为要计算某一个事件的最晚发生时间，我们需要从汇点V8进行倒推。计算顶点V2的最晚发生时间为例，已知关键路径的⻓度为18，事件V1到汇点V8所需要的时间为 1 + 9 + 2 = 12，则事件V1的最晚发生时间为18-12 = 6，这时候我们发现，这和事件V2的最早发生时间不是一样吗？的确如此，对于关键路径上的顶点都满足最早发生时间 etv 等于 最晚发生时间 ltv 的情况，这也是我们识别关键活动的关键所在再来计算一下事件V5的最晚发生时间，事件V5到汇点V8所需要的时间为 4 + 4 = 8，则事件V5的最晚发生时间为 18 - 8 = 10；相当于说活动a6完成之后，大可以休息 2天，再去完成活动a9也不会影响整个工期。

• 什么是ETE？

  ETE(Earliest Time Of Edge)：活动的最早开工时间，就是弧的最早发生时间。
  

  活动a4要最早开工时间为事件V1的最早发生时间 6；同理，活动a9的最早开工时间为事件v5的最早发生时间 7。显然活动的最早开工时间就是活动发生前的事件的最早开始时间。

• 什么是LTE?

  LTE(Lastest Time of Edge)：活动的最晚开工时间，就是不推迟工期的最晚开工时间。
  
  图5

  活动的最晚开工时间则是基于事件的最晚发生时间。比如活动a4的最晚开工时间为事件V4的最晚发生时间减去完成活动a4所需时间，即 7 - 1 = 6；活动 a9的最晚开工时间为事件V7的最晚发生时间减去完成活动a9所需时间，即 14 - 4 = 10；

  从上面也就可以看出 只要知道了每一个事件（顶点）的ETV 和 LTV，就可以推断出对应的 ETE 和 LTE . 此外还需要注意，关键路径是活动的集合，而不是事件的集合，所以当我们求得 ETV 和 LTV 之后，还需要计算 ETE 和 LTE 。

2.关键路径

2.1关键路径算法模拟

如图6，我们在事件最早发生的时间中，如果某个事件有多个入度，要选择路径权值和最大的那条，这和我们平时理解的最早发生不一样，因为在AOE网中，事件触发的条件性​​：一个事件的发生需其所有前置活动（指向该事件的边）均完成。先到的必须等后到的，例如：事件C由路径A（3天）和路径B（5天）指向，即使路径A先完成，仍需等待路径B结束，因此事件C的最早发生时间为5天。在计算事件最早发生的时间时要从源点V0出发到达其他顶点经过的路径上的权值之和(正推)。

在计算事件最晚发生的事件时，我们需要从汇点终点进行倒推。

注意ETV和LTV中对应活动的值相等时即为关键路径中的顶点(V0,V1,V4,V6,V7,V8)

图6

如图7，计算活动最早发生的时间就是这个活动连接的弧尾的最早发生时间，因为一个事件发生后活动才能执行，例如要计算a1,a2,a3的最早发生时间，就要找对应的边的弧尾的ETV，发现V0是0，所以a1,a2,a3的最早发生时间是0

活动的最晚开工时间则是基于事件的最晚发生时间，例如活动a4的最晚开工时间为事件V4的最晚发生时间减去完成活动a4所需时间，即 7 - 1 = 6

注意ETE和LTE中对应活动的值相等时即为关键路径中的边(a1,a4,a7,a8,a10,a11)

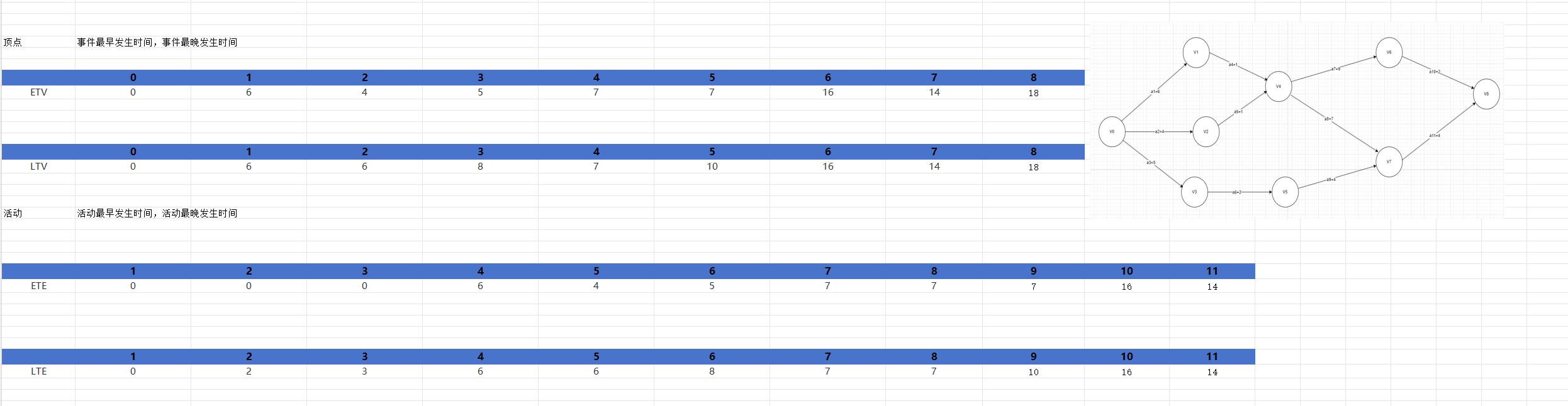
图7

2.2关键路径代码实现

路径实现接口:void keyPath(const AGraph *graph)

static void showTable(int *table, int n, const char *name) {printf("%s", name);for (int i = 0; i < n; ++i) {printf(" %d", table[i]);}printf("\n");
}void keyPath(const AGraph *graph) {// 1. 计算顶点的ETV和LTVint *ETV=malloc(sizeof(int)*graph->nodeNum);if (ETV==NULL) {return ;}int *LTV=malloc(sizeof(int)*graph->nodeNum);if (LTV==NULL) {return ;}memset(ETV, 0, sizeof(int) * graph->nodeNum);memset(LTV, 0, sizeof(int) * graph->nodeNum);topologicalOrder(graph,ETV,LTV);showTable(ETV, graph->nodeNum, "ETV: ");showTable(LTV, graph->nodeNum, "LTV: ");// 2. 计算边的ETE和LTE，直接输出关键路径for (int i = 0; i < graph->nodeNum; ++i) {// 每个边的最早发生时间就是边的弧尾的ETV// 每个边的最晚发生时间就是边的弧头的LTV减去当前边的权重值ArcEdge *edge=graph->nodes[i].firstEdge;while(edge) {if (ETV[i]==LTV[edge->no]-edge->weight) {printf("<%s> ---%d--- <%s>\n",graph->nodes[i].show, edge->weight, graph->nodes[edge->no].show);}edge = edge->next;}}free(ETV);free(LTV);
}

我们需要申请ETV和LTV两个空间，并把ETV和LTV初始化好，判断如果两个ETE和LTE对应相等的话，说明是关键路径，我们把初始化ETV和LTV封装成内在接口

初始化ETV和LTV：static int topologicalOrder(const AGraph *grap, int *ETV, int *LTV);

static int topologicalOrder(const AGraph *grap, int *ETV, int *LTV) {int *inDegree = malloc(sizeof(int) * grap->nodeNum);		// 入度记录表if (inDegree == NULL) {return -1;}memset(inDegree, 0, sizeof(int) * grap->nodeNum);// 1. 初始化图中所有顶点的入度记录表for (int i = 0; i < grap->nodeNum; i++) {if (grap->nodes[i].firstEdge) {ArcEdge *edge = grap->nodes[i].firstEdge;while (edge) {++inDegree[edge->no];edge = edge->next;}}}// 2. 将入度为0的节点入栈，出栈的时候int top = -1;int *stack = malloc(sizeof(int) * grap->nodeNum);int *topOut = malloc(sizeof(int) * grap->nodeNum);  //反算出LTV// 2.1 将初始化的入度为0的顶点编号压入栈，此点就是源点for (int i = 0; i < grap->nodeNum; ++i) {if (inDegree[i] == 0) {stack[++top] = i;break;				// 关键路径默认只有一个源点}}// 2.2 不断地弹栈，更新入度记录表int tmp = 0;			// 从栈上弹出的顶点编号int index = 0;			// 记录排序结果的情况while (top != -1) {tmp = stack[top--];topOut[index++] = tmp;ArcEdge *edge = grap->nodes[tmp].firstEdge;while (edge) {--inDegree[edge->no];if (inDegree[edge->no] == 0) {stack[++top] = edge->no;}if (ETV[tmp] + edge->weight > ETV[edge->no]) {ETV[edge->no] = ETV[tmp] + edge->weight;}edge = edge->next;}}free(inDegree);free(stack);if (index < grap->nodeNum) {		// 有环free(topOut);return -1;}tmp = topOut[--index];// 3. 更新LTVfor (int i = 0; i < grap->nodeNum; ++i) {LTV[i] = ETV[tmp];}while (index) {int getTopNo = topOut[--index];ArcEdge *edge = grap->nodes[getTopNo].firstEdge;while (edge) {if (LTV[edge->no] - edge->weight < LTV[getTopNo]) {LTV[getTopNo] = LTV[edge->no] - edge->weight;}edge = edge->next;}}free(topOut);return 0;
}

​​在本节课开始前为什么说拓扑排序是关键路径的基础呢？拓扑排序为关键路径计算提供顺序基础​​关键路径需按“最早开始时间（ETV）→ 最晚开始时间（LTV）”的顺序计算，而拓扑排序的结果直接提供了这种顺序。计算ETV时需从起点开始，按拓扑顺序依次处理顶点，确保前置活动的ETV已确定；计算LTV时需从终点逆序处理，同样依赖拓扑顺序。

由于我们计算LTV，而计算LTV 时需要从后往前开始算，所以我们需要定义两个栈，一个栈stack用来作为处理ETV时的缓冲区，用拓扑排序的思想拍好序，每从stack里弹出一个顶点，把这个顶点压入计算LTV的缓存区并做判断：这个顶点(弧尾)的ETV加上这条边的权重值是否大于弧头的ETV，若大于则更新弧头的ETV。直到stack为空，说明更新完毕ETV。

开始更新LTV，由于我们是倒过来计算各个事件的LTV的，所以我们需要先拿到缓存区的最后一个元素，所以先 tmp = topOut[--index];初始化LTV所有的值为拿到的这个栈顶事件的ETV，然后开始更新LTV。由于我们把index设为的是0，我们需要拿到弧尾的事件，所以现在循环中–拿到第一个我们要更新的元素，判断如果边的弧头的LTV减去当前边的权重值小于了弧尾的LTV，则把小的赋值给LTV。例如我们要求V7的LTV，初始时栈顶元素是V8,拿到V8，并把V8的ETV赋给LTV数组里的所有值，进入循环，由于V8已经弹栈，拿到V7(弧尾)，LTV[edge->no] - edge->weight < LTV[getTopNo]这个语句里面的边就是以V7为弧尾，V8为弧头的边，V8的LTV减去这条边的权值小于了V7的LTV，则把小的赋值给V7的LTV，计算的V8的LTV减去这条边的权值为18-4==11<V7的LTV(18)。更新为14，符合我们在2.1关键路径算法模拟中分析的到的结果。

最后来测一下:

#include <stdio.h>
#include <stdlib.h>
#include "keyPath.h"AGraph *setupAGrap() {char *names[] = {"V0", "V1", "V2", "V3","V4", "V5", "V6", "V7","V8"};int n = sizeof(names)/sizeof(names[0]);AGraph *grap = createAGraph(n);if (grap == NULL) {return NULL;}initAGraph(grap, names, n, 1);addAGraph(grap, 0, 1, 6);addAGraph(grap, 0, 2, 4);addAGraph(grap, 0, 3, 5);addAGraph(grap, 1, 4, 1);addAGraph(grap, 2, 4, 1);addAGraph(grap, 3, 5, 2);addAGraph(grap, 4, 6, 9);addAGraph(grap, 4, 7, 7);addAGraph(grap, 5, 7, 4);addAGraph(grap, 6, 8, 2);addAGraph(grap, 7, 8, 4);return grap;
}int main() {AGraph *graph = setupAGrap();if (graph == NULL) {return -1;}keyPath(graph);return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\03_GraphStruct\KeyPath.exe
ETV:  0 6 4 5 7 7 16 14 18
LTV:  0 6 6 8 7 10 16 14 18
<V0> ---6--- <V1>
<V1> ---1--- <V4>
<V4> ---7--- <V7>
<V4> ---9--- <V6>
<V6> ---2--- <V8>
<V7> ---4--- <V8>进程已结束，退出代码为 0

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。