PID控制算法

引言

在工业领域上，精准性和稳定性是非常重要的，人工的实时调节不能够完全胜任高精度和高稳定性的工作，于是用数学手段替代人工经验，自动校正系统误差（设定值与实际值的偏差）。

一、基本原理

1.1.简介

PID（比例-积分-微分）控制器是一种广泛应用于工业控制系统的反馈控制算法，PID 是一种闭环控制算法，它动态改变施加到被控对象的输出值（Out），使得被控对象某一物理量的实际值（Actual），能够快速、准确、稳定地跟踪到指定的目标值（Target）。PID 是一种基于误差（Error）调控的算法，其中规定：误差=目标值-实际值，PID 的任务是使误差始终为 0，对被控对象模型要求低，无需建模，即使被控对象内部运作规律不明确，PID 也能进行调控。PID 就像驾驶汽车时：

• P：眼睛看到偏离车道，立即打方向盘修正（现在）
• I：如果持续偏离，逐渐加大修正力度（过去）
• D：预判车辆趋势，提前减速或减速防止过度转向（未来）

1.2.开环与闭环

• 开环（Open Loop）：控制器单向输出值给被控对象，不获取被控对象的反馈，控制器对被控对象的执行状态不清楚

• 闭环（Closed Loop）：控制器输出值给被控对象，同时获取被控对象的反馈，控制器知道被控对象的执行状态，可以根据反馈修改输出值以优化控制

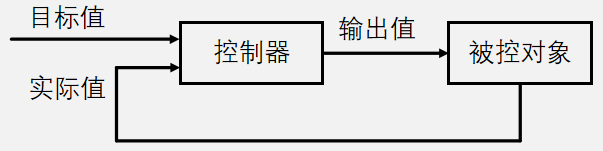
1.3.PID 的公式

• 定义误差：

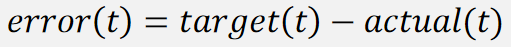
• PID输出值：

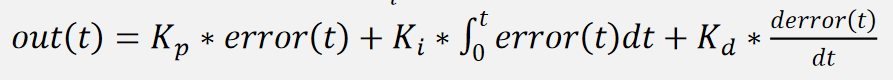
下图是 PID 闭环控制图，首先，用户输入目标值给被控对象并通过被控对象反馈出来的实际值算出误差，基于本次误差和历史误差算出输出值给被控对象，实现实际值跟踪目标值：

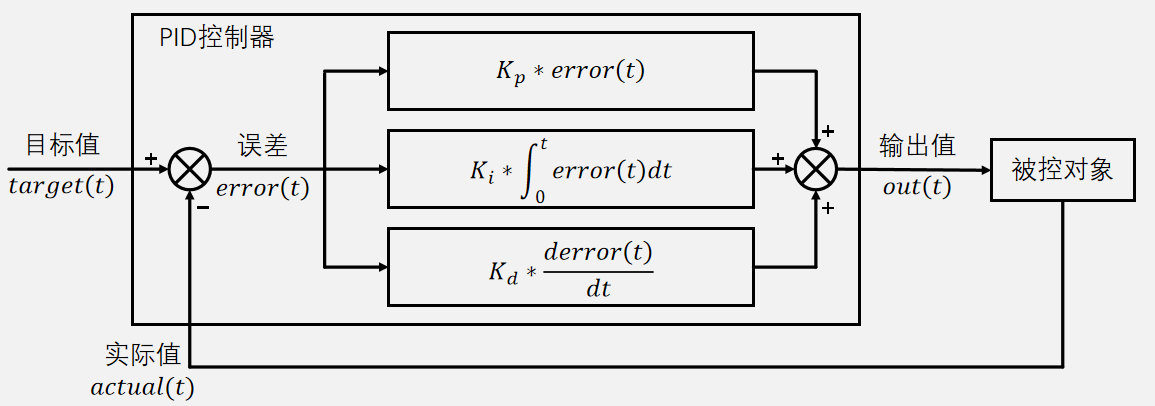
1.3.1.比例项（Proportional）

比例项的输出值仅取决于当前时刻的误差，与历史时刻无关。当前存在误差时，比例项输出一个与误差呈正比的值，当前不存在误差时，比例项输出 0，下面式子是只含有比例项的 PID 输出值：

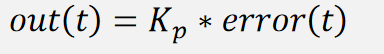
Kp 越大，比例项权重越大，系统响应越快，但超调也会随之增加，如下图红框所示：

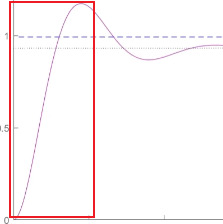
如果只是纯比例项控制，系统一般会存在稳态误差，Kp 越大，稳态误差越小，实际值与目标值存在恒定偏差，即稳态误差。产生稳态误差的原因：纯比例项控制时，若误差为 0，则比例项结果也为 0。被控对象输入 0 时，一般会自发地向一个方向偏移，产生误差。产生误差后，误差非 0，比例项负反馈调控输出，当调控输出力度和自发偏移力度相同时，系统达到稳态.

1.3.2.积分项（Integral）

积分项的输出值取决于 0 ~ t 所有时刻误差的积分，与历史时刻有关。积分项将历史所有时刻的误差累积，乘上积分项系数 Ki 后作为积分项输出值，用于弥补纯比例项产生的稳态误差，若系统持续产生误差，则积分项会不断累积误差，直到控制器产生动作，让稳态误差消失。下面是含有比例项和积分项的 PID 输出值：

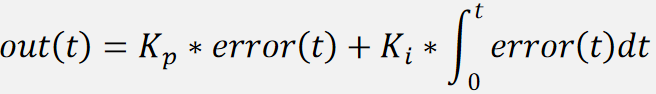
Ki 越大，积分项权重越大，稳态误差消失越快，但系统滞后性也会随之增加，如下图的红框所示：

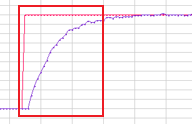
滞后性是实际值靠近目标值的增长速度慢，这样的现象会导致一些需要高平衡性的项目，带来较大的影响。

1.3.3.微分项（Differential）

微分项的输出值取决于当前时刻误差变化的斜率，与当前时刻附近误差变化的趋势有关。当误差急剧变化时，微分项会负反馈输出相反的作用力，阻碍误差急剧变化，斜率一定程度上反映了误差未来的变化趋势，这使得微分项具有 “预测未来，提前调控”的特性。微分项给系统增加阻尼，可以有效防止系统超调，尤其是惯性比较大的系统，下面式子是含有比例项、积分项和微分项的 PID 输出值：

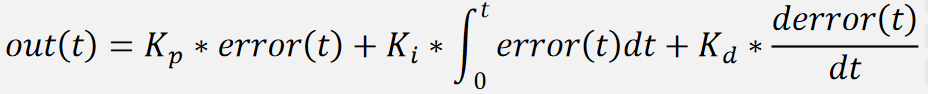
Kd 越大，微分项权重越大，系统阻尼越大，但系统卡顿现象也会随之增加，如果微分项过大，就会导致比例项和积分项让被控对象启动，微分项却阻止它们。

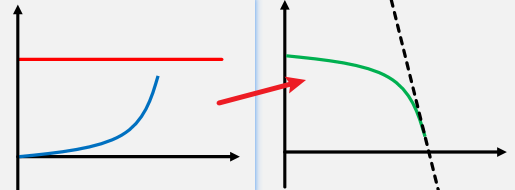
上图的红线是目标值，蓝线是实际值，绿线是输出值，当实际值斜率很大的时候，说明变化速度很快，输出值就要反向输出，让实际值的速度减缓。

1.4.连续形式与离散形式的 PID 公式

1.4.1.连续形式

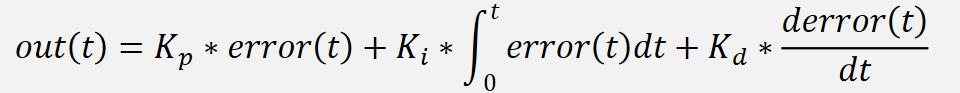
为了更好的在程序上实现 PID 式子，将积分符号和求导，变成简单的加、减、乘、除形式，因此该式子变为离散形式。

1.4.2.离散形式

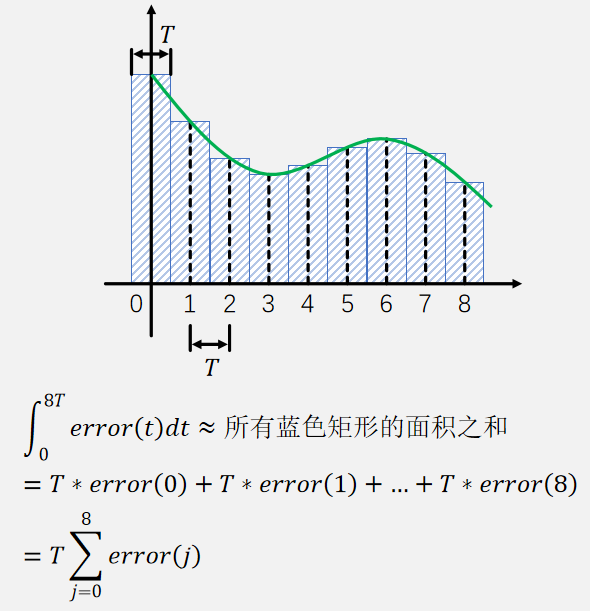
比例项不变，积分项原本的意思就是从 0 时刻开始到 t 时刻的误差之和，离散之后就是相当于求曲线下面的面积，如下图所示：每个调控周期为 T，一共有 8 个 T，每个时刻的误差乘以调控周期 T，最后相加。j 是相当于 for 循环里面的变量 i，用于遍历。

微分项就是在某点求导，离散之后，就是求当前时刻和上一个时刻连线的斜率，如下图的红线，求 5T 时刻的斜率，离散之后还需知道上一次的 4T 时的误差，两点相减之后再除以调控周期 T 即可求得：

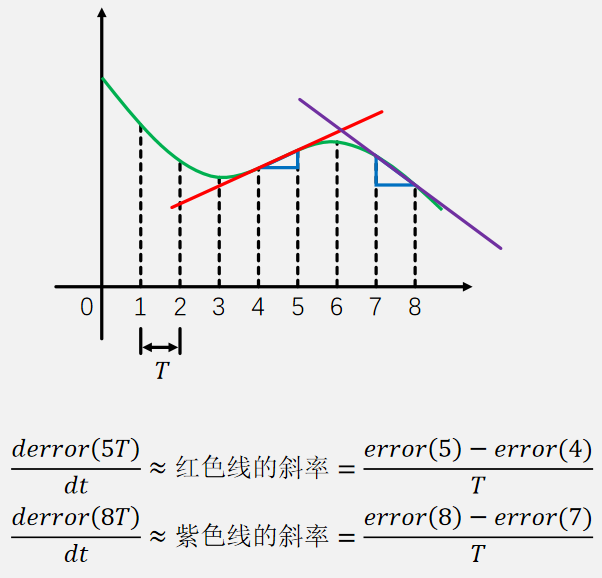
经过以上变化，得出离散的 PID 式子：

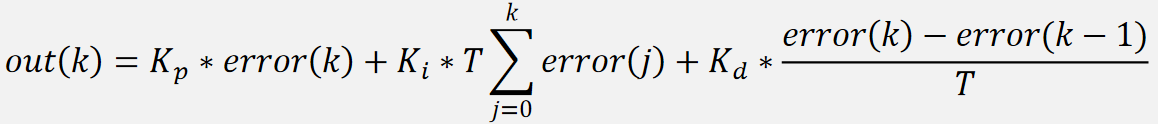
上面式子需要考虑调控周期 T，如果将调控周期 T 直接并入 Ki 和 Kd，即可获得下面式子：

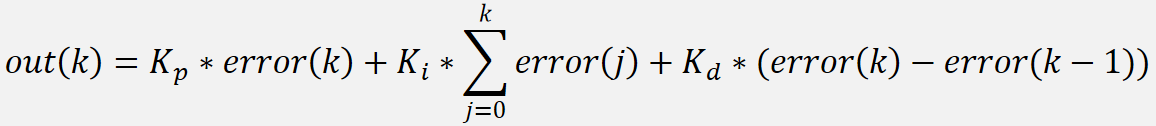
该式子只需考虑当前误差（error(k)），历史误差（error(j)），上一个误差（error(k-1)）三个误差，其中 Kp、Ki 和 Kd 由用户自己设置。

1.5.位置式 PID 与增量式 PID

1.5.1.位置式

位置式 PID 由连续形式 PID 直接离散得到，每次计算得到的是全量的输出值，可以直接给被控对象，例如，阀门控制项目，位置式 PID 每次都会反馈完整的阀门状态。

1.5.2.增量式

增量式 PID 由位置式 PID 推导得到，每次计算得到的是输出值的增量，如果直接给被控对象，则需要被控对象内部有积分功能；增量式 PID 也可在控制器内进行积分，然后输出积分后的结果，此时增量式 PID 与位置式 PID 整体功能没有区别，下面是增量式 PID 的推导：

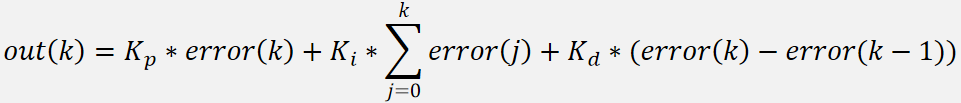
当 k = k - 1，再让 out(k) - out(k-1)，得到增量式，增量式需要用到当前时刻的误差、上一次的误差和上上次的误差：

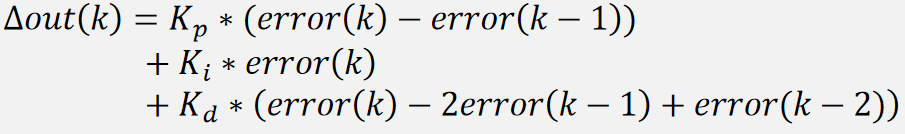
1.6.程序实现

先确定一个调控周期 T，本次实验选择软件定时器设置中断，每中断 一次就是一次调控周期，这样设计，主函数能够运行更多的代码，提高了 CPU 利用率，下面是大致代码实现：

int main(void)
{Timer_Init();while(1){}
}void TIM2_IRQHandler(void)
{if(TIM_GetITStatus(TIM2, TIM_IT_Update) == SET){//每隔时间T，程序执行到该中断服务函数//在该中断服务函数里执行PID调控TIM_ClearITPendingBit(TIM2, TIM_IT_Update);}
}

• 位置式

float Target, Actual, Out;			//目标值、实际值、输出值
float Kp = 值, Ki = 值, Kd = 值;	//比例项、积分项、微分项
float Error0, Error1, ErrorInt;		//本次误差、上次误差、误差积分int main(void)
{Timer_Init();while(1){//用户在此处根据需求写入PID控制器的目标值Target = 值;}
}void TIM2_IRQHandler(void)
{if(TIM_GetITStatus(TIM2, TIM_IT_Update) == SET){//每隔时间T，程序执行到该中断服务函数//在该中断服务函数里执行PID调控//获取实际值Actual = 读取传感器();//获取本次误差和上次误差Error1 = Error0;Error0 = Target - Actual;//误差积分(累加)ErrorInt += Error0;//PID计算	Out = Kp * Error0 + Ki * ErrorInt + Kd * (Error0 - Error1);//输出限幅if(Out > 上限){Out = 上限;}if(Out < 下限){Out = 下限;}//执行控制输出至被控对象(Out);TIM_ClearITPendingBit(TIM2, TIM_IT_Update);}
}

• 增量式：增量式不需要积分累加，但是需要知道上上次的误差，该程序是在控制器内进行积分，也就是输出的 Out 值已经累加好的

float Target, Actual, Out;			//目标值、实际值、输出值
float Kp = 值, Ki = 值, Kd = 值;	//比例项、积分项、微分项
float Error0, Error1, Error2;		//本次误差、上次误差、上上次误差int main(void)
{Timer_Init();while(1){//用户在此处根据需求写入PID控制器的目标值Target = 值;}
}void TIM2_IRQHandler(void)
{if(TIM_GetITStatus(TIM2, TIM_IT_Update) == SET){//每隔时间T，程序执行到该中断服务函数//在该中断服务函数里执行PID调控//获取实际值Actual = 读取传感器();//获取本次误差、上次误差和上上次的误差Error2 = Error1;Error1 = Error0;Error0 = Target - Actual;//误差积分(累加)ErrorInt += Error0;//PID计算	Out = Kp * (Error0 - Error1) + Ki * Error0 + Kd * (Error0 - 2 * Error1 + Error2);//输出限幅if(Out > 上限){Out = 上限;}if(Out < 下限){Out = 下限;}//执行控制输出至被控对象(Out);TIM_ClearITPendingBit(TIM2, TIM_IT_Update);}
}

二、实验

2.1.位置式PID定速控制

实验目的：使用电位器旋钮修改 Kp、Ki、Kd 和 Target，修改 Kp、Ki、Kd 使得实际值尽量贴合目标值。下面是代码实现：

int main(void)
{/*模块初始化*/OLED_Init();		//OLED初始化Key_Init();			//非阻塞式按键初始化Motor_Init();		//电机初始化Encoder_Init();		//编码器初始化RP_Init();			//电位器旋钮初始化Serial_Init();		//串口初始化，波特率9600Timer_Init();		//定时器初始化，定时中断时间1ms/*OLED打印一个标题*/OLED_Printf(0, 0, OLED_8X16, "Speed Control");OLED_Update();while (1){/*电位器旋钮修改Kp、Ki、Kd和目标值*//*RP_GetValue函数返回电位器旋钮的AD值，范围：0~4095*//* 除4095.0可以把AD值归一化，再乘上一个系数，可以调整到一个合适的范围*/Kp = RP_GetValue(1) / 4095.0 * 2;				//修改Kp，调整范围：0~2Ki = RP_GetValue(2) / 4095.0 * 2;				//修改Ki，调整范围：0~2Kd = RP_GetValue(3) / 4095.0 * 2;				//修改Kd，调整范围：0~2Target = RP_GetValue(4) / 4095.0 * 300 - 150;	//修改目标值，调整范围：-150~150/*OLED显示*/OLED_Printf(0, 16, OLED_8X16, "Kp:%4.2f", Kp);			//显示KpOLED_Printf(0, 32, OLED_8X16, "Ki:%4.2f", Ki);			//显示KiOLED_Printf(0, 48, OLED_8X16, "Kd:%4.2f", Kd);			//显示KdOLED_Printf(64, 16, OLED_8X16, "Tar:%+04.0f", Target);	//显示目标值OLED_Printf(64, 32, OLED_8X16, "Act:%+04.0f", Actual);	//显示实际值OLED_Printf(64, 48, OLED_8X16, "Out:%+04.0f", Out);		//显示输出值OLED_Update();	//OLED更新，调用显示函数后必须调用此函数更新，否则显示的内容不会更新到OLED上Serial_Printf("%f,%f,%f\r\n", Target, Actual, Out);		//串口打印目标值、实际值和输出值//配合SerialPlot绘图软件，可以显示数据的波形}
}void TIM1_UP_IRQHandler(void)
{/*定义静态变量（默认初值为0，函数退出后保留值和存储空间）*/static uint16_t Count;		//用于计次分频if (TIM_GetITStatus(TIM1, TIM_IT_Update) == SET){/*每隔1ms，程序执行到这里一次*/Key_Tick();				//调用按键的Tick函数/*计次分频*/Count ++;				//计次自增if (Count >= 40)		//如果计次40次，则if成立，即if每隔40ms进一次{Count = 0;			//计次清零，便于下次计次/*获取实际速度值*//*Encoder_Get函数，可以获取两次读取编码器的计次值增量*//*此值正比于速度，所以可以表示速度，但它的单位并不是速度的标准单位*//*此处每隔40ms获取一次计次值增量，电机旋转一周的计次值增量约为408*//*因此如果想转换为标准单位，比如转/秒*//*则可将此句代码改成Actual = Encoder_Get() / 408.0 / 0.04;*/Actual = Encoder_Get();/*获取本次误差和上次误差*/Error1 = Error0;			//获取上次误差Error0 = Target - Actual;	//获取本次误差，目标值减实际值，即为误差值/*误差积分（累加）*//*如果Ki不为0，才进行误差积分，这样做的目的是便于调试*//*因为在调试时，我们可能先把Ki设置为0，这时积分项无作用，误差消除不了，误差积分会积累到很大的值*//*后续一旦Ki不为0，那么因为误差积分已经积累到很大的值了，这就导致积分项疯狂输出，不利于调试*/if (Ki != 0)				//如果Ki不为0{ErrorInt += Error0;		//进行误差积分}else						//否则{ErrorInt = 0;			//误差积分直接归0}/*PID计算*//*使用位置式PID公式，计算得到输出值*/Out = Kp * Error0 + Ki * ErrorInt + Kd * (Error0 - Error1);/*输出限幅*/if (Out > 100) {Out = 100;}		//限制输出值最大为100if (Out < -100) {Out = -100;}	//限制输出值最小为100/*执行控制*//*输出值给到电机PWM*//*因为此函数的输入范围是-100~100，所以上面输出限幅，需要给Out值限定在-100~100*/Motor_SetPWM(Out);}TIM_ClearITPendingBit(TIM1, TIM_IT_Update);}
}

2.2.增量式 PID 定速控制

本次实验和位置式定速控制的实验目的一样，下面是中断服务函数代码：

float Target, Actual, Out;			//目标值，实际值，输出值
float Kp, Ki, Kd;					//比例项，积分项，微分项的权重
float Error0, Error1, Error2;		//本次误差，上次误差，上上次误差void TIM1_UP_IRQHandler(void)
{/*定义静态变量（默认初值为0，函数退出后保留值和存储空间）*/static uint16_t Count;		//用于计次分频if (TIM_GetITStatus(TIM1, TIM_IT_Update) == SET){/*每隔1ms，程序执行到这里一次*/Key_Tick();				//调用按键的Tick函数/*计次分频*/Count ++;				//计次自增if (Count >= 40)		//如果计次40次，则if成立，即if每隔40ms进一次{Count = 0;			//计次清零，便于下次计次/*获取实际速度值*//*Encoder_Get函数，可以获取两次读取编码器的计次值增量*//*此值正比于速度，所以可以表示速度，但它的单位并不是速度的标准单位*//*此处每隔40ms获取一次计次值增量，电机旋转一周的计次值增量约为408*//*因此如果想转换为标准单位，比如转/秒*//*则可将此句代码改成Actual = Encoder_Get() / 408.0 / 0.04;*/Actual = Encoder_Get();/*获取本次误差、上次误差和上上次误差*/Error2 = Error1;			//获取上上次误差Error1 = Error0;			//获取上次误差Error0 = Target - Actual;	//获取本次误差，目标值减实际值，即为误差值/*PID计算*//*使用增量式PID公式，计算得到输出值*/Out += Kp * (Error0 - Error1) + Ki * Error0+ Kd * (Error0 - 2 * Error1 + Error2);/*输出限幅*/if (Out > 100) {Out = 100;}		//限制输出值最大为100if (Out < -100) {Out = -100;}	//限制输出值最小为100/*执行控制*//*输出值给到电机PWM*//*因为此函数的输入范围是-100~100，所以上面输出限幅，需要给Out值限定在-100~100*/Motor_SetPWM(Out);}TIM_ClearITPendingBit(TIM1, TIM_IT_Update);}
}

增量式的现象和位置式的现象看起来是一样的，但是在增量式的实验中，当 PID 三个值确定之后，设定一个目标值，再让实际值跟上目标值，最后把 PID 三个值调整为 0，这个时候还有输出值，是因为增量式在程序里式叠加的，如果 PID 三项都为 0，输出值还保留着上一次的输出值，只是不再有变化而已，如下图所示：

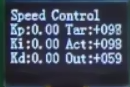
2.3.位置式 PID 定位置控制

实验目的：使用电位器旋钮修改 Kp、Ki、Kd 和 Target，使得实际值转动到目标值，本次实验代码与位置式定速控制实验代码一样，只在中断服务函数里面修改实际值 += 获取编码器速度，因为 += 就是积分表达，速度的积分就是位置。

Actual += Encoder_Get();

有下面图可以看出，纯比例项调节也可以做到尽可能贴合目标值了，绿色的输出线在实际值与目标值变化的时候才有波动，当实际值和目标值重合时输出值为 0。

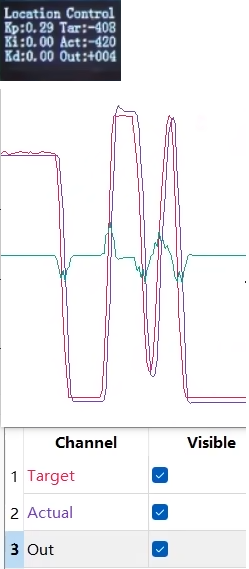
2.4.增量式 PID 定位置控制

实验目的：使用电位器旋钮修改 Kp、Ki、Kd 和 Target，使得实际值转动到目标值，本次实验代码与增量式定速控制实验代码一样，只在中断服务函数里面修改实际值 += 获取编码器速度。

Actual += Encoder_Get();

如果将 Ki 调到 0 并快速扭动改变目标值，就会出现实际值与目标值严重偏移的现象：

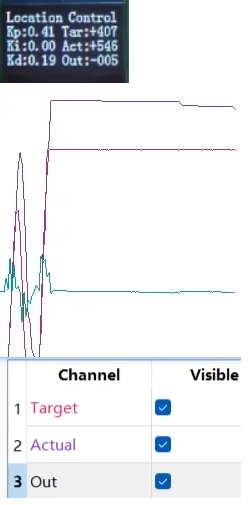
增量式定位置控制非常依赖这个积分项，没有积分项的增量式 PID，容易出现实际值和目标值偏移的问题，或者，如果上一次的输出值式错误的，同时后续的 Error 变化很小，则纯比例项调节很难纠正这个错误。此外，增量式的纯比例项调节，需要借助上一次的输出值，这使得即使是纯比例项调节，也会有一点积分项的特性，因此，增量式 PID 最好不要给 Ki 为 0。

三、算法改进

以下修改均在位置式 PID 定位置控制实验里。

3.1.积分限幅

要解决的问题：如果执行器因为卡住、断电、损坏等原因不能消除误差，则误差积分会无限制加大，进而达到深度饱和状态，此时 PID 控制器会持续输出最大的调控力，即使后续执行器恢复正常，PID 控制器在短时间内也会维持最大的调控力，直到误差积分从深度饱和状态退出。例如，用手指抵住正在旋转的转盘，过一段时间再放手，得到的波形如下图所示：

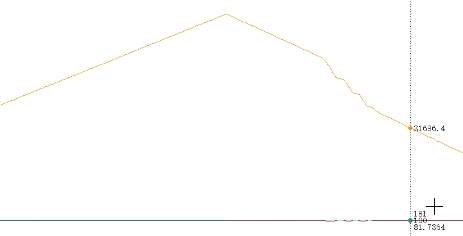
抵住的时间越久，积分项累积的输出值就越大，恢复到稳定输出值的时间就越久。积分限幅实现思路：对误差积分或积分项输出进行判断，如果幅值超过指定阈值，则进行限制，具体操作如下：

	/*误差积分（累加）*/ErrorInt += Error0;/*积分限幅*/if (ErrorInt > 500) {ErrorInt = 500;}		//限制误差积分最大为500if (ErrorInt < -500) {ErrorInt = -500;}		//限制误差积分最小为-500Out = Kp * Error0 + Ki * ErrorInt + Kd * (Error0 - Error1);

3.2.积分分离

积分项作用一般位于调控后期，用来消除持续的误差，调控前期一般误差较大且不需要积分项作用，如果此时仍然进行积分，则调控进行到后期时，积分项可能已经累积了过大的调控力，这会导致超调。如下图所示，定位置控制实验里，需要实际值尽可能贴近目标值，当目标值改变过快时，就会出现下面情况，积分项一开始正方向累计输出值过多，因此需要负方向输出抵消，拿实例来说明，转盘转动过快，出现转过目标位置的情况，因此需要往回转动回到目标位置。

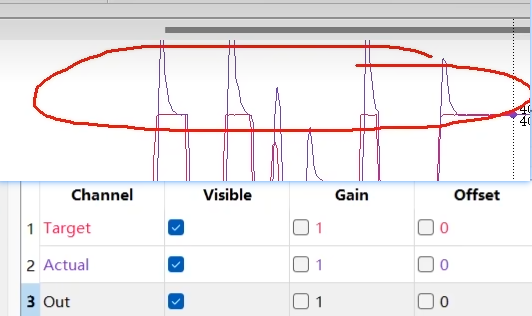
积分分离实现思路：对误差大小进行判断，如果误差绝对值小于指定阈值，则加入积分项作用，反之，则直接将误差积分清零或不加入积分项作用，下面实现积分分离，在获得本次误差和上次误差下面加上一下代码：

	/*误差积分+积分分离*/if (fabs(Error0) < 50)		//如果当前误差值小于指定的阈值{ErrorInt += Error0;		//才进行正常的误差积分}else						//否则，即当前误差值过大{ErrorInt = 0;			//此时不进行积分，同时把误差积分直接清零}Out = Kp * Error0 + Ki * ErrorInt + Kd * (Error0 - Error1);

阈值 50，是通过多次实验得出，如果超过阈值，积分项完全消失，就不会出现超过目标值的情况；如果阈值设定的太大，实验现象的效果不是很好。

3.3.变速积分

如果积分分离阈值没有设定好，被控对象正好在阈值之外停下来，则此时控制器完全没有积分作用，误差不能消除，如下图所示：

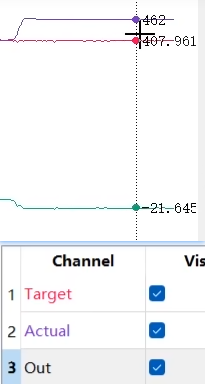
这时可以通过调大阈值的方法来解决，也可以通过变速积分来解决。变速积分简单来说只是在积分和不积分之间加了缓冲区，误差值越大，积分越弱，误差值越小，积分越强，如下图所示：

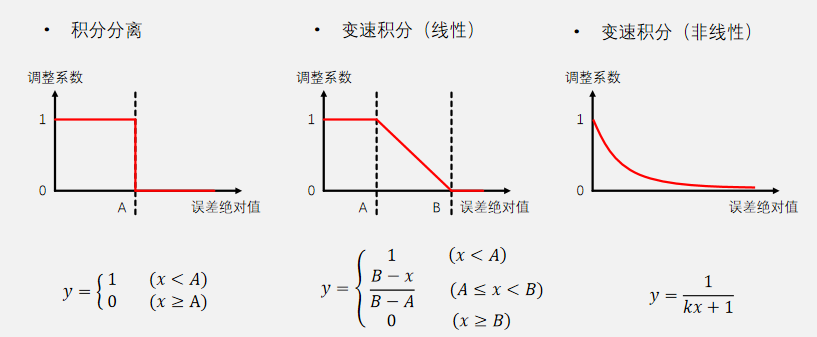
代码实现如下所示：

/*定义一个系数C，表示积分的速度，C的值与误差绝对值大小呈反比，误差绝对值越大，积分速度越慢*/float C = 1 / (0.2 * fabs(Error0) + 1);		//根据公式计算得到系数C/*误差积分*/ErrorInt += C * Error0;		//积分的速度由C确定，C的取值范围是0~1Out = Kp * Error0 + Ki * ErrorInt + Kd * (Error0 - Error1);

3.4.微分先行

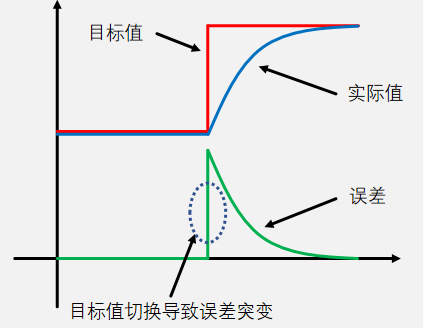
普通 PID 的微分项对误差进行微分，当目标值大幅度跳变时，误差也会瞬间大幅度跳变，这会导致微分项突然输出一个很大的调控力，如果系统的目标值频繁大幅度切换，则此时的微分项不利于系统稳定。微分项本来就是一个阻尼的作用，当 Kp、Ki 为 0 时，Kd 无论调成多少，按理来说都不会产生输出值，但是现实却是 Kp、Ki 为 0 时，也会有输出值，如下图所示：

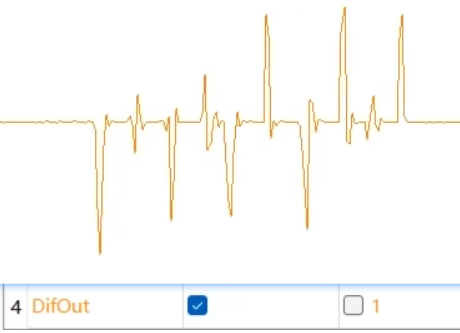
微分先行实现思路：将对误差的微分替换为对实际值的微分。下面是将微分项修改之后的式子：

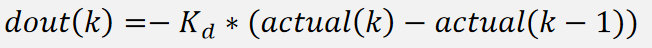
为什么需要加一个负号，因为是对实际值求微分，实际值在上升过程中需要一个反方向的输出才能平缓的到达目标值；而对误差求微分，误差逐渐变小的时候，斜率本来就是负的，因此对实际值求微分，需要添加一个负号。

下面是实现微分先行的代码：

	float DifOut, Actual1;				//定义一个微分项输出（方便查看波形），上次实际值Actual1 = Actual;			//获取上次实际值Actual += Encoder_Get();	//获取本次实际值/*获取本次误差和上次误差*/Error1 = Error0;			//获取上次误差Error0 = Target - Actual;	//获取本次误差，目标值减实际值，即为误差值/*PID计算，先得到微分项*/DifOut = - Kd * (Actual - Actual1);		//这一句是微分先行的微分项计算公式//计算结果要取负，因为实际值的变化趋势和误差变化趋势相反Out = Kp * Error0 + Ki * ErrorInt + DifOut;

3.5.不完全微分

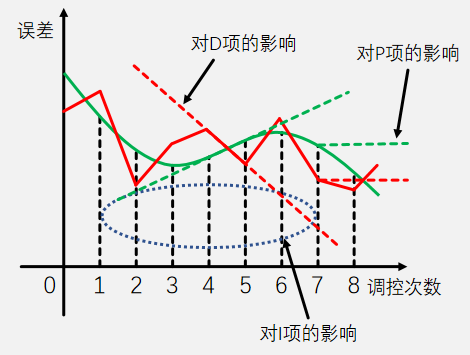
传感器获取的实际值经常会受到噪声干扰，而 PID 控制器中的微分项对噪声最为敏感，这些噪声干扰可能会导致微分项输出抖动，进而影响系统性能，如下图所示，下图是噪声对 PID 三项的影响：

• 对 P 项的影响：P 项只取决于当前误差，影响较小
• 对 I 项的影响：原本是绿色波形下面的面积，受到噪声的影响之后变成红色波形下面的面积了，但是 I 项面积有正负抵消的作用，影响也不是很大
• 对 D 项的影响：原本绿色的某一时刻的斜率是正的，受到噪声影响之后变成负的，因此受到噪声影响最大的是 D 项

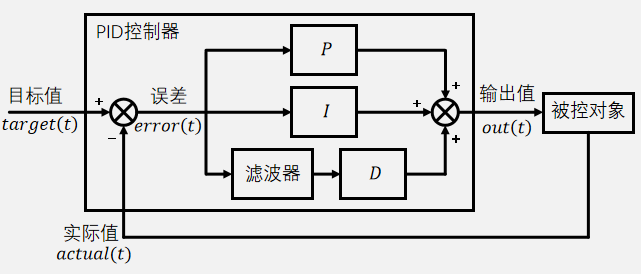
不完全微分实现思路：可以给 PID 三项都加上滤波器，这样会导致系统响应较慢，产生一定的滞后性；只给微分项加入一阶惯性单元（低通滤波器），这是对输出值反应速度较高的做法。如下图所示：

下面式子是不完全微分 PID 的微分项输出，上面的是算出当前的 D 项输出：

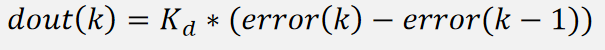
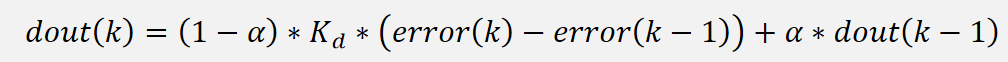
其中加号左边是本次的 D 项输入，右边是上一次的 D 项输出，由 a 来解决那一边的比重较高，该式子整体的意思是本次算的 D 项输入和上次输出的 dout 取平均值。

下面是代码实现：

	/*模拟给实际值添加一些噪声干扰*/Actual += rand() % 41 - 20;		//使用随机数生成函数rand生成随机数，并将结果限定在-20~20的范围内/*定义一个滤波强度系数a，a的取值范围是0~1，值越大表示滤波作用越强*/float a = 0.9;DifOut = (1 - a) * Kd * (Error0 - Error1) + a * DifOut;		//这一句是不完全微分的微分项计算公式Out = Kp * Error0 + Ki * ErrorInt + DifOut;

不完全微分的微分项计算公式中，等号左边是当前的微分项输出，右边的是上一次的微分项输出。

3.6.输出偏移

对于一些启动需要一定力度的执行器，若输出值较小，执行器可能完全无动作，这可能会引起调控误差，同时会降低系统响应速度。例如，启动一个电机，当 PWM 为 2% 时，无法使得电机转动，因此引起了调控误差，如下图所示：

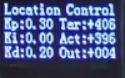
图中，目标值和实际值相差为 10，差值还是比较大的，可以用 Ki 来减小，但是当转盘停下来了，输出值还是不为 0，这是因为 P 项还有一点输出值来驱动转盘，但是这一点输出值不足以使得转盘转动。输出偏移实现思路：若输出值为0，则正常输出0，不进行调控；若输出值非0，则给输出值加一个固定偏移，跳过执行器无动作的阶段。下面是代码实现：

	/*输出偏移*/if (Out > 0)		//如果输出为正{Out += 6;		//则直接给输出值加上一个固定偏移}else if (Out < 0)	//如果输出为负{Out -= 6;		//则直接给输出值减去一个固定偏移}else				//输出为0{Out = 0;		//输出0}

在代码中，固定偏移量是在现实实验中尝试出来的，多次尝试，看出输出值为多少时，转盘才会启动。

3.7.输入死区

在某些系统中，输入的目标值或实际值有微小的噪声波动，或者系统有一定的滞后，这些情况可能会导致执行器在误差很小时频繁调控，不能最终稳定下来，特别是加上输出偏移的式子，输出值很难达到 0。解决方法是设置一个输入死区：若误差绝对值小于一个限度，则固定输出 0，不进行调控，也就是容忍一定的误差存在。当误差小于设定的值，输出值为 0；若大于设定的值，则有输出值。下面是代码实现：

	if (fabs(Error0) < 5)		//如果误差绝对值比较小{Out = 0;				//则直接输出0，不进行调控}else						//否则，即误差绝对值比较大，下面进行正常的PID调控{/*误差积分（累加）*//*如果Ki不为0，才进行误差积分，这样做的目的是便于调试*//*因为在调试时，我们可能先把Ki设置为0，这时积分项无作用，误差消除不了，误差积分会积累到很大的值*//*后续一旦Ki不为0，那么因为误差积分已经积累到很大的值了，这就导致积分项疯狂输出，不利于调试*/if (Ki != 0)				//如果Ki不为0{ErrorInt += Error0;		//进行误差积分}else						//否则{ErrorInt = 0;			//误差积分直接归0}/*PID计算*//*使用位置式PID公式，计算得到输出值*/Out = Kp * Error0 + Ki * ErrorInt + Kd * (Error0 - Error1);/*输出偏移*/if (Out > 0)		//如果输出为正{Out += 6;		//则直接给输出值加上一个固定偏移}else if (Out < 0)	//如果输出为负{Out -= 6;		//则直接给输出值减去一个固定偏移}else				//输出为0{Out = 0;		//输出0}}