当前位置：首页 > news >正文

[Pyro概率编程] 概率分布 | 共轭计算 | 参数存储库

news 2025/8/16 11:40:33

第二章：概率分布

欢迎回来~

在第一章：基础构件中，我们学习了pyro.sample、pyro.param和pyro.plate——构建概率模型的核心指令。

我们了解了pyro.sample如何为程序引入随机性。但当我们调用pyro.sample("flip", dist.Bernoulli(coin_prob))时，其中的dist.Bernoulli部分究竟是什么呢？

这正是概率分布（Distribution）

核心理念

假设我们正在构建描述现实世界的概率模型。现实世界充满不确定性：

抛硬币的结果不总是正面，而是随机的
人的身高不是固定数值，存在个体差异
骰子投掷结果不总是6点，具有随机性

要在模型中表达这些不确定性事件，我们需要描述它们的行为模式：

“这类似一枚正面概率50%的硬币”（伯努利分布）
“这类似平均身高170cm的正态分布”（正态分布）
“这类似六面公平骰子的投掷”（类别分布）

概率分布正是为此而生。它们为pyro.sample提供生成随机值的"蓝图"或"配方"，定义变量的随机模式。

类比定制蛋糕流程：pyro.sample是蛋糕订单，Distribution（如dist.Normal或dist.Bernoulli）是详细配方（例如"三层香草巧克力蛋糕"）。

没有配方，pyro.sample将无法确定生成何种随机数！

Pyro分布的核心概念

Pyro的分布主要基于PyTorch强大的torch.distributions库实现，并扩展了概率编程所需特性。

使用Pyro分布通常包括两个步骤：

定义分布：创建分布实例并指定参数，如dist.Normal(0, 1)定义均值为0、标准差为1的正态分布
与pyro.sample配合使用：将分布对象传递给pyro.sample进行随机采样

🎢常见分布类型

分布类	适用场景	常用参数
`dist.Bernoulli`	二元结果（如抛硬币）	`probs`（结果为1的概率）
`dist.Categorical`	多类别选择（如骰子投掷）	`probs`（各选项的概率分布）
`dist.Normal`	连续型钟形分布数据（如身高）	`loc`（均值），`scale`（标准差）
`dist.Uniform`	均匀分布数值	`low`（最小值），`high`（最大值）
`dist.Poisson`	计数数据（如单位时间事件数）	`rate`（事件平均发生率）

分布对象包含重要方法：

.sample()：从分布中抽取随机值（pyro.sample内部调用）
.log_prob(value)：计算特定值在分布下的对数概率（密度），对推理过程至关重要

分布使用实例

1. 抛硬币（伯努利分布）

Bernoulli分布适用于二元结果，参数probs表示结果为1的概率：

def coin_flip_model_with_dist():# 定义正面概率70%的伯努利分布my_coin_dist = dist.Bernoulli(probs=torch.tensor(0.7))# 从该分布采样（返回0或1）flip_outcome = pyro.sample("my_first_flip", my_coin_dist)return flip_outcome# 多次运行观察不同结果
print(f"结果1: {int(coin_flip_model_with_dist())}")
print(f"结果2: {int(coin_flip_model_with_dist())}")

2. 身高测量（正态分布）

Normal分布适用于连续型数据，参数loc为均值，scale为标准差：

def height_model():# 定义均值170cm、标准差10cm的正态分布my_height_dist = dist.Normal(loc=torch.tensor(170.0), scale=torch.tensor(10.0))# 采样随机身高（浮点数值）random_height = pyro.sample("my_height", my_height_dist)return random_heightprint(f"随机身高采样: {height_model().item():.2f} cm")

3. 骰子投掷（类别分布）

Categorical分布适用于多类别选择，probs为各选项概率张量：

def dice_roll_model():# 六面公平骰子的类别分布my_dice_dist = dist.Categorical(probs=torch.ones(6) / 6.0)# 采样骰子结果（0-5索引转1-6点数）roll_outcome = pyro.sample("my_dice_roll", my_dice_dist)return roll_outcome + 1print(f"骰子点数: {int(dice_roll_model())}")

使用`.log_prob()`方法

此方法计算观测值在分布下的对数概率，对参数学习至关重要：

# 创建正态分布
normal_dist = dist.Normal(loc=torch.tensor(10.0), scale=torch.tensor(2.0))# 计算特定值的对数概率
log_prob_10 = normal_dist.log_prob(torch.tensor(10.0))
print(f"10.0的对数概率: {log_prob_10.item():.2f}")  # 接近均值概率最高log_prob_20 = normal_dist.log_prob(torch.tensor(20.0))
print(f"20.0的对数概率: {log_prob_20.item():.2f}")  # 偏离均值概率骤降

底层实现机制

Pyro分布基于PyTorch实现，并通过TorchDistributionMixin增强功能：

1. PyTorch基础实现

Pyro分布继承自torch.distributions，利用其优化实现：

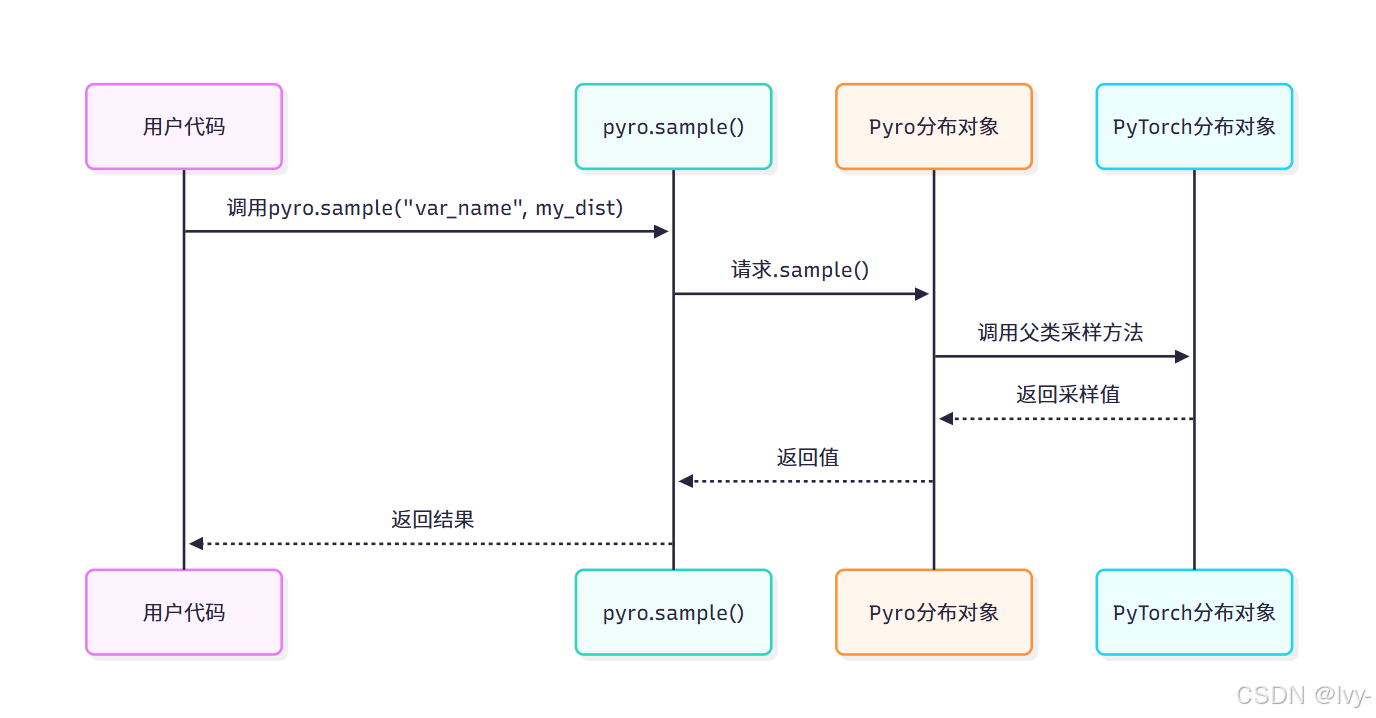
在这里插入图片描述

2. Pyro功能增强

⭕共轭计算

指在复数运算中，将一个复数的虚部符号取反（如 (a + bi) 的共轭为 (a - bi)），用于简化运算或分析对称性。

共轭计算在优化问题中用于快速求解梯度或方向导数，比如机器学习中反向传播算法利用共轭性质高效更新模型参数。

（注：共轭的数学定义涉及复数或矩阵的对称性，实际应用通常聚焦于上述场景。）

应用:

商业场景:

金融风控：银行用共轭梯度法快速解大规模方程组，优化贷款风险评估模型。
物流调度：电商平台通过共轭优化算法规划最短配送路径，降低运输成本。
广告投放：互联网公司利用共轭对偶理论分配广告预算，最大化点击收益。

实际生活:

图像处理：手机拍照的自动美化功能依赖共轭傅里叶变换压缩和修复图像。
医疗影像：MRI扫描使用共轭重建算法快速生成清晰的人体断层图像。
智能推荐：流媒体平台通过共轭矩阵分解预测用户偏好，精准推送内容。

核心价值：将复杂数学问题转化为可高效求解的形式，提升计算速度和资源利用率。

通过TorchDistributionMixin实现：

改进批处理
参数验证
共轭计算优化
与Pyro其他组件协同

代码实现示例：

# pyro/distributions/torch.py 简化片段
class Normal(torch.distributions.Normal, TorchDistributionMixin):pass  # 继承PyTorch实现，添加Pyro特性

总结

概率分布是定义随机变量行为的核心组件。

通过dist模块创建分布对象，并与pyro.sample配合，我们能够精确控制模型中的不确定性。

Pyro在PyTorch基础上进行功能扩展，为概率编程提供强大支持。

在后续章节中，我们将探索如何通过参数存储库学习分布参数，这是构建自适应概率模型的关键步骤。

第三章：参数存储库（ParamStore）

在第二章：概率分布中，我们学习了如何用分布定义概率模型中随机变量的"配方"。

我们了解了pyro.sample如何从分布中抽取样本。

但如果我们需要从数据中学习这些分布的参数呢？例如学习Bernoulli分布的probs参数或Normal分布的loc和scale参数？

在第一章：基础构件中，我们简要介绍了pyro.param作为声明"可学习值"的方式。

但Pyro如何跟踪这些值？如何确保在模型某处声明pyro.param("coin_bias", ...)后，后续调用pyro.param("coin_bias")时能获得完全相同的值？

这正是参数存储库（通常简称ParamStore）的核心作用！

核心理念

设想我们正在构建一个带有多个调节旋钮的复杂机器。每个旋钮控制重要设置，我们需要通过经验学习最佳配置。此时需要中心化存储机制来实现：

集中存储：统一管理所有旋钮（参数）
一致性保证：无论身处机器的哪个模块，调用"旋钮A"始终指向同一实体
生命周期管理：保存配置、加载历史状态或重置参数

Pyro的参数存储库正是为此而生。

它作为全局注册中心，集中管理所有通过pyro.param声明的可学习参数，扮演着参数"银行保险库"的角色。

核心价值在于为每个可学习张量提供唯一命名存储空间，确保参数在模型生命周期内保持全局一致性与可访问性。

让我们回顾第一章的偏置硬币案例：

import pyro
import pyro.distributions as dist
import torchdef learnable_coin_model_param_store_example():# 声明名为"coin_bias"的可学习参数（与存储库交互）coin_bias = pyro.param("coin_bias", torch.tensor(0.5, requires_grad=True))constrained_bias = torch.sigmoid(coin_bias)  # 映射到[0,1]区间flip = pyro.sample("flip", dist.Bernoulli(constrained_bias))return flip# 运行模型以注册参数
_ = learnable_coin_model_param_store_example()# 直接从存储库获取参数
current_bias = pyro.param("coin_bias")
print(f"当前可学习硬币偏置值: {current_bias.item():.2f}")

运行机制：首次调用pyro.param("coin_bias", ...)时，存储库将torch.tensor(0.5)注册为"coin_bias"。后续无论何处调用pyro.param("coin_bias")都将返回同一张量，确保参数一致性。

存储库核心特性

全局访问：存储库是单例对象，模型任意位置可通过参数名访问
命名唯一性：参数名需全局唯一（如"coin_bias"），重复声明同名参数将返回已有值
持久化存储：支持参数快照保存与加载，便于模型训练恢复与部署
自动化管理：通过pyro.param自动处理参数注册与检索，无需手动干预

存储库交互实践

清空存储库

在开发调试时，可能需要重置参数状态：

import pyro
import torch# 清空参数存储库
pyro.clear_param_store()
print("存储库已清空")# 声明新参数（初始值0.1生效）
new_bias = pyro.param("another_bias", torch.tensor(0.1, requires_grad=True))
print(f"新初始化偏置: {new_bias.item():.2f}")# 重复声明将被忽略（仍返回0.1）
ignored_bias = pyro.param("another_bias", torch.tensor(0.9, requires_grad=True))
print(f"尝试重置为0.9，实际值仍为: {ignored_bias.item():.2f}")

参数持久化

实现模型参数的保存与加载：

import pyro
import torch
import os# 清空存储库确保示例纯净
pyro.clear_param_store()# 定义新参数
_ = pyro.param("my_first_param", torch.tensor([1.0, 2.0], requires_grad=True))# 获取存储库实例
param_store = pyro.get_param_store()
filename = "my_trained_params.pt"# 保存参数快照
param_store.save(filename)
print(f"参数已保存至: {filename}")# 模拟新会话加载
pyro.clear_param_store()
param_store.load(filename)
loaded_param = pyro.param("my_first_param")
print(f"加载参数值: {loaded_param.tolist()}")# 清理临时文件
os.remove(filename)

底层实现解析

pyro.param的调用最终由ParamStoreDict类处理，其核心结构包含：

class ParamStoreDict:def __init__(self):self._params = {}      # 存储无约束张量self._constraints = {}# 参数约束条件def setdefault(self, name, init_value, constraint=None):if name not in self._params:# 新参数：转换无约束形式并注册unconstrained = self._convert_to_unconstrained(init_value, constraint)unconstrained.requires_grad_(True)self._params[name] = unconstrainedself._constraints[name] = constraint# 返回约束空间的值（如概率值转换为sigmoid输出）return self._get_constrained_value(name)