300. 最长递增子序列 - 力扣(LeetCode)
Solution
#include<iostream>
#include<vector>
using namespace std;class Solution {
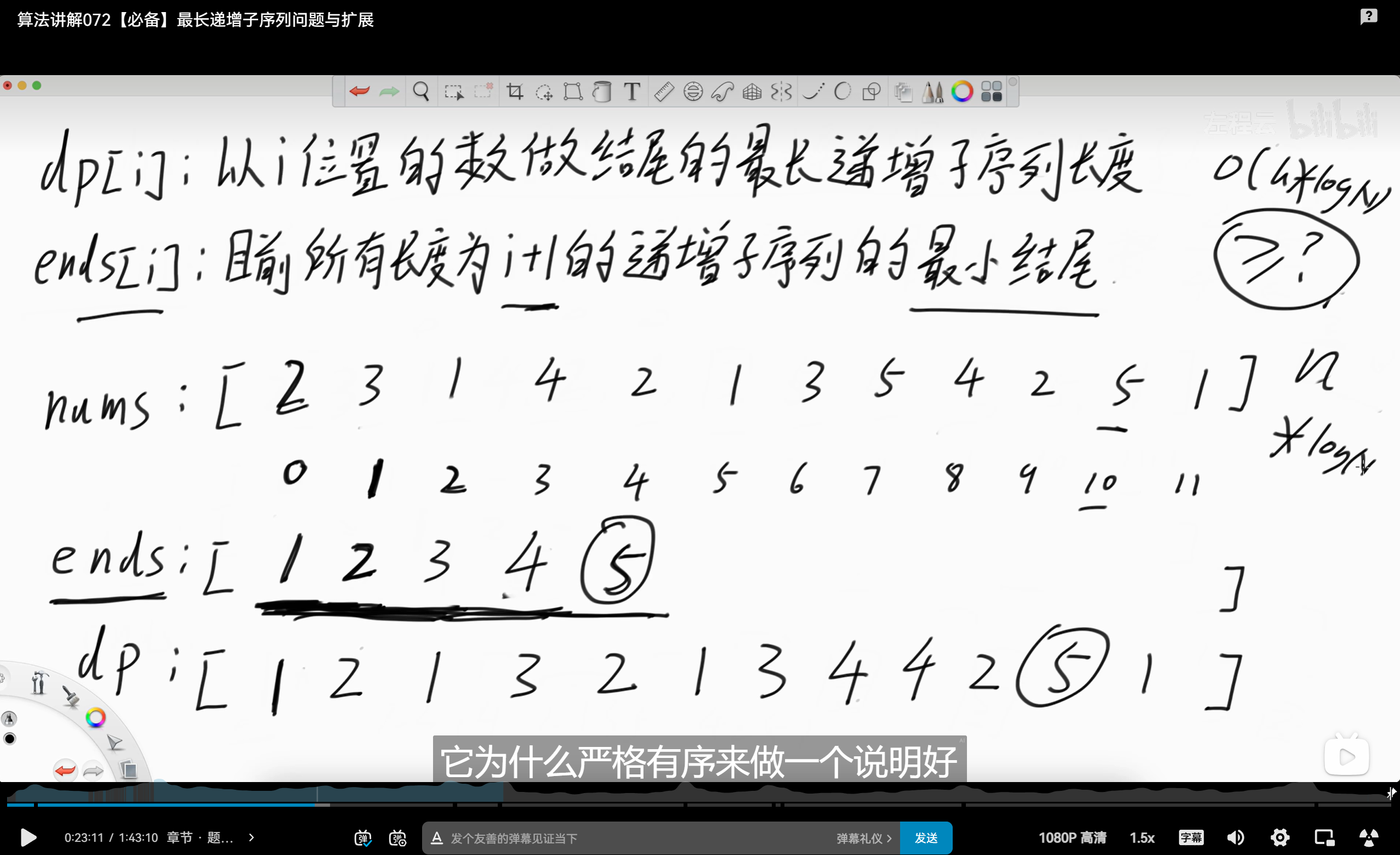
public:const int minf = -1e9;//普通dp做法,时间复杂度O(n^2)int lengthOfLIS1(vector<int>& nums) {int n = nums.size();vector<int>dp(n + 1, 1);int ans = 1;//dp(i)表示以第i个字符结尾的最长递增子序列的长度for (int i = 1; i < n; ++i) {for (int j = 0; j < i; ++j) {if (nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + 1);}ans = max(ans, dp[i]);}return ans;}//优化的dp做法,时间复杂度O(n*logn)//有点难理解,ends数组动态维护了当前长度为各个值的递增子序列的最小末尾值,//当来到一个新的数的时候,如何才能知道以这个数结尾的最长递增子序列的长度是多少,//这样就可以去ends数组里面寻找,寻找一个和该数字最接近的数,说明可以作为该数字的前一个int lengthOfLIS(vector<int>& nums) {int n = nums.size();vector<int>dp(n + 1, 1);vector<int>ends;//ends(i)表示长度为i+1的递增子序列的最小结尾值ends.push_back(nums[0]);for (int i = 1; i < n; ++i) {int cur = nums[i];int index = bs1(ends, cur);if (index == -1) {ends.push_back(cur);}else {ends[index] = cur;}}return ends.size();}//二分查找数组中第一个大于等于v的数的下标,没找到则返回-1int bs1(vector<int>& nums, int v) {int l = 0, r = nums.size() - 1;int ans = -1;while (l <= r) {int mid = (l + r) >> 1;if (nums[mid]>=v) {ans = mid;r = mid - 1;}else {l = mid + 1;}}return ans;}
};
int main() {return 0;
}


