当前位置：首页 > news >正文

机器学习之PCA降维

news 2025/8/16 7:07:17

简介

在机器学习中，高维数据常常像一层迷雾，不仅会增加模型的复杂度、拖慢计算速度，还可能因 “维度灾难” 导致模型性能下降。而 PCA（主成分分析）降维算法，就像一把精准的 “数据手术刀”，能在保留关键信息的同时，剥离冗余维度，让数据变得更简洁、更易处理。我们会从最根本的问题出发：为什么要进行降维？

一、主成分分析（PCA）

什么是主成分分析

就是通用的降维工具，数据的特征又叫做数据的维度，减少数据维度（即降维），是指在尽可能保留数据关键信息的前提下，降低数据特征数量，简化数据集结构

1.1向量的内积:

内积: $(a_1, a_2, \cdots, a_n)^{\mathrm{T}} \cdot (b_1, b_2, \cdots, b_n)^{\mathrm{T}} = a_1b_1 + a_2b_2 + \cdots + a_nb_n$

A 与 B 的内积: $\boldsymbol{A} \cdot \boldsymbol{B} = \vert\boldsymbol{A}\vert\vert\boldsymbol{B}\vert\cos(\alpha)$

$\boldsymbol{A}:(1,3)\) \(\boldsymbol{B}:(3,2)$

$\boldsymbol{A} \cdot \boldsymbol{B} = \sqrt{1 + 3^2} \times \sqrt{3^2 + 2^2} \times \cos(\alpha)$

假设向量 $\boldsymbol{B}$ 的模等于 1，即 $\vert\boldsymbol{B}\vert = 1$ ，此时 $\boldsymbol{A}$ 到\ $\boldsymbol{B}$ 的投影变成了:

$\boldsymbol{A} \cdot \boldsymbol{B} = \vert\boldsymbol{A}\vert\cos(\alpha)$

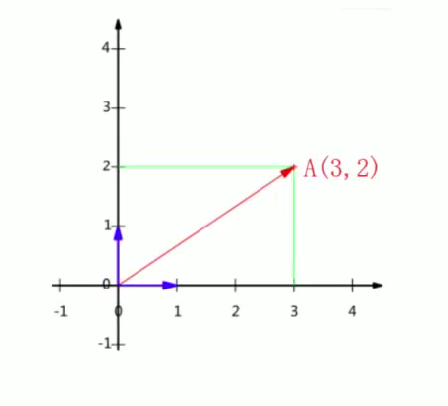
1.2基

定义：基（也称为基底）是描述、刻画向量空间的基本工具。

基： $(1,0)^{\mathrm{T}}$ 与 $(0,1)^{\mathrm{T}}$ 是二维空间的一组基 3. 向量 $(3,2)$ 由这一组基完全表示。
$\begin{pmatrix} \boldsymbol{1} & \boldsymbol{0}\\ \boldsymbol{0} & \boldsymbol{1} \end{pmatrix} *\begin{pmatrix} \boldsymbol{3}\\ \boldsymbol{2} \end{pmatrix} = \begin{pmatrix} \boldsymbol{3}\\ \boldsymbol{2} \end{pmatrix}$
基的条件： 4. 什么样的向量可以成为基？
任何两个线性无关的二维向量都可以成为一组基

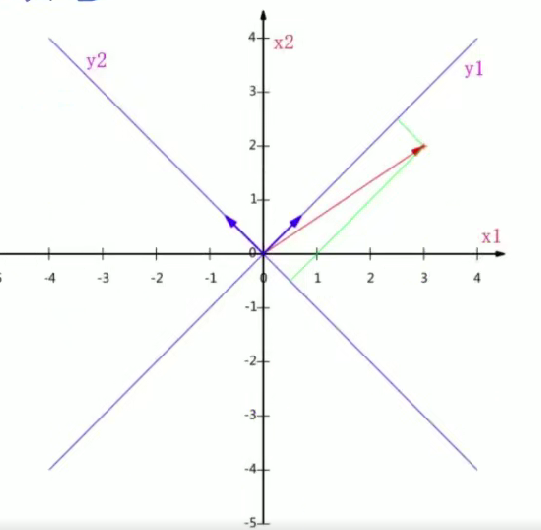
1.3基变换:

新的一组基:

$\boldsymbol{y_1} = \begin{pmatrix} \boldsymbol{1} \\ \boldsymbol{1} \end{pmatrix}, \quad \boldsymbol{y_2} = \begin{pmatrix} \boldsymbol{-1} \\ \boldsymbol{1} \end{pmatrix}$

变换成模为 $\boldsymbol{1}$ 的新基：

$\boldsymbol{y_1} = \begin{pmatrix} \boldsymbol{\dfrac{1}{\sqrt{2}}} \\ \boldsymbol{\dfrac{1}{\sqrt{2}}} \end{pmatrix}, \quad \boldsymbol{y_2} = \begin{pmatrix} \boldsymbol{\dfrac{-1}{\sqrt{2}}} \\ \boldsymbol{\dfrac{1}{\sqrt{2}}} \end{pmatrix}$

将(3,2)映射到新的基上:
由于新的基的模是1，所以直接相乘可得结果 (内积的定义):

$\begin{pmatrix} \boldsymbol{y_1} \\ \boldsymbol{y_2} \end{pmatrix} = \begin{pmatrix} \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ -\dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} = \begin{pmatrix} \dfrac{5}{\sqrt{2}} \\ -\dfrac{1}{\sqrt{2}} \end{pmatrix}$

对于多个二维向量:

$\begin{pmatrix} \boldsymbol{y_1} \\ \boldsymbol{y_2} \end{pmatrix} \begin{pmatrix} \dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \\ -\dfrac{\sqrt{2}}{2} & \dfrac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} \boldsymbol{1} & \boldsymbol{2} & \boldsymbol{3} \\ \boldsymbol{1} & \boldsymbol{2} & \boldsymbol{3} \end{pmatrix} = \begin{pmatrix} \boldsymbol{\sqrt{2}} & \boldsymbol{2\sqrt{2}} & \boldsymbol{3\sqrt{2}} \\ \boldsymbol{0} & \boldsymbol{0} & \boldsymbol{0} \end{pmatrix}$

推广到 m 个 N 维向量的变换：

$\begin{pmatrix} \boldsymbol{p_1} \\ \boldsymbol{p_2} \\ \vdots \\ \boldsymbol{p_R} \end{pmatrix} \begin{pmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & \cdots & \boldsymbol{a_M} \end{pmatrix} = \begin{pmatrix} \boldsymbol{p_1a_1} & \boldsymbol{p_1a_2} & \cdots & \boldsymbol{p_1a_M} \\ \boldsymbol{p_2a_1} & \boldsymbol{p_2a_2} & \cdots & \boldsymbol{p_2a_M} \\ \vdots & \vdots & \ddots & \vdots \\ \boldsymbol{p_Ra_1} & \boldsymbol{p_Ra_2} & \cdots & \boldsymbol{p_Ra_M} \end{pmatrix}$

其中 $\boldsymbol{p_i}$ 为行， $\boldsymbol{a_j}$ 为列

1.4基变换的含义:

两个矩阵相乘的意义是将每一列右边矩阵中的列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。
抽象地说，一个矩阵可以表示一种线性变换。

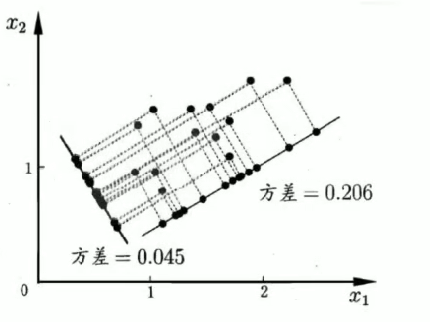
如何选择基才是最优的？或者说，如何才能有效地保留较多的原始数据信息。

方差最大的方向即为最优基。

我们希望投影后投影值尽可能分散，而这种分散程度，可以用数学上的方差来表述。

1.5方差公式：

$\text{Var}(a) = \frac{1}{m} \sum_{i = 1}^{m} (a_i - \mu)^2$

数据特征（维度）减去均值

$\begin{matrix} \text{dim1} & \begin{pmatrix} 1 & 1 & 2 & 4 & 2 \end{pmatrix} \\ \text{dim2} & \begin{pmatrix} 1 & 3 & 3 & 4 & 4 \end{pmatrix} \end{matrix}$

dim1 均值 $\boldsymbol{2}$ ，处理后： $\begin{pmatrix} -1 & -1 & 0 & 2 & 0 \end{pmatrix}$

dim2 均值 $\boldsymbol{3}$ ，处理后： $\begin{pmatrix} -2 & 0 & 0 & 1 & 1 \end{pmatrix}$

问题转化

寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。（对于二维变一维来说）

对于三维数据来说，将数据降到二维，寻找的基为方差最大的方向，再次将数据降到一维呢？这个基是什么？必然与降到二维的基无限接近。

方差次大。
这样的一个基是没有用的，我们应该让两个基线性无关【线性无关才能保留更多的原始信息】

1.6协方差

公式：

原始： $\boldsymbol{Cov(a_j, b_i) = \dfrac{1}{m}\sum_{i = 0}^{m}(a_j - \mu_1)(b_i - \mu_2)}$

均值为 $\boldsymbol{0}$ 时简化： $\boldsymbol{Cov(a_j, b_i) = \dfrac{1}{m}\sum_{i = 0}^{m}(a_j)(b_i)}$

含义：表征两个字段之间的相关性。
当协方差为 $\boldsymbol{0}$ 时，表示两个字段完全独立。

利用协方差为 $\boldsymbol{0}$ ，选择另一组基，这组基的方向一定与第一组基正交。

1.7协方差矩阵

定义：
假设我们有 $\boldsymbol{a}$ ， $\boldsymbol{b}$ 两个字段，组成矩阵：

$\boldsymbol{X}\)\(X = \begin{pmatrix} a_1 & a_2 & \cdots & a_m \\ b_1 & b_2 & \cdots & b_m \end{pmatrix}$

用 $\boldsymbol{X}$ 乘以其转置，并乘以 $\boldsymbol{1/m}$ ：

$\frac{1}{m} X X^{\mathrm{T}} = \begin{pmatrix} \frac{1}{m} \sum_{i=1}^{m} a_i^2 & \frac{1}{m} \sum_{i=1}^{m} a_i b_i \\ \frac{1}{m} \sum_{i=1}^{m} a_i b_i & \frac{1}{m} \sum_{i=1}^{m} b_i^2 \end{pmatrix}$

对于更高维度的数据，上述结论依然成立。

目标

除主对角线上的元素外，都为 $\boldsymbol{0}$ ，并且方差从大到小排列。

1.8协方差矩阵对角化

变量说明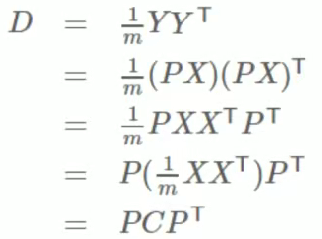
- 原始数据： $\boldsymbol{X}$ → 协方差矩阵： $\boldsymbol{C}$
- 一组基按行组成的矩阵： $\boldsymbol{P}$
- 基变换后的数据： $\boldsymbol{Y}$ → 协方差矩阵： $\boldsymbol{D}$
- 隐含信息： $\boldsymbol{Y = PX}$

寻找一个矩阵 $\boldsymbol{P}$ ，满足\ $\boldsymbol{PCP^{\mathrm{T}}}$ 是一个对角矩阵，并且对角元素按从大到小依次排列。
此时， $\boldsymbol{P}$ 的前 $\boldsymbol{K}$ 行就是要寻找的基；用\ $\boldsymbol{P}$ 的前\ $\boldsymbol{K}$ 行组成的矩阵乘以 $\boldsymbol{X}$ ，可使\ $\boldsymbol{X}$ 从 $\boldsymbol{N}$ 维降到 $\boldsymbol{K}$ 维，满足 “协方差矩阵对角化 + 方差降序” 的优化条件。、

1.9协方差矩阵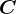 $\boldsymbol{C}$ 对角化

公式： $\boldsymbol{D = PCP^{\mathrm{T}}}$ ，其中 $\boldsymbol{C = \dfrac{1}{m} XX^{\mathrm{T}}}$

实对称矩阵特性：若 $\boldsymbol{C}$ 是实对称矩阵，则存在正交矩阵 $\boldsymbol{E}$ ，使得：
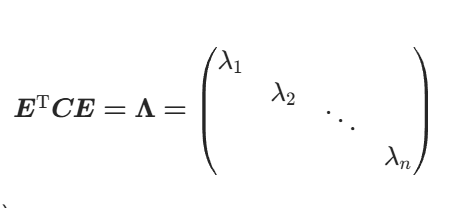
为对角矩阵，对角线元素 $\boldsymbol{\lambda_i}$ 是 $\boldsymbol{C}$ 的特征值

终极目标找到

核心公式：

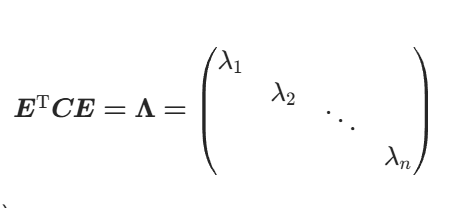
终极目标： $\boldsymbol{P = E^{\mathrm{T}}}$

$\boldsymbol{P}$ 的定义： $\boldsymbol{P}$ 是协方差矩阵 $\boldsymbol{C}$ 的特征向量单位化后按行排列出的矩阵，其中每一行都是 $\boldsymbol{C}$ 的一个特征向量。

二、计算案例

1. 执行第一步与第二步

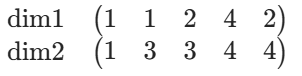
数据 $\boldsymbol{a}\boldsymbol{b}\boldsymbol{c}\boldsymbol{d}\boldsymbol{e}$ ：

dim1 均值 $\boldsymbol{2}$ ，处理后： $\boldsymbol{\begin{pmatrix} -1 & -1 & 0 & 2 & 0 \end{pmatrix}}$
dim2 均值 $\boldsymbol{3}$ ，处理后： $\boldsymbol{\begin{pmatrix} -2 & 0 & 0 & 1 & 1 \end{pmatrix}}$

2. 计算协方差矩阵

协方差矩阵C的计算：

$C = \frac{1}{5} \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} \begin{pmatrix} -1 & -2 \\ -1 & 0 \\ 0 & 0 \\ 2 & 1 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} \frac{6}{5} & \frac{4}{5} \\ \frac{4}{5} & \frac{6}{5} \end{pmatrix}$

3. 计算协方差矩阵的特征值与特征向量

特征方程 $\boldsymbol{A}$ 为协方差矩阵，这里 $\boldsymbol{A = \begin{pmatrix} \dfrac{6}{5} & \dfrac{4}{5} \\ \dfrac{4}{5} & \dfrac{6}{5} \end{pmatrix}}$

$|\lambda E - A| = \begin{vmatrix} \lambda - \dfrac{6}{5} & -\dfrac{4}{5} \\ -\dfrac{4}{5} & \lambda - \dfrac{6}{5} \end{vmatrix} = \begin{vmatrix} 5\lambda - 6 & -4 \\ -4 & 5\lambda - 6 \end{vmatrix}$

求解特征值：

展开行列式得： $(5\lambda - 6)^2 - 4^2 = 0$

解得特征值： $\boldsymbol{\lambda_1 = 2}$ $\boldsymbol{\lambda_2 = \dfrac{2}{5}}$

求特征向量：

当 $\boldsymbol{\lambda_1 = 2}$ 时：经初等变换得： $\begin{vmatrix} 4 & -4 \\ -4 & 4 \end{vmatrix} \to \begin{vmatrix} 1 & -1 \\ 0 & 0 \end{vmatrix}$

对应方程： $\boldsymbol{x_1 - x_2 = 0}$

特征向量： $\boldsymbol{c_1 = \begin{pmatrix} 1 \\ 1 \end{pmatrix}}$ 单位化后： $\boldsymbol{\begin{pmatrix} \dfrac{\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} \end{pmatrix}}$

当 $\boldsymbol{\lambda_2 = \dfrac{2}{5}}$ 时，特征向量：
$\boldsymbol{c_2 = \begin{pmatrix} -1 \\ 1 \end{pmatrix}}$ 单位化后 $\boldsymbol{\begin{pmatrix} \dfrac{-\sqrt{2}}{2} \\ \dfrac{\sqrt{2}}{2} \end{pmatrix}}$

4.矩阵 $\boldsymbol{P}$

$P = \begin{pmatrix} \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \\ -\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{pmatrix}$

对角化验证：

计算 $\boldsymbol{PCP^{\mathrm{T}}}$ 为协方差矩阵， $\boldsymbol{C = \begin{pmatrix} \dfrac{6}{5} & \dfrac{4}{5} \\ \dfrac{4}{5} & \dfrac{6}{5} \end{pmatrix}}$ ：

$PCP^{\mathrm{T}} = \begin{pmatrix} \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \\ -\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} \dfrac{6}{5} & \dfrac{4}{5} \\ \dfrac{4}{5} & \dfrac{6}{5} \end{pmatrix} \begin{pmatrix} \dfrac{1}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} \\ \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & \dfrac{2}{5} \end{pmatrix}$

5.基变换后的数据 $\boldsymbol{Y}$ ：

用\ $\boldsymbol{P}$ 的行向量对去均值后的数据 $\boldsymbol{\begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix}}$ 做变换：

$Y = \begin{pmatrix} \dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \\ -\dfrac{1}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} -1 & -1 & 0 & 2 & 0 \\ -2 & 0 & 0 & 1 & 1 \end{pmatrix} = \begin{pmatrix} -\dfrac{3}{\sqrt{2}} & -\dfrac{1}{\sqrt{2}} & 0 & \dfrac{3}{\sqrt{2}} & \dfrac{1}{\sqrt{2}} \end{pmatrix}$

三、PCA的优缺点

优点

计算方法简单，容易实现。
可以减少指标筛选的工作量。
消除变量间的多重共线性。
在一定程度上能减少噪声数据。

缺点

特征必须是连续型变量。
无法解释降维后的数据是什么。
贡献率小的成分有可能更重要。

四、PCA的API

class PCA:def __init__(self, n_components=None, copy=True, whiten=False, svd_solver='auto', tol=0.0, iterated_power='auto', random_state=None):self.n_components = n_componentsself.copy = copyself.whiten = whitenself.svd_solver = svd_solverself.tol = tolself.iterated_power = iterated_powerself.random_state = random_state

参数解释

n_components：
- 作用：用于指定 PCA 降维后的特征维度数目。
- 取值说明：
  - 若为整数，比如 n_components=5，就是把原始数据直接降维到 5 维，适用于明确知道目标维度的场景，像 10 维数据想降到 5 维分析时设置该整数。
  - 若为小数（范围一般 0 到 1 ），例如 n_components=0.9，表示要让降维后的数据累计方差百分比达到 90% ，算法会自动选择合适的维度数来满足这个方差要求，方便在不想手动指定维度，又希望保留一定比例数据信息时使用。
copy：
- 类型：布尔值（bool ），可选 True 或 False ，默认 True。
- 意义：决定运行 PCA 算法时是否复制原始训练数据。
- 不同取值行为：
  - copy=True：会复制一份原始训练数据，在副本上进行 PCA 运算，这样原始数据的值在算法运行后不会改变，能保证原始数据的完整性，后续若还需用原始数据做其他操作不受影响。
  - copy=False：直接在原始训练数据上进行降维计算，运行后原始数据的值会被改变，优点是能节省内存（不用额外存副本），但要注意后续不能再直接使用原始数据原本的值了。
whiten：
- 作用：判断是否对数据进行白化操作。
- 白化含义：对白化后的每个特征做归一化，让特征方差都变为 1 ，可以去除特征间的相关性且统一特征尺度。
- 取值与场景：默认 False 即不进行白化。一般单纯 PCA 降维本身不需要白化；但如果 PCA 降维后还有后续数据处理（比如作为输入给对特征尺度敏感的模型），可考虑设 True 进行白化，不过会增加计算和存储开销（因为要对数据做额外变换）。
svd_solver：
- 作用：指定奇异值分解（SVD ）的方法，因为 PCA 底层常用 SVD 实现（特征分解是 SVD 特例）。
- 可选值：有 'auto'、'full'、'arpack'、'randomized' 这几个选项。
- 各值特点：
  - 'auto'：算法自动根据数据情况选择合适的 SVD 求解器，是常用且方便的选择，一般数据集都适用。
  - 'full'：传统意义上的 SVD ，使用 scipy 等库的完整 SVD 实现，在数据量不大、维度不特别高时稳定可靠，但数据量大时可能计算慢。
  - 'arpack'：借助 ARPACK 库实现的 SVD ，适用于计算部分奇异值（比如数据是稀疏矩阵等情况），在特定场景下更高效。
  - 'randomized'：使用随机算法加速 SVD ，适合数据量大、数据维度多同时主成分数目比例较低的 PCA 降维，能大幅减少计算时间和资源消耗，不过理论精度可能稍低，但实际很多场景下足够用。
tol：
- 作用：主要在一些迭代求解 SVD 等过程中使用（比如 svd_solver='arpack' 时），用于设置收敛 tolerance（容差），控制迭代精度，默认 0.0 ，一般不用特意修改，算法会按默认策略处理收敛判断。
iterated_power：
- 作用：当 svd_solver='randomized' 时，用于设置随机 SVD 中迭代的次数，默认 'auto' ，算法会自动根据情况选择合适的迭代次数来平衡计算效率和精度。
random_state：
- 作用：用于设置随机数生成器的种子，保证结果可复现。
- 场景：当使用像 svd_solver='randomized' 等涉及随机过程的求解器时，设置固定 random_state（比如 random_state=42 ），每次运行 PCA 得到的结果就会一致，方便调试、对比实验等。

Attributes 属性

components_：类型为 array，形状是 (n_components, n_features) ，表示主成分系数矩阵。
explained_variance_：降维后的各主成分的方差值。方差值越大，说明对应的主成分越重要。
explained_variance_ratio_：降维后的各主成分的方差值占总方差值的比例。这个比例越大，主成分越重要。【一般看比例即可（比如通常关注累计比例是否 $> 90\%$ ）】

五、案例分析

这个案例使用的是银行贷款的案例，使用的算法是基于逻辑回归来完成的，除了PCA降维模块，其他代码分析详细见下面文章

机器学习第三课之逻辑回归（一）LogisticRegression

机器学习第三课之逻辑回归（二）LogisticRegression

机器学习第三课之逻辑回归（三）LogisticRegression

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from  sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metricsfrom sklearn.model_selection import cross_val_scoredata=pd.read_csv("creditcard.csv")scaler=StandardScaler()
data["Amount"]=scaler.fit_transform(data[["Amount"]])
data=data.drop(["Time"],axis=1)x=data.iloc[:, :-1]
y=data.iloc[:, -1]pca = PCA(n_components=25)
pca.fit(x)# 打印特征占比相关信息
print('特征所占百分比:{}'.format(sum(pca.explained_variance_ratio_)))
print(pca.explained_variance_ratio_)# 执行降维并打印结果
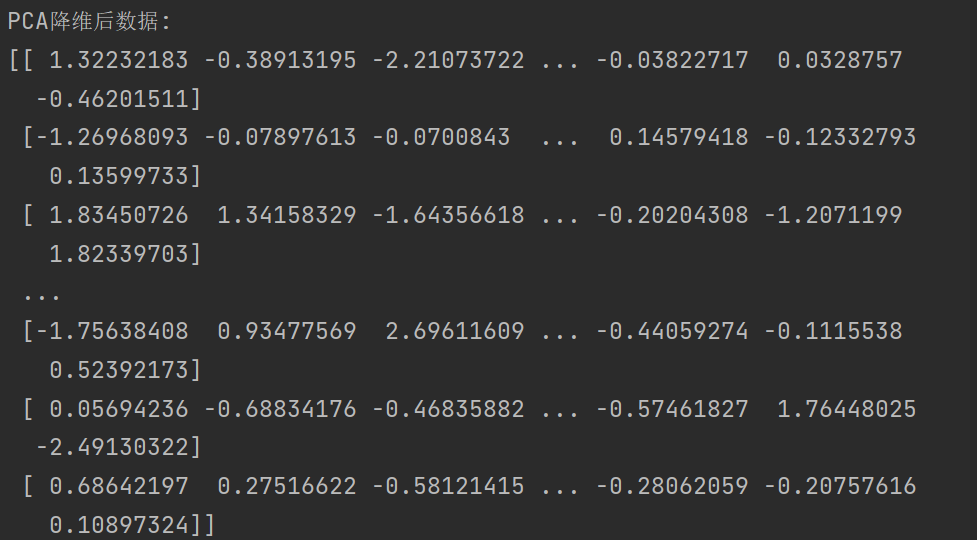
print('PCA降维后数据:')
new_x = pca.transform(x)
print(new_x)x_train_w,x_test_w,y_train_w,y_test_w=train_test_split(new_x,y,test_size=0.2,random_state=0)from imblearn.over_sampling import SMOTE
oversampler=SMOTE(random_state=0)
os_x_train,os_y_train=oversampler.fit_resample(x_train_w,y_train_w)
os_x_train_w,os_x_test_w,os_y_train_w,os_y_test_w=train_test_split(os_x_train,os_y_train,test_size=0.2,random_state=0)scores = []
c_param_range = [0.01, 0.1, 1, 10, 100]
for i in c_param_range:lr = LogisticRegression(C=i, penalty="l2", solver='lbfgs', max_iter=10000)# 使用平衡后的数据集进行交叉验证score = cross_val_score(lr,os_x_train_w, os_y_train_w, cv=8, scoring="recall")score_mean = sum(score) / len(score)scores.append(score_mean)print(f"C等于{i}的召回率为{score_mean}")best_c=c_param_range[np.argmax(scores)]
print("最好的c是：",best_c)estimator=LogisticRegression(C=best_c)
estimator.fit(os_x_train_w,os_y_train_w)
test_predicted=estimator.predict(x_test_w)print(metrics.classification_report(y_test_w,test_predicted))

PCA 实例化：

pca = PCA(n_components=20)

创建了一个 PCA（主成分分析）对象，指定n_components=20表示希望将原始特征降维到 20个主成分。

拟合数据：

pca.fit(x)

使用原始特征数据x来训练 PCA 模型。这一步会计算数据的协方差矩阵，然后进行特征分解（或 SVD 分解），得到可以解释数据最大方差的主成分方向。

查看解释方差比例：

print('特征所占百分比:{}'.format(sum(pca.explained_variance_ratio_)))
print(pca.explained_variance_ratio_)

explained_variance_ratio_属性存储了每个主成分所解释的方差占总方差的比例
第一行打印的是前 25 个主成分解释的方差比例之和，反映了降维后保留的信息量
第二行打印每个主成分单独的解释方差比例

执行降维转换：

new_x = pca.transform(x)


使用训练好的 PCA 模型对原始特征数据x进行转换，将其映射到新的 20 维主成分空间，得到降维后的特征矩阵new_x

打印降维结果：

print('PCA降维后数据:')
print(new_x)

输出降维后的数据集，此时数据已从原始维度（根据 creditcard.csv 实际情况，应为 29 维）降至 20维，同时尽可能保留了原始数据的信息。

查看全文

http://www.dtcms.com/a/332736.html

uniapp 开发微信小程序，获取经纬度并且转化详细地址（单独封装版本）

week1-[顺序结构]跑道

IStoreOS(OpenWrt)开启IPV6

设备数据采集服务器软件TOP Server OPC Server详细介绍

wsl安装完美教程

Vulnhub Deathnote靶机复现攻略

告别手动优化！React Compiler 自动记忆化技术深度解析

16进制pcm数据转py波形脚本

Vim 常用快捷键及插件

关于simplifyweibo_4_moods数据集的分类问题

大白话解析“入口点合约”

Linux系统--库制作与原理

Java—注解

mysql-条件查询案例

zabbix部署问题后常见问题

Codeforces 无路可走

分布式系统设计的容错机制

AI优质信息源汇总：含X账号，Newsletter，播客，App

如何在 FastAPI 中玩转 APScheduler，让任务定时自动执行？

上下文块嵌入(contextualized-chunk-embeddings)

collections：容器数据类型

C语言——深入理解指针（四）

完整技术栈分享：基于Hadoop+Spark的在线教育投融资大数据可视化分析系统

使用XXL-SSO实现登录认证以及权限管控

解决 MySQL 查询速度缓慢的问题

Filebeat 轻量级日志采集实践：安装、配置、多行合并、JSON 解析与字段处理

Java集合Map与Stream流：Map实现类特点、遍历方式、Stream流操作及Collections工具类方法

【软件设计模式】前置知识类图、七大原则（精简笔记版）

C++ 调试报错常量中有换行符

基于桥梁三维模型的无人机检测路径规划系统设计与实现

简介