LeetCode Day6 -- 图
目录
1. 图
1.1 python实现:邻接表、邻接矩阵
1.2 应用场景
2. BFS & DFS
2.1 广度优先搜索BFS
2.2 深度优先搜索DFS
3.Leetcode
3.1 图的连通性问题
(1)841 钥匙和房间
(2)547 省份数量
(3)1466 重新规划路线
(4)200 岛屿数量
3.2 BFS解决二维矩阵中的问题
(1)1926 迷宫中离入口最近的出口
(2)994 腐烂的橘子
3.3 带权图
(1)399 除法求值
3.4 拓扑排序
(1)207 课程表
1. 图
1.1 python实现:邻接表、邻接矩阵
(1)邻接表(常用:节省空间,适合稀疏图)
graph = {'A': ['B', 'C'], # 无向图邻居'B': ['A', 'C', 'D'],'C': ['A', 'B'],'D': ['B']
}""" 带权图的邻接表 """
weighted_graph = {'A': {'B': 2, 'C': 4},'B': {'C': 1, 'D': 7}
}(2)邻接矩阵(适合稠密图)
matrix = [[0, 1, 1, 0], # A的邻居:B、C[1, 0, 1, 1], # B的邻居:A、C、D[1, 1, 0, 0], # C的邻居:A、B[0, 1, 0, 0] # D的邻居:B
]1.2 应用场景
| 场景 | 问题类型 | 实现思路 |
|---|---|---|
| 路径规划 | 最短路径 | Dijkstra(非负权)、Bellman-Ford(负权) |
| 社交网络 | 好友推荐 | BFS查找K度好友,社区检测(DFS连通分量) |
| 任务调度 | 依赖排序 | 拓扑排序(有向无环图) |
| 网络分析 | 广播消息 | BFS模拟消息扩散 |
| AI寻路 | 状态转移 | DFS回溯(如迷宫) |
2. BFS & DFS
2.1 广度优先搜索BFS
(1)过程:逐层遍历,用队列实现。
(2)应用场景:最短路径(无权图)、层级遍历、拓扑排序(Kahn算法)、扩散传播等
from collections import dequedef bfs(graph, start):visited = set([start])queue = deque([start])while queue:vertex = queue.popleft()for neighbor in graph[vertex]:if neighbor not in visited:visited.add(neighbor)queue.append(neighbor)return visited # 返回所有可达节点2.2 深度优先搜索DFS
(1)过程:递归深入路径,用栈实现。
(2)应用场景:路径存在性检测(如迷宫)、拓扑排序(有向无环图)、连通分量统计、环检测(递归栈)、回溯问题等
""" 递归版 """
def dfs_recursive(graph, start, visited=None):if visited is None:visited = set()visited.add(start)for neighbor in graph[start]:if neighbor not in visited:dfs_recursive(graph, neighbor, visited)return visited""" 迭代版(栈实现)"""
def dfs_iterative(graph, start):visited = set()stack = [start]while stack:vertex = stack.pop()if vertex not in visited:visited.add(vertex)stack.extend(reversed(graph[vertex])) # 保持原顺序return visited3.Leetcode
3.1 图的连通性问题
(1)841 钥匙和房间
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。当你进入一个房间,你可能会在里面找到一套 不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
BFS方案:
from collections import deque
class Solution(object):def canVisitAllRooms(self, rooms):""":type rooms: List[List[int]]:rtype: bool"""n=len(rooms)visited=[False]*n## 从0号房开始BFSquene = deque([0])visited[0]=Truewhile quene:cur_room = quene.popleft() ##当前房间号for key in rooms[cur_room]: ## 遍历当前房间内的钥匙if not visited[key]:visited[key]=Truequene.append(key)return all(visited)DFS方案:
n=len(rooms)visited=[False]*ndef dfs(room):visited[room]=True ## 能开当前room,visited=truefor key in rooms[room]: ## 看当前room中有哪些keyif not visited[key]: ## 如果key对应的房间没被开过,去开当前key对应的房间dfs(key)dfs(0) ## 从0号房开始DFSreturn all(visited)(2)547 省份数量
省份的定义是一组直接或间接相连的城市(即一个连通分量)→ 求无向图中连通分量的个数
BFS方案:
n=len(isConnected)
visited=[False]*n
count=0for i in range(n):if not visited[i]: ## 找到未标记省份count+=1quene=deque([i]) ## 找省份内的其他城市(找整个连通分量)while quene:city=quene.popleft()for neighbor in range(n):if isConnected[city][neighbor]==1 and not visited[neighbor]:visited[neighbor]=Truequene.append(neighbor)
return countDFS方案:
class Solution(object):def findCircleNum(self, isConnected):""":type isConnected: List[List[int]]:rtype: int"""n = len(isConnected)visited = [False]*ncount = 0def dfs(city):visited[city]=True## 遍历该城市的所有邻居for neighbor in range(n):## 如果是邻居且未被访问过,继续递归,直到找到这一条完整的连通分量if isConnected[city][neighbor]==1 and not visited[neighbor]:visited[neighbor]=Truedfs(neighbor)for i in range(n):if not visited[i]:count+=1 ## 找到未标记的省份dfs(i) ## 找到该省份内的所有城市return count(3)1466 重新规划路线
重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
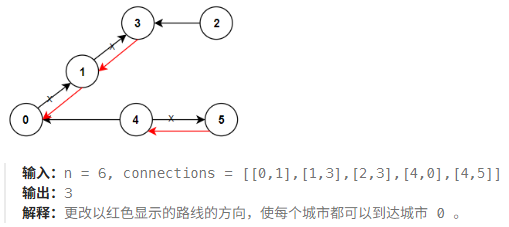
1. 构建图结构:创建一个无向图,包含所有节点及其连接关系
2. 方向判断:在遍历过程中,对每条边:
-- 如果原始方向是从父节点指向当前节点,说明方向正确
-- 如果原始方向是从当前节点指向父节点,说明方向需要反转
BFS方案:
from collections import deque
class Solution(object):def minReorder(self, n, connections):""":type n: int:type connections: List[List[int]]:rtype: int"""graph = [[] for _ in range(n)]edges = set() ## 存放边的方向for i, j in connections:graph[i].append(j)graph[j].append(i)edges.add((i,j)) ## 需要翻转的原始有向边(i→j)count=0visited=[False]*nvisited[0]=Truequene=deque([0])while quene:i=quene.popleft()for j in graph[i]: ## j是当前节点的邻居if not visited[j]: visited[j]=Truequene.append(j)if (i,j) in edges:count+=1return countDFS方案:
class Solution(object):def minReorder(self, n, connections):""":type n: int:type connections: List[List[int]]:rtype: int"""graph = [[] for _ in range(n)]for i, j in connections:graph[i].append((j, True)) ## i→j:背离0节点的方向,需要翻转graph[j].append((i, False)) ## j→i:无需翻转print(graph)visited=[False]*nvisited[0]=Trueself.count=0def dfs(node):for neighbor, need_flip in graph[node]:if not visited[neighbor]:visited[neighbor]=Trueif need_flip:self.count+=1dfs(neighbor)dfs(0)return self.count(4)200 岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
from collections import deque
class Solution(object):def numIslands(self, grid):""":type grid: List[List[str]]:rtype: int"""m, n= len(grid), len(grid[0]) ## m-行,n-列directions=[(0,1), (0,-1), (1,0), (-1,0)]visited = [[False]*n for _ in range(m)]island=0for i in range(m):for j in range(n):if grid[i][j]=='1': ## 发现未访问的陆地island+=1 grid[i][j]='0' ## 标记为水 → 相当于已访问## 找和当前陆地连接的其他陆地(找连通分量,看能形成多大的岛)quene=deque()quene.append((i,j))while quene:row, col = quene.popleft()for dr,dc in directions: ## 往四个方向延伸cur_row, cur_col = dr+row, dc+col## 检查新位置是否是有效的陆地if 0<=cur_row<m and 0<=cur_col<n and grid[cur_row][cur_col]=='1':grid[cur_row][cur_col]='0'quene.append((cur_row,cur_col))return island3.2 BFS解决二维矩阵中的问题
(1)1926 迷宫中离入口最近的出口

1. 初始化:从入口点开始 BFS
2. 遍历方向:每次可移动上、下、左、右四个方向
3. 边界条件:不能进入墙(“+”)、不能超出迷宫边界、已访问过的点不再访问
4. 终止条件:到达迷宫边界上的空格子(且不是入口点)
from collections import deque
class Solution(object):def nearestExit(self, maze, entrance):""":type maze: List[List[str]]:type entrance: List[int]:rtype: int"""m=len(maze) ## 行n=len(maze[0]) ## 列directions=[(-1,0),(1,0),(0,-1),(0,1)] ## 下一步要尝试的方向(上下左右)visited=[[False]*n for _ in range(m)] ## 创建m*n的visited存储访问标记steps=0quene=deque()start_row, start_col = entrance[0], entrance[1] ## 初始位置visited[start_row][start_col]=Truequene.append((start_row, start_col, steps))while quene:row, col, steps = quene.popleft()""" 判断是否到达出口(非起点的边界处)"""is_boundary = (row==0 or row==m-1 or col==0 or col==n-1)is_start = (row==start_row and col==start_col)""" 若找到出口 """if is_boundary and not is_start:return steps""" 没找到出口,继续向上下左右四个方向分别查找 """for dr,dc in directions:cur_row, cur_col = dr+row, dc+col ## 下一步的位置""" 下一步的位置是否在范围内 """if 0<=cur_row<m and 0<=cur_col<n:""" 若是范围内还没走过的地方,看能不能走 """if not visited[cur_row][cur_col] and maze[cur_row][cur_col]=='.':visited[cur_row][cur_col]=Truequene.append(((cur_row, cur_col, steps+1)))return -1(2)994 腐烂的橘子
每分钟,腐烂的橘子周围 4 个方向上相邻的新鲜橘子都会腐烂。返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
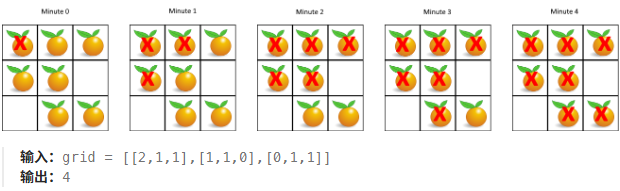
1. 时间统计:该按层处理,同一层的橘子同时腐烂(同1分钟)
2. 访问标记:不需要独立visited数组,可直接用grid值判断(grid=2 → visited=True)
from collections import deque
class Solution(object):def orangesRotting(self, grid):""":type grid: List[List[int]]:rtype: int"""m, n = len(grid), len(grid[0]) ## 行,列visited=[[False]*n for _ in range(m)]directions=[(0,1), (0,-1), (1,0), (-1,0)]minutes=-1 ## 初始为-1,第一次循环变为0fresh_nums=0 ## 新鲜橘子数quene=deque()for i in range(m):for j in range(n):if(grid[i][j]==2): ## 腐烂橘子入队(可能不止一个)quene.append((i,j)) elif(grid[i][j]==1): ## 统计新鲜橘子数目fresh_nums += 1""" 本身就没有新鲜的橘子,直接返回0 """if fresh_nums==0: return 0while quene:""" 当前有size个腐烂橘子,同时发力腐烂新鲜的 """size = len(quene) for _ in range(size):row, col= quene.popleft() for dr,dc in directions:cur_row, cur_col = dr+row, dc+colif 0<=cur_row<m and 0<=cur_col<n:if grid[cur_row][cur_col]==1:grid[cur_row][cur_col]=2quene.append((cur_row,cur_col))fresh_nums -= 1""" 四个方向同时被腐烂 → 走完四个方向时间才会增加 """minutes += 1 return minutes if fresh_nums==0 else -13.3 带权图
(1)399 除法求值
本质上是带权有向图路径查找。
实现方案:
1. 构建图:使用字典,key为节点,value为另一个字典(邻居和对应的权重)。
2. 对于每个查询,在图中搜索路径,并计算乘积。
3. 如果路径不存在或者节点不在图中,返回-1.0。
BFS方案:
from collections import deque
from collections import defaultdict
class Solution(object):def calcEquation(self, equations, values, queries):""":type equations: List[List[str]]:type values: List[float]:type queries: List[List[str]]:rtype: List[float]"""""" step1:构建带权有向图 """graph = defaultdict(dict)node = set()for (a,b),val in zip(equations, values):graph[a][b]=valgraph[b][a]=1.0 / valnode.add(a)node.add(b)""" step2:处理每个查询 """result=[]for i,j in queries:""" 情况1-未定义查询变量 """ if i not in node or j not in node:result.append(-1.0)""" 跳过当前查询的后续处理,继续下一个查询 """continue""" 情况2-相同查询变量 """if i==j:result.append(1.0)continue""" 情况3-需要按路径查找的查询变量 """quene=deque() ## BFS队列:(当前节点, 累积乘积) visited=set() ## 记录已访问节点quene.append((i,1.0))visited.add(i)found=False ## 标记是否找到路径while quene and not found: ## 有节点待处理且未找到路径cur_node, cur_product = quene.popleft()for neighbor, value in graph[cur_node].items():""" 情况3-1:找到目标节点对应的路径 """if neighbor==j: result.append(cur_product*value)found=True""" 跳出当前邻居循环,不需要再找其他邻居了 """break""" 情况3-2:还没找到目标节点,但还有邻居没访问"""if neighbor not in visited:visited.add(neighbor)quene.append((neighbor,cur_product*value))""" 情况4:遍历完还没找到路径 """if not found:result.append(-1.0)return resultDFS方案:
from collections import deque
from collections import defaultdict
class Solution(object):def calcEquation(self, equations, values, queries):""":type equations: List[List[str]]:type values: List[float]:type queries: List[List[str]]:rtype: List[float]"""graph = defaultdict(dict)nodes = set()for (a,b),val in zip(equations, values):graph[a][b]=valgraph[b][a]=1.0/valnodes.add(a)nodes.add(b)def dfs(i, j, product, visited):""" 递归终止条件:找到目标节点,返回乘积和 """if i==j:return product""" 若还没找到目标节点 """visited.add(i) ## # 标记当前节点已访问for neighbor,value in graph[i].items():if neighbor not in visited: ## 跳过已访问节点# 递归搜索:累积路径乘积result = dfs(neighbor,j,product*value,visited)# 如果在当前路径中找到解,直接返回结果if result != -1.0:return result""" 没找到目标路径 """return -1.0result=[]for i,j in queries:if i not in nodes or j not in nodes:result.append(-1.0)elif i==j:result.append(1.0)else:visited=set() ## 每次查询都要创建新的visited集合result.append(dfs(i,j,1.0,visited))return result3.4 拓扑排序
(1)207 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
核心是判断有向图 是否存在环。给定课程的先修关系(prerequisites),构建一个有向图:
节点:每门课程 (0 到 numCourses-1)
边:
prerequisites[i] = [a, b]表示b → a(先修 b 才能学 a)需要检测这个有向图是否是 有向无环图(DAG)。
如果可以完成所有课程学习,则图无环;如果存在环则无法完成。
BFS方案:Kahn算法,根据节点的入度判断
1. 初始化:
(1)构建 邻接表 表示图(2)维护 节点入度数组(前驱课程数)
2. 入队入度为零节点:不需要先修课程即可学习的课程入队
3. BFS处理:
(1)每次出队一门课程,标记为已学,并将该课程所有后续课程的入度减1
(2)若某课程入度为零,则入队
4. 结果判断:
成功学习的课程数等于总课程数 → 可行,否则存在循环依赖 → 不可行
from collections import deque, defaultdict
class Solution(object):def canFinish(self, numCourses, prerequisites):""":type numCourses: int:type prerequisites: List[List[int]]:rtype: bool"""""" step1:构建有向图(邻接表形式)+计算节点入度 """graph = defaultdict(list)indegree = [0] * numCoursesfor course, pre_course in prerequisites:graph[pre_course].append(course) # 边:pre_course → courseindegree[course] += 1 # course入度+1(course先修课+1)""" step2:初始化队列,入度为0的course入队 """quene=deque()for i in range(numCourses):if indegree[i]==0:quene.append(i)""" step3:BFS处理 """visited = 0 ## 标记已学习的课程数while quene:cur_course=quene.popleft() ## 当前可学的课程visited+=1 for neighbor in graph[cur_course]: indegree[neighbor]-=1 ## 当前课程的后置课程入度-1if indegree[neighbor]==0:quene.append(neighbor) ## 入度为0就能开始学了return visited == numCoursesDFS方案:检测是否有环
1. 状态标记:
0=未访问,1=访问中,2=已访问2. DFS递归:
(1)进入节点时标记为"访问中"
(2)递归处理所有邻居
(3)若遇到"访问中"节点 → 发现环
(4)若所有邻居无环,回溯标记"已访问"
3. 全局检测:
为每个未访问节点启动DFS,任一环则返回不可行
""" step1:构建图 """graph = defaultdict(list)for course, pre_course in prerequisites:graph[pre_course].append(course)""" step2:DFS检测环 0: 未访问(还未进行DFS)1: 访问中(当前DFS路径中正在访问该节点)2: 已访问(该节点的DFS已经完成,没有发现环,是安全节点)"""visited = [0]*numCourses def find_circle(course):""" 递归终止条件 """if visited[course]==1: return True ## 已在当前DFS路径中 → 发现环!if visited[course]==2: return False ## 已经是安全节点 → 无需重复检查visited[course]=1 ## 标记当前节点为"访问中"(1)""" 递归检测所有后续课程 """for neighbor in graph[course]:if find_circle(neighbor):return True""" 回溯标记:将当前节点设为"安全节点"(2) """visited[course] = 2return Falsefor i in range(numCourses):if visited[i]==0: ## 每次只需要处理还没访问过的节点if find_circle(i):return Falsereturn True