当前位置：首页 > news >正文

力扣（盛最多水的容器）

news 2025/8/15 7:48:59

解析 LeetCode 11. 盛最多水的容器：双指针的巧妙运用

一、题目剖析

在这里插入图片描述

（一）问题描述

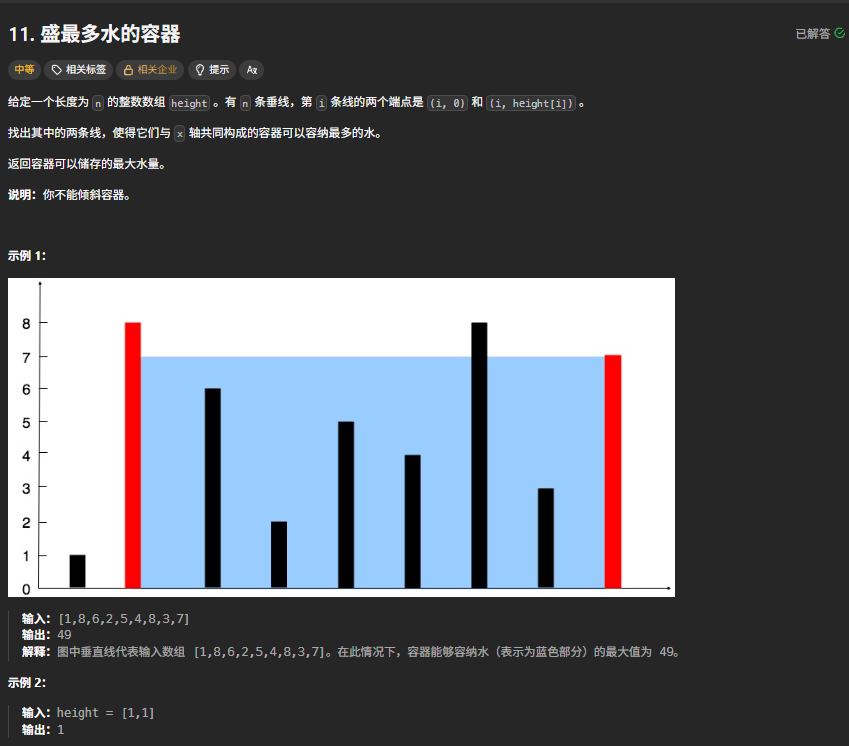
给定一个整数数组 height，数组中的每个元素代表坐标 (i, height[i]) 处垂直于 x 轴的线段高度。我们需要找出两条线段，与 x 轴构成一个容器，使得这个容器能容纳最多的水。容器的容量由较短的线段高度和两条线段在 x 轴上的距离决定，公式为：容量 = min(高1, 高2) * 水平距离 。

（二）核心挑战

如何高效地遍历所有可能的线段组合，找到容量最大的那个，同时避免暴力枚举带来的高时间复杂度。如果采用暴力法，遍历所有两两组合，时间复杂度会达到 $O(n^2)$ ，当 n 较大时，效率极低。所以需要更聪明的算法来优化。

二、算法思想：双指针的高效遍历

（一）双指针的选择逻辑

我们使用两个指针，分别从数组的两端开始（left 指向开头，right 指向末尾）。这样，初始时水平距离是最大的（为 n - 1 ，n 是数组长度）。接下来，通过移动指针来缩小范围，寻找更大的容量。

（二）指针移动的策略

容器的容量由较短的线段决定。因此：

当 height[left] < height[right] 时，说明当前容器的容量受限于 left 对应的线段高度。如果我们移动 right 指针（即选择更短的水平距离），由于 left 不变且是较短的一方，新的容量只会更小（因为水平距离减小，而高度由 left 决定，不会增加）。所以此时应移动 left 指针，尝试寻找更高的 left 线段，以期望获得更大的容量。
反之，当 height[right] <= height[left] 时，移动 right 指针，寻找更高的 right 线段，尝试提升容量。

这种指针移动策略，每次都舍弃“不可能带来更大容量”的那一侧，从而将时间复杂度优化到 $O (n)$ ，只需遍历一次数组就能找到最大容量。

三、代码实现与深度解析

class Solution {public int maxArea(int[] height) {// 初始化左指针，指向数组开头int left = 0; // 初始化右指针，指向数组末尾int right = height.length - 1; // 存储最大容量，初始为 0int max = 0; // 双指针遍历，直到左指针超过右指针while (left < right) { // 计算当前容器的容量：短边高度 * 水平距离int currArea = Math.min(height[right], height[left]) * (right - left); // 更新最大容量max = Math.max(max, currArea); // 移动指针：哪边高度低，就移动哪边的指针，寻找更高的边if (height[right] > height[left]) { left++; } else { right--; }}return max; }
}

（一）代码执行流程

初始化：left 指向数组起始位置（索引 0 ），right 指向数组末尾位置（索引 height.length - 1 ），max 初始化为 0 ，用于记录最大容量。
双指针遍历：进入 while 循环，只要 left < right ，就持续计算和比较：
- 计算当前 left 和 right 对应的容器容量 currArea ，依据是短边高度乘以水平距离。
- 用 Math.max 函数，将 currArea 与 max 比较，更新 max 为较大值。
- 根据 left 和 right 对应线段的高度，移动指针：若 height[right] > height[left] ，说明 left 是短边，移动 left 指针（left++ ）；否则移动 right 指针（right-- ）。
返回结果：循环结束后，max 中存储的就是能盛最多水的容器容量，返回 max 。

（二）关键逻辑拆解

容量计算：Math.min(height[right], height[left]) 确定短边高度，(right - left) 是水平距离，两者相乘得到当前容器容量，这是容器容量计算的核心公式。
指针移动决策：通过比较 height[left] 和 height[right] 的大小，决定移动哪一侧的指针。这样的决策确保了每次移动都是在尝试提升容器的容量，因为舍弃短边，去寻找更长的边，才有可能获得更大的容量。
时间复杂度优化：双指针只需遍历一次数组（O(n) ），相较于暴力法的 O(n^2) ，效率大幅提升，尤其在数组长度较大时优势明显。