算法提升之树上问题-（LCA）

今天学习的是关于LCA的相关问题，LCA是用来求解不同节点公共祖先的不错选择，同时我也会介绍关于倍增法求解LCA，通过倍增法可以让时间复杂度降低，类似于ST表的方式进行求解。

1.LCA的基本概念

2.倍增法求LCA

3.基本代码内容

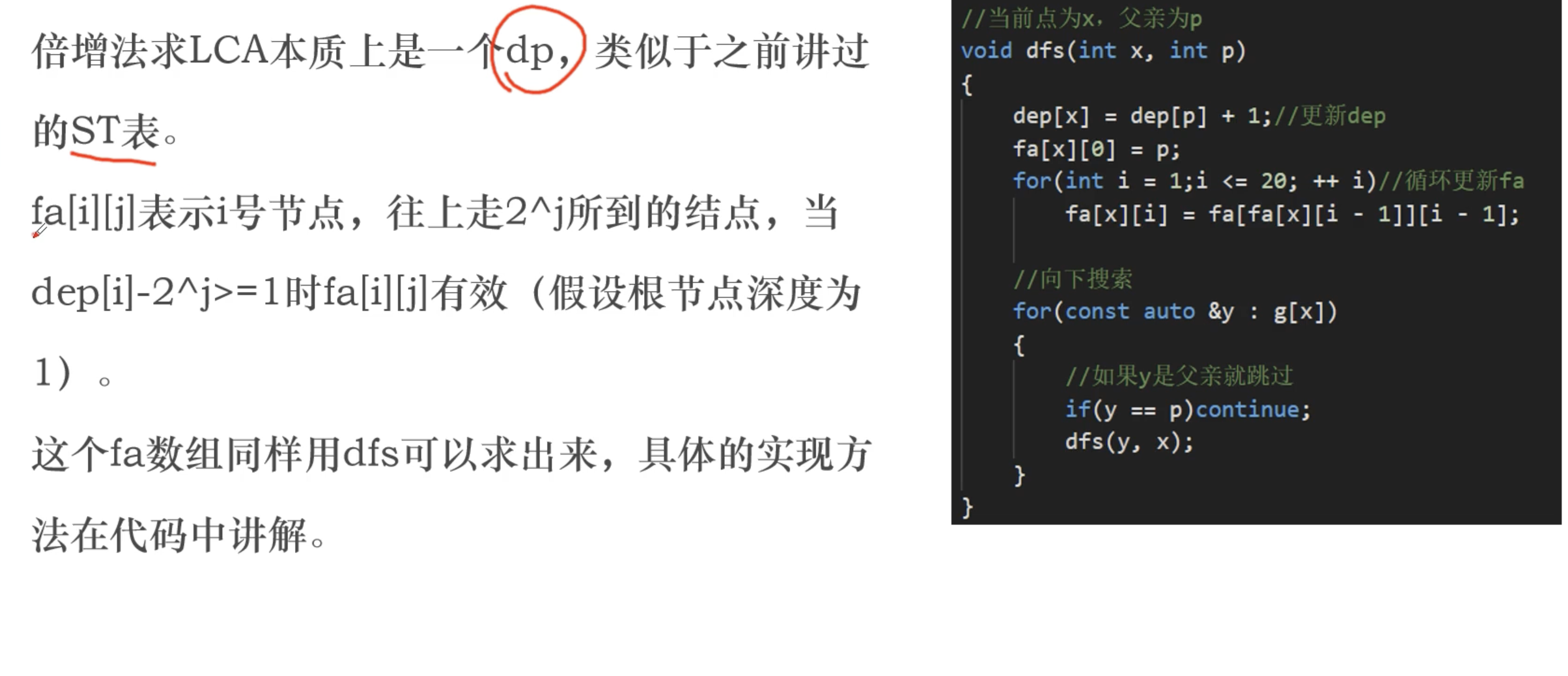
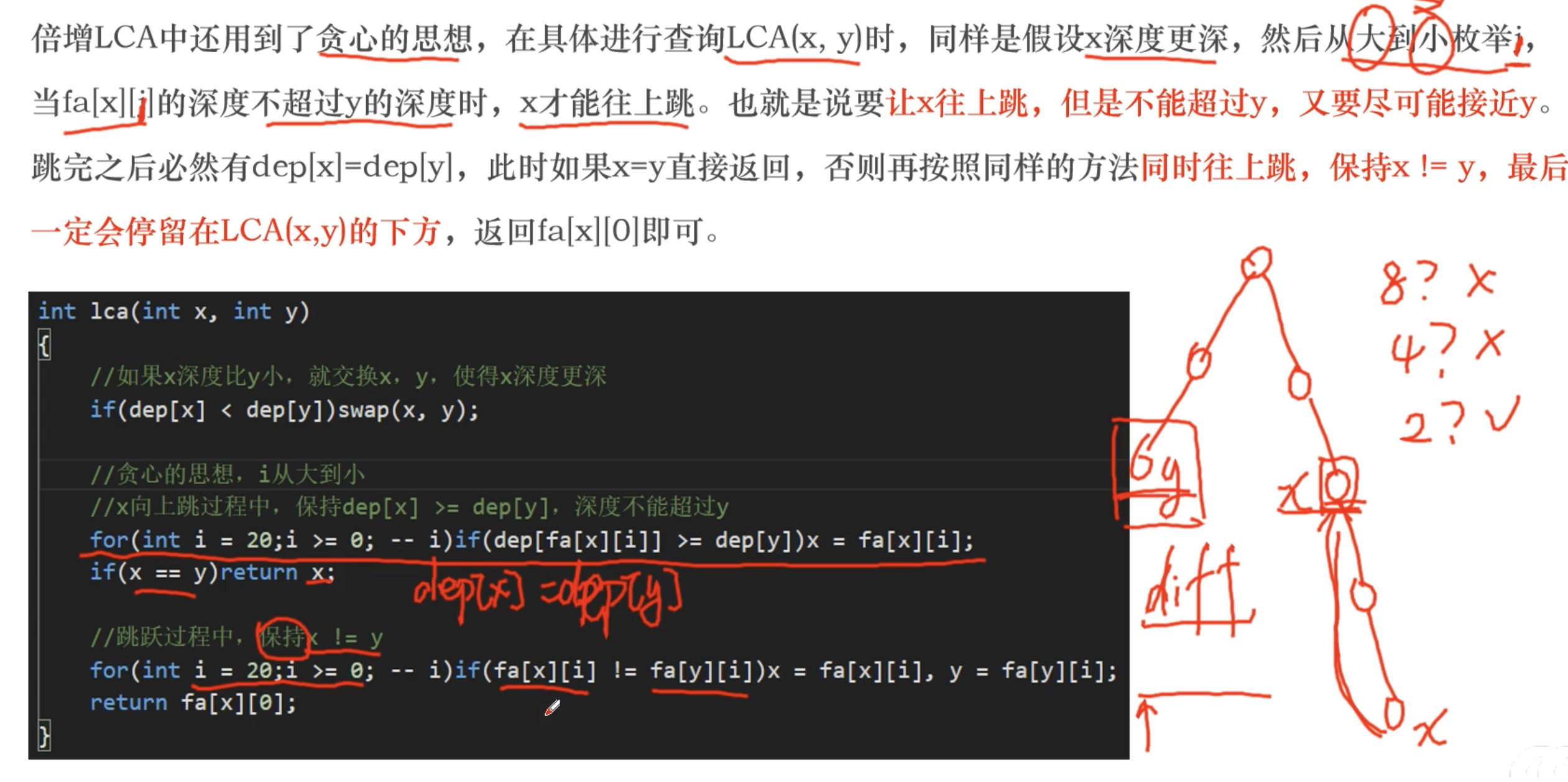
问题描述

给定一棵有 N 个节点的树，每个节点有一个唯一的编号，从 1到 N。树的根节点是 1 号节点。接下来，你会得到 Q个查询。对于每个查询，你将得到两个节点的编号，你的任务是找到这两个节点的最低公共祖先。

输入格式

第一行包含一个整数 N，表示树的节点数。

接下来的 N−1行，每行包含两个整数 U 和 V，表示节点 U和节点 V之间有一条边。

下一行包含一个整数 QQ，表示查询的数量。

接下来的 Q行，每行包含两个整数 A 和 B，表示你需要找到节点 A和节点 B的最低公共祖先

输出格式

对于每个查询，输出一行，该行包含一个整数，表示两个节点的最近公共祖先。

输入案例：

5
1 2
1 3
2 4
2 5
3
4 5
3 4
3 5

输出案例：

2
1
1

代码部分：

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5;
int n,dep[N],fa[N][21],q;
vector<int> g[N];
void dfs(int n,int p) {dep[n] = dep[p] + 1;fa[n][0] = p;for(int i = 1; i <= 20; i ++) fa[n][i] = fa[fa[n][i-1]][i-1];for(int x = 0; x < g[n].size(); x ++) {if(g[n][x] == p) continue;dfs(g[n][x],n);}
}
int lca(int x,int y) {if(dep[x] < dep[y]) swap(x,y);for(int i = 20; i >= 0; i --) if(dep[fa[x][i]] >= dep[y]) x = fa[x][i];if(x == y) return x;for(int i = 20; i >= 0; i --) if(fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];return fa[x][0];
}
int main() {cin>>n;for(int i = 1; i < n; i ++) {int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}dfs(1,1);cin>>q;while(q --) {int x,y;cin>>x>>y;cout<<lca(x,y)<<endl;}
}

这道题就是通过倍增LCA的方法求解不同字节点之间的公共节点，大家可以当作模版题去记忆，好了，今天的分享就到这里，希望对你能有所帮助。