Heterophily-aware Representation Learning on Heterogeneous Graphs

Heterophily-Aware Representation Learning on Heterogeneous Graphs （TPAMI 2025） 计算机科学 1区 I:18.6 top期刊

📌 摘要

现实世界中的图结构通常非常复杂，不仅具有全局结构上的异质性，还表现出局部邻域内的强异质相似性（heterophily）。虽然越来越多的研究揭示了图神经网络（GNN）在处理同质图中异质相似性时的局限性，但在异质图中研究异质相似性的工作仍然非常有限。

为填补这一研究空白，本文基于元路径（metapaths）对异质图中的异质相似性进行了定义，并提出了两个实用的度量指标来定量描述异质相似性的程度。通过对真实异质图的实证分析，作者发现现有的异质图神经网络（HGNN）——通常继承自同质图中的GNN机制——在面对具有异质相似性或低同质性的异质图时难以泛化。

为应对这一挑战，作者提出了一种新方法 HETERO2NET，该模型是一种面向异质图中异质相似性的HGNN。它结合了 遮蔽元路径预测（masked metapath prediction） 和 遮蔽标签预测（masked label prediction） 两项任务，能够灵活高效地处理同质性和异质性共存的图结构。

在五个具有不同异质相似性水平的真实世界异质图上进行的实验表明，HETERO2NET 在半监督节点分类任务中表现优异，超过了多种强大基线方法。特别是，该模型还能扩展至具有1300万节点和1.57亿边的工业级商业图，展示出处理大规模复杂异质图的能力。

Index Terms—Heterogeneous Graphs, Heterogeneous Graph Neural Networks, Homophily and Heterophily

1 引言

图结构在现实世界的应用中变得日益普遍，因为它们能够建模各种领域中复杂的关系和互联结构。借助这一趋势，图神经网络（GNN） 迅速发展，成为分析图结构数据的强大工具，并在众多图学习任务中达到了最先进的性能 [1]–[4]。近年来，研究人员开始积极探索 GNN 在处理异质图（heterogeneous graphs）方面的潜力。异质图也被称为异构信息网络（heterogeneous information networks），它们的特点是由多种类型的节点和边构成，每个节点或边代表不同类型的实体或关系。这种节点和边类型的多样性给异质图中的语义挖掘带来了巨大挑战——不仅要理解每种节点的语义，还要解析不同类型节点之间丰富而复杂的关系。

为应对异质性的挑战，研究者提出了大量异质图神经网络（HGNNs），用于解决与异质图相关的任务，如异质节点分类、链接预测和推荐系统等 [8], [9]。HGNN 是 GNN 在异质图场景下的扩展，能够联合学习图的结构信息和语义信息。HGNN 的研究大致可分为两类：

• 一类方法通过 定义并利用元路径（meta-paths） 来建模异质结构 [5], [8], [10], [11]；
• 另一类方法则属于 无元路径范式（metapath-free paradigms），这类方法像传统 GNN 一样从节点的局部邻域中聚合信息，但引入额外的模块将节点类型和边类型等语义信息嵌入到消息传播过程中 [6], [7], [12]–[14]。

尽管 GNN 和 HGNN 已取得了显著成功，越来越多的研究文献 [15], [15]–[20] 也揭示了一个重要的局限性：常规 GNN 在处理异质相似性（heterophily）较强的图时表现较差，特别是在同质图中，当相连节点拥有不同的标签和/或属性时（即“异性相吸”原则）。虽然现有的 HGNN 在设计上继承了许多原本为同质图开发的 GNN 机制，但目前尚不清楚 HGNN 是否能够有效处理具有异质相似性的异质图——这一问题在现有文献中尚未被明确定义和深入研究。

为弥补这一研究空白，本文旨在通过引入基于元路径（metapaths）的异质图中异质相似性（heterophily）定义，为该方向建立一个新的研究基础。元路径本身是异质图中一个定义良好的概念 [5], [8]。
如图 1 所示，作者指出异质图学习中面临的三大核心挑战：

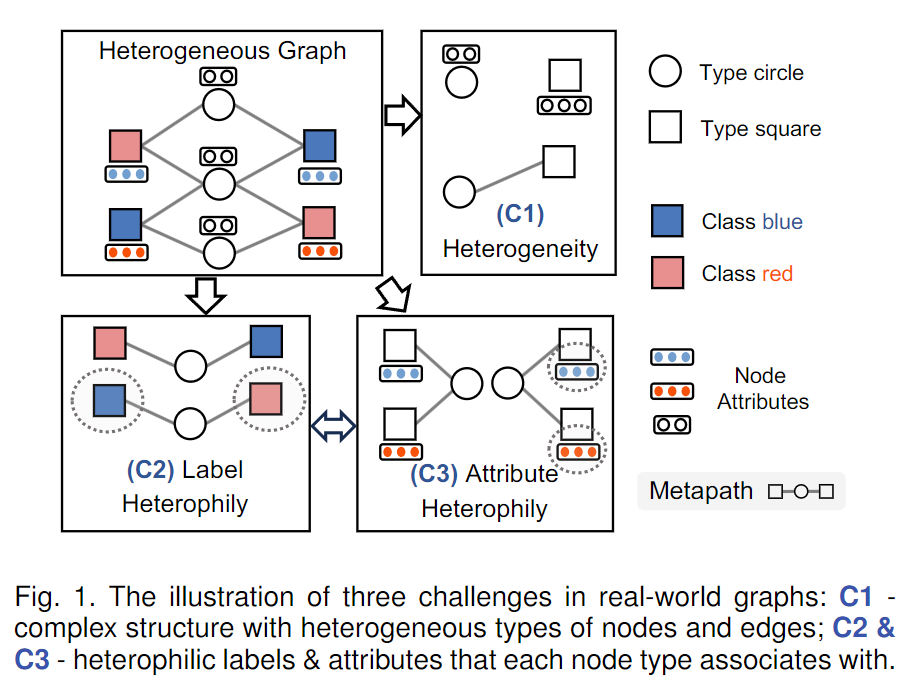
1. 图的异质性（heterogeneity），
2. 标签异质相似性（label heterophily），
3. 属性异质相似性（attribute heterophily）。

在这里，异质相似性指的是：两个相同类型的节点通过元路径相连，但它们在标签或属性上存在差异。

为了量化异质相似性的程度，作者提出了两个实用的度量指标：

• 基于元路径的标签同质性（MLH）：将传统的同质性比率 [16] 从同质图扩展到了异质图；
• 基于元路径的 Dirichlet 能量（MDE）：衡量局部邻域中特征的平滑性。

通过实证研究，作者发现：在 MLH 和 MDE 指标下，当前的 HGNN 模型在异质图中难以泛化到异质相似性较强（或同质性较低/中等）的场景。在这类场景下，甚至一些完全不利用图结构的模型（如多层感知机 MLP）在许多情况下都优于 HGNN，这一发现进一步凸显了现有方法的局限性。

针对上述挑战，本文提出了一种新颖的异质图神经网络模型 HETERO2NET，它具备异质相似性感知能力，能够同时应对在标签或属性层面具有 同质性（homophily）或异质性（heterophily） 的异质图。在技术上，HETERO2NET 引入了 遮蔽元路径预测（masked metapath prediction） 机制，分别学习解耦的同质性与异质性表示。这两类表示能够捕捉图中不同的属性信号，从而有助于下游任务的执行。此外，HETERO2NET 还引入了 遮蔽标签预测（masked label prediction） 策略，以增强节点之间的消息传播，特别是对于那些表现出强标签异质性的节点。这两种设计分别有助于解决属性异质性和标签异质性带来的挑战。

我们的主要贡献如下：

• 异质相似性度量与现有方法的局限性：我们提出了两个基于元路径的异质相似性度量指标 —— MLH（标签同质性） 和 MDE（属性Dirichlet能量），分别用于衡量异质图中的标签异质性和属性异质性。通过实证研究，我们揭示了现有 HGNN 在处理具有异质相似性的异质图时的显著局限性，而这一问题在现有文献中长期被忽视，其根本原因是缺乏明确的异质性度量方法。

• 面向异质相似性的全新模型：基于上述挑战，我们提出了 HETERO2NET —— 一个新颖的、具有异质相似性感知能力的 HGNN。该模型通过引入解耦的遮蔽图预测任务和遮蔽标签预测任务，能够灵活高效地处理同质性与异质性共存的异质图（其技术细节如图 2 所示）。

• 大规模实证验证：我们在五个真实世界的异质图数据集上进行了实验评估，包括一个包含 1300 万节点和 1.57 亿边的工业级商业图。实验结果表明，HETERO2NET 在半监督节点分类任务中表现优越，在性能和可扩展性方面均优于多种强基线方法。

论文结构安排：

本文其余部分的结构安排如下：

• 第 2 部分 回顾了与本研究相关的已有工作；
• 第 3 部分 介绍了基本符号和必要的预备知识；
• 第 4 部分 提出了两个基于元路径的异质相似性度量指标，并进行了关于不同异质性水平异质图的实证研究；
• 第 5 部分 详细介绍了我们提出的 HETERO2NET 框架，包括解耦的遮蔽元路径预测和遮蔽标签预测两项关键技术；
• 第 6 部分 展示了实验结果；
• 最后，第 7 部分 总结了全文，并展望了异质图学习在更广泛场景中的未来研究方向。

2 相关工作

本节回顾与本研究密切相关的文献，主要包括以下两个方面的研究进展：

• 异质图神经网络（Heterogeneous Graph Neural Networks, HGNNs）；
• 在异质相似性图上进行的图表示学习（Graph Representation Learning over Heterophilic Graphs）。

2.1 异质图神经网络（Heterogeneous Graph Neural Networks, HGNNs）

近年来，为了满足对高效建模各种异质图日益增长的需求，出现了大量关于 HGNN 的研究工作 [24]。
根据处理图中语义信息的方式不同，HGNN 大致可以分为两类：基于元路径的方法 和 非元路径的方法。

• 基于元路径的 HGNN 通过手工设计或自动选择的元路径进行邻居特征的传播与聚合。
  例如：
  • Metapath2Vec [8] 使用元路径引导的随机游走，捕捉异质节点之间的语义信息；
  • GTN [25] 为不同元路径分配可学习的权重，从而自动学习有用的元路径；
  • HAN [5] 引入层次注意力机制，分别建模节点层级和语义层级的结构；
  • 作为后续工作，MAGNN [11] 在 HAN 的基础上引入了元路径聚合机制，以从多个元路径中学习语义信息。

非元路径的 HGNN 方法将传统 GNN 中的消息传递与聚合机制扩展到异质图上，无需手动设计有意义的元路径。

例如：

• RGCN [12] 及其后续工作 RGAT [26] 提出针对每种边类型提取关系特定的模式，然后将不同语义信息进行融合；
• SHGN [7] 引入了多层图注意力网络，并在边注意力机制中加入可学习的边类型嵌入；
• HGSL [27] 通过挖掘复杂交互关系，联合学习异质图结构和 GNN 参数；
• 受到 Transformer [28] 成功经验的启发，HGT [6] 和 HINormer [22] 将自注意力机制引入图结构的消息传递中，用于建模异质节点之间的结构依赖关系。

2.2 异质相似性图上的学习

异质相似性图（heterophilic graphs）是指：相连节点更可能具有不同的属性或标签。近年来，这一类图结构受到了研究界越来越多的关注 [15], [15]–[20]。异质相似性问题为图分析与建模带来了独特挑战。

• Pei 等人 [16] 首次关注到这一现象，并提出了一种度量图的同质性水平的指标；
• Zhu 等人 [15] 随后深入研究了 GNN 在异质或非同质图上性能下降的问题，并提出了 H2GCN，以在存在异质相似性的情况下改进图结构的学习；
• CPGNN [17] 通过引入兼容性矩阵（compatibility matrix），将 GNN 泛化为同时支持同质性与异质性的图；
• FAGCN [18] 在消息传递过程中引入了一种自适应整合机制，可动态融合低频与高频信号；
• LINKX [15] 关注如何将 GNN 扩展到大规模异质图，通过 MLP 学习和融合特征矩阵与邻接矩阵的信息；
• Luan 等人 [23] 从后聚合节点相似性的角度分析异质性，并提出了一种多通道混合机制，以提取丰富的本地信息，适应不同形式的节点异质相似性。

然而，大多数现有研究仍集中于同质图，对于异质图中的异质相似性问题尚缺乏深入探索。随着异质图在各类应用中的日益普及，开发能够有效处理异质相似性并应对其带来挑战的方法变得愈发重要。近期也有一些并行工作的研究开始关注在异质相似性环境下进行异质图学习 [30]–[33]。然而，这些方法普遍缺乏系统性的异质性量化指标，也缺少一个合理的框架来区分基于属性的异质性与基于标签的异质性，这正是促使我们开展本研究的动因。

3 预备知识（PRELIMINARY）

在本节中，我们将介绍与异质图相关的基本概念和符号表示，同时引入用于衡量图的同质性/异质性的度量指标。论文中经常使用的符号已在表 1中进行了汇总。

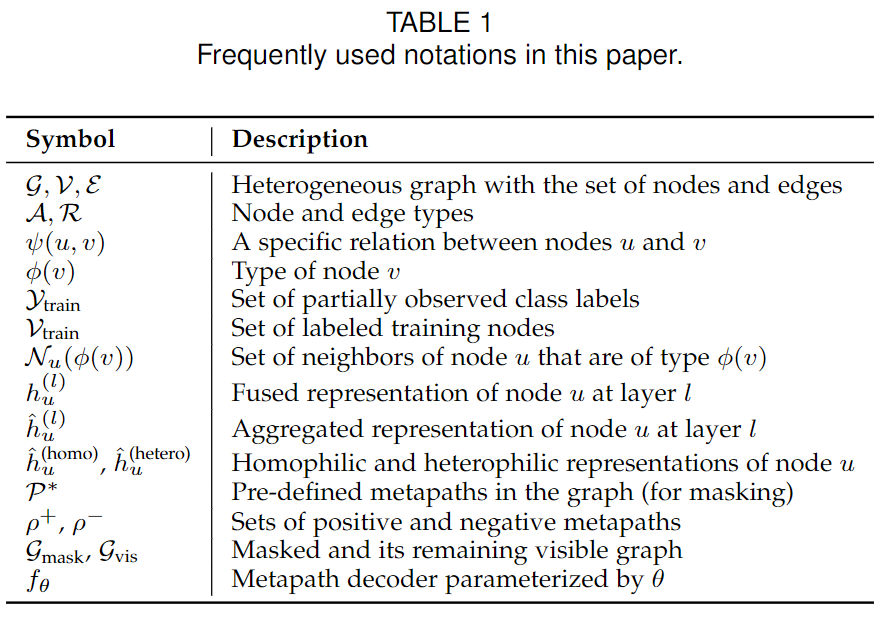
3.1 异质图（Heterogeneous Graphs）

一个异质图或称为异构信息网络，定义为：G={ V,E,A,R,φ,ψ}G = \{V, E, A, R, \varphi, \psi\}G={ V,E,A,R,φ,ψ} 其中，$V$ 和 $E$ 分别表示节点集合和边集合。

该图还包括：

• 一个节点类型映射函数 $\phi :V\to A$，用于将每个节点映射为其对应的类型；
• 一个边类型映射函数 $\psi :E\to R$，用于将每条边映射为其对应的关系类型（边类型）；
• 其中，$A$ 表示所有可能的节点类型集合，$R$ 表示所有可能的关系类型集合，并且满足 $|A|+|R|>2$。当 $|A|=|R|=1$ 时，图 $G$ 就退化为一个同质图。

在大多数情况下，图 $G$ 是具备属性的，即每个节点 $u\in V$ 都关联一个 $d$-维的属性向量 $x_u\in {\mathbb{R}}^d$。
在节点分类任务中，某些节点类型或特定的节点还会被分配一个类别标签 $y$。然而，在异质图中：

• 并非所有节点类型都具备标签；
• 即使是带标签的节点类型，其内部通常也只有部分节点拥有标注信息。

3.2 异质图中的元路径（Metapath）

元路径（Metapath）：
长度为 $n$ 的元路径记作：$P\triangleq A_1\stackrel{R_1}{\to }{A}_2\stackrel{R_2}{\to }\cdots \stackrel{R_n}{\to }{A}_{n+1}$

简记为 $A_1{A}_2\cdots A_{n+1}$，其中：

• $A_i\in A$ 表示节点类型，
• <