力扣top100(day02-04)--二叉树 01
94. 二叉树的中序遍历

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {// 主方法:启动中序遍历并返回结果列表public List<Integer> inorderTraversal(TreeNode root) {// 创建结果列表,用于存储遍历结果List<Integer> res = new ArrayList<Integer>();// 调用递归辅助方法进行中序遍历inorder(root, res);// 返回遍历结果return res;}/*** 递归实现的中序遍历辅助方法* 中序遍历顺序:左子树 -> 根节点 -> 右子树* @param root 当前遍历的树节点* @param res 存储遍历结果的列表*/public void inorder(TreeNode root, List<Integer> res) {// 递归终止条件:当前节点为空if (root == null) {return;}// 1. 递归遍历左子树inorder(root.left, res);// 2. 访问当前根节点(将节点值加入结果列表)res.add(root.val);// 3. 递归遍历右子树inorder(root.right, res);}
}关键点说明
中序遍历顺序:
左子树 → 根节点 → 右子树
对于二叉搜索树(BST),中序遍历会产生一个升序序列
递归实现特点:
递归终止条件:当前节点为null时返回
递归过程:严格按照左-根-右的顺序进行递归调用
时间复杂度分析:
O(n):需要访问树中的每个节点一次
n为二叉树中的节点总数
空间复杂度分析:
最坏情况O(n):当树退化为链表时,递归栈的深度等于节点数
平均情况O(log n):平衡二叉树情况下递归栈深度
示例执行流程
对于如下二叉树:
text
1\2/3遍历过程:
访问节点1,先递归左子树(null,直接返回)
将1加入结果列表
访问节点1的右子树(节点2)
访问节点2的左子树(节点3)
访问节点3的左子树(null)
将3加入结果列表
访问节点3的右子树(null)
将2加入结果列表
访问节点2的右子树(null)
最终结果:[1, 3, 2]
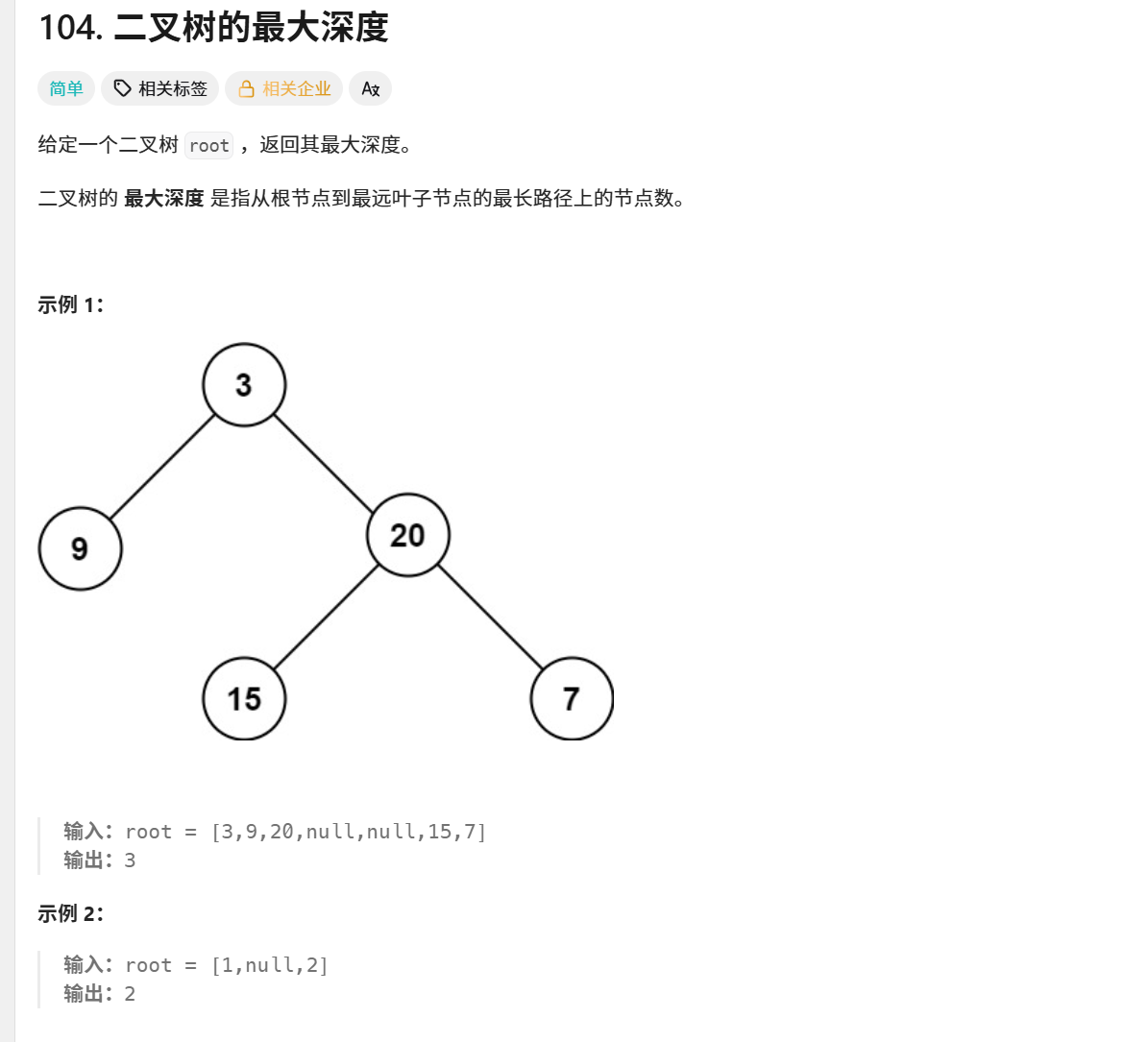
104. 二叉树的最大深度
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;} else {int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return Math.max(leftHeight, rightHeight) + 1;}}
}
关键点说明
递归思想:
一棵树的最大深度 = 左子树和右子树中较大的深度 + 1(当前节点)
这种"自顶向下"分解问题,"自底向上"计算结果的思路是典型的递归解法
递归终止条件:
当节点为null时,深度为0(这是递归的基本情况)
时间复杂度:
O(n):需要访问树中的每个节点一次
n为二叉树中的节点总数
空间复杂度:
最坏情况O(n):当树退化为链表时,递归栈的深度等于节点数
平均情况O(log n):平衡二叉树情况下递归栈深度
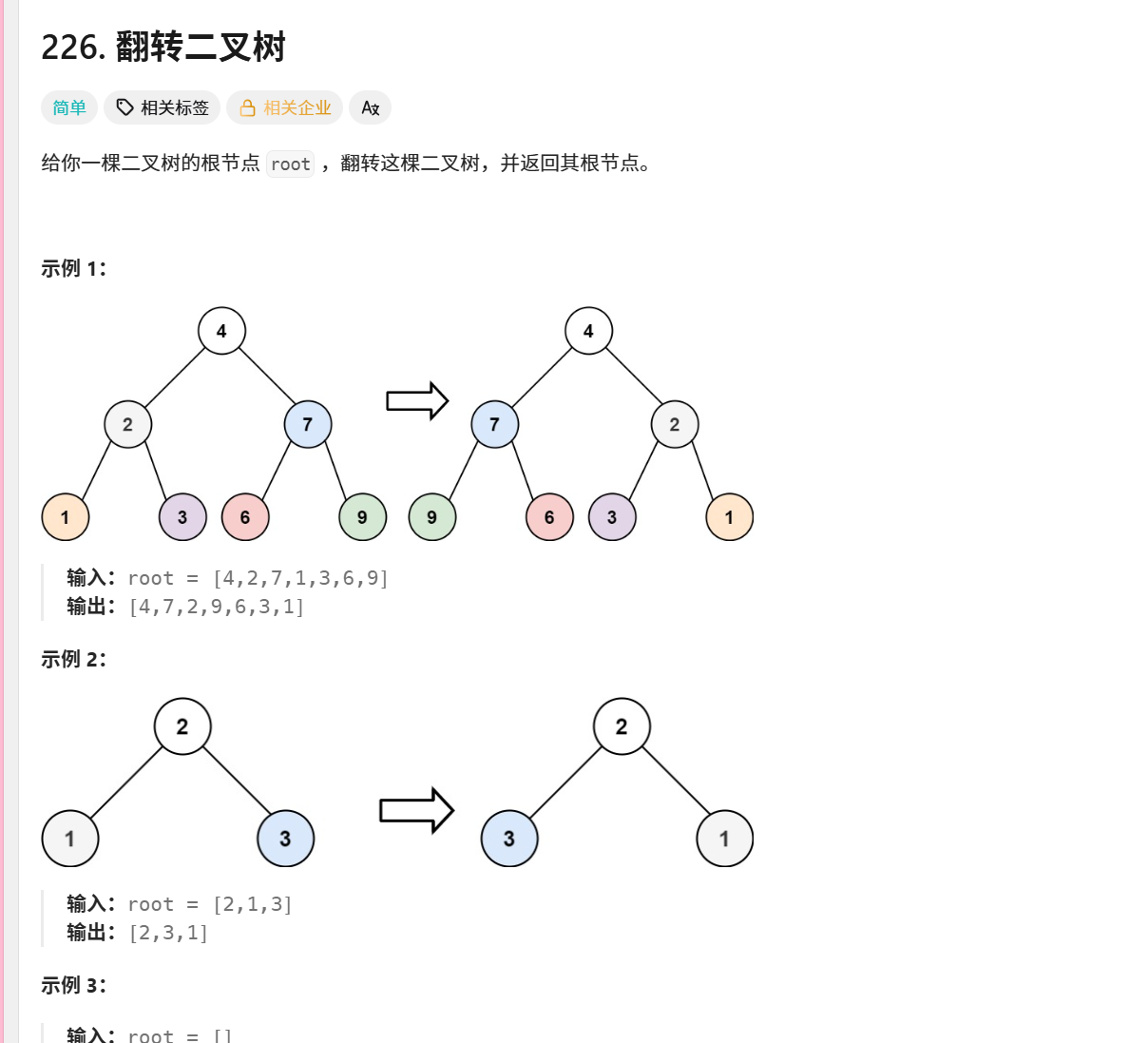
226. 翻转二叉树

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}TreeNode left = invertTree(root.left);TreeNode right = invertTree(root.right);root.left = right;root.right = left;return root;}
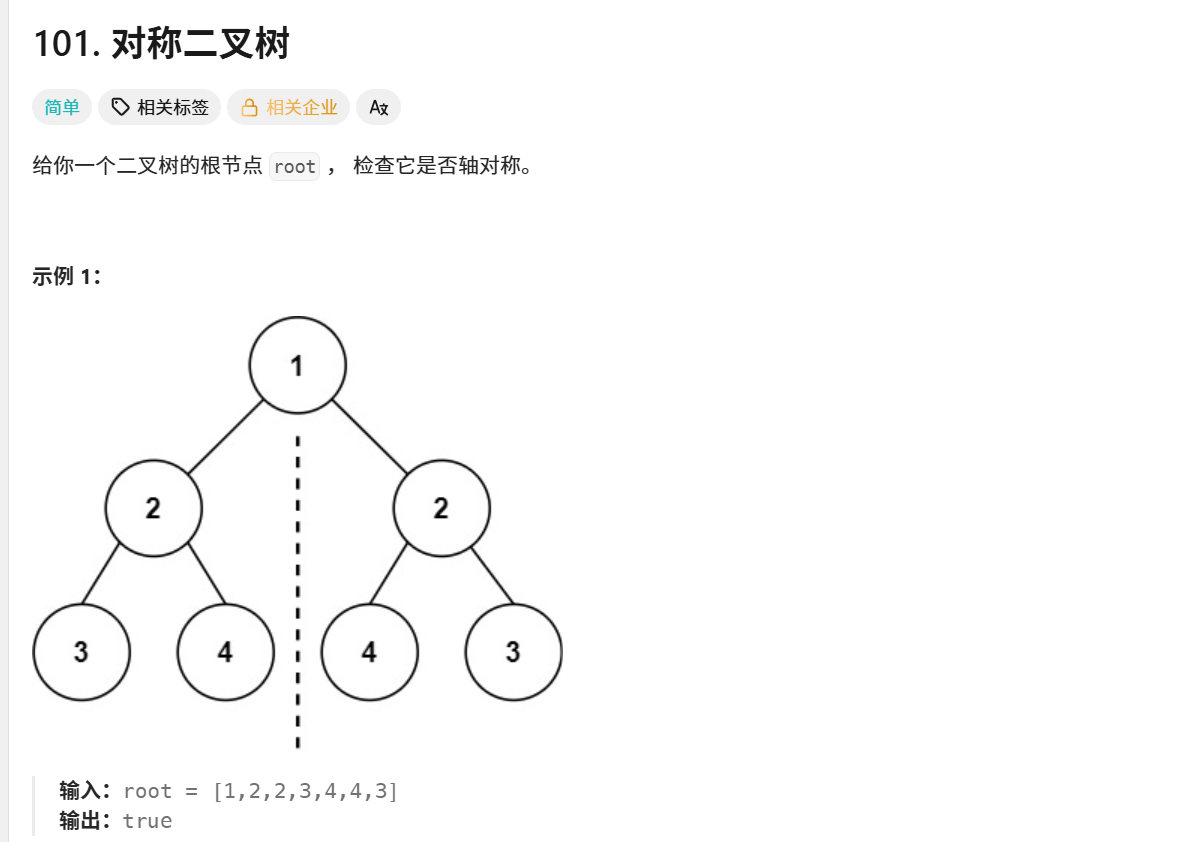
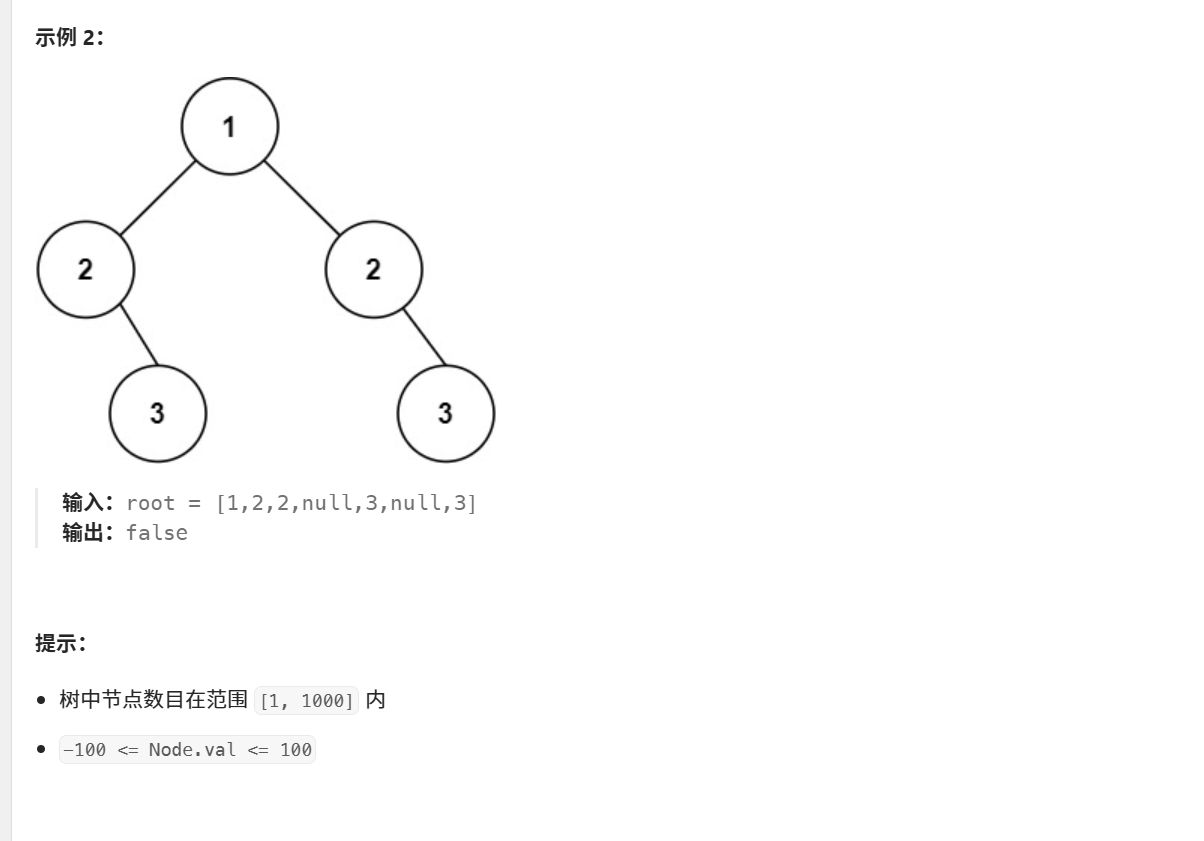
}101. 对称二叉树
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return check(root.left, root.right);}public boolean check(TreeNode p, TreeNode q) {if (p == null && q == null) {return true;}if (p == null || q == null) {return false;}return p.val == q.val && check(p.left, q.right) && check(p.right, q.left);}
}543. 二叉树的直径

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {int ans;public int diameterOfBinaryTree(TreeNode root) {ans = 1;depth(root);return ans - 1;}public int depth(TreeNode node) {if (node == null) {return 0; // 访问到空节点了,返回0}int L = depth(node.left); // 左儿子为根的子树的深度int R = depth(node.right); // 右儿子为根的子树的深度ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ansreturn Math.max(L, R) + 1; // 返回该节点为根的子树的深度}
}关键点说明
直径定义:
二叉树的直径是任意两个节点间最长路径的长度(边数)
这个路径不一定经过根节点
算法思路:
对于每个节点,计算通过它的最长路径(左子树深度+右子树深度)
在计算深度过程中,不断更新全局最大直径
最终直径为最大节点数-1
递归过程:
depth()函数计算子树深度在计算深度时,同时计算通过当前节点的路径长度(L+R+1)
使用成员变量
ans记录全局最大值时间复杂度:
O(n):每个节点只访问一次
n为二叉树中的节点总数
空间复杂度:
最坏情况O(n):树退化为链表时递归栈深度
平均情况O(log n):平衡二叉树情况下递归栈深度
示例执行流程
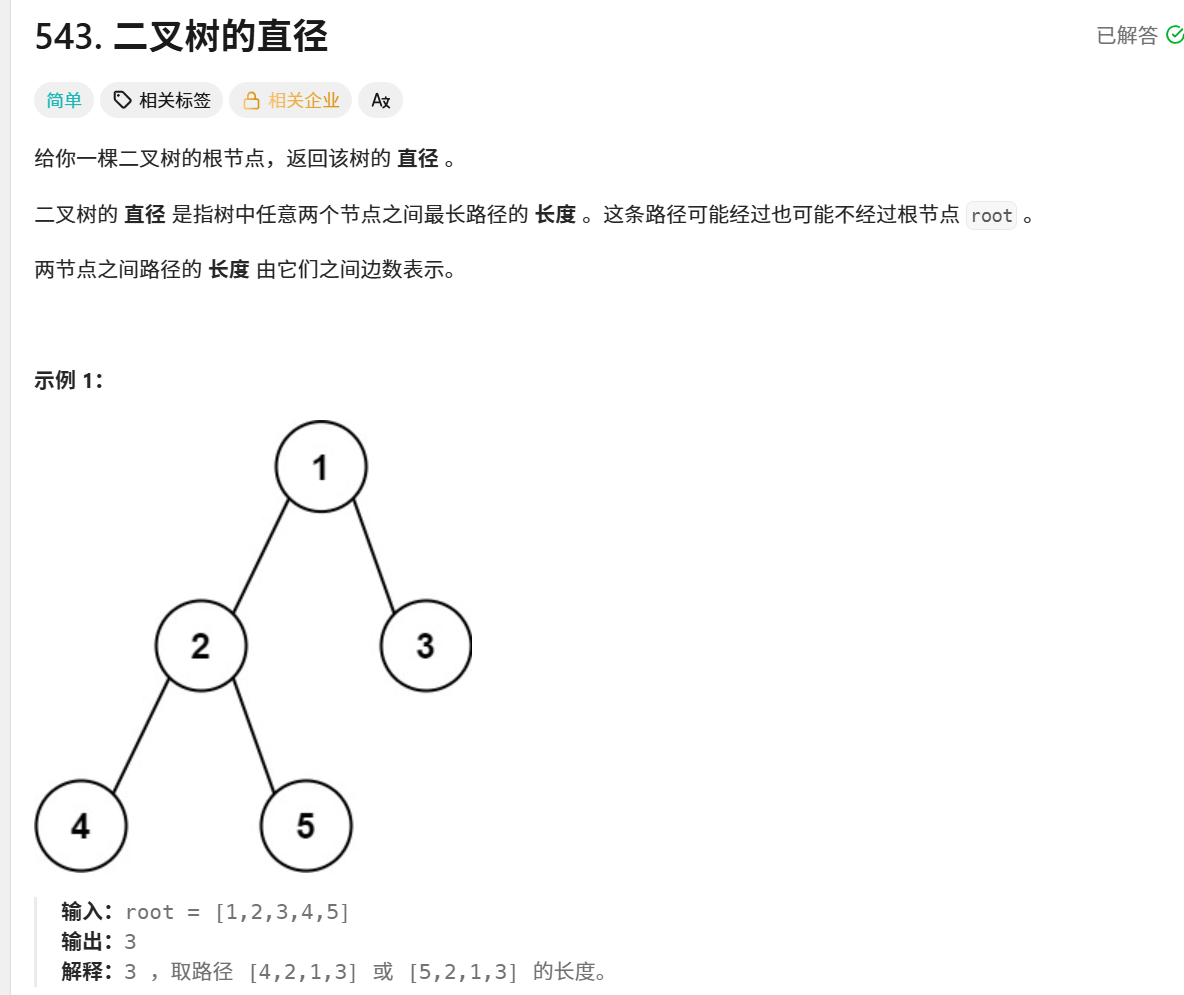
对于如下二叉树:
text
1/ \2 3/ \ 4 5计算过程:
访问节点4:L=0, R=0 → ans=max(1,1)=1 → 返回1
访问节点5:L=0, R=0 → ans=max(1,1)=1 → 返回1
访问节点2:L=1(4), R=1(5) → ans=max(1,3)=3 → 返回2
访问节点3:L=0, R=0 → ans=max(3,1)=3 → 返回1
访问节点1:L=2(2), R=1(3) → ans=max(3,4)=4 → 返回3
最终直径:ans-1=3(路径[4,2,1,3]或[5,2,1,3])
为什么这种方法有效?
最长路径必然经过某个子树的根节点
通过计算每个节点左右子树深度之和,可以找到所有可能的路径长度
在计算深度的过程中,我们实际上检查了所有可能的路径
这种递归解法巧妙地将深度计算和直径查找结合在一起,通过一次遍历即可解决问题,效率很高。
递归思想详解
递归是编程中一种非常重要的思想,它通过将大问题分解为相似的小问题来解决问题。让我们深入理解递归的核心概念和应用。
递归的基本原理
递归包含两个关键部分:
-
基准条件(Base Case):最简单的情况,可以直接得出答案
-
递归条件(Recursive Case):将问题分解为更小的同类问题
递归三要素
-
明确函数的功能:清楚知道这个函数要解决什么问题
-
寻找递归结束条件:防止无限递归
-
找出函数的等价关系式:如何通过更小的问题解决当前问题
递归在二叉树问题中的应用
以计算二叉树最大深度为例:
public int maxDepth(TreeNode root) {// 基准条件:空树的深度为0if (root == null) {return 0;}// 递归条件:当前树深度 = 左右子树中较大的深度 + 1return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
执行过程分析:
-
从根节点开始,先计算左子树深度
-
再计算右子树深度
-
取两者较大值加1得到当前树的深度
递归的优缺点
优点:
-
代码简洁清晰
-
适合处理树形结构、分治问题等
-
数学表达自然(如斐波那契数列、阶乘等)
缺点:
-
可能产生大量重复计算(如朴素斐波那契递归)
-
递归深度过大可能导致栈溢出
-
效率通常低于迭代实现
递归优化技巧
-
记忆化(Memoization):存储已计算结果避免重复计算
Map<TreeNode, Integer> memo = new HashMap<>();public int maxDepth(TreeNode root) {if (root == null) return 0;if (memo.containsKey(root)) return memo.get(root);int depth = Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;memo.put(root, depth);return depth; } -
尾递归优化:某些编译器可以优化尾递归为迭代,减少栈空间使用
-
转换为迭代:使用栈或队列模拟递归过程
经典递归问题示例
-
阶乘计算:
int factorial(int n) {if (n == 1) return 1; // 基准条件return n * factorial(n - 1); // 递归条件 } -
斐波那契数列:
int fib(int n) {if (n <= 1) return n; // 基准条件return fib(n - 1) + fib(n - 2); // 递归条件 } -
二叉树遍历(前序、中序、后序)
