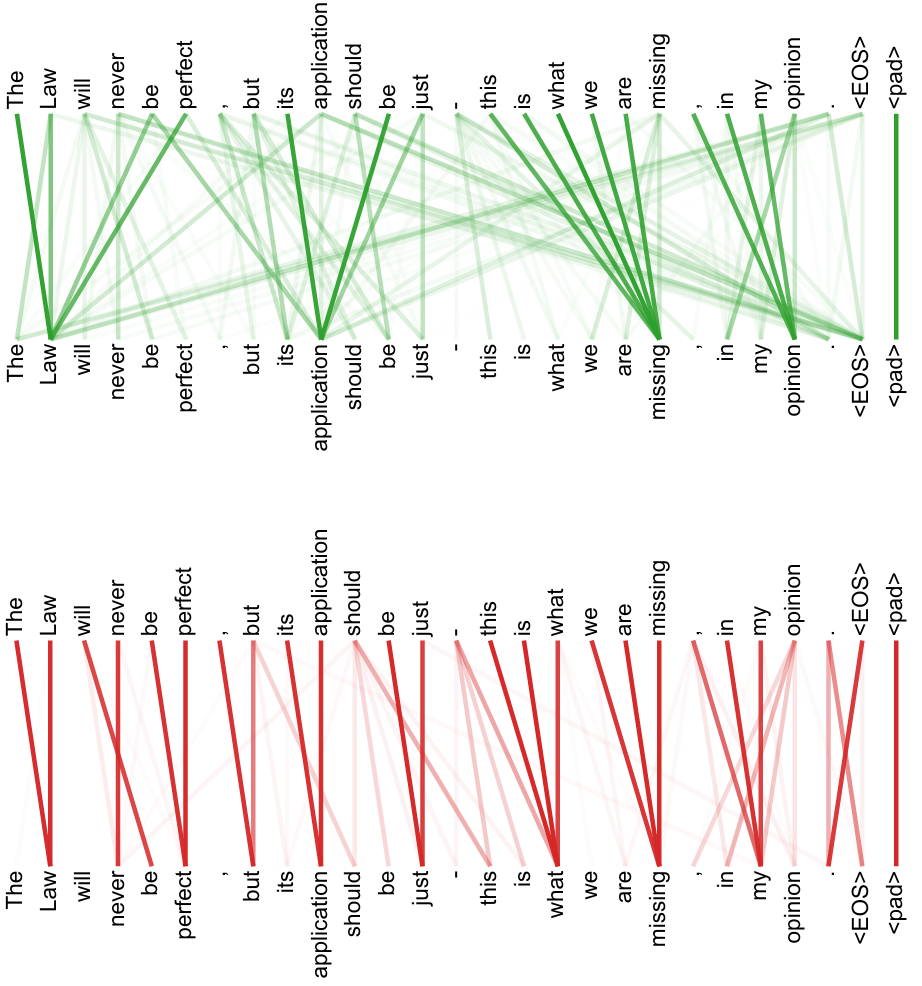
NLP学习之Transformer（1）

初识 Transformer （1）

1.简介

1.1主要特点：

self-attention：

自注意力机制，Transformer的核心是自注意力机制，它允许模型在处理某个位置的输入时，能够直接与其他位置的输入交互，而不像CNN、RNN只能顺序处理数据。自注意力机制通过计算输入序列中各位置之间的相似度来决定各位置之间的影响力，从而提高了模型的表现力。

并行化能力

由于Transformer不依赖于序列的顺序处理，它的计算过程可以并行化，这就可以显著提高了训练效率。

Encoder-Decoder

Transformer 采用了典型的编码器-解码器架构。编码器负责处理输入序列，将其转换为上下文相关的表示；解码器则根据这些表示生成输出序列。

1.2. 模型结构

Transformer主要由编码器（Encoder）和解码器（Decoder）组成，广泛应用于自然语言处理任务，尤其是机器翻译。

—

2.代码实现

2.1 输入序列

输入是一个序列，如词向量序列，假设：
$$X=(x_1,x_2,\dots ,x_n)\in {\mathbb{R}}^{n\times d}$$
是 $n$ 个输入，$d$ 是输入维度，则自注意力的目的是捕获 $n$ 个实体之间的关系。

  #定义一个词表vocab={"我","是","一个","好","人"}

2.2 词语关系

it代表的是animal还是street呢，对我们来说简单，但对机器来说是很难判断的。self-attention就能够让机器把it和animal联系起来。

2.3 线性变换

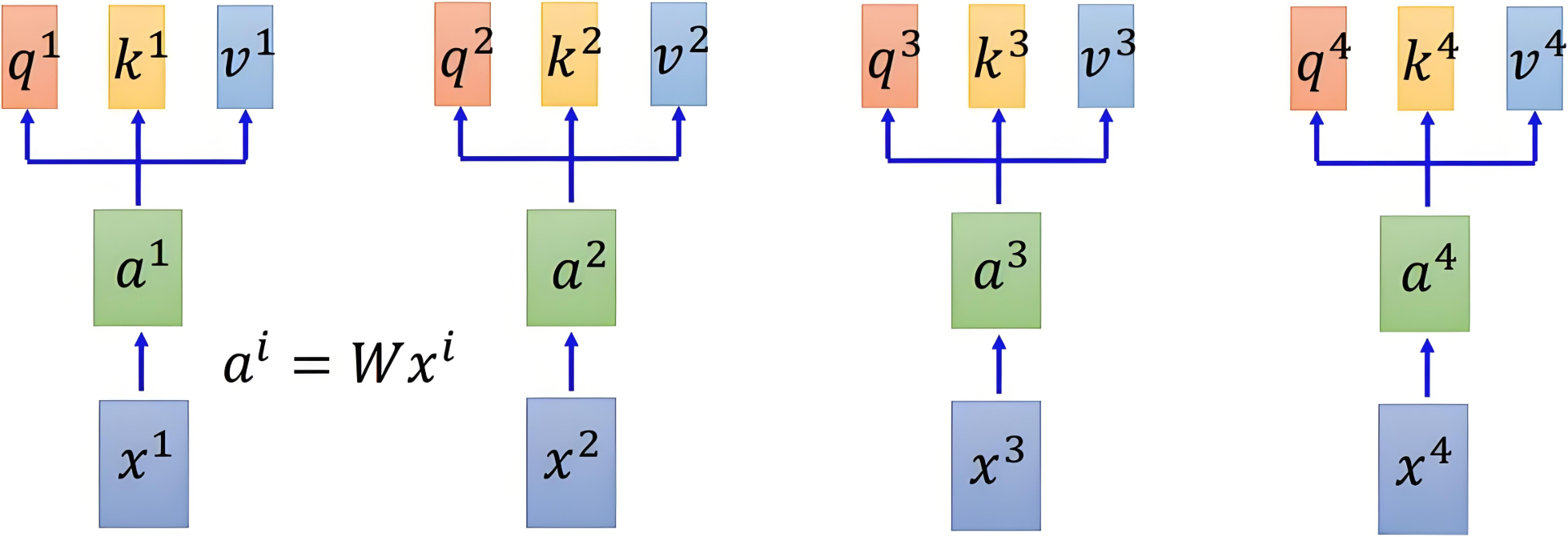
自注意力机制依赖于三个核心概念：查询向量Query、键向量Key、值向量Value。他们对输入 $X$ 进行三次线性变换，得到三个矩阵。

#词嵌入向量num_embedding=len(vocab)embedding=nn.Embdedding(num_embedding,256)#词嵌入，传入词表大小和词嵌入维度（特征维度）#获取“我的”的词向量embed=embedding(torch.Tensor([0]))#映射一个query向量Q=nn.Linear(256,4)(embed)#映射一个key向量K=nn.Linear(256,4)(embed)#映射一个value向量V=nn.Linear(256,4)(embed)

2.3.1 查询向量

Q = Query, 是自注意力机制中的“询问者”。每个输入都会生成一个查询向量，表示当前词的需求。

• 作用：用于与键向量计算相似度（通过点积方式），确定当前词与其他词的相关性。
• 生成方式：通过一个权重矩阵将输入数据（如词向量）映射到查询空间。

$$Q=X{W}_q$$

$W_q$ 是可学习权重矩阵，维度为 $d\times d_k$，$d_k$是超参数，表示查询向量的维度。

2.3.2 键向量

**K = **Key，表示其他词的信息，供查询向量匹配。每个输入都会生成一个键向量，表示其能够提供的信息内容。

• 作用：与查询向量计算点积，生成注意力权重。点积越大，表示它们之间的相关性越强。
• 生成方式：通过一个权重矩阵将输入数据（如词向量）映射到键空间。

$$K=X{W}_k$$

$W_k$ 是可学习权重矩阵，维度为 $d\times d_k$，$d_k$是超参数，表示键向量的维度。

2.3.3 值向量

V = Value, 值向量包含了每个输入实际的信息内容，相关性决定了信息被聚焦的程度。

• 作用：使用值向量基于注意力得分进行加权求和，生成最终的输出表示。
• 生成方式：通过一个权重矩阵将输入数据（如词向量）映射到值空间。

$$V=X{W}_v$$

$W_v$ 是可学习权重矩阵，维度为 $d\times d_v$，$d_v$是超参数，表示值向量的维度。

2.3.4 以图示意

通过线性变换得到三个向量的变化如下图所示：

2.4 注意力得分

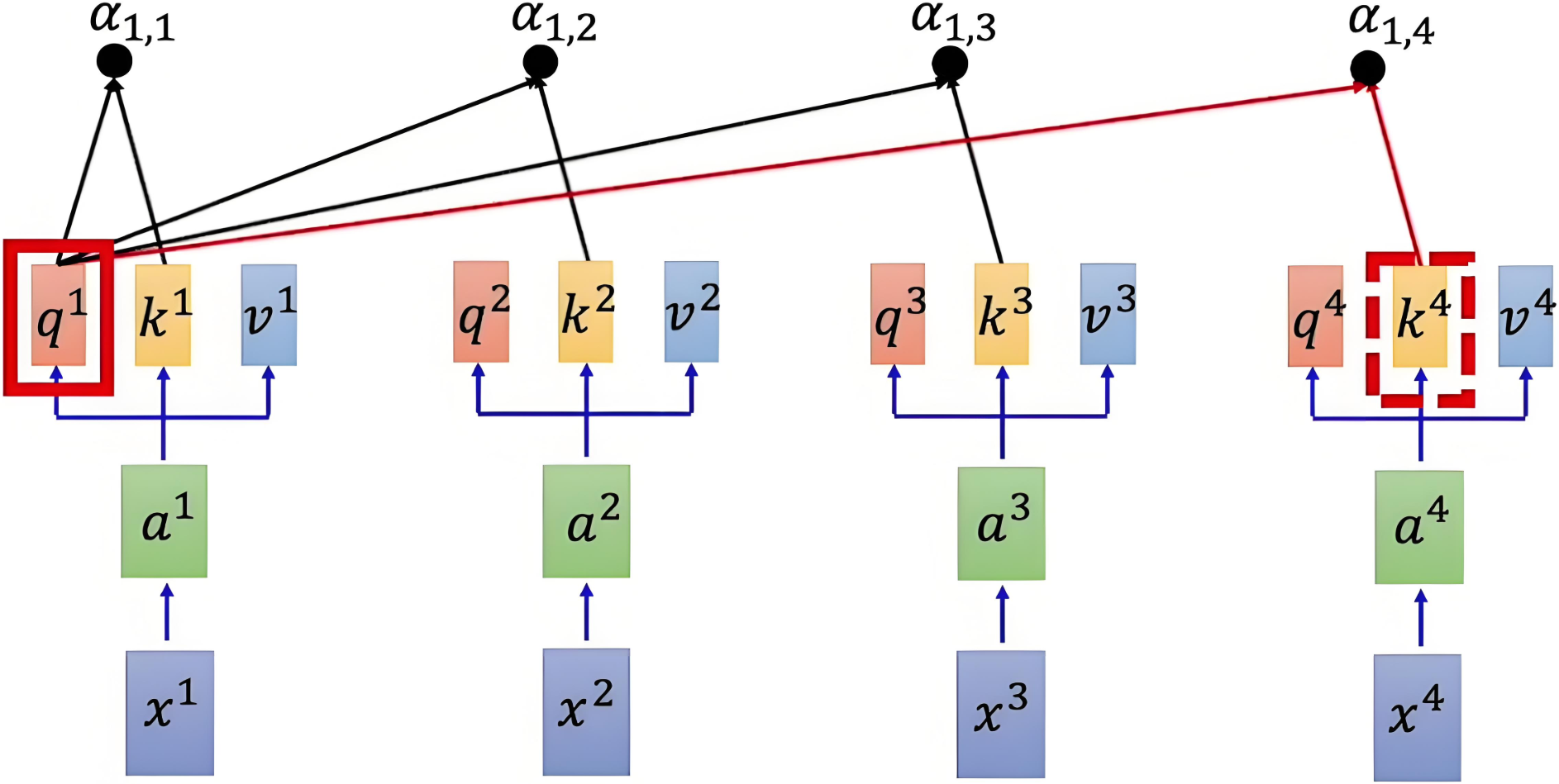
使用点积来计算查询向量和键向量之间的相似度，除以缩放因子 $\sqrt{d_k}$ 来避免数值过大，使得梯度稳定更新。得到注意力得分矩阵：
$$\text{Attention}(Q,K)=\frac{Q{K}^T}{\sqrt{d_k}}$$
注意力得分矩阵维度是 $n\times n$，其中 $n$ 是序列的长度。每个元素 $(i,j)$ 表示第 $i$ 个元素与第 $j$ 个元素之间的相似度。

参考示意图如下：

   fc = nn.ModuleList(nn.Linear(dim, dim) for _ in range(3))Q = fc[0](sentence_embedding)K = fc[1](sentence_embedding)V = fc[2](sentence_embedding)# print(Q.shape, K.shape, V.shape)# 余弦相似度  []# "I Love Nature Language Processing"sim = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(dim)# print('原始得分：',sim)

.5 归一化

为了将注意力得分转换为概率分布，需按行对得分矩阵进行 $softmax$ 操作，确保每行的和为 1，得到的矩阵表示每个元素对其他元素的注意力权重。是的，包括自己。
$$\text{Attention Weight}=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)$$

具体到每行的公式如下：
$${\hat{\alpha }}_{1,i}=\frac{\exp ({\alpha }_{1,i})}{{\sum }_j\exp ({\alpha }_{1,j})}$$

• ${\alpha }_{1,i}$ ：第 $1$ 个词语和第 $i$ 个词语之间的原始注意力得分。
• ${\hat{\alpha }}_{1,i}$ ：经过归一化后的注意力得分。

    score = F.softmax(sim, dim=-1)# print('归一化操作：', score)

2.6 加权求和

通过将注意力权重矩阵与值矩阵 $V$ 相乘，得到加权的值表示。
$$\text{Output}=\text{Attention Weight}\times V=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)\times V$$

   # 加权求和：我（一开始的词向量）不再是我(通过上下文进行加权求和之后的我)output = torch.matmul(score, V)print( output[0])

具体计算示意图如下：

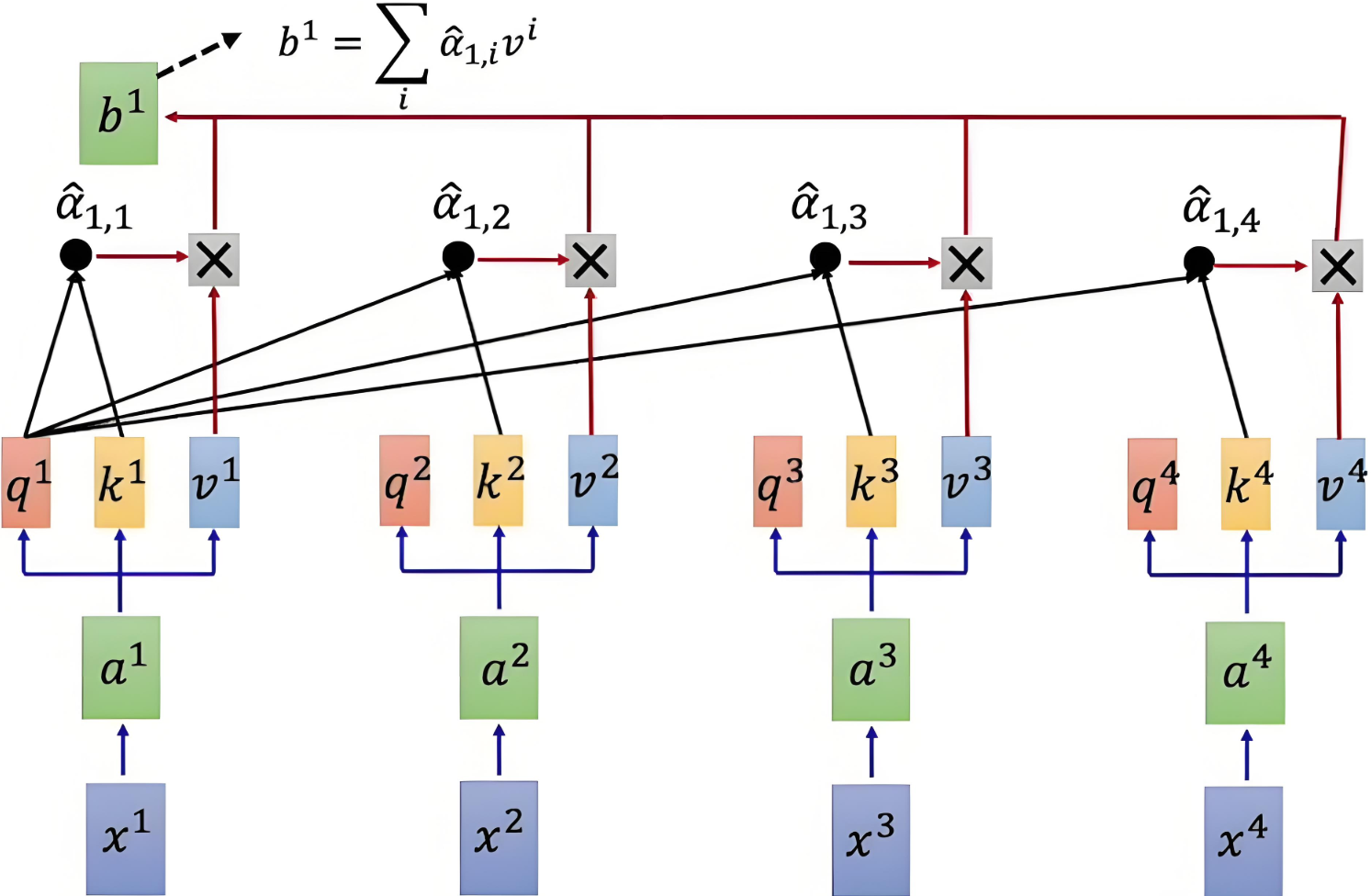
| Q和K计算相似度后，经 $softmax$ 得到注意力，再乘V，最后相加得到包含注意力的输出 |

3. 多头注意力机制

Multi-Head Attention，多头注意力机制，是对自注意力机制的扩展。

3.1 基本概念

多头注意力机制的核心思想是，将注意力机制中的 $Q、K、V$ 分成多个头，每个头计算出独立的注意力结果，然后将所有头的输出拼接起来，最后通过一个线性变换得到最终的输出。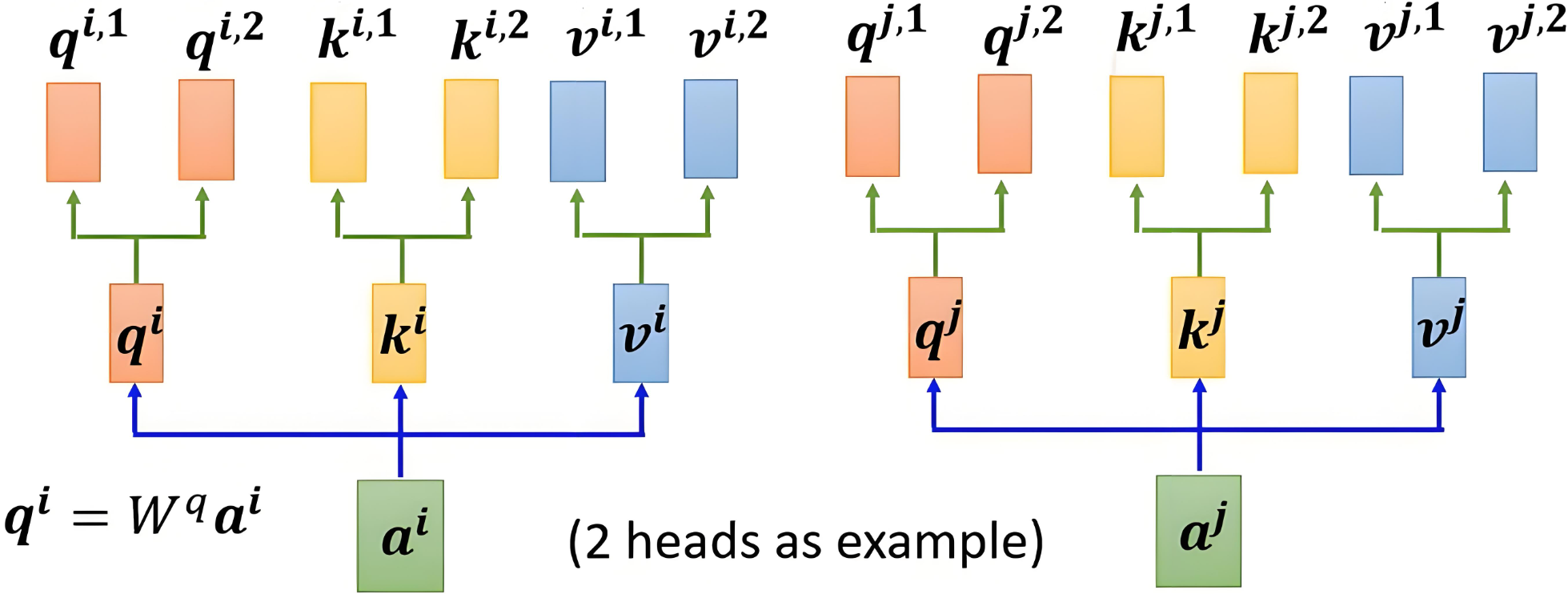
3.2 多头机制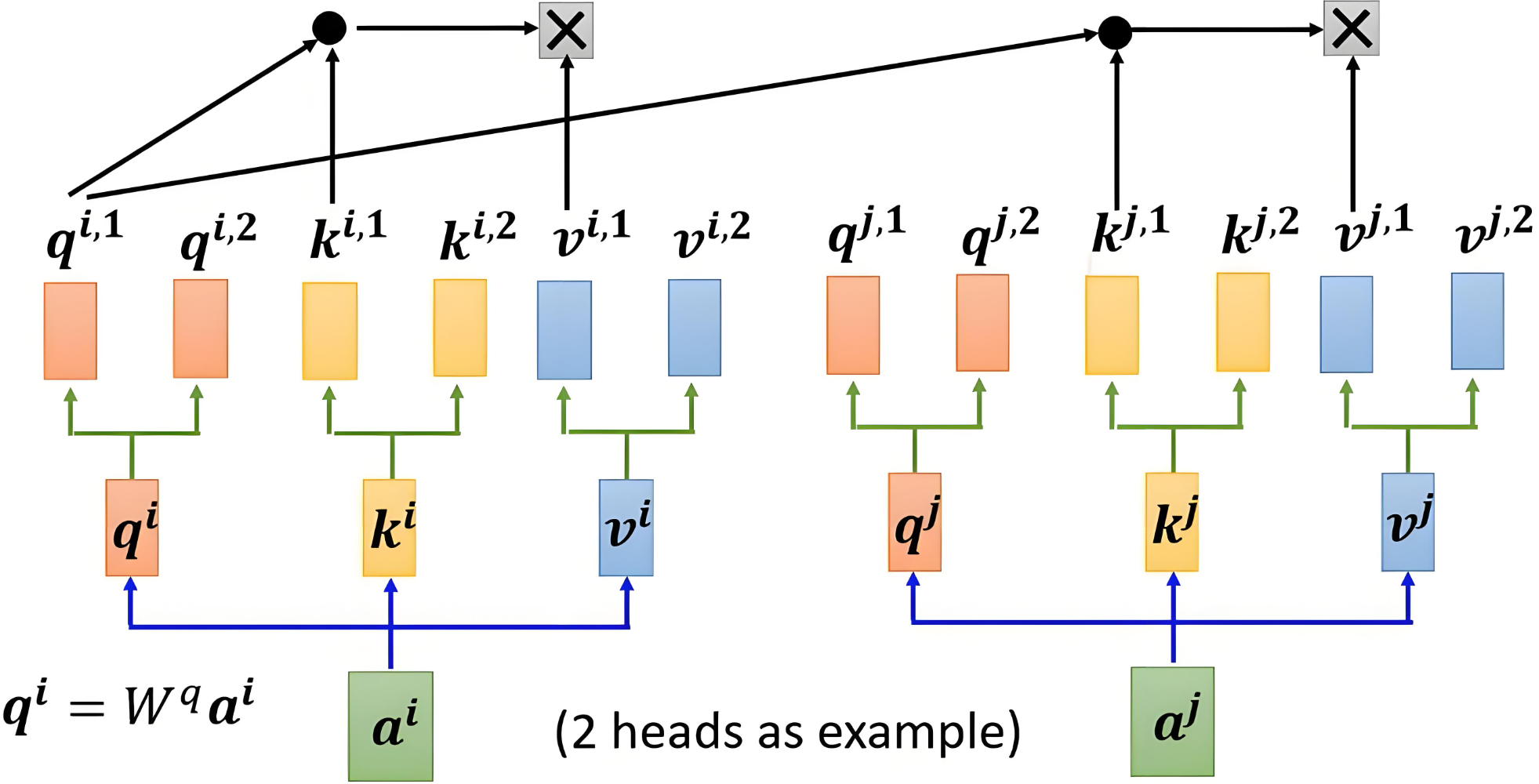

3.2.1 映射权重

分头的过程是通过权重矩阵映射实现的，而不是直接切分

 head_num=8head_dim=dim // head_numfc=nn.ModuleList(nn.Linear(dim,dim) for _ in range(3))#映射QueryKeyValue矩阵Q=fc[0](sentence_embedding)K=fc[1](sentence_embedding)V=fc[2](sentence_embedding)#分成八个头#每个映射创建出八个线性层multi_head_Q_fc=nn.ModuleList(nn.Linear(dim, head_dim) for _ in range(head_num))multi_head_K_fc=nn.ModuleList(nn.Linear(dim, head_dim) for _ in range(head_num))multi_head_V_fc=nn.ModuleList(nn.Linear(dim, head_dim) for _ in range(head_num))#将不同的注意力头进行映射然后堆叠起来multi_head_Q = torch.stack([multi_head_Q_fc[i](Q) for i in range(head_num)])print(multi_head_Q.shape)multi_head_K = torch.stack([multi_head_K_fc[i](K) for i in range(head_num)])print(multi_head_K.shape)multi_head_V = torch.stack([multi_head_V_fc[i](V) for i in range(head_num)])print(multi_head_V.shape)

3.3 加权求和

每个头是独立计算的，使用自己的一套参数，得到每个头的输出：
$$O_h=A_h{V}_h$$
其中，$O_h\in {\mathbb{R}}^{n\times d_v}$ 是第 $h$ 个头的输出。

  # 计算各自的注意力得分scores_list = torch.stack([torch.matmul(Query_list[i], Key_list[i].transpose(0, 1))for i in range(head_num)])scores_list = torch.stack([scores_list[i] / math.sqrt(d_k) for i in range(head_num)])# 进行归一化操作scores_list = torch.stack([F.softmax(scores_list[i], dim=-1) for i in range(head_num)])print(scores_list)

3.4 输出拼接

将所有头的输出进行拼接：
$$O_{\text{concat}}=[O_1,O_2,\dots ,O_h]\in {\mathbb{R}}^{n\times h\cdot d_v}$$
其中，$O_{\text{concat}}$ 是所有头拼接的结果，维度是 $n\times (h\cdot d_v)$，其中 $h$ 是头的数量，$d_v$ 是每个头的值向量的维度。

# 对8个头进行拼接，拼接形状：(seq_len, d_k)Output = torch.cat(Output_list, dim=-1)print(Output.shape) # torch.Size([7, 512])

3.5 线性变换

拼接后通过一个线性变换矩阵 $W^O$ 映射为最终输出：
$$\text{Output}=O_{\text{concat}}{W}^O$$
其中，$W^O\in {\mathbb{R}}^{(h\cdot d_v)\times d}$ 是可训练的权重矩阵，$d$ 是最终输出的维度。

  # 线性变换并最终输出W_O = torch.randn(dim, dim)Output = torch.matmul(Output, W_O)print(Output.shape) # torch.Size([7, 512])

3.3 表达能力

通过多个并行的头在不同的子空间中学习上下文信息，让同一个句子在不同场景下表达不同的意思，增强模型的表达能力和灵活性。