Blender模拟结构光3D Scanner(一)外参数匹配
如何使用Blender模拟FPP(Fringe Projection Profilometry) 原理的结构光3D传感器?
主要包含的工作有:
1)相机、投影仪定位与内外参数匹配;
2)投影仪投射指定Pattern图像;
3)被测物体材质属性配置等;
本篇主要关注外参数匹配。
外参数匹配的基本思路 是,添加Camera和SpotLight节点,并设置各自的变换(Transform)属性,主要是位置和旋转
六个参数。
1 Blender中变换参数的含义
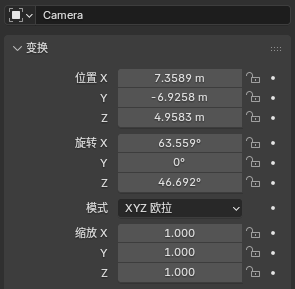
Blender中,变换参数的含义可理解为世界坐标系到当前Object坐标系的变换,用位置和旋转
可分别表示为
和
。
则Object坐标系下的点与该点在世界坐标系下的坐标
之间的变换关系为
(1-1)
2 左相机变换参数配置
在三维测量中惯用的相机坐标系定义为,
—— 相机画幅平面内水平向右的方向为
正方向;
—— 相机画幅平面内竖直向下的方向为
正方向;
—— 相机观测正前方(Front)方向为
正方向;
但Blender中,相机坐标系的定义是不同的。具体表现为,在Blender中将相机变换参数的位置和旋转
都设置为0,如图1所示。
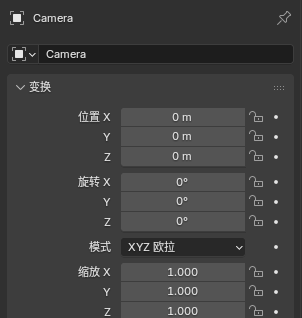
图1 相机位置和旋转参数置0
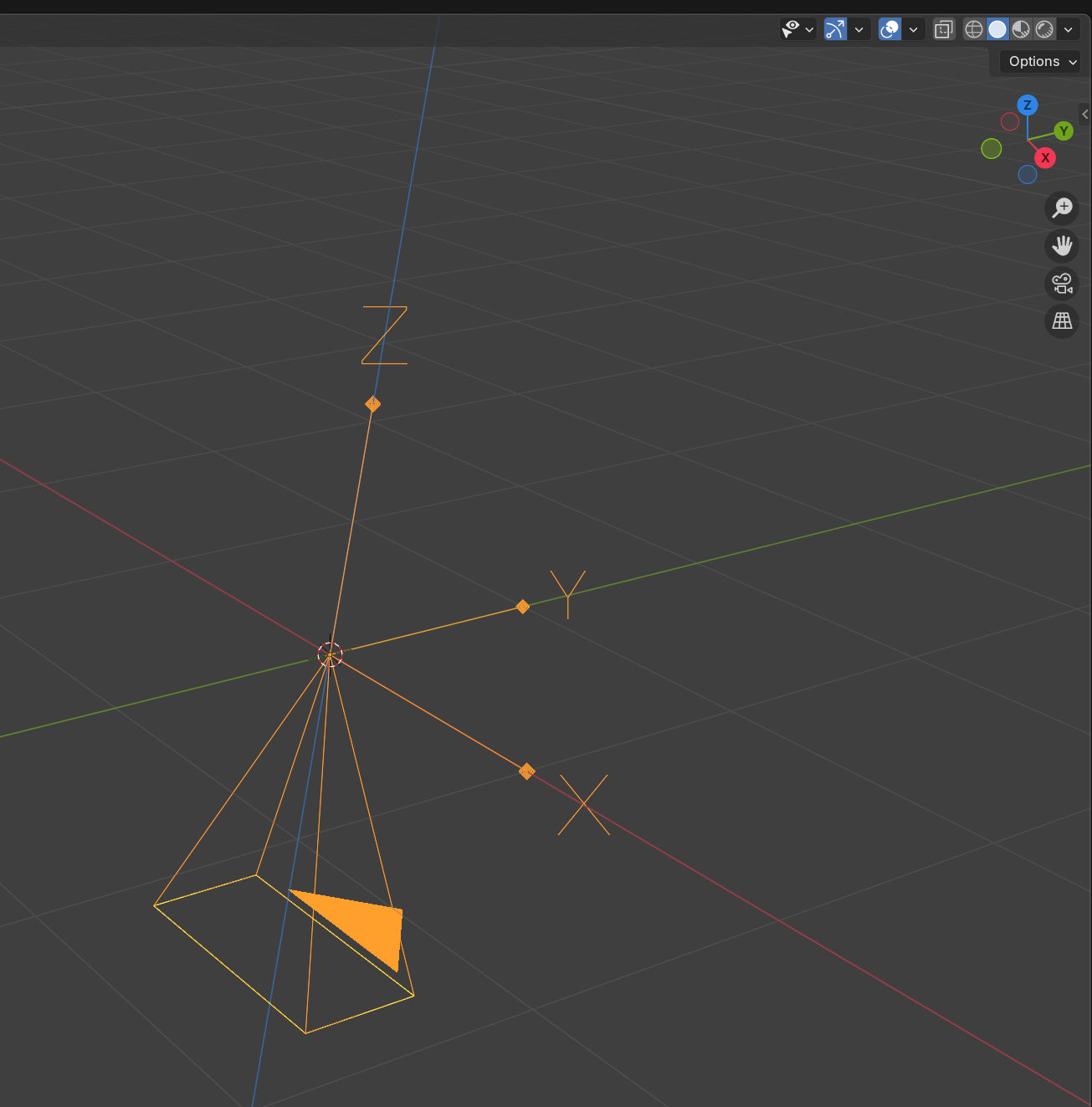
图2 相机视野和方向
此时相机的视野和方向如图2,图中和红色/绿色/蓝色线为世界坐标系三轴的轴线, 三个轴的正方向可参见右上角的坐标轴缩略图(彩色实心圆指向轴的正方向);图中橙色线段,端点标有
的是相机坐标系;相机的视野前方为世界坐标系的
负方向,相机视野的上方向为世界坐标系的
正方向。
为了使相机的视野前方与上方向与三维测量中惯用的相机相匹配,需要设置Blender中相机旋转变换参数,旋转轴均设置180°,如图3所示。设置后,相机视野前方指向
正方向,视野上方指向
负方向。
但注意此时Blender中相机坐标系(橙色)的各轴方向为:
—— 与世界坐标系
正方向一致;
—— 与世界坐标系
正方向相反;
—— 与世界坐标系
正方向相反;
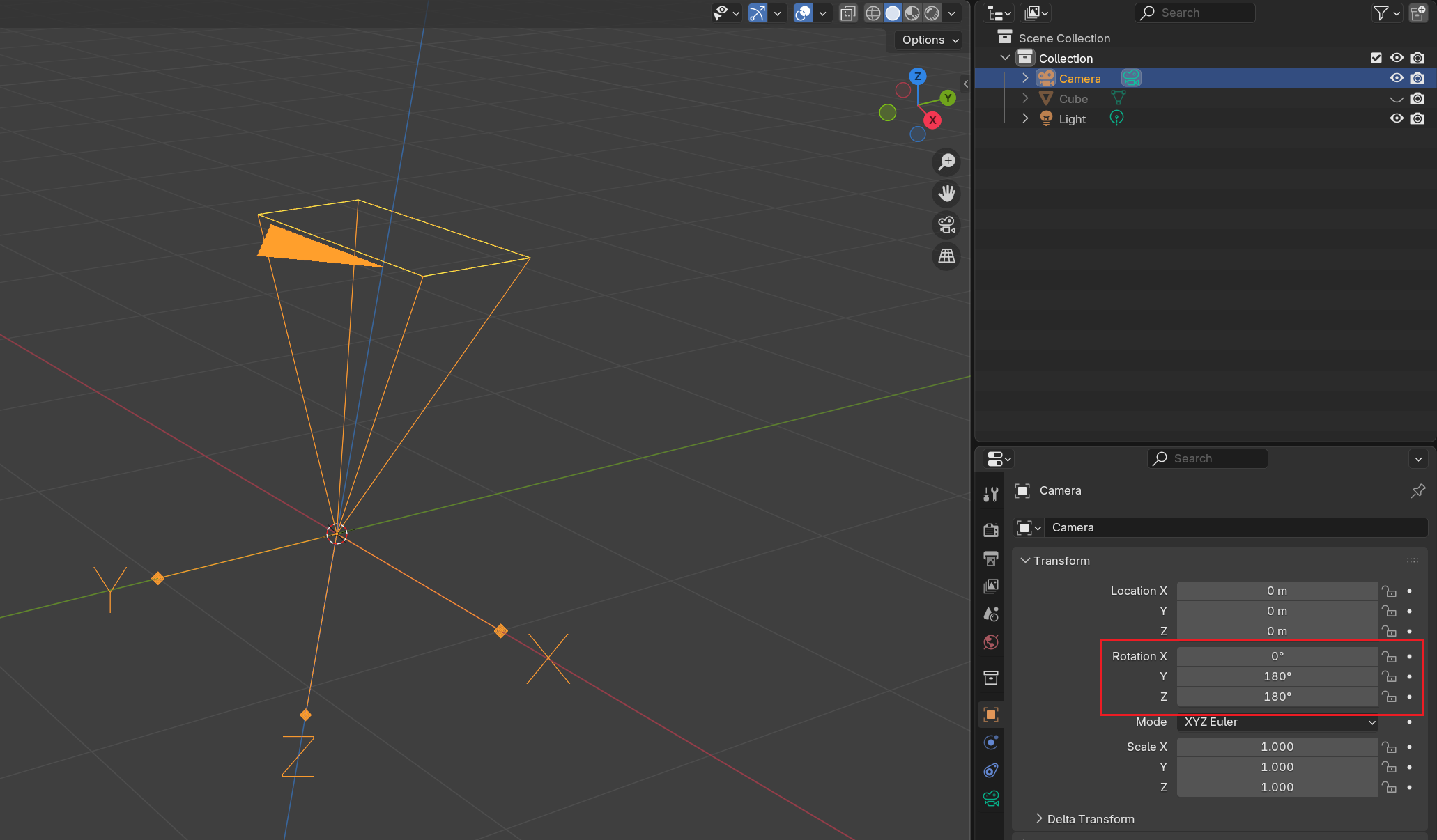
图3 旋转轴均设置180°后的Blender相机坐标系
根据式(1-1),此时Blender相机坐标系下点的坐标与该点在世界坐标系下的表示
的关系为
(2-1)
式中,对应旋转变换参数
轴均设置180°。
但是,此时Blender相机坐标系和三维测量惯用的相机坐标系(本节开头)定义仍是不同的,若在此时Blender相机节点的位置,建立三维测量惯用的相机坐标系,设该坐标系下点的坐标为,则
与该点在Blender相机坐标系下的坐标
之间的变换关系为
(2-2)
式中,对应旋转变换参数
轴旋转180°,即Blender相机坐标系绕
轴旋转180°可构造出三维测量惯用的相机坐标系。
3 投影仪变换参数配置
投影仪和双目系统中右相机的地位是相同的。在Blender中可通过设置聚光灯(Spot Light)+图像纹理的方式来模拟投影仪的效果。参考式(1-1),配置投影仪变换参数即确定与
(3-1)
聚光灯的坐标系(即投影仪坐标系)与第2节中Blender相机坐标系的定义是类似的,也存在Blender投影仪坐标系与三维测量惯用的投影仪坐标系差距旋转的问题,即
(3-2)
若三维测量系统标定外参数已知,即三维测量惯用的投影仪坐标系与三维测量惯用的左相机坐标系的变换关系已知,则有
(3-3)
联立式(2-1)、(2-2)、(3-1)、(3-2)、(3-3)可求得投影仪变换旋转参数和平移参数
,即可对应得到Blender聚光灯的变换参数。
(3-4)
(3-5)
注意,式中可理解为分别绕
三个轴各转了180°,相当于没有转!
所以有
(3-6)
最终实验得到的一组投影仪变换参数和相机-投影仪位置关系如图4所示
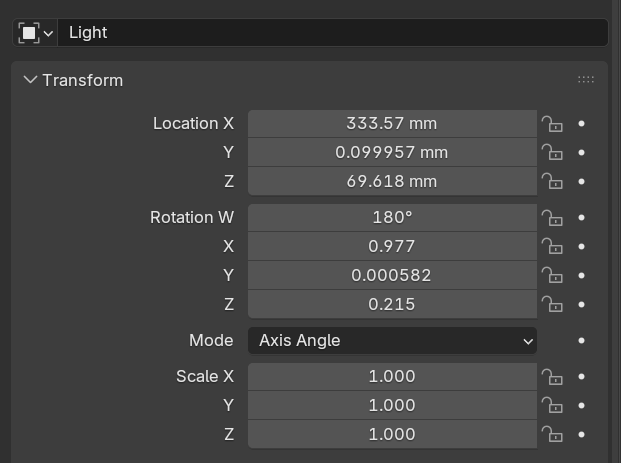
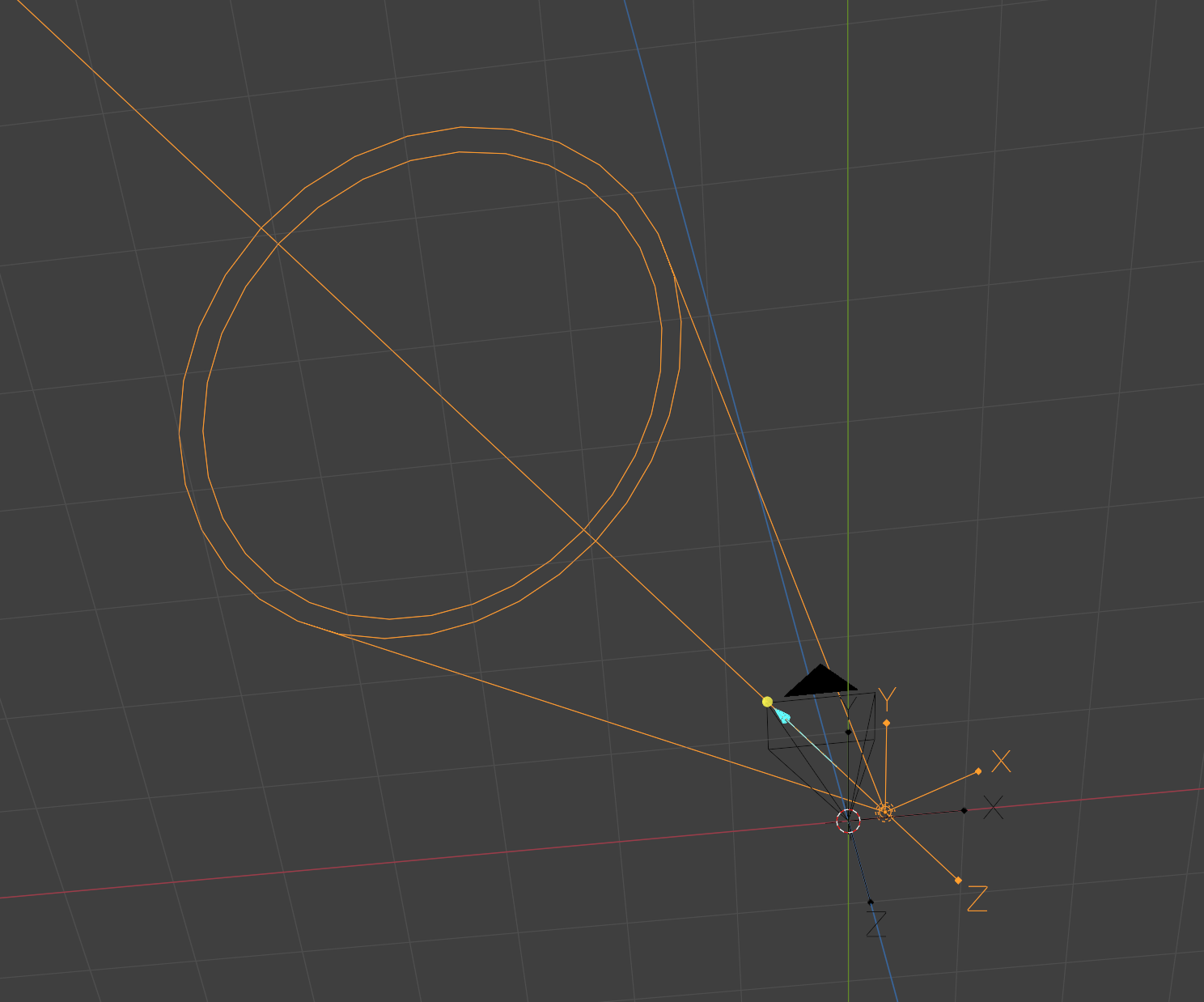
图4 实验得到的一组投影仪变换参数和相机-投影仪位置关系
