当前位置：首页 > news >正文

栈和队列：数据结构中的基础与应用

news 2025/8/13 12:49:50

栈和队列：数据结构中的基础与应用

请添加图片描述

在计算机科学的领域中，数据结构犹如大厦的基石，支撑着各类复杂软件系统的构建。而栈和队列作为两种基础且重要的数据结构，以其独特的特性和广泛的应用，在程序设计的舞台上扮演着不可或缺的角色。

栈：“后进先出” 的存储容器

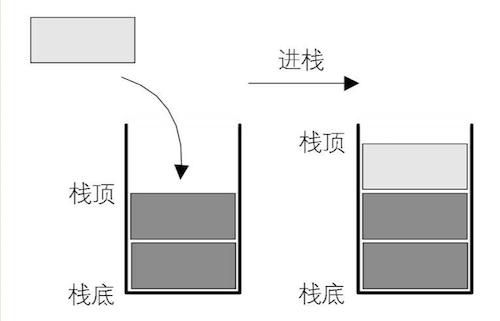
栈是一种特殊的线性表，其特殊性体现在操作的局限性上。它只允许在固定的一端进行数据的插入和删除操作，这一端被称为栈顶，另一端则是栈底。这种操作限制使得栈呈现出 “先进后出”（LIFO，Last In First Out）的逻辑特性。在日常生活中，栈的身影随处可见。比如堆叠的盘子，我们总是先取用最后放上去的盘子；函数调用时，最后调用的函数会最先返回；在文档编辑软件中，撤销操作也是按照最近的修改最先被撤销的顺序进行。

从实现方式来看，栈主要有顺序栈和链式栈两种。顺序栈基于顺序表实现，利用连续的内存空间来存储元素，并通过管理结构体记录栈的状态，如栈的总容量、栈顶下标等。链式栈则借助单链表实现，每个链表节点存储一个元素，同样有管理结构体来维护栈顶指针、当前元素个数以及栈容量限制等信息。

以顺序栈的操作为例，初始化栈时，需要为存储元素的数组分配内存空间，并将栈顶下标初始化为 -1，表示空栈。入栈操作时，首先判断栈是否已满，若未满，则将栈顶下标加 1，然后在对应的数组位置存储新元素。出栈操作则先检查栈是否为空，若不为空，先获取栈顶元素，再将栈顶下标减 1 。相关代码实现如下：

// 顺序栈结构体
typedef struct node {DATA *stack; // 存储元素的数组首地址int size; // 栈的总容量int top; // 栈顶下标(初始为-1表示空栈)
}SeqStack;// 初始化栈
int sstack_init(SeqStack *s, int num) {s->data = (DATA *)calloc(num, sizeof(DATA));if(s->data == NULL) return -1;s->size = num;s->top = -1; return 0;
}// 数据入栈/压栈
int sstack_push(SeqStack *s, DATA data) {if(sstack_isfull(s)) return -1;s->top++; s->data[s->top] = data; return 0;
}// 数据出栈/弹栈
int sstack_pop(SeqStack *s, DATA *data) {if(sstack_isempty(s)) return -1;*data = s->data[s->top];s->top--;return 0;
}

栈的优点显著，操作简单高效，由于仅对栈顶进行操作，其时间复杂度为 O (1) 。并且，“后进先出” 的特性使其在处理对称性、嵌套性问题时得心应手。例如在表达式求值（中缀转后缀）和括号匹配检查中，栈能够有效地解决这些问题。然而，栈也存在一定的局限性，它只能直接访问栈顶元素，顺序栈还存在容量限制，而链式栈则有额外的指针开销。

栈在实际应用中十分广泛。在函数调用过程中，系统会利用栈来保存函数调用的相关信息，如返回地址、局部变量等，确保函数能够正确地返回和执行。在浏览器的前进后退功能中，同样运用了栈的原理，用户访问过的页面地址被依次压入栈中，通过对栈的操作实现前进和后退的功能。

队列：“先进先出” 的有序序列

队列同样是一种特殊的线性表，它的特殊之处在于只能在固定的两端进行操作，一端用于插入元素，称为队尾；另一端用于删除元素，称为队头。这种操作方式使得队列呈现出 “先进先出”（FIFO，First In First Out）的特性，与现实生活中的排队现象极为相似。例如在银行排队办理业务，先来的客户先接受服务；打印队列中，先提交的文档先被打印；消息队列里，先到达的消息先被处理。

队列的存储实现主要有循环队列和链式队列。循环队列基于数组实现，通过巧妙的模运算实现了数组空间的循环利用。为了区分队空和队满的状态，通常会牺牲一个存储单元。链式队列则借助链表节点存储元素，通过维护队头指针和队尾指针来管理队列。

以循环队列的操作为例，初始化循环队列时，需要为存储数组分配内存空间，并将队头下标和队尾下标都初始化为 0 。入队操作时，先判断队列是否已满，若未满，则在队尾下标对应的数组位置存储新元素，然后更新队尾下标。出队操作则先检查队列是否为空，若不为空，先获取队头元素，再更新队头下标。相关代码实现如下：

// 循环队列结构体
typedef struct {DATA *data; // 存储数组int size; // 队列容量int front; // 队头下标(出队维护队头下标)int rear; // 队尾下标(入队维护队尾下标)
}SQueue;// 初始化循环队列
int squeue_init(SQueue *q, int size) {q->data = (DATA *)calloc(size, sizeof(DATA));if (q->data == NULL)return -1;q->size = size;q->front = q->rear = 0;return 0;
}// 元素入队
int squeue_enqueue(SQueue *q, DATA data) {if (squeue_isfull(q))return -1;q->data[q->rear] = data;q->rear = (q->rear + 1) % q->size; return 0;
}// 元素出队
int squeue_dequeue(SQueue *q, DATA *data) {if (squeue_isempty(q))return -1;*data = q->data[q->front];q->front = (q->front + 1) % q->size;return 0;
}

队列的优点在于 “先进先出” 的特性保证了操作的公平性，并且支持高效的队头和队尾操作。循环队列在访问速度上具有优势，适合固定大小场景；链式队列则能动态扩容，适用于大小不确定的场景。但队列也有其缺点，它只能直接访问队头和队尾元素，循环队列还存在固定容量限制。

队列在众多领域有着广泛的应用。在任务调度中，如打印队列，能够按照任务提交的先后顺序依次执行任务。在消息队列中，确保消息按照到达的先后顺序被处理，避免消息混乱。在广度优先搜索（BFS）算法中，队列用于存储待访问的节点，保证了搜索的广度优先特性。在缓冲池管理和多线程编程中的生产者 - 消费者模式中，队列也发挥着重要作用，实现了数据的有序传递和共享。

乱。在广度优先搜索（BFS）算法中，队列用于存储待访问的节点，保证了搜索的广度优先特性。在缓冲池管理和多线程编程中的生产者 - 消费者模式中，队列也发挥着重要作用，实现了数据的有序传递和共享。

栈和队列作为基础的数据结构，虽然看似简单，却蕴含着强大的功能和广泛的应用价值。它们为解决各种复杂的编程问题提供了有效的工具和思路，无论是在系统软件的底层实现，还是在应用软件的功能开发中，都占据着举足轻重的地位。深入理解和熟练运用栈和队列，将为我们在计算机科学的道路上奠定坚实的基础。

查看全文

http://www.dtcms.com/a/328412.html