当前位置：首页 > news >正文

机器学习-集成学习（EnsembleLearning）

news 2025/8/13 12:41:27

0 结果展示

0.1 鸢尾花分类

import pandas as pd
import numpy as npfrom sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, f1_score, classification_report, roc_auc_score,confusion_matrix
from sklearn.datasets import load_iris
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifierimport matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题iris = load_iris()
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data["target"] = iris.target
X = data.drop(columns="target")
y = data["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)rf = RandomForestClassifier(n_estimators=100,criterion="gini",  # 分裂的标准max_depth=None,  # 不限制深度min_samples_leaf=1,min_samples_split=2,)
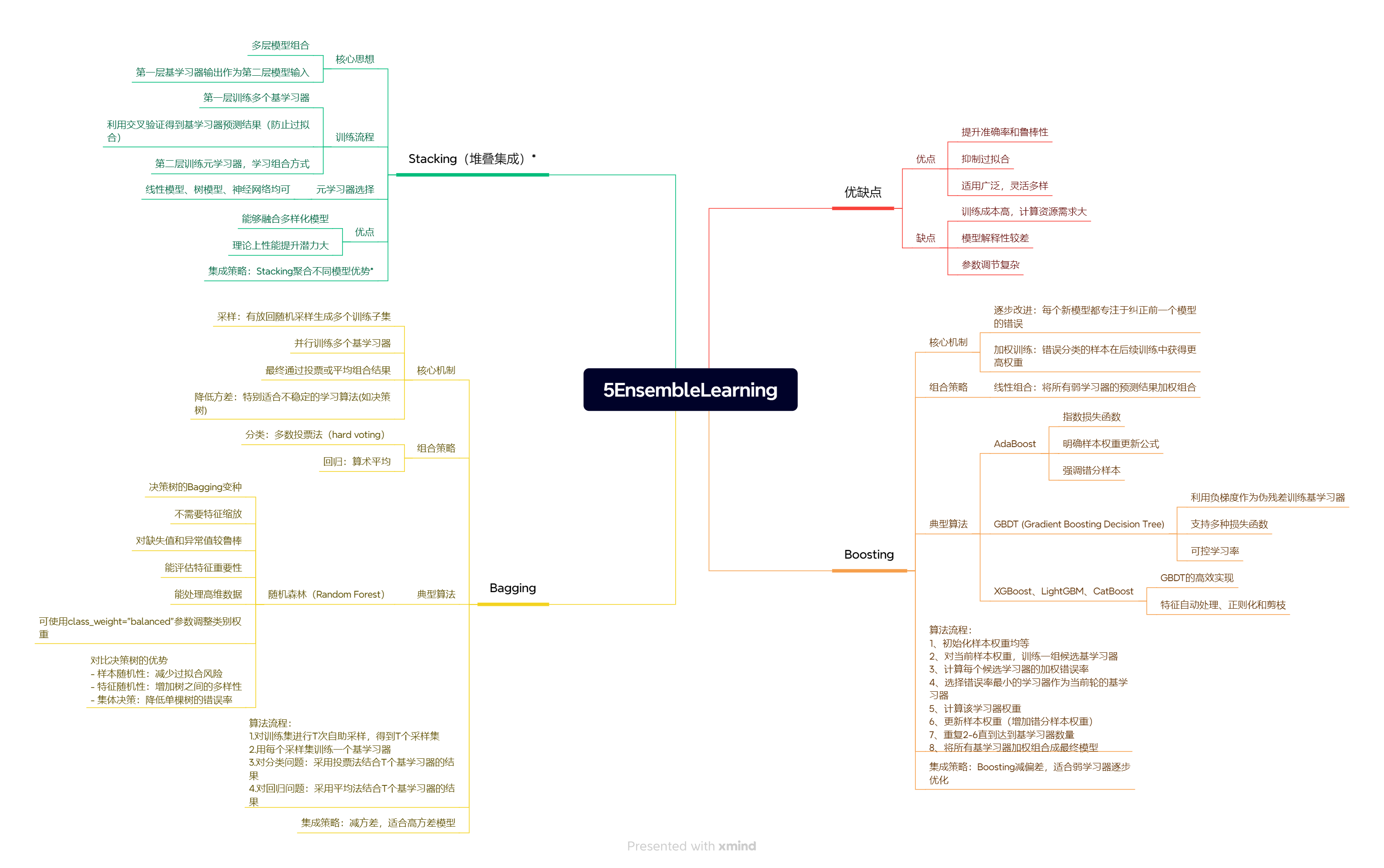
rf.fit(X_train, y_train)y_pred = rf.predict(X_test)df = pd.DataFrame({"feature": X.columns,"importance": rf.feature_importances_
})
print("classification_report：")
print(classification_report(y_test, y_pred))
print("confusion_matrix:")
print(confusion_matrix(y_test, y_pred))
df.sort_values(by="importance", inplace=True, ascending=False)  # 降序
plt.figure(figsize=(10,8))
plt.bar(df.feature, df.importance,color = ["b","g","r","pink"])
plt.show()

在这里插入图片描述

0.2 信用卡欺诈检测

data = pd.read_csv("../data/creditcard.csv")
import pandas as pd
import numpy as npfrom sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, f1_score, classification_report, roc_auc_score,confusion_matrix
from sklearn.datasets import load_iris
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
# 数据集划分
X=data.drop(columns=["Time","Class"])
y=data["Class"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,stratify=y.values,random_state=42)
# 特征工程
#标准化
transfer = StandardScaler()
X["Amount"] = transfer.fit_transform(X["Amount"].to_frame())# fit_transform只接受二维
# 训练
rf = RandomForestClassifier(n_estimators=100,class_weight="balanced",n_jobs=-1,
)  # class_weight根据类别的比例采样，因为1和0类别数量差距太大了
rf.fit(X_train, y_train)
#验证
y_pred = rf.predict(X_test)
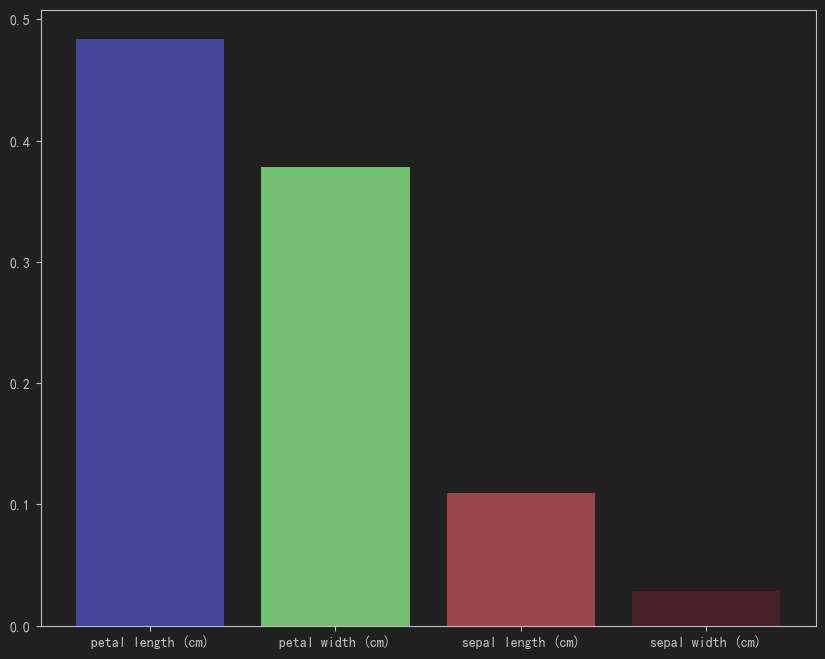
y_pred_proba = rf.predict_proba(X_test)print(classification_report(y_test, y_pred))
fpr,tpr,_ = roc_curve(y_test,y_pred_proba[:,1]) # 计算fpr和tpr,这个函数只需要正类，所以不用指定label,只需呀指定pos_label
# 绘制ROC 曲线
plt.figure(figsize=(10,5))
plt.plot(fpr,tpr,color="blue",label="ROC")
plt.plot([0,1],[0,1],color="red",linestyle="--")
#
plt.title("ROC")
plt.plot(fpr,tpr,label='ROC')
plt.plot([0,1],[0,1],linestyle='--')
plt.show()
AUC =roc_auc_score(y_test,y_pred_proba[:,1])
print(AUC)

(集成中的算法大多数情况都是用树模型去做的，几乎没有其他模型去做)

1 Bagging

1】什么是Bagging

Bagging(Bootstrap Aggregating)是一种并行式集成学习方法
核心思想是通过对训练样本进行有放回的随机抽样(自助采样法)，构建多个弱学习器，然后对这些学习器的预测结果进行投票或平均。

2】Bagging的关键特点

‌自助采样(Bootstrap Sampling)‌：从原始训练集中有放回地随机抽取n个样本(n通常等于原始训练集大小)
‌并行训练‌：基学习器之间相互独立，可以并行训练
‌降低方差‌：特别适合不稳定的学习算法(如决策树)
‌简单投票/平均‌：分类问题用投票，回归问题用平均

3】Bagging算法流程

1.对训练集进行T次自助采样，得到T个采样集
2.用每个采样集训练一个基学习器
3.对分类问题：采用投票法结合T个基学习器的结果
4.对回归问题：采用平均法结合T个基学习器的结果

1.1 随机森林

sklearn.ensemble.RandomForestClassifier(n_estimators=10,
criterion=’gini’,
max_depth=None,
bootstrap=True,
random_state=None,
min_samples_split=2
)

参数：
1】n_estimators：integer，optional(default = 10)森林⾥的树⽊数量120,200,300,500,800,1200
在利⽤最⼤投票数或平均值来预测之前，你想要建⽴⼦树的数量。
2】Criterion：string，可选(default =“gini”)
分割特征的测量⽅法
3】max_depth：integer或None，可选(默认=⽆)
树的最⼤深度 5,8,15,25,30
4】max_features=“auto”,每个决策树的最⼤特征数量
If “auto”, then max_features=sqrt(n_features)
If “sqrt”, then max_features=sqrt(n_features) (same as “auto”).
If “log2”, then max_features=log2(n_features)
If None, then max_features=n_features
5】bootstrap：boolean，optional(default = True)
是否在构建树时使⽤放回抽样
6】min_samples_split 内部节点再划分所需最⼩样本数
这个值限制了⼦树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择
最优特征来进⾏划分，默认是2。
如果样本量不⼤，不需要管这个值。
如果样本量数量级⾮常⼤，则推荐增⼤这个值。
7】min_samples_leaf 叶⼦节点的最⼩样本数
这个值限制了叶⼦节点最少的样本数，如果某叶⼦节点数⽬⼩于样本数，则会和兄弟节点⼀起被剪枝，
默认是1。
叶是决策树的末端节点。较⼩的叶⼦使模型更容易捕捉训练数据中的噪声。
⼀般来说，我更偏向于将最⼩叶⼦节点数⽬设置为⼤于50。
8】min_impurity_split: 节点划分最⼩不纯度
这个值限制了决策树的增⻓，如果某节点的不纯度(基于基尼系数，均⽅差)⼩于这个阈值，则该节点不再⽣成⼦节点。即为叶⼦节点。
⼀般不推荐改动默认值1e-7。
9】class_weight：调整类别权重
balanced：自动按样本数的反比给出权重：n_samples / (n_classes * np.bincount(y))
balanced_subsample：与"balanced” 类似，但仅基于每次自助抽样后的子样本计算权重

1.2随机森林常见问题

1 为什么随机森林比单棵决策树好？

样本随机性：减少过拟合风险
特征随机性：增加树之间的多样性
集体决策：降低单棵树的错误率

2 如何选择n_estimators参数？

开始时选择较小的值(如50-100)
观察验证集性能随树数量增加的变化
当性能不再显著提升时停止增加
计算资源允许的情况下可以设置较大值

3 如何处理类别不平衡问题？

使用class_weight="balanced"参数调整类别权重
对少数类进行过采样
使用balanced_subsample参数(自助采样时保持类别比例)

4 随机森林有哪些优缺点？
‌优点‌：

高准确性
能处理高维数据
能评估特征重要性
对缺失值和异常值较鲁棒
不需要特征缩放

‌缺点‌：

模型解释性较差
训练时间可能较长(树多时)
可能占用较多内存

**常规bagging实现，以决策树为例 **

from sklearn.ensemble import RandomForestClassifier
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score,f1_score, classification_report,roc_auc_score
from sklearn.datasets import load_iris
from sklearn.ensemble import  BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data["target"] = iris.target
X=data.drop(columns="target")
y= data["target"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=42)
#%%
# bagging
bagging = BaggingClassifier(estimator=DecisionTreeClassifier(),  #  弱学习器设置为决策树n_estimators=100, # 100棵决策树max_samples=0.8, # 每次采样80%的样本max_features=0.8, # 每次采样80%的特征random_state=42 , )
bagging.fit(X_train, y_train)y_pred = bagging.predict(X_test)
print(accuracy_score(y_test, y_pred))

随机森林实现

# rf
rf = RandomForestClassifier(n_estimators=100,criterion="gini",# 分裂的标准max_depth=None,  # 不限制深度min_samples_leaf=1,min_samples_split=2,)
rf.fit(X_train,y_train)y_pred = rf.predict(X_test)
print(accuracy_score(y_test, y_pred))df = pd.DataFrame({"feature" : X.columns,"importance" : rf.feature_importances_
})
df.sort_values(by="importance",inplace=True,ascending=False)# 降序
df

2 可视化决策边界


import numpy as np
from sklearn.decomposition import PCA # 主成分降维
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
pca = PCA(n_components=2) # n_components表示需要降到几维，以便可视化
X_pca = pca.fit_transform(X)
train_X_pca, test_X_pca, train_y_pca, test_y_pca = train_test_split(X_pca,y,test_size=0.2,random_state=42)rf_pca = RandomForestClassifier(n_estimators=100,)
rf_pca.fit(train_X_pca,train_y_pca)# ---------------1 创建网格点 1----------------------------------
# 网格点的主要目的是为了可视化"测试点"
# 1.绘制决策边界
# 2.填充颜色区域
# 3.展示分类的效果X_min,X_max = X_pca[:,0].min()-1,X_pca[:,0].max()+1 # 根据第一个主要成分定义X轴范围。+1和-1防止样本正好在边界上
y_min,y_max = X_pca[:,1].min()-1,X_pca[:,1].max()+1 # 根据第二个主要成分定义Y轴范围。xx,yy = np.meshgrid(np.arange(X_min,X_max,0.02), # 根据范围创建等差数列作为一个个网格np.arange(y_min,y_max,0.02), # 根据范围创建等差数列作为一个个网格
)
#---------2 此时已经生成了一个空白的网格面板 2---------# 预测网格点，将xx，yy网格矩阵变成一维数组(x,y)
"注意np.c_后面跟的是中括号"
Z = rf_pca.predict(np.c_[xx.ravel(), yy.ravel()])  # ravel()将网格矩阵变为一维,
# np.c_[]  # 将两个一维数组按列合并成一个二维数组
# 格式： [[x1,y1],[x2,y2],[x3,y3]........]#---------3 以上操作用已经训练好的rf_pca对每一个网格点均进行预测，故当(xx[i],yy[i])的元素处于会被分类为0的坐标时就会被分类为0，其他类别也是， 3 -------------
# --------3 ，此时Z为0，1，2的三个类别，每个网格点都被划分好了类别 3-----------# 绘制决策边界
Z = Z.reshape(xx.shape)#-----------------4 将分类好的网格点重新reshape为原来的形状，否则无法画出来，为contourf绘制作准备 4-------------------------------
plt.figure(figsize=(10,8))#--------------------------5 绘制----------------------------------
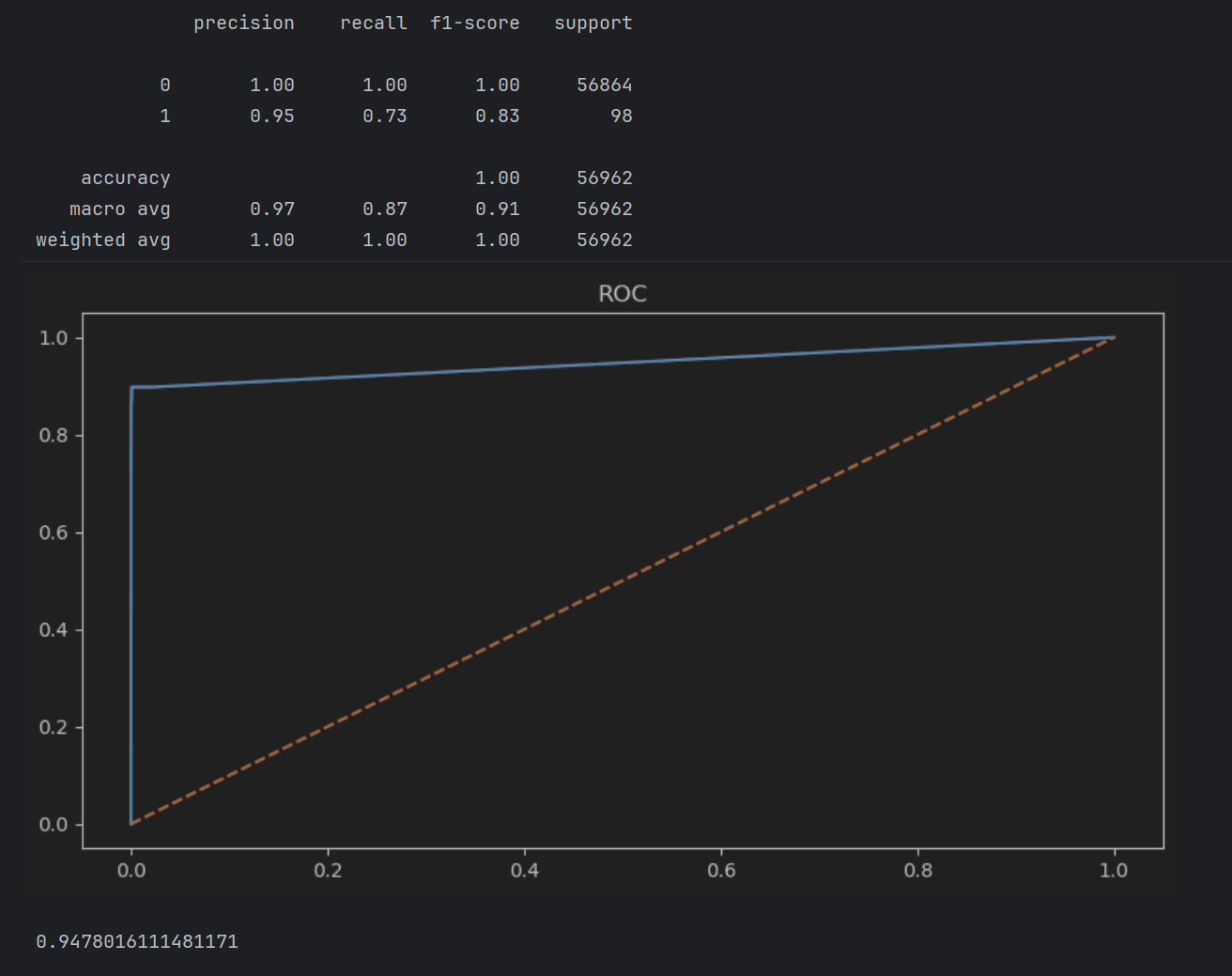
plt.contourf(xx, yy, Z, ) # xx和yy表示了每个网格点，Z表示了每个网格点的类型，故第三个参数需要和xx和yy形状相同
plt.scatter(X_pca[:,0], X_pca[:,1],c=y,edgecolors="k") # c=y表示用目标值进行着色，逐个着色，标签不同颜色不同
plt.title("随机森林决策边界的可视化")
plt.xlabel("主要成分1")
plt.ylabel("主要成分2")plt.show()

在这里插入图片描述

3 boosting

1】什么是Boosting
Boosting是一种序列式集成学习方法，通过将多个弱学习器（如决策树桩）组合成一个强学习器。
与Bagging不同，Boosting的基学习器是顺序训练的，每个基学习器都会尝试修正前一个学习器的错误。

2】Boosting的核心思想

‌逐步改进‌：每个新模型都专注于纠正前一个模型的错误
‌加权训练‌：错误分类的样本在后续训练中获得更高权重
‌线性组合‌：将所有弱学习器的预测结果加权组合

3】Boosting工作流程

1. 初始化样本权重均等
1. 对当前样本权重，训练学习器 $h_t$
1. 计算该学习器的加权错误率 $ϵ=∑i=1mwi(t)⋅I(h(xi)≠yi)\epsilon = \sum_{i=1}^m w_i^{(t)} \cdot I(h(x_i) \neq y_i)$ （ $h(x_i)$ 表示对样本i的预测， $I$ 表示如果括号内条件为真(即预测错误)则返回1，否则返回0）
1. 计算该学习器权重 $αt\alpha_t$ , $αt=12ln⁡1−ϵtϵt\alpha_t = \frac{1}{2} \ln \frac{1 - \epsilon_t}{\epsilon_t}$ .
1. 更新样本权重（注意非学习器权重）, $wi(t+1)=wi(t)⋅exp⁡(−αtyiht(xi))Ztw_i^{(t+1)} = \frac{w_i^{(t)} \cdot \exp(-\alpha_t y_i h_t(x_i))}{Z_t}$ (这一步是Ada的做法，梯度提升树是通过求残差的梯度来逼近最优权重)
1. 重复步骤2-6直到达到预设的基学习器数量
1. 将所有基学习器加权组合成最终模型

4】常见Boosting算法

1.AdaBoost (Adaptive Boosting)
2.Gradient Boosting
3.XGBoost
4.LightGBM
5.CatBoost

3.1 GradientBoostingClassifier和AdaBoostClassifier

3.1 api实现

api:
from sklearn.ensemble import AdaBoostClassifier,GradientBoostingClassifier

AdaBoost模型:
AdaBoostClassifier(
estimator=DecisionTreeClassifier(max_depth=1),
n_estimators,
learning_rate,
random_state=42
)

Gradient Boosting模型:
GradientBoostingClassifier(
n_estimators,
learning_rate,
max_depth,
random_state
)
plt.show()
#%% md

3.2 Boosting算法常见问题

1 如何选择n_estimators和learning_rate？

n_estimators‌：开始时选择中等大小(50-100)，观察验证误差随树数量增加的变化
learning_rate‌：通常选择较小的值(0.01-0.1)，较小的学习率通常需要更多的树

2 Boosting容易过拟合吗？

AdaBoost相对不容易过拟合
Gradient Boosting容易过拟合，可以通过以下方法控制：
减小max_depth
增加min_samples_leaf
使用早停(early stopping)
添加子采样(subsample)

3 为什么Gradient Boosting通常比AdaBoost表现更好？
Gradient Boosting直接优化损失函数，可以处理更多样的问题，并且对异常值不那么敏感。

4什么时候应该使用Boosting？

当需要高预测精度时
当数据质量较好(噪声和异常值较少)时
当有足够的计算资源时(特别是对于大型数据集)
#%% md

3.3 boosting算法对比

特性	AdaBoost	Gradient Boosting
核心思想	调整样本权重	梯度下降优化损失函数
基学习器	通常是决策树桩(max_depth=1)	通常是较浅的决策树
学习率	有	有(更关键)
对异常值敏感性	较敏感	较不敏感
训练速度	较快	较慢
过拟合风险	较低	较高
主要参数	n_estimators, learning_rate	n_estimators, learning_rate, max_depth

boosting实现

from sklearn.ensemble import RandomForestClassifier
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, f1_score, classification_report, roc_auc_score
from sklearn.datasets import load_iris
from sklearn.ensemble import BaggingClassifier,AdaBoostClassifier, GradientBoostingClassifier
from sklearn.tree import DecisionTreeClassifier
import numpy as np
from sklearn.decomposition import PCA  # 主成分降维
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题
# plt.rcParams['image.cmap'] = 'plasma'  # 设置默认调色板为 plasma
iris = load_iris()
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data["target"] = iris.target
X = data.drop(columns="target")
y = data["target"]pca.fit_transform(X)
train_X_pca ,test_X_pca,train_y_pca ,test_y_pca = train_test_split(X,y,test_size=0.2)
train_X_pca = pca.fit_transform(train_X_pca)
test_X_pca = pca.transform(test_X_pca)
# 训练
Ada = AdaBoostClassifier()
Ada.fit(train_X_pca,train_y_pca)
GB = GradientBoostingClassifier()
GB.fit(train_X_pca,train_y_pca)
# 创建网格范围
x_min ,x_max = train_X_pca[:,0].min()-1,train_X_pca[:,0].max()+1
y_min ,y_max =train_X_pca[:,1].min()-1,train_X_pca[:,1].max()+1
# 根据范围创建网格
xx,yy = np.meshgrid(np.arange(x_min,x_max,0.02),np.arange(y_min,y_max,0.02)
)
# 预测网格类别
Ada_Z = Ada.predict(np.c_[xx.ravel(),yy.ravel()])
Ada_Z = Ada_Z.reshape(xx.shape)
GB_Z = GB.predict(np.c_[xx.ravel(),yy.ravel()])
GB_Z = GB_Z.reshape(xx.shape)# 绘制
plt.figure(figsize=(10,8))
fig,axes = plt.subplots(1,2,figsize=(20,8))
axes[0].contourf(xx,yy,Ada_Z)
axes[0].scatter(train_X_pca[:,0],train_X_pca[:,1],c=train_y_pca,edgecolors="k")
axes[0].set_title("AdaBoostClassifier决策边界")
axes[0].set_xlabel("主成分1")
axes[0].set_ylabel("主成分2")
axes[1].contourf(xx,yy,GB_Z)
axes[1].scatter(train_X_pca[:,0],train_X_pca[:,1],c=train_y_pca,edgecolors="k")
axes[1].set_title("GradientBoostingClassifier决策边界")
axes[1].set_xlabel("主成分1")
axes[1].set_ylabel("主成分2")plt.show()

3.4 GradientBoostingClassifier算法介绍*

2 GBDT的核心思想

‌梯度提升‌：通过梯度下降来最小化损失函数
‌决策树基学习器‌：使用决策树作为弱学习器
‌残差学习‌：每个新树学习前序模型的残差
‌加法模型‌：将多个弱学习器的预测结果累加

3 GBDT工作流程

1】初始化模型（常数值预测）
2】对于每轮迭代（每棵树）：
- 计算当前模型的负梯度（伪残差）
- 用伪残差拟合一棵决策树
- 通过线搜索确定最优步长
- 更新模型（将新树的预测乘以学习率后加到原模型）
3】组合所有树的预测结果

4 GBDT的关键特点
1】优点

‌高预测精度‌：在多种任务上表现优异
‌特征组合‌：自动学习高阶特征组合
‌鲁棒性‌：对异常值和缺失值有一定鲁棒性
‌灵活性‌：可处理各种损失函数

2】缺点

‌训练时间较长‌：需要顺序构建多棵树
‌内存消耗大‌：需要存储多棵树
‌参数敏感‌：需要仔细调参

5 与随机森林的区别

特性	GBDT	随机森林
基学习器关系	顺序训练	并行训练
目标	减少偏差	减少方差
树相关性	高度相关	低相关
过拟合风险	较高	较低
参数敏感性	更敏感	较不敏感