传输线的效应
以前在学习电路学时,只知道一条金属导线,是一条完美短路的导线。直到修习微波工程之后才发现导线没那么单纯。
在高频微波的世界中,传输线的阻抗不像在直流电路一样,一条导线定义成短路这么简单。而是会随着频率在不同的导线传输距离下有不同的阻抗。讲白话来说,就是不同频率的电可以走的距离不一样。概念就像,想像自己是个灵魂,每穿过一面墙就要来回一次(正负极快速变化),而有一条无限面墙的隧道,而每穿过一次墙面,就会变透明一点直到消失。所以你是高频率穿梭的灵魂,穿过墙面的次数就高,你在这条隧道走的距离就越短。应该还算好理解吧XD,既然高频的传输线不能用电路学的单一导线来解释,那要如何解释呢?
这就要翻开微波工程的书籍,在第二章节的传输线理论,传输线经常用双导线来表示[1]。可以看到在两导线上不在像电路学中那么单纯(图a),只是电压与电流。而是电压的函数V(z, t)与电流的函数I(z, t),而传输线的长度有△Z的变化量,表示阻抗Z是会随着距离的不同又所变化。但传输线也可以用电路学的元件观念来解释,如图b。但定义不太一样,主要多了每单位长度的元件值R, L, G, C。
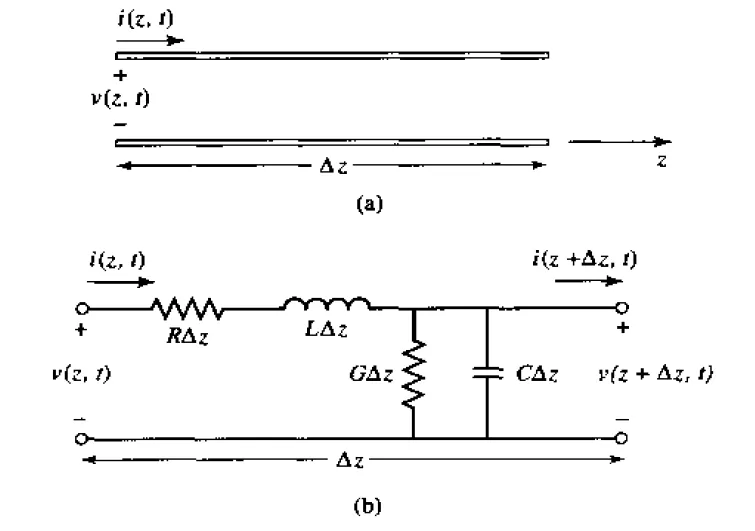
传输线模型(a)电压与电流的定义(b)集总元件的等效电路[1]
R→两导体单位长度的串联电阻Ω/m
L→两导体单位长度的串联电感H/m
R→两导体单位长度的并联电导S/m
R→两导体单位长度的并联电容F/m
其物理意义可解释成两导体的自感L、上下导体电极形成电容C、导体本身的电阻R、两导体间的介电损耗G。后面就可以用到基本电学所教的柯西赫夫电压与电流定律推导出电压与电流是会随着频率有关系。
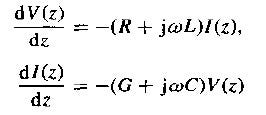
而将这个联立方程式整理一下会得出二阶的微分方程式,并可以推导出传输线上的电压函数:
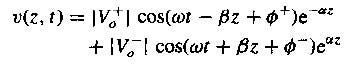
可以分成V+与V-两个余弦的形式。有兴趣可以参考微波工程。然而推出这个式子其实只要说明传输线是有两个电位V+与V-组成,而电压的大小会随着相位变化,影响相位的参数有频率与波速(相速,波),其中的α为导线的衰减量(上面提到灵魂穿过墙面的能量损失),电流亦同此概念。而波速就是阻抗的斜率(阻抗的变化速度),讲白话就是波能量由低到高(高到低)的速度。

而k(β)称为相位常数或波数,物理意义就是波在介质中走2π的距离所产生的波,在传输线就是每公尺的传输线有几个波(β)。
我个人觉得要设计传输线或了解传输线特性,一定要了解下列图表的参数与公式。

当然我今天不是要告诉大家怎么设计传输线,而是一个概念。其中要特别提到当我们在说波长时介质都是空气(真空),所以公式λ=c/f,波速都是以光速在做计算,但事实上传输线的介质并非空气,而是一些铁氟龙金属材料,故速度会比光速来得低一点,可以在上面的公式看出来跟波数有关,而波数又跟介电常数有关。
有了传输线的概念后,会想既然传输线都不传输了(阻抗变化非定值),那怎么要怎么将不同的高频讯号传输呢?答案在特征阻抗,一般通同轴电缆线的特征阻抗为50欧姆,这也是我们常将阻抗匹配至50欧姆的原因,他是一个统一定义值。而定义为L与C之间的比值开根号,其中的L与C为传输线上的分布元件(并非实体的元件),特征阻抗Z0并非实数的电阻,在理想上的传输线不消耗任何能量。微带线作为传输线时,Z0的值取决于PCB材料,基底厚度,线宽等。所以特征阻抗是可以被设计的,像我们看电视在使用的传输线为75欧姆,而非50欧姆。
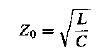
以下图来解释传输线阻抗的定义,从PORT (Z)看进去的阻抗会是有传输线的特征阻抗加上ZL。可以整理出下列公式。
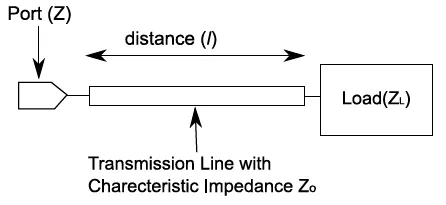
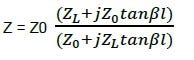
将到这里一定会纳闷有这个公式有什么用?答案就在tan里!高中有学过三角函数就知道,Tan函数在90度时为正负无限大。
也就是说,传输线长度l=λ/4时,ZL=0而Z=∞,ZL=∞而Z=0,就是如果传输线是传输频率的四分之一波长,开路变短路,短路变开路。而ZL=Z0(50欧姆),特性为在任意点的传输线阻抗皆相同。
换个角度想,只要小于四分之一波长的传输线,其实都保有电感、电容特性,我们可以由开路与短路的结构来等校电感电容,由传输线长度(小于λ/4)来决定电性大小,这里的波长是要用电讯号在传输线的波速来计算。
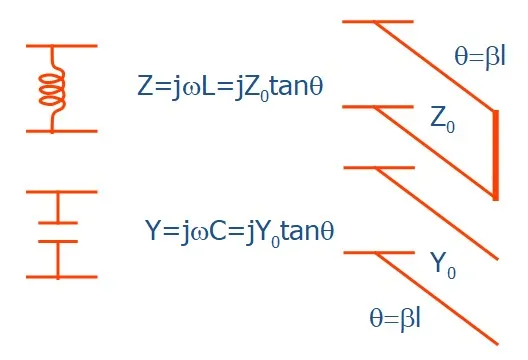
传输线结构short 和open stubs分别可以表示成集总元件电感与电容。基本上这些都算是传输线的皮毛而已,但这对于RF的layout设计或是天线设计占有很大的基础,各人觉得学会一些传输线的观念,对于天线的解读有很大的帮助。
参考资料
1. Microwave Engineering, David M. Pozar.
