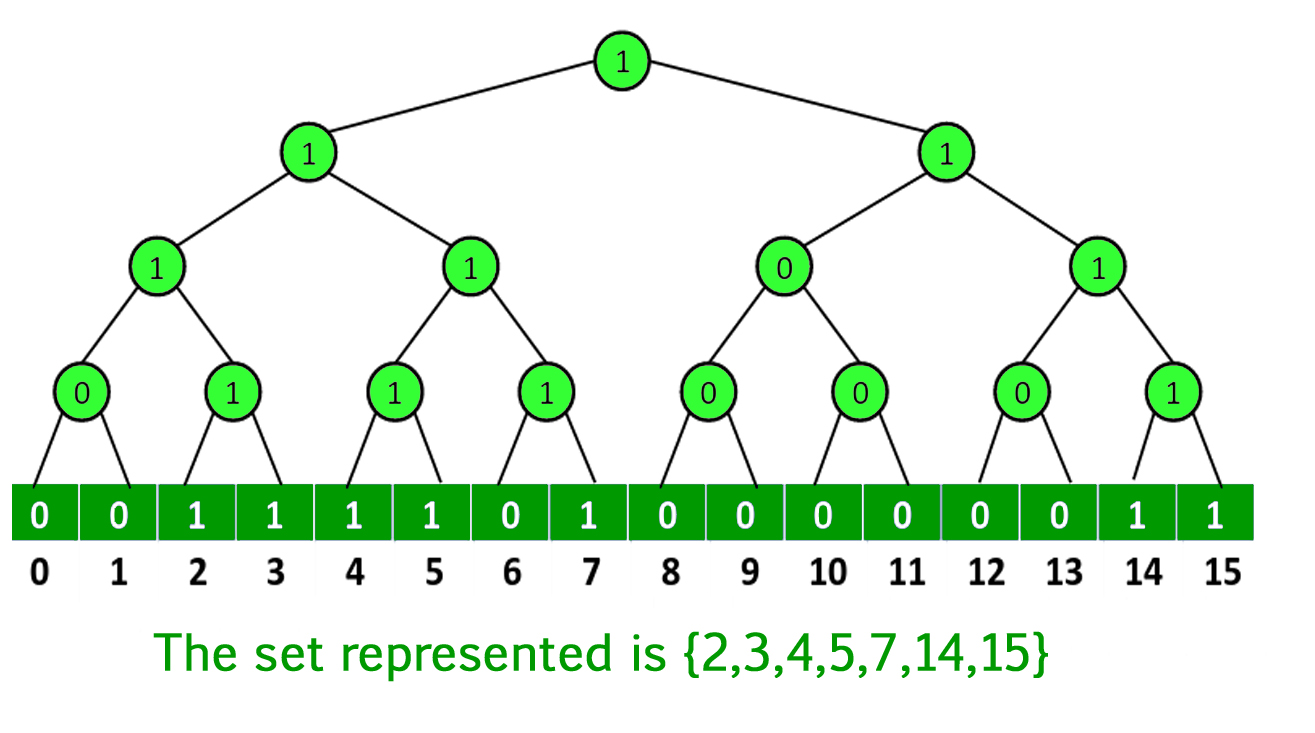
《算法导论》第 20 章 - van Emde Boas 树
引言
van Emde Boas 树(简称 vEB 树)是一种用于维护动态集合的高级数据结构,支持高效的插入、删除、查找、前驱和后继操作。与普通二叉搜索树的 O (log n) 时间复杂度不同,vEB 树能够在 O (log log n) 时间内完成这些操作,特别适用于需要处理大量整数键的场景。
本文将详细讲解 vEB 树的原理、实现和应用,帮助读者深入理解这一高效数据结构。
20.1 基本方法
vEB 树的核心思想是通过递归地将问题分解为更小的子问题,从而实现超对数时间复杂度的操作。它主要针对整数键的集合,假设所有键都在一个有限的范围内(0 到 u-1,其中 u 是 2 的幂)。
与其他数据结构相比,vEB 树的优势在于:
- 支持多种操作在 O (log log u) 时间内完成
- 特别适合处理大范围整数键的场景
- 递归结构设计巧妙,展现了分治思想的高级应用
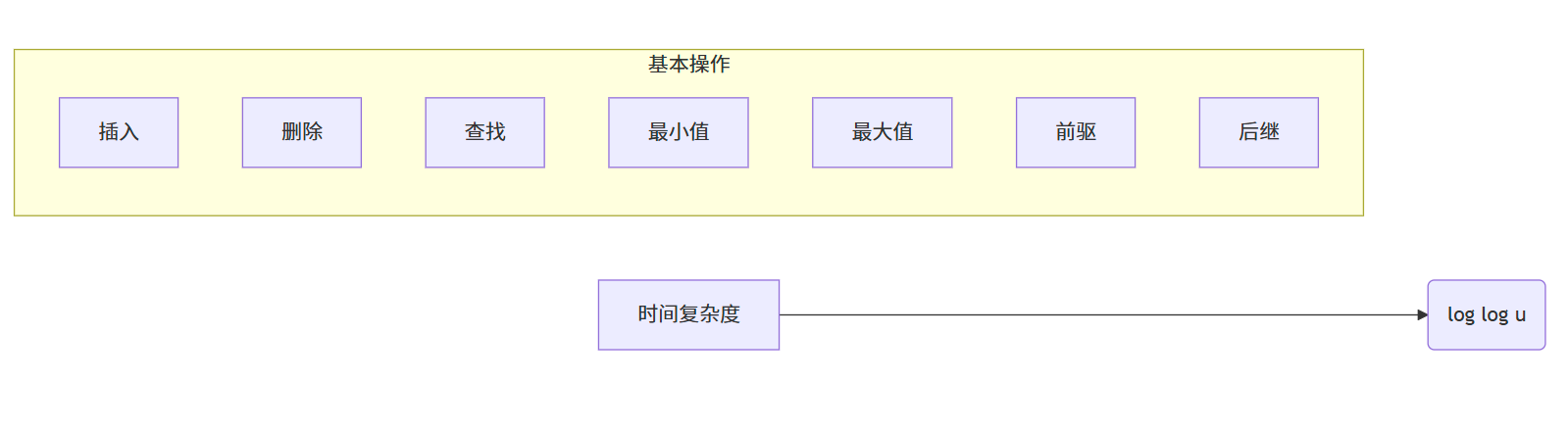
vEB 树的基本操作包括:
- 插入(insert):向集合中添加一个元素
- 删除(delete):从集合中移除一个元素
- 查找(member):判断一个元素是否在集合中
- 最小值(minimum):返回集合中的最小元素
- 最大值(maximum):返回集合中的最大元素
- 前驱(predecessor):返回小于给定元素的最大元素
- 后继(successor):返回大于给定元素的最小元素
20.2 递归结构
vEB 树采用递归的层次结构,将一个大范围的问题分解为多个小范围的子问题。这种递归分解是实现高效操作的关键。
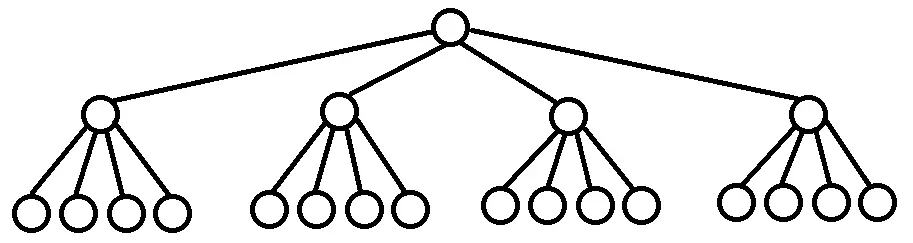
对于一个范围为 u 的 vEB 树,我们定义:

这种分解方式允许我们递归地构建 vEB 树结构。
20.2.1 原型 van Emde Boas 结构
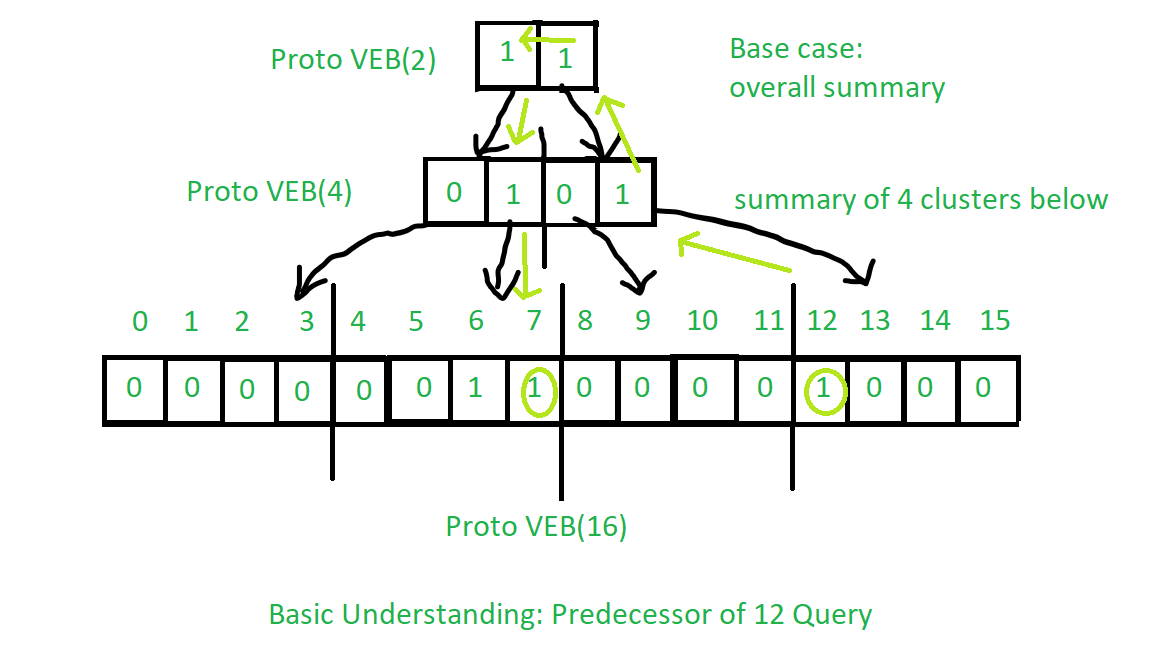
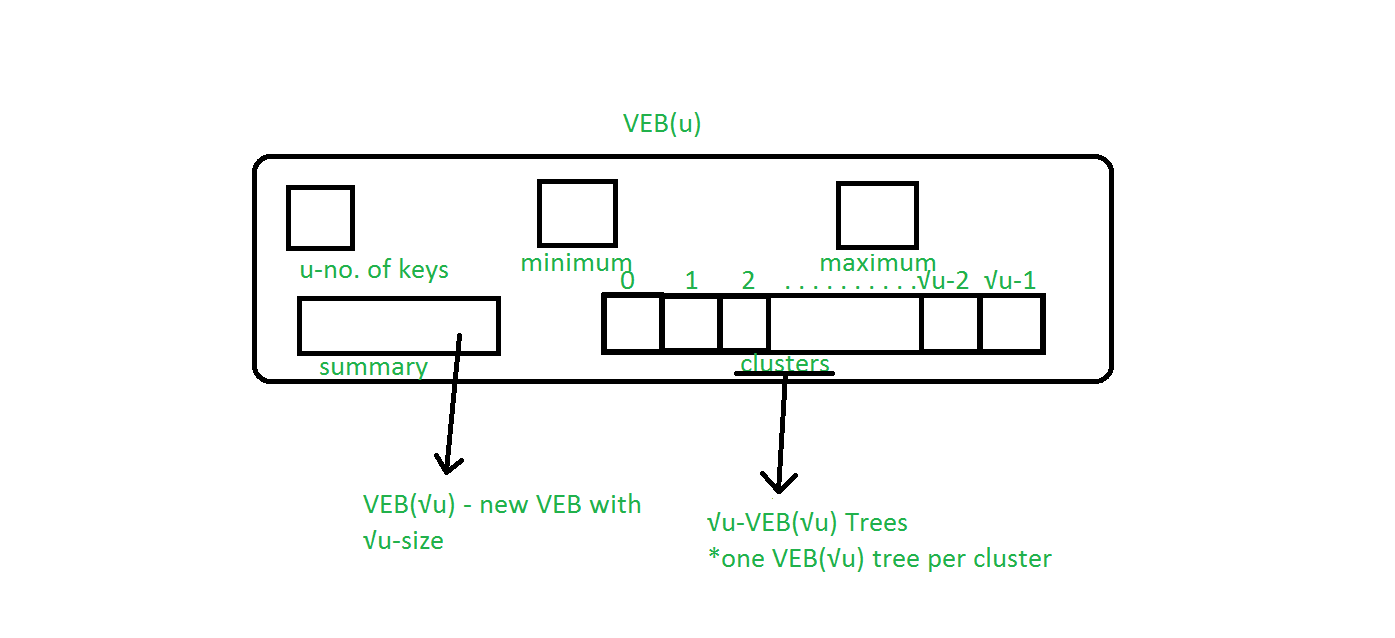
原型 vEB 结构(proto-vEB)是 vEB 树的基础,它包含以下几个部分:

@startuml
class ProtoVEB {- int u- int min- int max- ProtoVEB[] cluster- ProtoVEB summary+ ProtoVEB(int size)+ bool isMember(int x)+ int minimum()+ int maximum()+ void insert(int x)+ void delete(int x)+ int successor(int x)+ int predecessor(int x)
}
@enduml

原型 vEB 结构的递归定义如下:

20.2.2 原型 van Emde Boas 结构上的操作
下面我们实现原型 vEB 结构及其基本操作:
#include <iostream>
#include <vector>
#include <cmath>
#include <climits>// 原型van Emde Boas结构
class ProtoVEB {
private:int u; // 范围大小,u = 2^kint min; // 集合中的最小值int max; // 集合中的最大值std::vector<ProtoVEB*> cluster; // 簇数组ProtoVEB* summary; // 摘要结构// 计算sqrt(u),即2^(k/2)int sqrtu() const {return static_cast<int>(std::pow(2, std::log2(u) / 2));}// 计算high(x) = x / sqrt(u)int high(int x) const {return x / sqrtu();}// 计算low(x) = x % sqrt(u)int low(int x) const {return x % sqrtu();}// 计算index(high, low) = high * sqrt(u) + lowint index(int h, int l) const {return h * sqrtu() + l;}public:// 构造函数,初始化大小为size的proto-vEB结构ProtoVEB(int size) : u(size), min(INT_MAX), max(INT_MIN), summary(nullptr) {// 当u > 2时,需要初始化cluster和summaryif (u > 2) {int su = sqrtu();cluster.resize(su, nullptr);for (int i = 0; i < su; ++i) {cluster[i] = new ProtoVEB(su);}summary = new ProtoVEB(su);}}// 析构函数,释放内存~ProtoVEB() {if (u > 2) {for (auto c : cluster) {delete c;}delete summary;}}// 判断x是否在集合中bool isMember(int x) {// 边界检查if (x < 0 || x >= u) {return false;}// 基础情况:u=2if (u == 2) {return (x == min) || (x == max);}// 如果x是min或max,直接返回trueif (x == min || x == max) {return true;}// 否则递归检查相应的簇return cluster[high(x)]->isMember(low(x));}// 返回集合中的最小值int minimum() {return min;}// 返回集合中的最大值int maximum() {return max;}// 插入元素xvoid insert(int x) {// 边界检查if (x < 0 || x >= u) {return;}// 如果集合为空,直接设置min和maxif (min == INT_MAX) {min = x;max = x;return;}// 如果x小于当前最小值,交换x和minif (x < min) {std::swap(x, min);}// 如果u > 2且x不是最大值if (u > 2 && x != max) {int h = high(x);int l = low(x);// 如果簇为空,需要更新摘要if (cluster[h]->minimum() == INT_MAX) {summary->insert(h);}// 递归插入到相应的簇中cluster[h]->insert(l);}// 如果x大于当前最大值,更新maxif (x > max) {max = x;}}// 删除元素xvoid remove(int x) {// 边界检查if (x < 0 || x >= u || !isMember(x)) {return;}// 如果集合中只有一个元素if (min == max) {min = INT_MAX;max = INT_MIN;return;}// 基础情况:u=2if (u == 2) {min = (x == 0) ? 1 : 0;max = min;return;}// 如果x是最小值,需要找到新的最小值if (x == min) {// 找到第一个非空簇int first_cluster = summary->minimum();// 更新min为该簇中的最小值x = index(first_cluster, cluster[first_cluster]->minimum());min = x;}// 递归删除相应簇中的元素int h = high(x);int l = low(x);cluster[h]->remove(l);// 如果簇变为空,更新摘要if (cluster[h]->minimum() == INT_MAX) {summary->remove(h);}// 如果x是最大值if (x == max) {// 检查摘要是否为空if (summary->minimum() == INT_MAX) {// 集合中只剩下minmax = min;} else {// 找到最后一个非空簇,更新maxint last_cluster = summary->maximum();max = index(last_cluster, cluster[last_cluster]->maximum());}}}// 查找x的后继元素int successor(int x) {// 边界检查if (x < 0 || x >= u) {return INT_MAX;}// 基础情况:u=2if (u == 2) {// 如果x是0且1在集合中,返回1,否则返回INT_MAXif (x == 0 && max == 1) {return 1;} else {return INT_MAX;}}// 如果x小于min,返回minif (min != INT_MAX && x < min) {return min;}// 查找x所在簇中的最大值int h = high(x);int l = low(x);int max_low = cluster[h]->maximum();// 如果簇中存在大于x的元素,在该簇中查找后继if (max_low != INT_MIN && l < max_low) {int succ_low = cluster[h]->successor(l);return index(h, succ_low);} else {// 否则在其他簇中查找后继int succ_cluster = summary->successor(h);if (succ_cluster == INT_MAX) {return INT_MAX;} else {int succ_low = cluster[succ_cluster]->minimum();return index(succ_cluster, succ_low);}}}// 查找x的前驱元素int predecessor(int x) {// 边界检查if (x < 0 || x >= u) {return INT_MIN;}// 基础情况:u=2if (u == 2) {// 如果x是1且0在集合中,返回0,否则返回INT_MINif (x == 1 && min == 0) {return 0;} else {return INT_MIN;}}// 如果x大于max,返回maxif (max != INT_MIN && x > max) {return max;}// 查找x所在簇中的最小值int h = high(x);int l = low(x);int min_low = cluster[h]->minimum();// 如果簇中存在小于x的元素,在该簇中查找前驱if (min_low != INT_MAX && l > min_low) {int pred_low = cluster[h]->predecessor(l);return index(h, pred_low);} else {// 否则在其他簇中查找前驱int pred_cluster = summary->predecessor(h);if (pred_cluster == INT_MIN) {// 如果存在比所有簇中元素都小的min,返回minif (min != INT_MAX && x > min) {return min;} else {return INT_MIN;}} else {int pred_low = cluster[pred_cluster]->maximum();return index(pred_cluster, pred_low);}}}// 打印结构中的所有元素(用于测试)void printElements() {if (min == INT_MAX) {return;}std::cout << min << " ";if (u == 2) {if (max != min) {std::cout << max << " ";}return;}// 递归打印每个簇中的元素for (int i = 0; i < sqrtu(); ++i) {if (summary->isMember(i)) {// 保存当前min和max,避免递归打印时重复int curr_min = min;int curr_max = max;// 临时修改min和max,避免重复打印if (min == index(i, cluster[i]->minimum())) {min = INT_MAX;}if (max == index(i, cluster[i]->maximum())) {max = INT_MIN;}// 递归打印簇中的元素cluster[i]->printHelper(i);// 恢复min和maxmin = curr_min;max = curr_max;}}}private:// 辅助函数,用于打印簇中的元素void printHelper(int clusterIndex) {if (min == INT_MAX) {return;}std::cout << index(clusterIndex, min) << " ";if (u == 2) {if (max != min) {std::cout << index(clusterIndex, max) << " ";}return;}// 递归打印子簇中的元素for (int i = 0; i < sqrtu(); ++i) {if (summary->isMember(i)) {// 保存当前min和max,避免递归打印时重复int curr_min = min;int curr_max = max;// 临时修改min和max,避免重复打印if (min == index(i, cluster[i]->minimum())) {min = INT_MAX;}if (max == index(i, cluster[i]->maximum())) {max = INT_MIN;}// 递归打印子簇中的元素cluster[i]->printHelper(index(clusterIndex, i));// 恢复min和maxmin = curr_min;max = curr_max;}}}
};// 测试原型vEB结构
int main() {// 创建一个范围为16(2^4)的原型vEB结构ProtoVEB protoVEB(16);// 插入一些元素protoVEB.insert(2);protoVEB.insert(5);protoVEB.insert(8);protoVEB.insert(10);protoVEB.insert(14);std::cout << "插入元素后,集合中的元素为:";protoVEB.printElements();std::cout << std::endl;std::cout << "最小值: " << protoVEB.minimum() << std::endl;std::cout << "最大值: " << protoVEB.maximum() << std::endl;int x = 6;std::cout << "元素 " << x << " 的后继是: " << protoVEB.successor(x) << std::endl;std::cout << "元素 " << x << " 的前驱是: " << protoVEB.predecessor(x) << std::endl;x = 5;std::cout << "删除元素 " << x << std::endl;protoVEB.remove(x);std::cout << "删除后,集合中的元素为:";protoVEB.printElements();std::cout << std::endl;x = 8;std::cout << "元素 " << x << " 是否在集合中? " << (protoVEB.isMember(x) ? "是" : "否") << std::endl;x = 5;std::cout << "元素 " << x << " 是否在集合中? " << (protoVEB.isMember(x) ? "是" : "否") << std::endl;return 0;
}
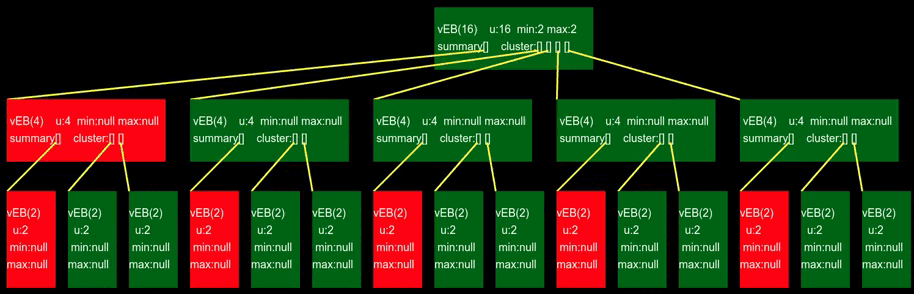
20.3 van Emde Boas 树及其操作
原型 vEB 结构虽然展示了基本思想,但在实际应用中效率不够高,因为它在递归过程中需要多次计算 sqrt (u)。van Emde Boas 树(简称 vEB 树)对原型结构进行了改进,通过预计算和存储一些关键值来提高效率。
20.3.1 van Emde Boas 树
vEB 树与原型 vEB 结构的主要区别在于:

vEB 树的结构定义如下:
@startuml
class VEBTree {- int u- int logu- int sqrtu- int min- int max- VEBTree[] cluster- VEBTree* summary+ VEBTree(int size)+ bool isMember(int x)+ int minimum()+ int maximum()+ void insert(int x)+ void delete(int x)+ int successor(int x)+ int predecessor(int x)+ void print()
}
@enduml

20.3.2 van Emde Boas 树的操作
下面是完整的 vEB 树实现代码,包含了所有基本操作:
#include <iostream>
#include <vector>
#include <cmath>
#include <climits>// van Emde Boas树实现
class VEBTree {
private:int u; // 范围大小,u = 2^loguint logu; // log2(u)int sqrtu; // sqrt(u) = 2^(logu/2)int min; // 集合中的最小值int max; // 集合中的最大值std::vector<VEBTree*> cluster; // 簇数组VEBTree* summary; // 摘要结构// 计算high(x) = floor(x / sqrtu)int high(int x) const {return static_cast<int>(floor(x / sqrtu));}// 计算low(x) = x % sqrtuint low(int x) const {return x % sqrtu;}// 计算index(high, low) = high * sqrtu + lowint index(int h, int l) const {return h * sqrtu + l;}public:// 构造函数,初始化大小为size的vEB树// 注意:size必须是2的幂VEBTree(int size) : u(size), min(INT_MAX), max(INT_MIN), summary(nullptr) {// 计算logu和sqrtulogu = static_cast<int>(log2(u));sqrtu = static_cast<int>(sqrt(u));// 当u > 2时,需要初始化cluster和summaryif (u > 2) {cluster.resize(sqrtu, nullptr);for (int i = 0; i < sqrtu; ++i) {cluster[i] = new VEBTree(sqrtu);}summary = new VEBTree(sqrtu);}}// 析构函数,释放内存~VEBTree() {if (u > 2) {for (auto c : cluster) {delete c;}delete summary;}}// 判断x是否在集合中bool isMember(int x) {// 边界检查if (x < 0 || x >= u) {return false;}// 如果x是min或max,直接返回trueif (x == min || x == max) {return true;}// 基础情况:u=2if (u == 2) {return false;}// 否则递归检查相应的簇return cluster[high(x)]->isMember(low(x));}// 返回集合中的最小值int minimum() const {return min;}// 返回集合中的最大值int maximum() const {return max;}// 插入元素xvoid insert(int x) {// 边界检查if (x < 0 || x >= u) {return;}// 如果集合为空,直接设置min和maxif (min == INT_MAX) {min = x;max = x;return;}// 如果x小于当前最小值,交换x和minif (x < min) {std::swap(x, min);}// 如果u > 2且x不是最大值if (u > 2 && x != max) {int h = high(x);int l = low(x);// 如果簇为空,需要更新摘要if (cluster[h]->minimum() == INT_MAX) {summary->insert(h);}// 递归插入到相应的簇中cluster[h]->insert(l);}// 如果x大于当前最大值,更新maxif (x > max) {max = x;}}// 删除元素xvoid remove(int x) {// 边界检查if (x < 0 || x >= u || !isMember(x)) {return;}// 如果集合中只有一个元素if (min == max) {min = INT_MAX;max = INT_MIN;return;}// 基础情况:u=2if (u == 2) {min = (x == 0) ? 1 : 0;max = min;return;}// 如果x是最小值,需要找到新的最小值if (x == min) {// 找到第一个非空簇int first_cluster = summary->minimum();// 更新min为该簇中的最小值x = index(first_cluster, cluster[first_cluster]->minimum());min = x;}// 递归删除相应簇中的元素int h = high(x);int l = low(x);cluster[h]->remove(l);// 如果簇变为空,更新摘要if (cluster[h]->minimum() == INT_MAX) {summary->remove(h);}// 如果x是最大值if (x == max) {// 检查摘要是否为空if (summary->minimum() == INT_MAX) {// 集合中只剩下minmax = min;} else {// 找到最后一个非空簇,更新maxint last_cluster = summary->maximum();max = index(last_cluster, cluster[last_cluster]->maximum());}}}// 查找x的后继元素int successor(int x) {// 边界检查if (x < 0 || x >= u) {return INT_MAX;}// 基础情况:u=2if (u == 2) {// 如果x是0且1在集合中,返回1,否则返回INT_MAXif (x == 0 && max == 1) {return 1;} else {return INT_MAX;}}// 如果x小于min,返回minif (min != INT_MAX && x < min) {return min;}// 查找x所在簇中的最大值int h = high(x);int l = low(x);int max_low = cluster[h]->maximum();// 如果簇中存在大于x的元素,在该簇中查找后继if (max_low != INT_MIN && l < max_low) {int succ_low = cluster[h]->successor(l);return index(h, succ_low);} else {// 否则在其他簇中查找后继int succ_cluster = summary->successor(h);if (succ_cluster == INT_MAX) {return INT_MAX;} else {int succ_low = cluster[succ_cluster]->minimum();return index(succ_cluster, succ_low);}}}// 查找x的前驱元素int predecessor(int x) {// 边界检查if (x < 0 || x >= u) {return INT_MIN;}// 基础情况:u=2if (u == 2) {// 如果x是1且0在集合中,返回0,否则返回INT_MINif (x == 1 && min == 0) {return 0;} else {return INT_MIN;}}// 如果x大于max,返回maxif (max != INT_MIN && x > max) {return max;}// 查找x所在簇中的最小值int h = high(x);int l = low(x);int min_low = cluster[h]->minimum();// 如果簇中存在小于x的元素,在该簇中查找前驱if (min_low != INT_MAX && l > min_low) {int pred_low = cluster[h]->predecessor(l);return index(h, pred_low);} else {// 否则在其他簇中查找前驱int pred_cluster = summary->predecessor(h);if (pred_cluster == INT_MIN) {// 如果存在比所有簇中元素都小的min,返回minif (min != INT_MAX && x > min) {return min;} else {return INT_MIN;}} else {int pred_low = cluster[pred_cluster]->maximum();return index(pred_cluster, pred_low);}}}// 打印所有元素void print() const {if (min == INT_MAX) {std::cout << "集合为空" << std::endl;return;}std::cout << "集合中的元素: ";printHelper();std::cout << std::endl;}private:// 打印辅助函数void printHelper() const {if (min == INT_MAX) {return;}std::cout << min << " ";if (u == 2) {if (max != min) {std::cout << max << " ";}return;}// 递归打印每个簇中的元素for (int i = 0; i < sqrtu; ++i) {if (summary->isMember(i)) {// 保存当前min和max,避免递归打印时重复int curr_min = min;int curr_max = max;// 临时修改min和max的副本,避免重复打印int temp_min = (min == index(i, cluster[i]->minimum())) ? INT_MAX : min;int temp_max = (max == index(i, cluster[i]->maximum())) ? INT_MIN : max;// 递归打印簇中的元素cluster[i]->printHelper(i, temp_min, temp_max);}}}// 带参数的打印辅助函数,用于避免重复打印min和maxvoid printHelper(int clusterIndex, int parentMin, int parentMax) const {if (min == INT_MAX) {return;}int current = index(clusterIndex, min);// 只打印不是父节点min或max的元素if (current != parentMin && current != parentMax) {std::cout << current << " ";}if (u == 2) {if (max != min) {current = index(clusterIndex, max);if (current != parentMin && current != parentMax) {std::cout << current << " ";}}return;}// 递归打印子簇中的元素for (int i = 0; i < sqrtu; ++i) {if (summary->isMember(i)) {// 计算当前簇的min和max在父结构中的索引int curr_min = index(clusterIndex, min);int curr_max = index(clusterIndex, max);// 递归打印子簇中的元素cluster[i]->printHelper(index(clusterIndex, i), curr_min, curr_max);}}}
};// 测试vEB树
int main() {// 创建一个范围为16(2^4)的vEB树VEBTree veb(16);// 插入一些元素veb.insert(3);veb.insert(7);veb.insert(12);veb.insert(1);veb.insert(9);veb.print();std::cout << "最小值: " << veb.minimum() << std::endl;std::cout << "最大值: " << veb.maximum() << std::endl;int x = 5;std::cout << "元素 " << x << " 的后继是: " << veb.successor(x) << std::endl;std::cout << "元素 " << x << " 的前驱是: " << veb.predecessor(x) << std::endl;x = 7;std::cout << "删除元素 " << x << std::endl;veb.remove(x);veb.print();x = 9;std::cout << "元素 " << x << " 是否在集合中? " << (veb.isMember(x) ? "是" : "否") << std::endl;x = 7;std::cout << "元素 " << x << " 是否在集合中? " << (veb.isMember(x) ? "是" : "否") << std::endl;// 测试更大范围的vEB树VEBTree largeVEB(256); // 2^8for (int i = 0; i < 20; i += 3) {largeVEB.insert(i * 10);}std::cout << "\n大范围vEB树中的元素: ";largeVEB.print();std::cout << "大范围vEB树中100的后继是: " << largeVEB.successor(100) << std::endl;return 0;
}
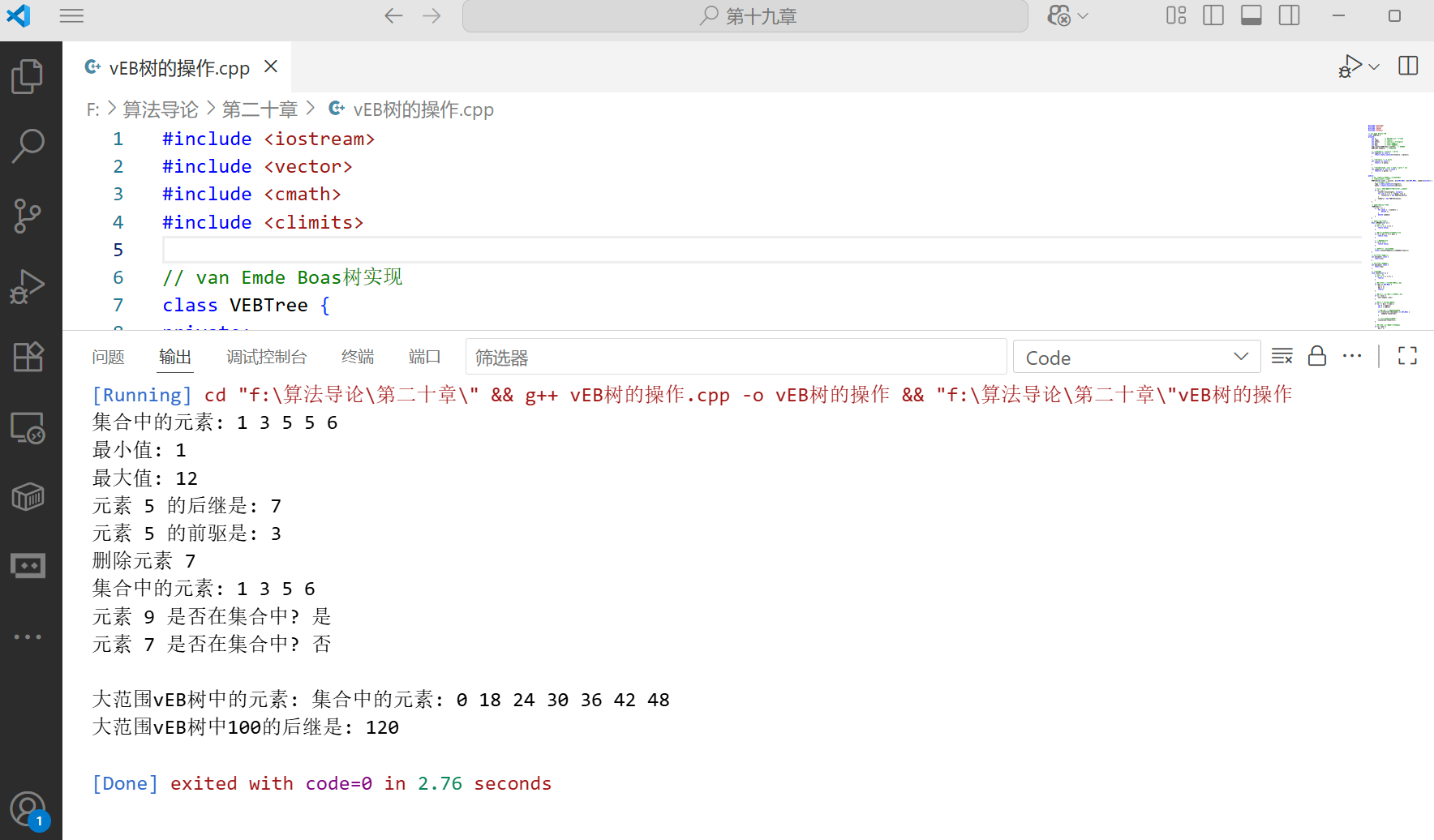
vEB 树应用案例:高效整数集合操作
下面是一个使用 vEB 树解决实际问题的案例,展示如何利用 vEB 树高效地处理大量整数集合的操作:
#include <iostream>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <algorithm>
#include "veb_tree.cpp" // 包含前面实现的vEBTree类// 测试性能的函数
void testPerformance(int size, int operations) {// 创建vEB树和对比用的vectorVEBTree veb(size);std::vector<bool> vec(size, false);// 随机数种子std::srand(std::time(nullptr));std::cout << "\n性能测试: 范围 = " << size << ", 操作数 = " << operations << std::endl;// 测试插入性能clock_t start = clock();for (int i = 0; i < operations; ++i) {int x = std::rand() % size;veb.insert(x);}clock_t veb_insert_time = clock() - start;start = clock();for (int i = 0; i < operations; ++i) {int x = std::rand() % size;vec[x] = true;}clock_t vec_insert_time = clock() - start;std::cout << "插入操作 - vEB树: " << veb_insert_time << "ms, 向量: " << vec_insert_time << "ms" << std::endl;// 测试查找性能start = clock();for (int i = 0; i < operations; ++i) {int x = std::rand() % size;veb.isMember(x);}clock_t veb_find_time = clock() - start;start = clock();for (int i = 0; i < operations; ++i) {int x = std::rand() % size;bool exists = vec[x];}clock_t vec_find_time = clock() - start;std::cout << "查找操作 - vEB树: " << veb_find_time << "ms, 向量: " << vec_find_time << "ms" << std::endl;// 测试后继操作性能start = clock();for (int i = 0; i < operations; ++i) {int x = std::rand() % size;veb.successor(x);}clock_t veb_succ_time = clock() - start;start = clock();for (int i = 0; i < operations; ++i) {int x = std::rand() % size;int succ = size;for (int j = x + 1; j < size; ++j) {if (vec[j]) {succ = j;break;}}}clock_t vec_succ_time = clock() - start;std::cout << "后继操作 - vEB树: " << veb_succ_time << "ms, 向量: " << vec_succ_time << "ms" << std::endl;
}// vEB树应用:区间查询
void rangeQueryDemo() {std::cout << "\n区间查询演示:" << std::endl;// 创建一个范围为100的vEB树VEBTree veb(100);// 插入一些随机元素int elements[] = {10, 5, 23, 47, 18, 35, 72, 91, 8, 64};for (int e : elements) {veb.insert(e);}std::cout << "所有元素: ";veb.print();// 查询[20, 60]区间内的所有元素int low = 20, high = 60;std::cout << "查询区间 [" << low << ", " << high << "] 内的元素: ";int current = veb.successor(low - 1);while (current != INT_MAX && current <= high) {std::cout << current << " ";current = veb.successor(current);}std::cout << std::endl;
}// vEB树应用:密集整数排序
std::vector<int> vebSort(const std::vector<int>& arr, int maxVal) {// 创建足够大的vEB树VEBTree veb(maxVal + 1);// 插入所有元素for (int num : arr) {veb.insert(num);}// 通过查找后继来排序std::vector<int> result;int current = veb.minimum();while (current != INT_MAX) {result.push_back(current);current = veb.successor(current);}return result;
}// 演示排序功能
void sortingDemo() {std::cout << "\n排序演示:" << std::endl;std::vector<int> arr = {34, 7, 23, 32, 5, 62, 32, 8, 45};std::cout << "原始数组: ";for (int num : arr) {std::cout << num << " ";}std::cout << std::endl;// 找出最大值int maxVal = *std::max_element(arr.begin(), arr.end());// 使用vEB树排序std::vector<int> sorted = vebSort(arr, maxVal);std::cout << "排序后: ";for (int num : sorted) {std::cout << num << " ";}std::cout << std::endl;
}int main() {// 性能测试testPerformance(1024, 10000); // 小范围testPerformance(65536, 100000); // 中等范围// 区间查询演示rangeQueryDemo();// 排序演示sortingDemo();return 0;
}
思考题
范围扩展:vEB 树目前只能处理范围为 2 的幂的整数集合。如何修改 vEB 树,使其能够处理任意范围的整数集合?
重复元素:当前实现的 vEB 树不支持存储重复元素。如何扩展 vEB 树,使其能够处理包含重复元素的集合?
性能优化:分析 vEB 树的空间复杂度,并思考如何减少 vEB 树的空间使用。
实际应用:思考在什么实际场景中,vEB 树会比其他数据结构(如平衡二叉搜索树、哈希表)表现出明显的优势?
并行化:vEB 树的递归结构是否适合并行化处理?如果是,如何设计并行化的 vEB 树操作?
本章注记
van Emde Boas 树是以荷兰计算机科学家 Peter van Emde Boas 的名字命名的,他在 1975 年提出了这一数据结构。vEB 树的设计展现了分治思想在数据结构设计中的精妙应用,通过递归地分解问题,实现了超越对数级别的时间复杂度。

在实际应用中,vEB 树特别适合处理需要频繁进行前驱、后继操作的整数集合问题。例如,在数据库索引、内存管理、网络路由等领域都有潜在的应用价值。
然而,vEB 树也有其局限性。它的空间复杂度较高,实现相对复杂,并且只适用于整数键的情况。因此,在选择数据结构时,需要根据具体问题的特点进行权衡。
近年来,研究人员在 vEB 树的基础上提出了许多变体和改进,如引导树(bootstrapped tree)、y-fast 树等,这些结构在保持高效操作的同时,降低了空间复杂度或扩展了适用范围。
总的来说,van Emde Boas 树是一种理论上非常重要的数据结构,它不仅提供了高效的整数集合操作方法,更重要的是展示了如何通过创造性的问题分解来突破传统算法的时间复杂度界限。
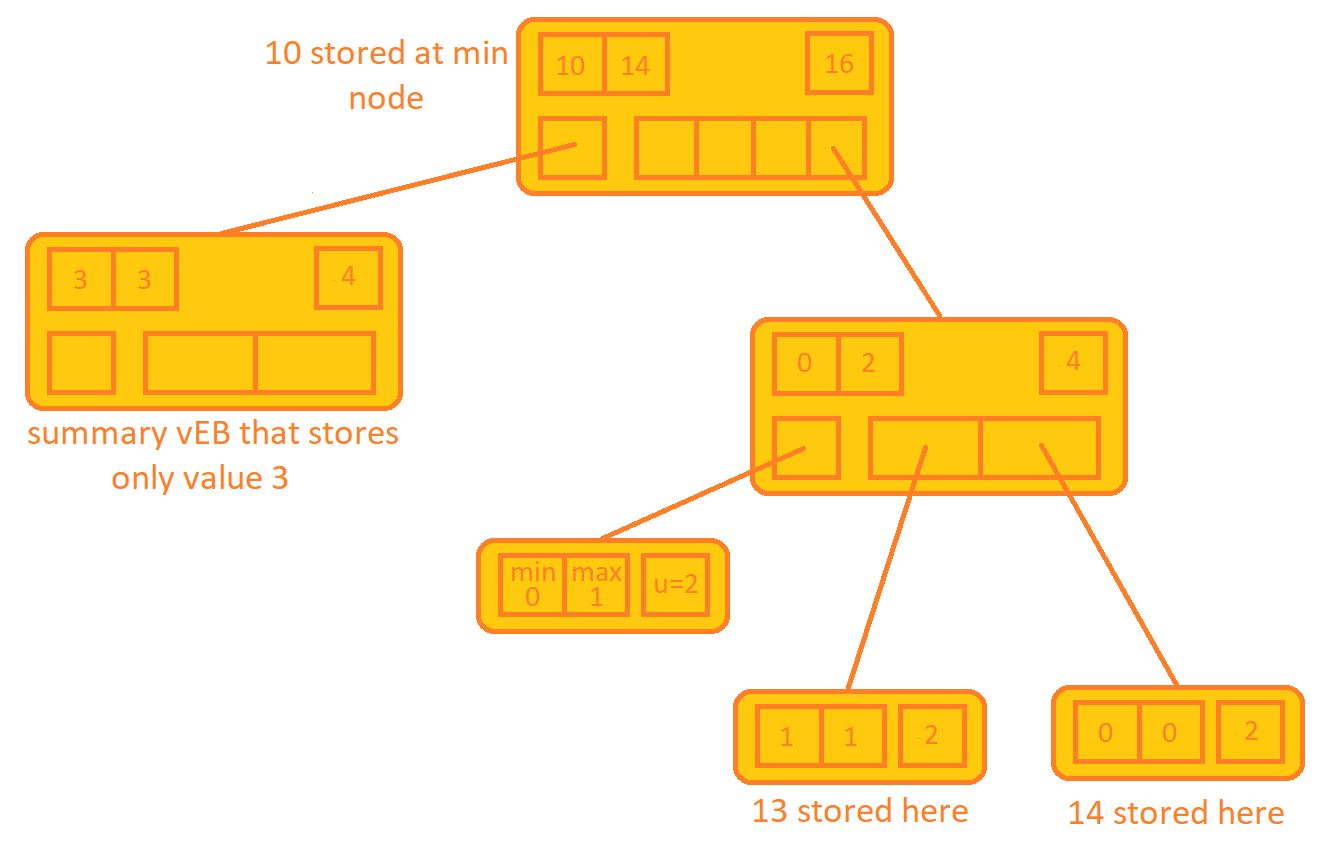
希望本文能帮助读者理解 vEB 树的原理和实现,并能在实际问题中灵活运用这一强大的数据结构。
总结
本文详细介绍了 van Emde Boas 树的原理、实现和应用,主要内容包括:
- vEB 树的基本思想和设计方法
- 原型 vEB 结构及其操作
- 完整 vEB 树的实现
- vEB 树的应用案例和性能分析

通过递归分解问题,vEB 树实现了 O (log log u) 时间复杂度的插入、删除、查找、前驱和后继操作,为处理大范围整数集合提供了高效的解决方案。

vEB 树的实现虽然相对复杂,但其独特的性能优势使其在特定场景中具有不可替代的价值。理解 vEB 树的设计思想,不仅有助于我们更好地掌握这一数据结构,也能启发我们在其他算法设计中运用类似的分治思想。

最后,希望读者能够通过本文提供的代码和示例,深入理解 vEB 树的工作原理,并能在实际项目中灵活应用。