当前位置：首页 > news >正文

【C++竞赛】核桃CSP-J模拟赛题解

news 2025/8/12 13:49:12

第一题：P10479 快乐数

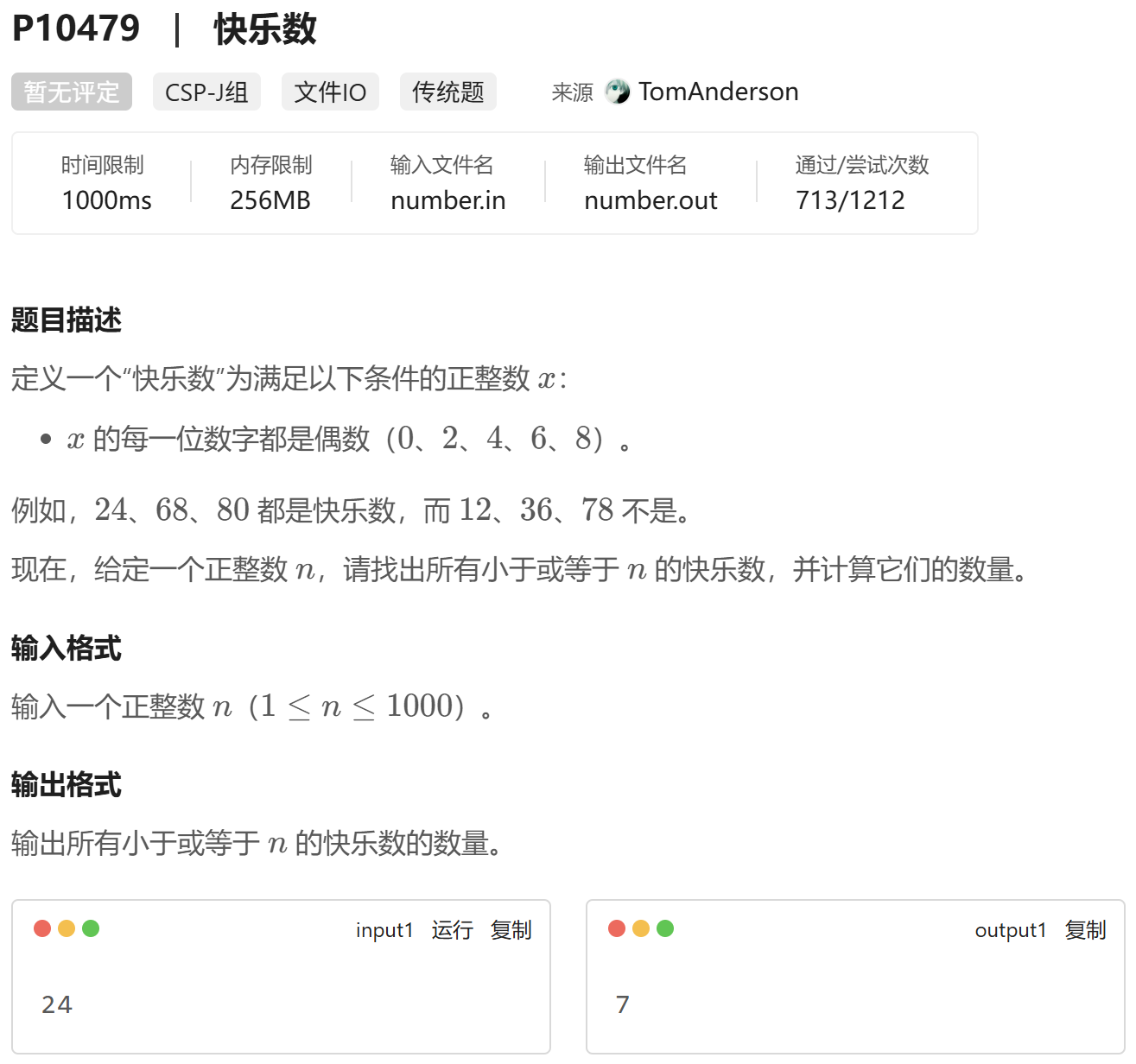
题目回顾：

在这里插入图片描述

题解：

题目分析

题目要求找出所有小于或等于给定正整数 $n$ 的“快乐数”。快乐数的定义是：该数的每一位数字都是偶数（即 0、2、4、6、8）。例如，24、68、80 是快乐数，而 12、36、78 不是。

解题思路

检查快乐数：编写一个辅助函数 HappyNum，该函数接受一个整数，检查其每一位数字是否都是偶数。
- 通过循环取出该数的每一位数字（使用取模 10 运算）。
- 如果发现任何一位数字是奇数，则返回 false；如果所有位都是偶数，则返回 true。
遍历所有数：在主函数中，从 1 到 $n$ 遍历每个整数，使用 HappyNum 函数判断是否为快乐数。
计数：统计所有快乐数的个数并输出。

代码实现

#include <bits/stdc++.h>
using namespace std;bool HappyNum(int n) {while (n > 0) {int d = n % 10;      // 取出最后一位数字if (d % 2 != 0) {    // 检查是否为奇数return false;}n /= 10;             // 去掉最后一位}return true;
}int main() {freopen("number.in", "r", stdin);    // 文件输入freopen("number.out", "w", stdout);  // 文件输出int n;cin >> n;int cnt = 0;             // 计数器，记录快乐数的个数for (int i = 1; i <= n; ++i) {if (HappyNum(i)) {   // 检查当前数是否为快乐数++cnt;}}cout << cnt << endl;     // 输出结果return 0;
}

代码说明

HappyNum 函数：
- 通过循环逐位检查数字的每一位。
- 若发现奇数位，立即返回 false；若所有位均为偶数，返回 true。
主函数：
- 重定向输入输出至指定文件（number.in 和 number.out）。
- 读取整数 $(n)$ 。
- 遍历 1 到 $n$ 的所有整数，使用 HappyNum 判断是否为快乐数，并计数。
- 输出最终计数结果。

复杂度分析

时间复杂度： $\log n)$ 。遍历 $(n)$ 个数，每个数的检查需要 $O(log⁡n)O(\log n)$ 时间（数字的位数）。
空间复杂度： $O (1)$ 。仅使用常数级别的额外空间。

示例测试

输入：10
输出：4（快乐数为 2、4、6、8）
输入：20
输出：5（快乐数为 2、4、6、8、20）

该解法直接高效，适用于题目给定的数据范围 $\leq n \leq 1000$ 。

第二题：P10480 谷子商店

题目回顾：

在这里插入图片描述

题解：

题目分析

题目要求计算购买谷子袋的方案数，使得购买后能集齐所有种类的谷子。给定 m 个谷子袋，每个袋子包含若干种谷子（种类编号 1~n）。需要找出所有选择袋子的组合，使得这些袋子中谷子的并集覆盖全部 n 种谷子。

解题思路

状态压缩：由于 n 和 m 最大为 10，可以使用二进制位表示谷子种类和袋子选择方案。
- 每个袋子用一个整数表示，该整数的二进制位表示袋子包含的谷子种类（例如，种类 g 对应第 (g-1) 位为 1）。
枚举所有方案：遍历所有可能的袋子选择方案（共 2^m 种）。
- 对于每个方案，计算所选袋子中谷子种类的并集（通过按位或运算实现）。
检查完整性：判断并集是否包含所有 n 种谷子（即是否等于 2^n - 1）。
计数：统计满足条件的方案数量。

代码实现

#include <bits/stdc++.h>
using namespace std;int main() {freopen("goods.in", "r", stdin);freopen("goods.out", "w", stdout);int n, m;cin >> n >> m;vector<int> bags(m, 0);  // 存储每个袋子的谷子信息（二进制表示）for (int i = 0; i < m; ++i) {int N;cin >> N;for (int j = 0; j < N; ++j) {int g;cin >> g;bags[i] |= (1 << (g - 1));  // 设置对应种类位}}int fullSet = (1 << n) - 1;  // 全集（n 位全 1）int count = 0;// 枚举所有袋子选择方案 (0 到 2^m - 1)for (int mask = 0; mask < (1 << m); ++mask) {int currentSet = 0;for (int i = 0; i < m; ++i) {if (mask & (1 << i)) {  // 检查是否选择第 i 个袋子currentSet |= bags[i];  // 合并谷子种类}}if (currentSet == fullSet) {count++;  // 满足条件则计数}}cout << count << endl;return 0;
}

代码说明

输入处理：
- 读取谷子种类数 n 和袋子数量 m。
- 对于每个袋子，读取其中谷子的数量和种类，并用二进制位表示（种类 g 对应第 (g-1) 位）。
全集计算：
- fullSet = (1 << n) - 1 表示所有谷子种类的集合（低 n 位全为 1）。
枚举方案：
- 外层循环枚举所有袋子选择方案（mask 的二进制位表示选择哪些袋子）。
- 内层循环检查每个袋子是否被选中，如果选中则将其谷子集合合并到当前集合中。
结果检查：
- 如果当前集合等于全集，则方案有效，计数器加 1。
输出结果：
- 输出满足条件的方案总数。