逐际动力开源运控 tron1-rl-isaacgym 解读与改进
文章目录
- 概览
- 基础框架解读
- 线速度估计
- 观测结构
- 仿真实验
- 点足式步态设计
- 步态相位与接触状态建模
- 步态接触奖励
- 动作延迟
- 我的改进
- Point-goal Locomotion
- 观测修改
- 奖励修改
- 预训练地形编码器
- Sliced Wasserstein AutoEncoder
- 模型训练与结果
- 参考材料
概览
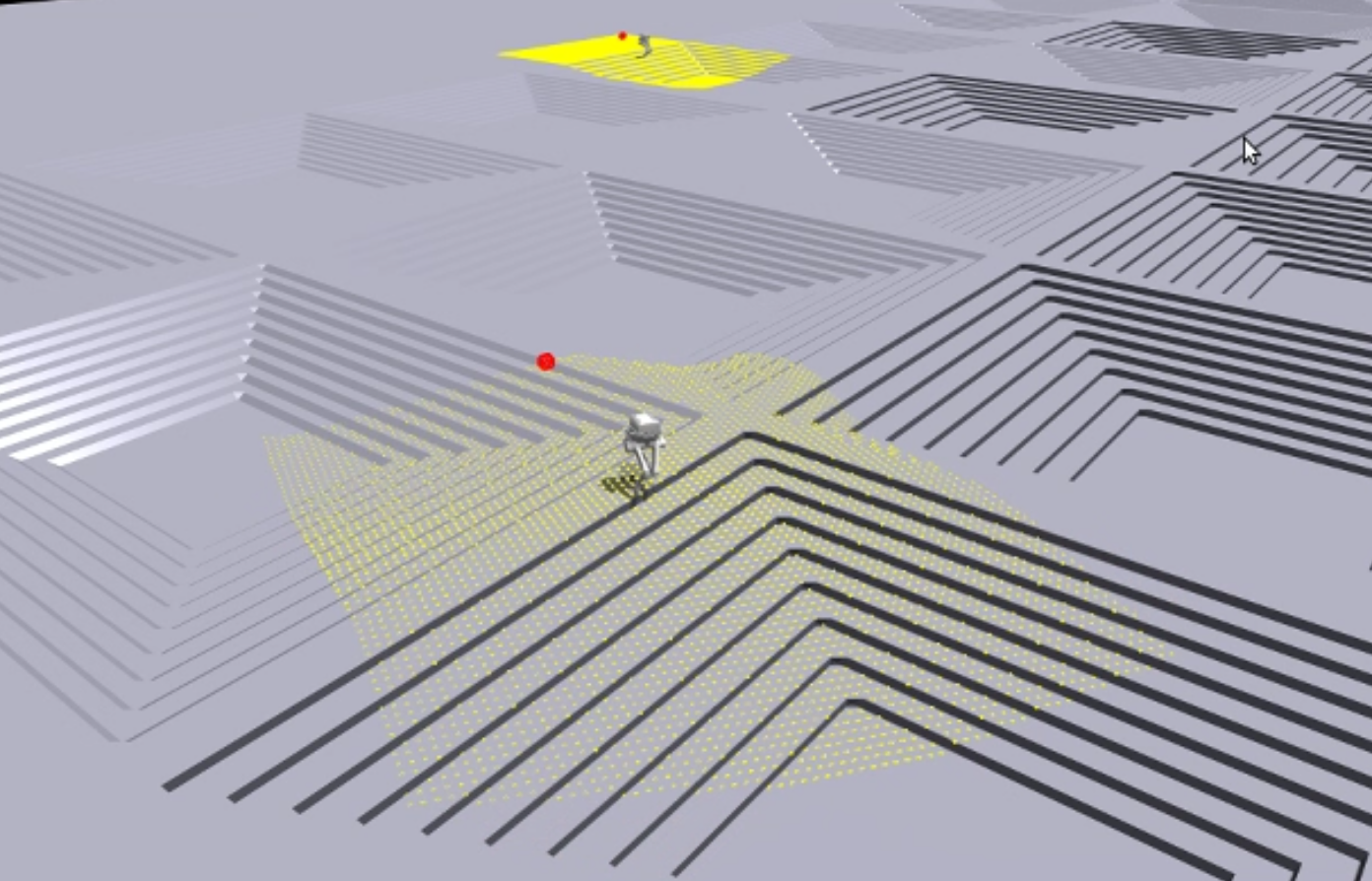
这篇博客记录了我参加逐际动力创学营2025期间的技术总结。
传送门:逐际动力开源运控 tron1-rl-isaacgym:https://github.com/limxdynamics/tron1-rl-isaacgym
项目基于legged_gym框架进行开发,主要对envs(环境)和algorithm(算法)模块进行了修改。其中,algorithm部分基于rsl-rl改造,envs模块则采用了一个环境对应一个机器人任务配置的设计方案。本文将重点介绍点足式机器人的相关内容。下面是框架的整体流程图。
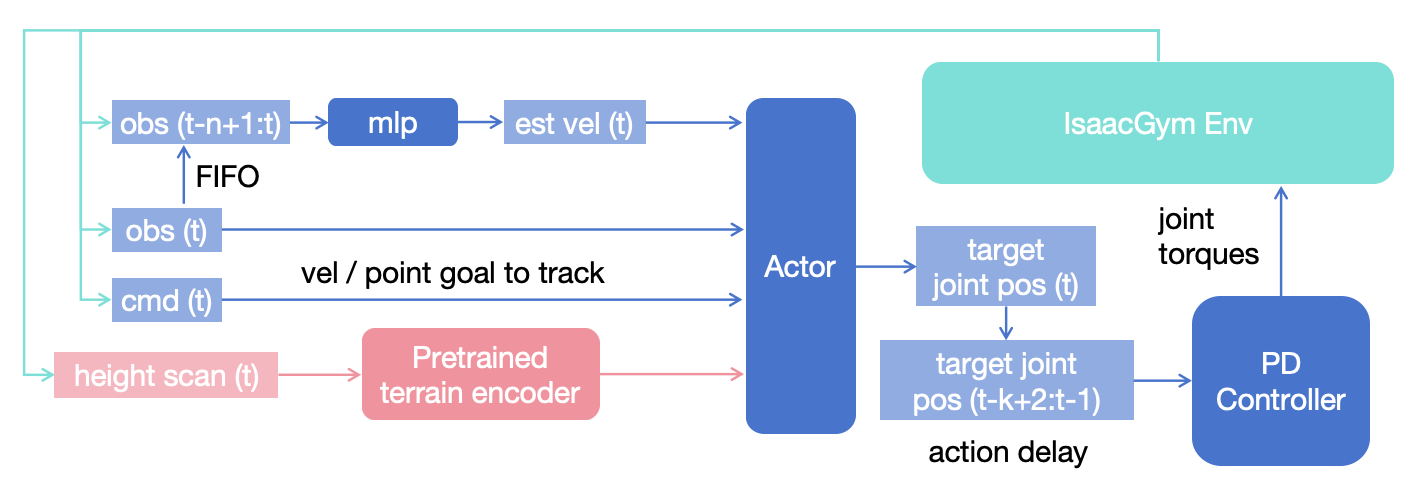
基础框架解读
线速度估计
观测结构
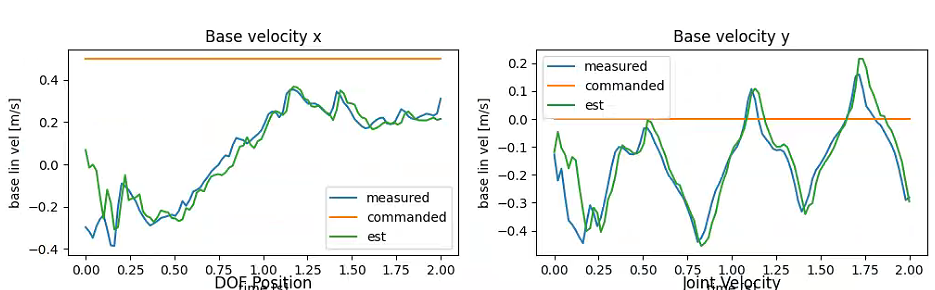
与legged_gym不同的是,在compute_group_observations函数中,移除了环境观测obs_buf的线速度信息。这是因为直接获取线速度存在较大难度且噪声干扰严重,通常需要通过SLAM或状态估计技术才能准确获得。该框架采用状态估计方法,通过一个MLP网络来估计线速度。网络的输入是连续n帧的观测数据,输出为3维线速度估计值。Actor网络的最终输入由三部分组成:torch.cat((est, obs, commands)),即估计线速度、当前帧观测数据和速度跟踪指令。为了计算损失函数,在critic观测数据的最前面加入了从仿真器获取的线速度真值base_lin_vel。
- Actor 观测量
obs_buf组成
| 顺序 | 张量 | 维度 | 缩放因子 | 含义 |
|---|---|---|---|---|
| 1 | base_ang_vel | 3 | obs_scales.ang_vel | 机身角速度(rad/s) |
| 2 | projected_gravity | 3 | — | 重力在机身坐标系下的投影 |
| 3 | (dof_pos - default_dof_pos) | 6 | obs_scales.dof_pos | 关节位置偏差 |
| 4 | dof_vel | 6 | obs_scales.dof_vel | 关节速度 |
| 5 | actions | 6 | — | 上一步动作(关节目标) |
| 6 | clock_inputs_sin.view(num_envs, 1) | 1 | — | 步态时钟输入:sin 分量 |
| 7 | clock_inputs_cos.view(num_envs, 1) | 1 | — | 步态时钟输入:cos 分量 |
| 8 | gaits | 4 | — | 当前步态参数(频率、相位偏移、占空比等) |
- Critic 观测量
critic_obs_buf组成
| 顺序 | 张量 | 维度 | 缩放因子 | 含义 |
|---|---|---|---|---|
| 1 | base_lin_vel | 3 | obs_scales.lin_vel | 机身线速度(m/s) |
| 2 | obs_buf | 30 | — | 上表中的 Actor 观测量 |
在机器人任务中,关节速度、位置和步态信息的时序演变隐含着机器人的构型及正逆运动学(IK)特征。以往我们在使用观测值堆叠或LSTM/GRU等时序模型时,往往不会过多关注最终输出向量的物理含义(特别是在游戏类决策环境中),但机器人任务为此提供了良好的切入点。
仿真实验
如图所示,仿真效果相当理想。
点足式步态设计
我们整合了步态时钟与步态参数指标的观测数据,各参数定义如下:
- 步频 fff
- 相位偏移量 δ\deltaδ
- 占空比 ddd:一周期中有 ddd 的比例处于支撑
- 抬腿高度(似乎没用到)
步态相位与接触状态建模
对应框架中的(
_step_contact_targets函数)
这一过程可理解为:通过调整正弦/余弦函数的形态,使其与期望的接触状态随时间变化的规律相匹配,从而实现跟踪目标。
i. 步态相位(时钟)更新
ϕt+1=(ϕt+Δt⋅f)mod1\phi_{t+1} = (\phi_t + \Delta t \cdot f) \bmod 1 ϕt+1=(ϕt+Δt⋅f)mod1
离散时间里用频率 fff(Hz)推进相位;取模把相位限制在 [0,1)[0,1)[0,1) 的单位圆上。等价的连续形式是 ϕ˙=f\dot{\phi} = fϕ˙=f。这样能稳定地产生严格周期的时钟信号。
ii. 左右脚相位关系
ϕL=(ϕ)mod1,ϕR=(ϕ+δ+1)mod1\phi_L = (\phi) \bmod 1, \qquad \phi_R = (\phi + \delta + 1) \bmod 1 ϕL=(ϕ)mod1,ϕR=(ϕ+δ+1)mod1
典型取值:小跑/对角步常用 δ≈0.5\delta \approx 0.5δ≈0.5。
iii. 足部状态判定
state(ϕi)={stance(支撑),ϕi<dswing(摆动),ϕi≥d\text{state}(\phi_i) = \begin{cases} \text{stance(支撑)}, & \phi_i < d\\[2pt] \text{swing(摆动)}, & \phi_i \ge d \end{cases} state(ϕi)={stance(支撑),swing(摆动),ϕi<dϕi≥d
走路常用 d>0.5d > 0.5d>0.5(着地更久),跑步常用 d<0.5d < 0.5d<0.5。
iv. 归一化相位(支撑/摆动映射到固定半周期)
ϕ′(ϕ)={ϕstance′=ϕd⋅0.5,ϕ<dϕswing′=0.5+ϕ−d1−d⋅0.5,ϕ≥d\phi'(\phi) = \begin{cases} \displaystyle \phi'_{\text{stance}} = \frac{\phi}{d} \cdot 0.5, & \phi < d\\[10pt] \displaystyle \phi'_{\text{swing}} = 0.5 + \frac{\phi - d}{1 - d} \cdot 0.5, & \phi \ge d \end{cases} ϕ′(ϕ)=⎩⎨⎧ϕstance′=dϕ⋅0.5,ϕswing′=0.5+1−dϕ−d⋅0.5,ϕ<dϕ≥d
把原相位区间 [0,d)[0,d)[0,d)(支撑)线性压缩到 [0,0.5)[0,0.5)[0,0.5);把 [d,1)[d,1)[d,1)(摆动)线性压缩到 [0.5,1)[0.5,1)[0.5,1)。
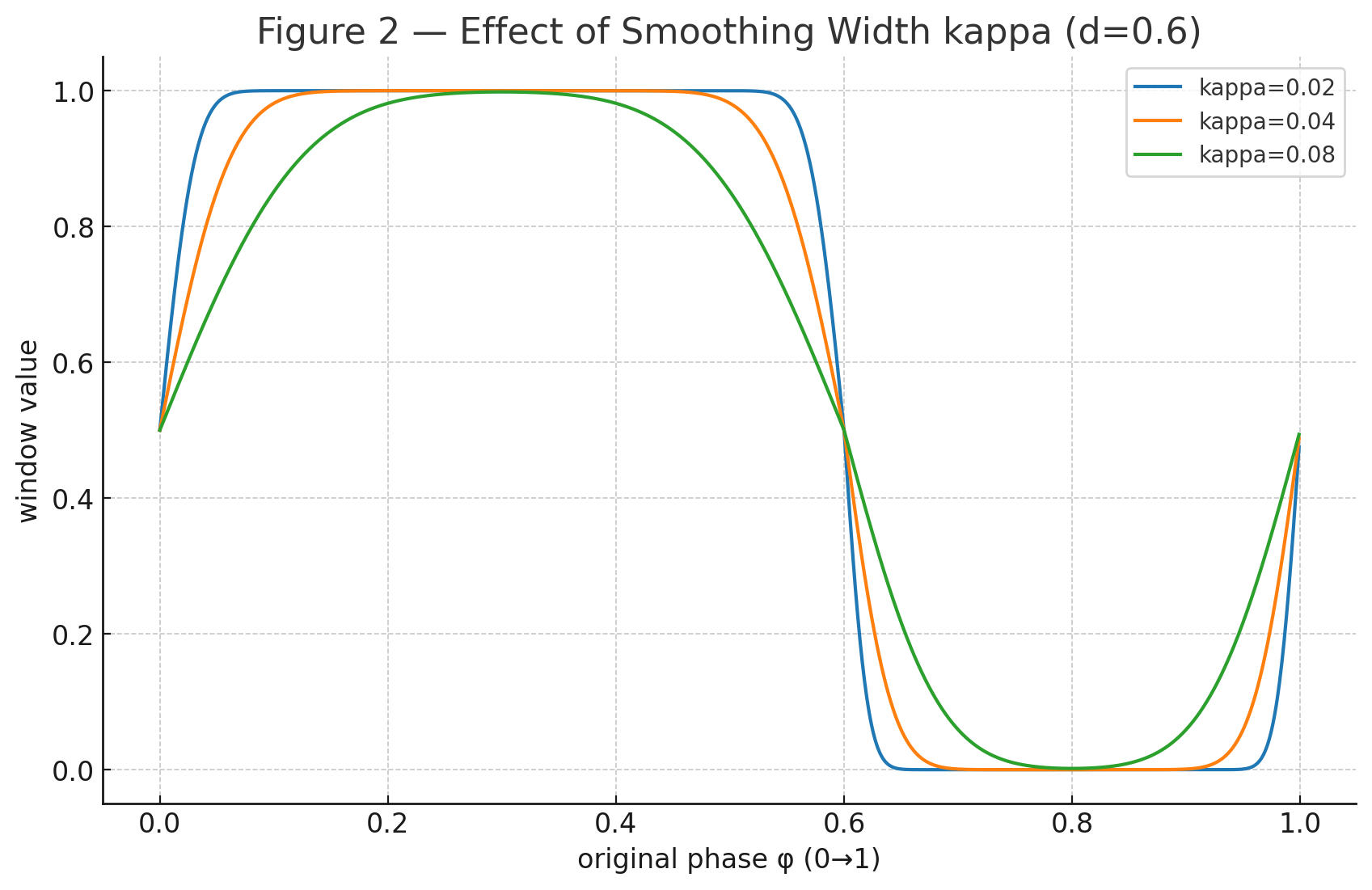
v. 平滑过渡与周期窗函数
把“是否接触”从硬 0/10/10/1 变成连续平滑的概率/强度,既能做模仿/奖励加权,也能作为控制器的软目标,减少硬切换带来的震荡。
Φκ(x)=12[1+erf(xκ2)]\Phi_\kappa(x) = \frac{1}{2} \left[1 + \operatorname{erf} \left( \frac{x}{\kappa \sqrt{2}} \right) \right] Φκ(x)=21[1+erf(κ2x)]
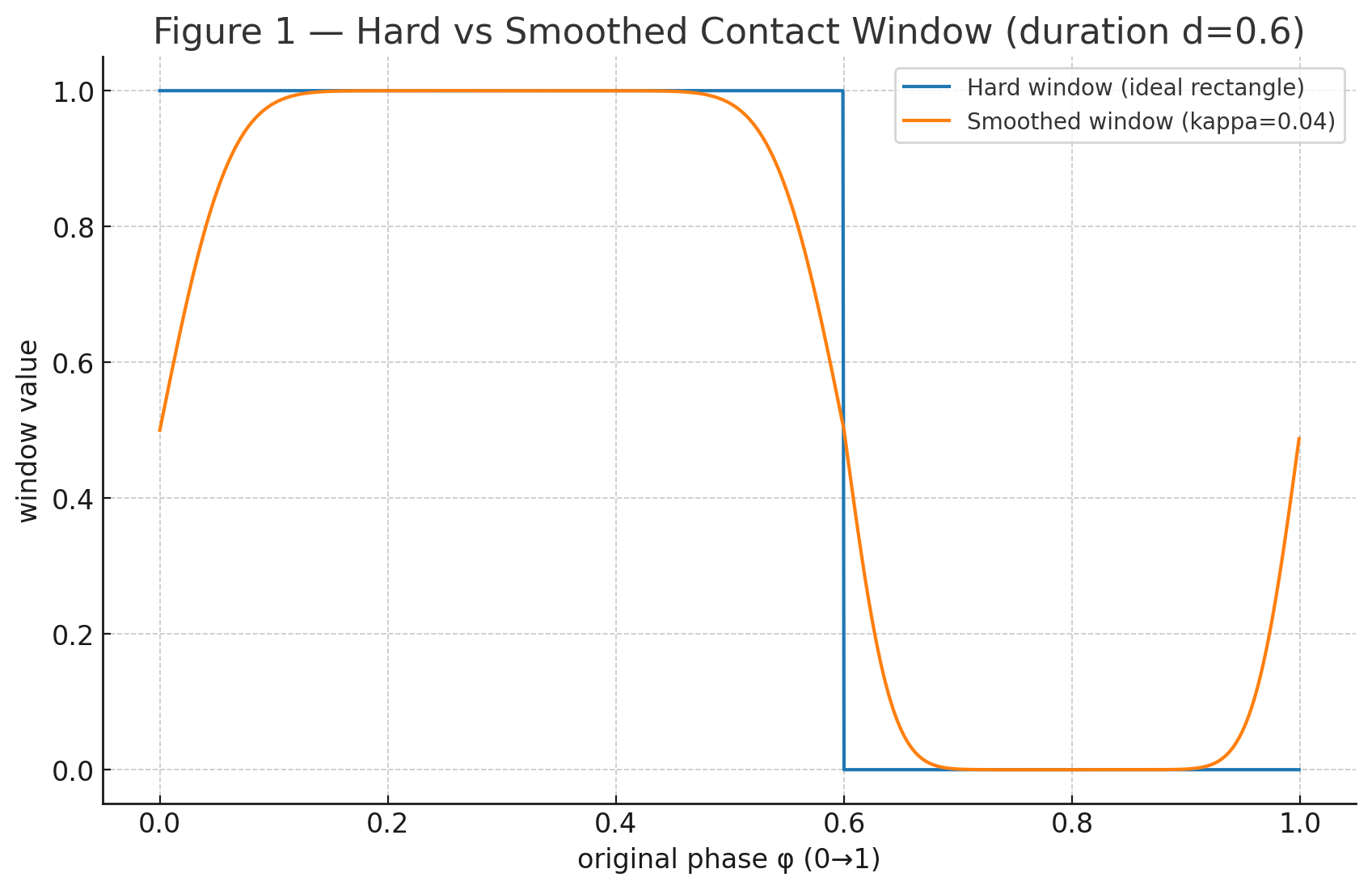
S(ϕ′)=Φκ(ϕ′)[1−Φκ(ϕ′−0.5)]+Φκ(ϕ′−1)[1−Φκ(ϕ′−1.5)]S(\phi') = \Phi_\kappa(\phi') \, [1 - \Phi_\kappa(\phi' - 0.5)] \;+\; \Phi_\kappa(\phi' - 1) \, [1 - \Phi_\kappa(\phi' - 1.5)] S(ϕ′)=Φκ(ϕ′)[1−Φκ(ϕ′−0.5)]+Φκ(ϕ′−1)[1−Φκ(ϕ′−1.5)]
-
Φκ\Phi_\kappaΦκ 是平滑阶跃(正态 CDF),κ\kappaκ 控制边界软硬:κ↓\kappa \downarrowκ↓ 接近硬开关;κ↑\kappa \uparrowκ↑ 过渡更柔和,利于稳定训练/控制,如图所示
-
第一项近似选择 ϕ′∈(0,0.5)\phi' \in (0,0.5)ϕ′∈(0,0.5) 的矩形窗,但上下沿平滑可微;
-
第二项是周期补偿(wrap-around insurance),防止 ϕ′\phi'ϕ′ 接近 111 时窗函数断裂。若已保证 ϕ′∈[0,1)\phi' \in [0,1)ϕ′∈[0,1),该项通常接近 0,可省略。
步态接触奖励
对应框架中的(
_reward_tracking_contacts_shaped_force/vel函数)
我们前面定义了接触状态的时间窗口,然后可以对不同接触状态进行观测,包括接触力和接触点速度。这两种物理量采用相同的奖励结构进行约束。
- Xi=FiX_i = F_iXi=Fi(接触力的模长)
- Xi=ViX_i = V_iXi=Vi(接触点的速度模长,通常取水平速度)
奖励函数结构
-
正向奖励模式(鼓励目标行为)
R+=∑i=1NfeetMi⋅exp(−Xi2σX2)R^+ = \sum_{i=1}^{N_{\text{feet}}} M_i \cdot \exp\left(-\frac{X_i^2}{\sigma_X^2}\right) R+=i=1∑NfeetMi⋅exp(−σX2Xi2) -
惩罚模式(抑制错误行为)
R−=∑i=1NfeetMi⋅(1−exp(−Xi2σX2))R^- = \sum_{i=1}^{N_{\text{feet}}} M_i \cdot \left(1 - \exp\left(-\frac{X_i^2}{\sigma_X^2}\right)\right) R−=i=1∑NfeetMi⋅(1−exp(−σX2Xi2))
其中:
- NfeetN_{\text{feet}}Nfeet:机器人足的数量
- XiX_iXi:被监控的物理量(力或速度)
- σX\sigma_XσX:尺度系数,控制敏感度
- MiM_iMi:接触状态掩码项
- 对接触力奖励:Mi=1−SiM_i = 1 - S_iMi=1−Si(只关心腾空相的脚)
- 对接触速度奖励:Mi=SiM_i = S_iMi=Si(只关心支撑相的脚)
物理意义
-
接触力奖励:
- 腾空相脚(Si≈0S_i \approx 0Si≈0)→ Mi≈1M_i \approx 1Mi≈1,接触力 FiF_iFi 越小,奖励越高;
- 支撑相脚(Si≈1S_i \approx 1Si≈1)→ Mi≈0M_i \approx 0Mi≈0,不参与计算。
→ 鼓励离地脚真正离地、轻盈抬起。
-
接触速度奖励:
- 支撑相脚(Si≈1S_i \approx 1Si≈1)→ Mi≈1M_i \approx 1Mi≈1,速度 ViV_iVi 越小,奖励越高;
- 腾空相脚(Si≈0S_i \approx 0Si≈0)→ Mi≈0M_i \approx 0Mi≈0,不参与计算。
→ 鼓励支撑脚稳固踩地,不滑动。
动作延迟
在将环境建模为MDP(马尔可夫决策过程)时,本质上忽略了真实环境中的异步特性,如通信延迟、执行延迟和网络推理延迟等关键因素。实际上,环境状态的动态演变不仅由step函数触发。为此,需要通过sim-to-sim方法在MuJoCo环境中进行二次验证。
为提高训练鲁棒性,可采用随机动作延迟技术(域随机化)。具体实现是,构建一个先进先出队列来执行目标位置序列。
我的改进
Point-goal Locomotion
该部分主要借鉴了eth-rsl团队在《Advanced skills by learning locomotion and local navigation end-to-end》中的工作。传统方法通常将导航问题分解为路径规划、路径跟随和运动控制等子任务,这要求机器人具备精确跟踪指令速度的运动控制能力,但在复杂机器人构型和复杂地形环境下往往难以实现。
为此,《Advanced skills》提出采用端到端的策略训练方法来解决整个导航问题:不同于持续跟踪预设路径,机器人只需在规定时间内到达目标位置即可。任务完成度仅在回合结束时进行评估,这使得策略不必追求最快到达目标,而可以自主选择行进路线和步态。这种训练方式拓展了解空间,使机器人能够掌握更复杂的运动行为。
观测修改
将原本的目标速度、角速度改为一个机器人坐标系下的目标点即可。目标点被随机设定在距离机器人初始位置2到8米之间的范围内。
奖励修改
移除原本的速度跟踪的奖励函数包括_reward_tracking_lin_vel函数以及_reward_tracking_ang_vel函数,增加下面的点跟踪奖励函数。
i. 导航任务奖励( _reward_navigation_task 函数)
rtask={1Tr⋅11+∥xb−xb∗∥2,t>T−Tr0,otherwiser_{\text{task}} = \begin{cases} \displaystyle \frac{1}{T_r}\cdot \frac{1}{1+\|x_b - x_b^{*}\|^2}, & t > T - T_r \\ 0, & \text{otherwise} \end{cases} rtask=⎩⎨⎧Tr1⋅1+∥xb−xb∗∥21,0,t>T−Trotherwise
xbx_bxb 表示当前机身位置(x,yx,yx,y),xb∗x_b^{*}xb∗ 表示目标位置,TTT 为最大回合时长,TrT_rTr 为奖励时间窗长度,ttt 为当前回合已运行时间。该奖励在末尾 TrT_rTr 时间窗内生效,值随与目标的距离减小而增大,最大可达 1/Tr1/T_r1/Tr。为了让策略学会在到达目标后稳定停住,而不是“最后一跳”冲过去,TrT_rTr 需要设置得足够长。
ii. 导航辅助奖励( _reward_navigation_bias 函数)
rbias=x˙b⋅(xb∗−xb)∥x˙b∥∥xb∗−xb∥r_{\text{bias}} = \frac{\dot{x}_b \cdot (x_b^{*} - x_b)} {\|\dot{x}_b\| \, \|x_b^{*} - x_b\|} rbias=∥x˙b∥∥xb∗−xb∥x˙b⋅(xb∗−xb)
x˙b\dot{x}_bx˙b 表示当前机身线速度,xb∗−xbx_b^{*} - x_bxb∗−xb 表示指向目标的向量。该奖励通过计算速度方向与目标方向的余弦相似度来引导策略,仅在速度与目标方向的范数均大于阈值时计算,以避免除零问题。
实际实现仅考虑机器人沿x轴正方向的速度,使其掌握面向目标点前进的运动模式。
当 mean(r_task) 达到 bias_removal_threshold * max_task_reward(论文默认 50%)时,该奖励会被移除,从而在训练早期引导机器人朝目标方向探索,达到一定主任务表现后不再束缚最终策略。
iii. 停滞惩罚( _reward_stalling_penalty函数)
rstall={−1,∥x˙b∥<0.1m/s and ∥xb−xb∗∥>0.5m0,otherwiser_{\text{stall}} = \begin{cases} -1, & \|\dot{x}_b\| < 0.1~\text{m/s} \ \text{and} \ \|x_b - x_b^{*}\| > 0.5~\text{m} \\ 0, & \text{otherwise} \end{cases} rstall={−1,0,∥x˙b∥<0.1 m/s and ∥xb−xb∗∥>0.5 motherwise
该逻辑会检查机器人速度是否小于 0.1 m/s 且离目标距离大于 0.5 m,若满足条件则给予 -1 惩罚。这样可以防止策略利用 PPO 的折扣因子在远离目标时长时间停滞,将负惩罚推迟到回合末,从而抑制“最后一刻冲刺”的行为。
预训练地形编码器
我们整合了Local planner与Locomotion policy,相比单一Locomotion policy需要更全面的高程信息支持。为此,我将原框架9×13分辨率(0.1m网格)扩展为64×64网格,覆盖6.4m×6.4m的局部地形范围,显著提升了导航规划能力。
为高效处理这些高程数据,我参考了《Terrain-attentive learning for efficient 6-DoF kinodynamic modeling on vertically challenging terrain》论文中提出的TAL方法,采用基于Sliced Wasserstein AutoEncoder的核心模型,通过自监督学习预先训练地形特征编码器。
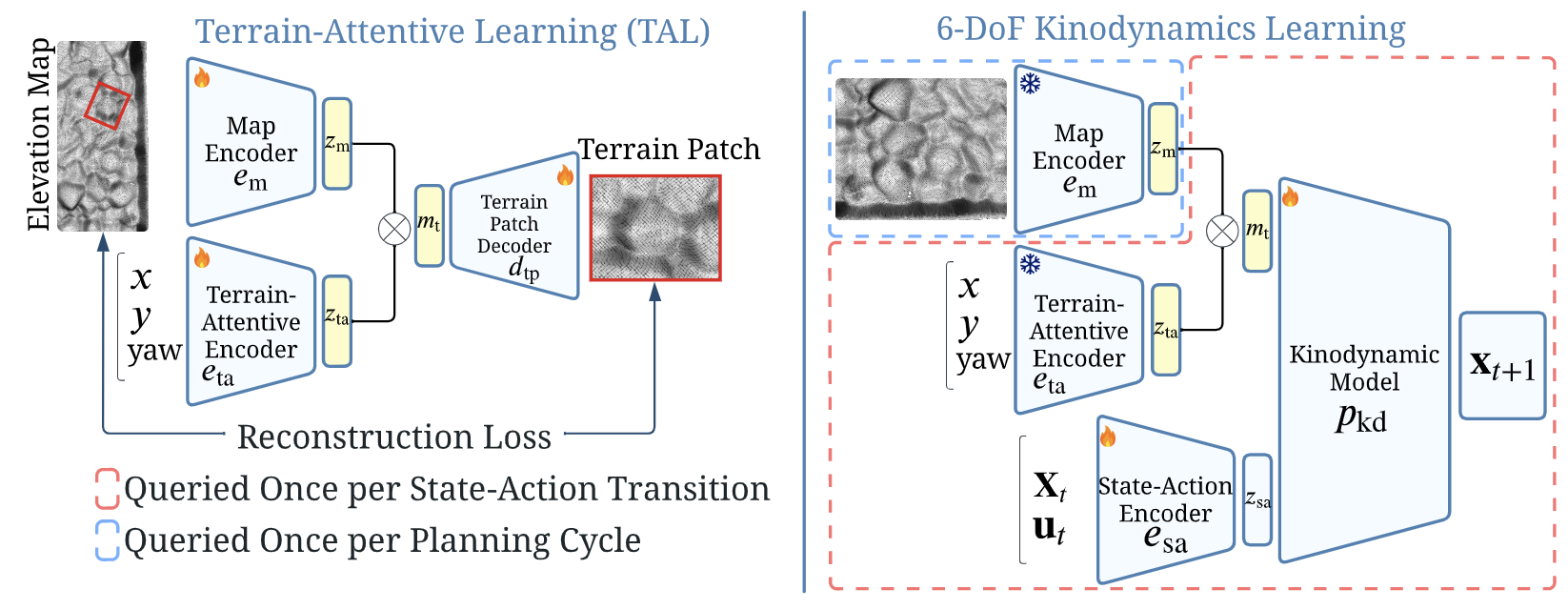
Sliced Wasserstein AutoEncoder
SWAE 属于一种改进的变分自编码器(VAE)结构,其核心思想是:
通过编码器将输入映射到潜在空间,再用解码器重构,同时用 切片 Wasserstein 距离(SWD)来约束潜在分布接近先验分布。
i. 编码过程
- 输入为二维图像数据
- 通过多层卷积运算提取特征,并逐步降低空间分辨率、增加通道数
- 将最终的高维特征展平成向量
- 用线性映射得到潜在表示向量 z∈Rdz\in \mathbb{R}^dz∈Rd
ii. 解码过程
- 将潜在向量 zzz 通过线性映射还原为卷积特征图的形状
- 通过多层反卷积逐步上采样,恢复空间分辨率
- 输出层使用双曲正切函数,将像素值约束在 [-1, 1] 区间
iii. 切片 Wasserstein 距离(SWD)正则化
- 目标:使潜在分布 q(z)q(z)q(z) 接近先验分布 p(z)p(z)p(z)(通常是标准正态分布)
- 方法:
- 在潜在空间随机采样多个方向向量 {uk}k=1K\{u_k\}_{k=1}^K{uk}k=1K,并归一化
- 将样本投影到这些方向:
πk(z)=z⋅uk\pi_k(z) = z \cdot u_k πk(z)=z⋅uk - 对投影结果排序,并与先验分布投影结果一一对应
- 计算排序后两组投影的 p-范数距离
- 对所有方向的距离取平均,得到 SWD 值:
SWD=1K∑k=1K∥sort(πk(z))−sort(πk(z′))∥p\text{SWD} = \frac{1}{K} \sum_{k=1}^K \| \text{sort}(\pi_k(z)) - \text{sort}(\pi_k(z')) \|_p SWD=K1k=1∑K∥sort(πk(z))−sort(πk(z′))∥p
其中 z′∼p(z)z' \sim p(z)z′∼p(z)
iv. 损失函数
L=L重构误差+λSWD⋅SWD\mathcal{L} = \mathcal{L}_{\text{重构误差}} + \lambda_{\text{SWD}} \cdot \text{SWD} L=L重构误差+λSWD⋅SWD
其中重构误差可以是 L1L_1L1 或 L2L_2L2 范数。
模型训练与结果
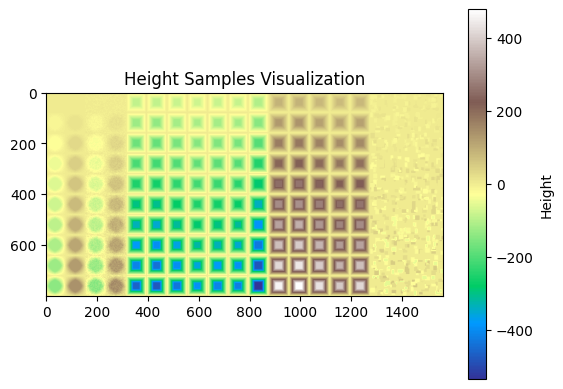
如图所示,保存框架中地形课程的全部地形数据,基于原框架中_get_heights和_init_height_points函数的高程点采样逻辑构建训练数据集。
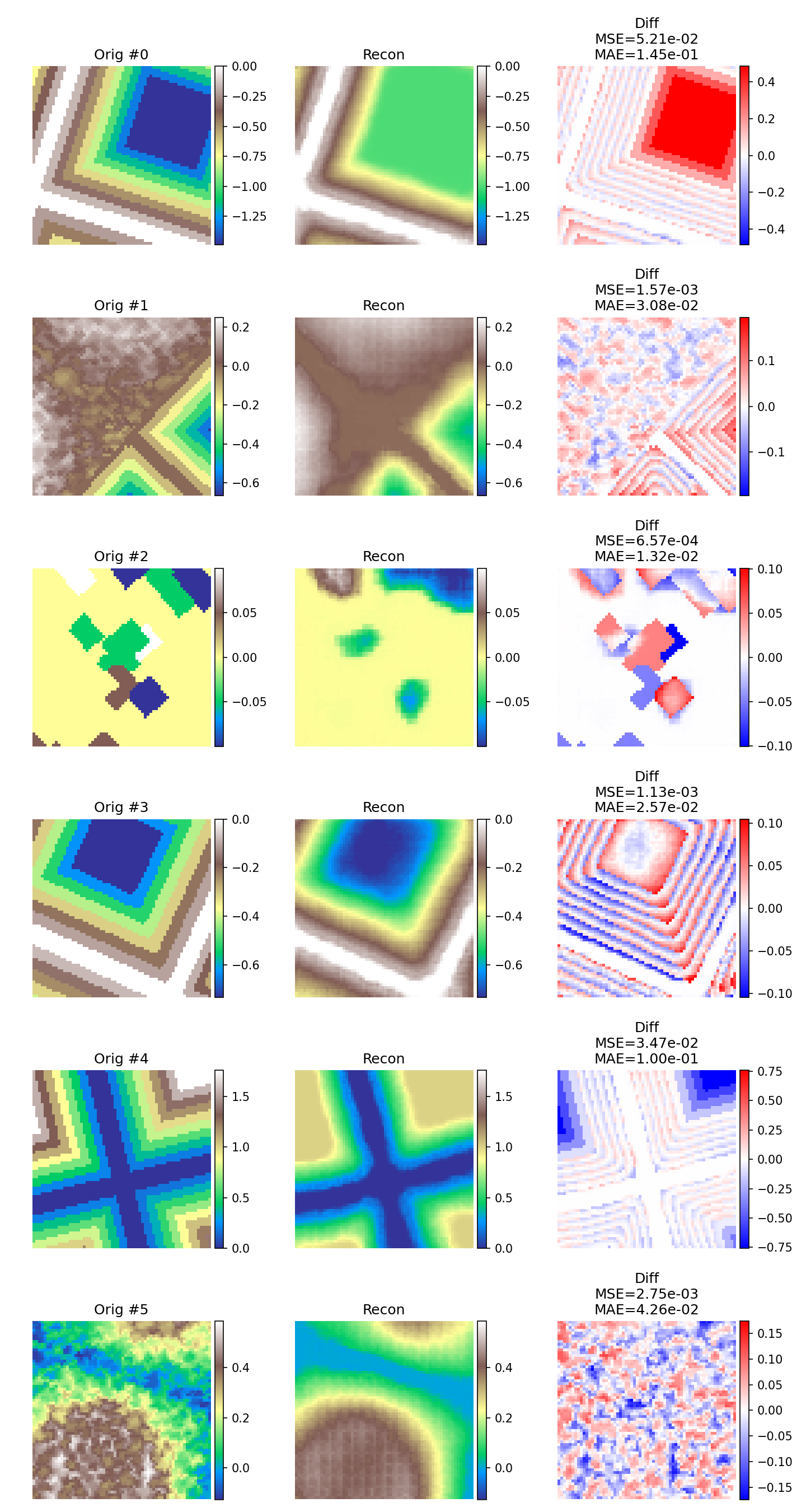
如图所示,模型在重构中能够较好地捕捉大尺度结构,尤其是高程分布和主要形状,但在细节还原上表现不足,高频纹理和锐利边缘往往被平滑化,这是卷积自编码器常见的问题。SWD 正则化在一定程度上促使潜在空间分布更加光滑,从而提升整体结构一致性,但也可能牺牲部分精细还原能力。对于噪声较多的样本(如 #1、#5),模型更倾向于生成较为“干净”的版本,而非精确还原原始纹理。
参考材料
-
逐际动力开源运控 tron1-rl-isaacgym:https://github.com/limxdynamics/tron1-rl-isaacgym
-
Advanced skills by learning locomotion and local navigation end-to-end (iros 2022)
-
Terrain-attentive learning for efficient 6-DoF kinodynamic modeling on vertically challenging terrain (iros 2024)
