笔试——Day35

第一题

题目

奇数位丢弃

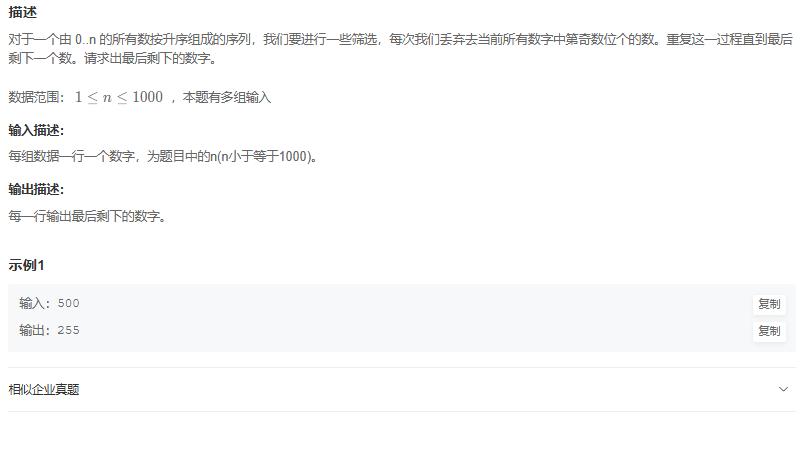
思路

找规律

0, 1, 2, 3, 4, 5, 6, 7, 8, 9
1, 3, 5, 7, 9
3, 7
7
显然，每次第一个删除的数字为2 ^ n - 1，所以我们需要找到小于n最大的2^n的数，再减一就是结果

代码

#include <iostream>
#include <cmath>
using namespace std;int main() 
{int n;while(cin >> n){int res = 1;while(res <= n){res *= 2;}cout << res / 2 - 1 << endl;}return 0;
}
// 64 位输出请用 printf("%lld")

第二题

题目：

求和

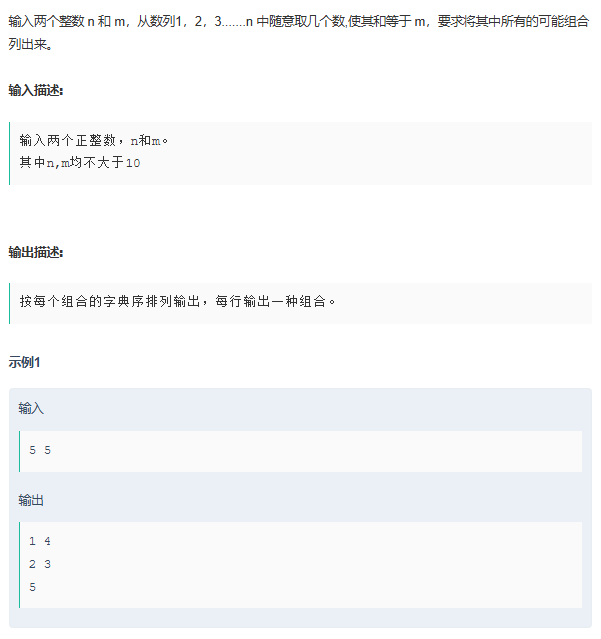
思路

DFS

代码

#include <iostream>
using namespace std;bool visited[11] = {0};
int sum = 0; // 路径和
int n, m; void dfs(int pos)
{if(sum == m){for(int i = 1; i <= n; i++){if(visited[i]) cout << i << " "; }cout << endl;return ;}if(sum > m || pos > n) return ;// 选 possum += pos;visited[pos] = true;dfs(pos + 1);sum -= pos;visited[pos] = false;// 不选 posdfs(pos + 1);}
int main() 
{cin >> n >> m;dfs(1);return 0;
}
// 64 位输出请用 printf("%lld")

第三题

题目：

计算字符串的编辑距离

思路

动态规划

• 状态表示：
  dp[i][j]表示：字符串a中[1, i]以及字符串b中[1, j]区间内的编辑距离；

• 状态转移方程：
  a[i] == b[j]->dp[i - 1][j - 1]
a[i] != b[j]->

  • 删除：dp[i - 1][j] + 1
  • 增加：dp[i][j - 1] + 1
  • 替换：dp[i - 1][j - 1] + 1

• 返回值：
  dp[n][m]

代码

// https://www.nowcoder.com/practice/3959837097c7413a961a135d7104c314?tpId=37&tqId=21275&ru=/exam/oj
#include <iostream>
#include <string>
using namespace std;
const int N = 1010;
string a, b;
int dp[N][N];
int main()
{cin >> a >> b;int n = a.size(), m = b.size();for (int j = 0; j <= m; j++)dp[0][j] = j;for (int i = 0; i <= n; i++)dp[i][0] = i;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){if (a[i - 1] == b[j - 1])dp[i][j] = dp[i - 1][j - 1];elsedp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) +1;}}cout << dp[n][m] << endl;return 0;
}