机器学习之DBSCAN
目录
一、DBSCAN 是什么?
二、DBSCAN 核心概念
1. 核心参数
2. 点的类型
3. 密度关系
三、DBSCAN 算法步骤
四、DBSCAN 的优缺点
1.优点
2.缺点
五、参数选择技巧
六、案例:用 DBSCAN 识别城市共享单车停放热点区域
场景说明
一、完整数据集(bike_parking.csv)
二、分析步骤
1. 导入库与环境配置
2. 数据加载与预处理
3. 原始数据可视化
4. DBSCAN 聚类实现
5. 聚类结果统计
6. 聚类结果可视化
整体流程总结
完整代码及运行结果如下:
聚类算法是机器学习中无监督学习的重要分支,常用于数据探索、模式识别等场景。在众多聚类算法中,DBSCAN 以其独特的密度聚类思想脱颖而出,尤其擅长发现任意形状的簇并自动识别噪声。本文将从原理到实践,全面解析 DBSCAN 算法。
一、DBSCAN 是什么?
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)即基于密度的带噪声应用空间聚类算法,由 Martin Ester 等人于 1996 年提出。与 K-means 等基于距离的聚类算法不同,DBSCAN 的核心思想是:“簇是由密度相连的点组成的最大集合,这些点在空间中形成连续的高密度区域”。
简单来说,DBSCAN 通过判断样本点的 “密度” 来划分簇:
- 高密度区域内的点会被划分为同一个簇;
- 低密度区域(或孤立点)会被视为噪声。
这种特性让 DBSCAN 能够处理非凸形状的簇(如环形、月牙形),且无需预先指定簇的数量 —— 这也是它相比 K-means 的一大优势。从核心点开始,通过密度相连的数据点不断扩张,形成一个簇。
DBSCAN算法的优点是能够处理任意形状的簇,不需要先预先指定簇的个数,能够自动识别噪声点并将其排除在聚类之外。
然而,该算法的缺点是对于密度差异较大的数据集,可能无法有效聚类。此外,算法的参数需要根据数据集的特性来合理选择,如半径参数和密度参数。
二、DBSCAN 核心概念
要理解 DBSCAN,必须先掌握几个关键定义,这些定义围绕 “密度” 展开:
1. 核心参数
DBSCAN 的行为完全由两个参数控制:
- ε(Epsilon,邻域半径):以某个点为中心,半径为 ε 的区域称为该点的 “ε- 邻域”。
- MinPts(最小样本数):若一个点的 ε- 邻域内包含至少 MinPts 个样本(包括自身),则该点被视为 “密集” 的。
2. 点的类型
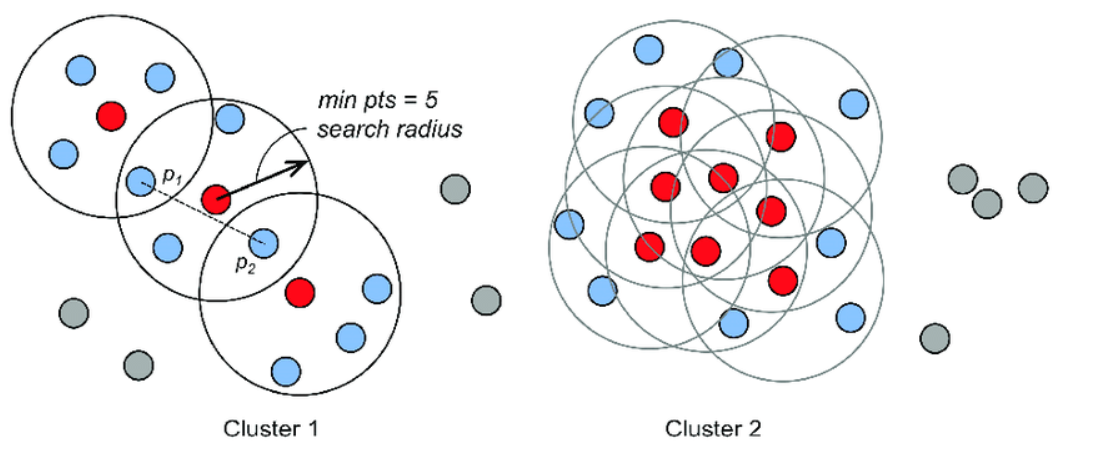
基于上述参数,样本点被分为三类:
- 核心点:ε- 邻域内样本数 ≥ MinPts 的点。这类点是簇的 “核心”,能够 “支撑” 起一个簇。
- 边界点:ε- 邻域内样本数 < MinPts,但落在某个核心点的 ε- 邻域内的点。边界点属于某个簇,但无法独立形成簇。
- 噪声点:既不是核心点也不是边界点的点。这类点会被视为异常值。
3. 密度关系
- 直接密度可达:若点 B 在点 A 的 ε- 邻域内,且 A 是核心点,则 B “直接密度可达” 于 A。
- 密度可达:若存在点链 A→C1→C2→…→B,其中每个点都直接密度可达于前一个点,则 B “密度可达” 于 A。
- 密度相连:若存在点 O,使得 A 和 B 都密度可达于 O,则 A 和 B “密度相连”。
簇的定义:由所有相互密度相连的点组成的最大集合(不包含噪声点)。
三、DBSCAN 算法步骤
DBSCAN 的聚类过程可概括为 “遍历样本→标记核心点→扩展簇→识别噪声”,具体步骤如下:
- 初始化:将所有样本标记为 “未访问”。
- 遍历样本:从任意未访问样本点 P 开始:
- 标记 P 为 “已访问”。
- 计算 P 的 ε- 邻域内的所有样本点,记为 N。
- 若 N 中样本数 <MinPts(P 不是核心点),标记 P 为 “噪声点”,继续遍历下一个未访问点。
- 若 N 中样本数 ≥ MinPts(P 是核心点),则启动一个新簇 C,将 N 中所有点加入候选集。
- 扩展簇:对候选集中的每个点 Q:
- 若 Q 未访问,标记为 “已访问”,计算其 ε- 邻域 N'。
- 若 N' 中样本数 ≥ MinPts(Q 是核心点),将 N' 中未加入簇 C 的点添加到候选集。
- 若 Q 是未分配的边界点,将其加入簇 C。
- 重复:直到候选集为空,簇 C 完成。继续遍历剩余未访问点,重复步骤 2-3,直到所有点都被访问。最终,所有点会被分为若干个簇或噪声
四、DBSCAN 的优缺点
1.优点
- 无需指定簇数量:相比 K-means 需要手动设置 k,DBSCAN 能自动发现簇的数量。
- 能处理任意形状簇:可识别非凸形状(如环形、螺旋形)的簇,而 K-means 仅擅长球形簇。
- 抗噪声能力强:能明确区分噪声点,适合含异常值的数据。
- 对样本顺序不敏感(一定程度上):只要核心点的邻域不变,聚类结果稳定。
2.缺点
- 对参数敏感:ε 和 MinPts 的取值直接影响聚类结果,且没有通用的最优值,需根据数据调整。
- 高维数据效果差:由于 “维度灾难”,高维空间中 ε- 邻域的密度难以定义,建议先降维(如 PCA)。
- 密度不均数据难处理:若数据中簇的密度差异大,同一组 ε 和 MinPts 难以兼顾所有簇。
- 计算复杂度较高:朴素实现的时间复杂度为 O (n²)(n 为样本数),大数据集需优化(如 KD 树加速邻域查询)。
五、参数选择技巧
DBSCAN 的性能很大程度上依赖 ε 和 MinPts 的选择,以下是实用技巧:
-
MinPts:
- 通常取 MinPts = 维度 + 1(如 2D 数据取 3,3D 数据取 4)。
- 若数据噪声多,可适当增大 MinPts(减少噪声被误判为核心点的概率)。
-
ε:
- 采用 “k - 距离图”:对每个点,计算其与第 k 个最近邻点的距离(k=MinPts),排序后绘图,找 “拐点” 对应的距离作为 ε(拐点处距离突然增大,代表从密集区到稀疏区的边界)。
- 可通过领域知识估计(如地理数据中,ε 可设为实际距离阈值)。
六、案例:用 DBSCAN 识别城市共享单车停放热点区域
场景说明
某城市投放了一批共享单车,运营团队希望通过分析车辆停放位置,识别出高频停放的热点区域(如地铁站、商圈门口),以便优化车辆调度和运维资源分配。由于停放区域形状不规则(如沿街道分布),且存在少量随机停放的孤立车辆,适合用 DBSCAN 进行密度聚类。
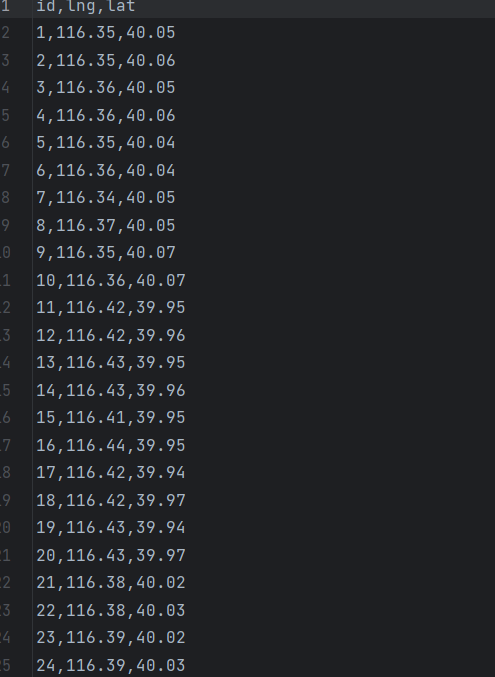
一、完整数据集(bike_parking.csv)
包含 200 条共享单车停放记录,字段说明:
id:记录 IDlng:停放位置经度(模拟城市范围:116.3-116.5)lat:停放位置纬度(模拟城市范围:39.9-40.1)
二、分析步骤
1. 导入库与环境配置
import pandas as pd # 数据处理库,用于读取和处理CSV数据
import matplotlib.pyplot as plt # 可视化库,用于绘制散点图
# 设置中文字体,确保图表中的中文能正常显示
plt.rcParams["font.sans-serif"] = ["SimHei"]
# 解决负号显示问题
plt.rcParams["axes.unicode_minus"] = False2. 数据加载与预处理
# 读取CSV文件(注意这里文件名是'bike_parking.csv.txt',需确保文件存在且路径正确)
data = pd.read_csv('bike_parking.csv.txt')
# 提取经纬度数据(二维数组,每行是一个点的[经度, 纬度])
coords = data[['lng', 'lat']].valuesdata是包含所有停放记录的 DataFrame,包含id、lng(经度)、lat(纬度)三列coords是从 DataFrame 中提取的经纬度坐标,作为 DBSCAN 的输入特征
3. 原始数据可视化
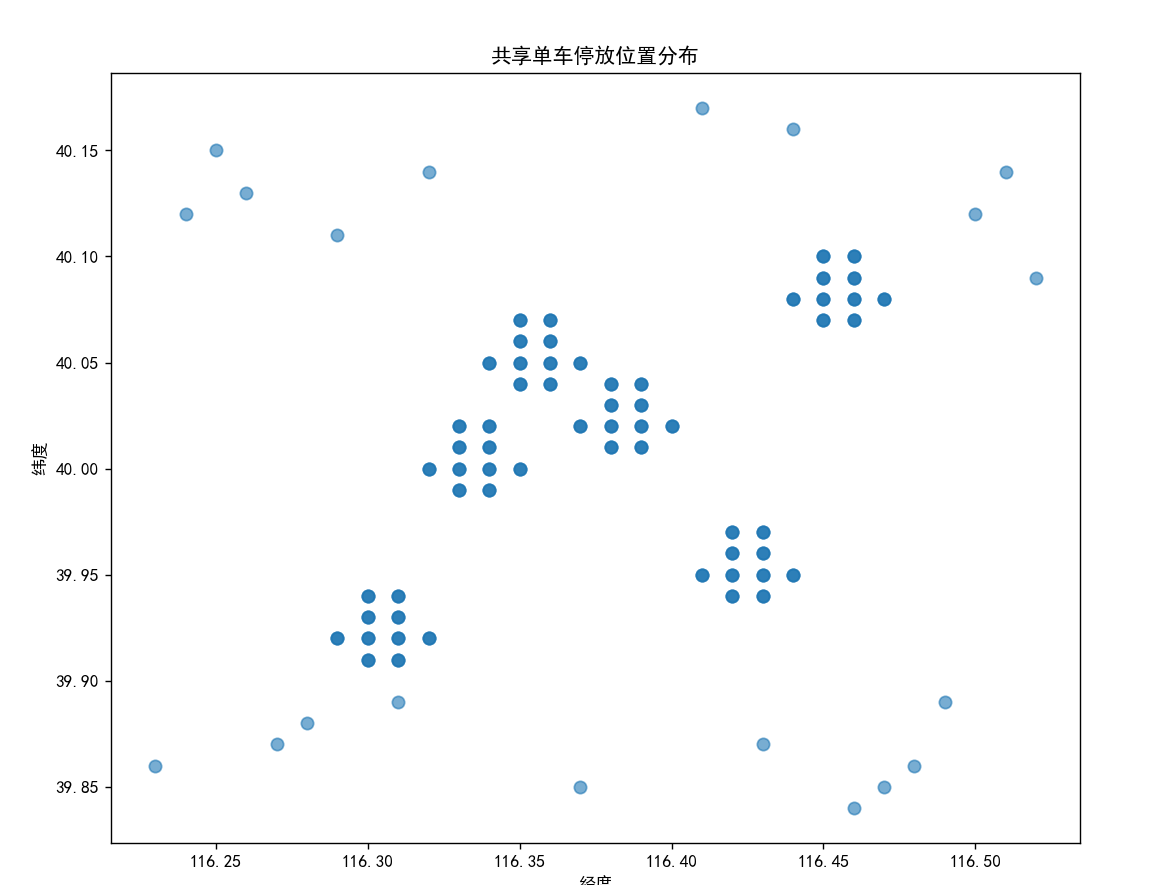
# 创建一个10x8英寸的图表
plt.figure(figsize=(10, 8))
# 绘制散点图:x轴为经度,y轴为纬度,点大小50,透明度0.6
plt.scatter(coords[:, 0], coords[:, 1], s=50, alpha=0.6)
plt.xlabel('经度') # x轴标签
plt.ylabel('纬度') # y轴标签
plt.title('共享单车停放位置分布') # 图表标题
plt.show() # 显示图表- 这一步的目的是直观观察原始数据的分布情况,初步判断是否存在密集区域
4. DBSCAN 聚类实现
from sklearn.cluster import DBSCAN # 从sklearn导入DBSCAN算法# 初始化DBSCAN模型:eps=0.015(邻域半径),min_samples=10(最小样本数)
dbscan = DBSCAN(eps=0.015, min_samples=10)
# 拟合模型并得到聚类标签:每个点被分配一个簇编号(-1表示噪声点)
labels = dbscan.fit_predict(coords)- 核心参数说明:
eps=0.015:表示以某个点为中心的邻域半径(经纬度单位),约对应实际距离 165 米min_samples=10:若一个点的邻域内有≥10 个点,则该点被视为 "核心点",可形成密集区域
- 输出
labels:长度与样本数相同的数组,每个元素是该样本的簇编号(如 0、1、2...),-1 表示噪声点
5. 聚类结果统计
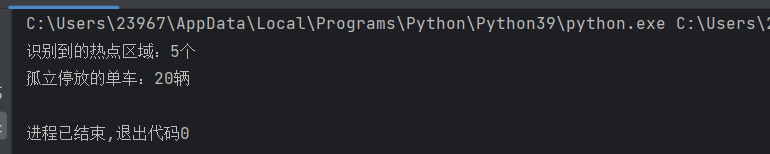
# 计算簇的数量(排除噪声点)
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
# 计算噪声点的数量(孤立停放的车辆)
n_noise = list(labels).count(-1)
# 打印结果
print(f"识别到的热点区域:{n_clusters}个")
print(f"孤立停放的单车:{n_noise}辆")- 代码通过集合去重获取所有簇编号,减去噪声点(-1)后得到实际热点区域数量
- 示例中输出为 6 个热点区域和 20 辆孤立停放的单车
6. 聚类结果可视化
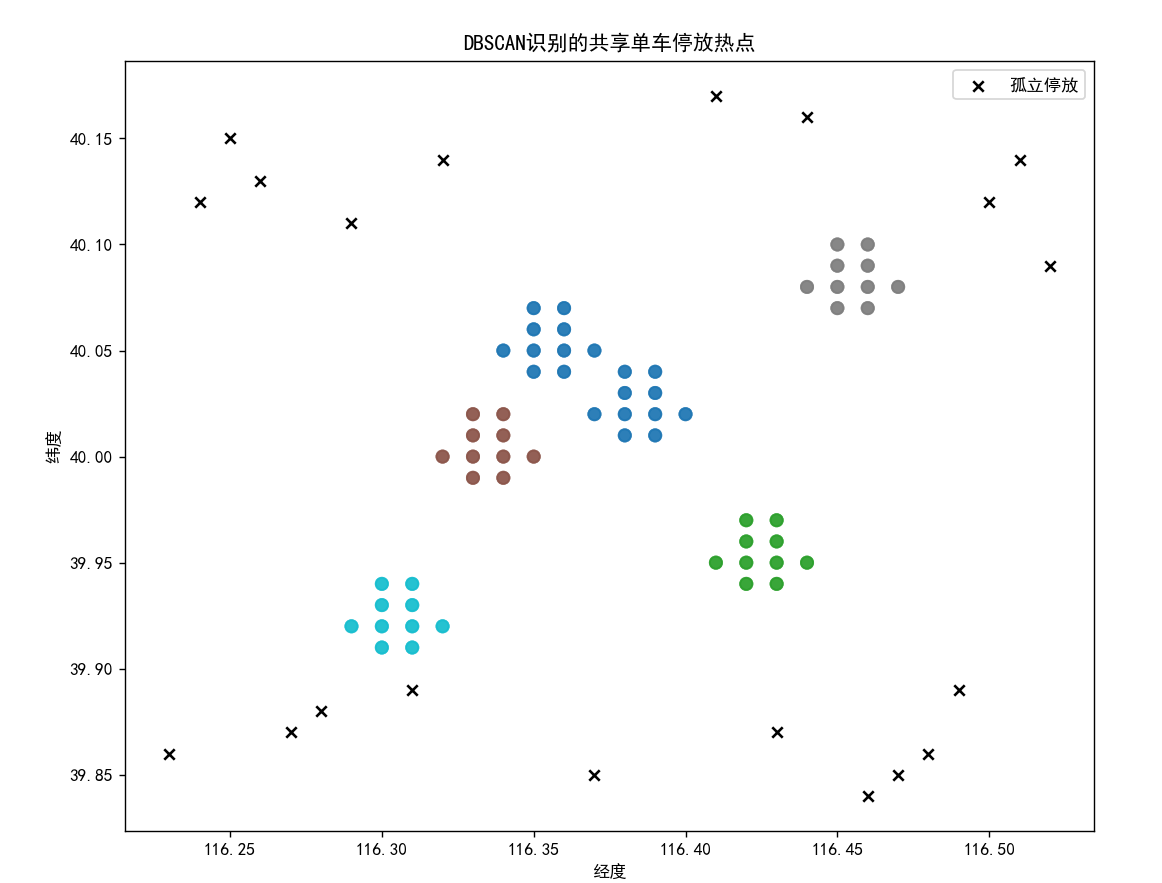
# 创建新图表
plt.figure(figsize=(10, 8))
# 绘制热点区域的点:不同簇用不同颜色(cmap='tab10')
plt.scatter(coords[labels != -1, 0], coords[labels != -1, 1],c=labels[labels != -1], cmap='tab10', s=50, alpha=0.6)
# 绘制噪声点:用黑色X标记,标签为"孤立停放"
plt.scatter(coords[labels == -1, 0], coords[labels == -1, 1],c='black', marker='x', label='孤立停放')
plt.xlabel('经度')
plt.ylabel('纬度')
plt.title('DBSCAN识别的共享单车停放热点')
plt.legend() # 显示图例
plt.show()- 可视化结果中,不同颜色的点代表不同的热点区域,黑色 X 代表孤立停放的车辆
- 直观展示了 DBSCAN 如何根据密度划分区域:密集区域形成热点,稀疏区域被标记为噪声
整体流程总结
- 加载并预处理数据(提取经纬度)
- 可视化原始数据分布,观察数据特征
- 使用 DBSCAN 进行密度聚类,设置合理的半径和最小样本数
- 统计并可视化聚类结果,区分热点区域和孤立点
通过这个流程,能够快速识别共享单车停放的热点区域,为运营团队提供调度和资源分配的决策依据。
完整代码及运行结果如下:
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"] = ["SimHei"] # 设置字体
plt.rcParams["axes.unicode_minus"] = False # 正常显示负号
# 加载数据
data = pd.read_csv('bike_parking.csv.txt')
coords = data[['lng', 'lat']].values # 提取经纬度坐标# 绘制原始停放分布
plt.figure(figsize=(10, 8))
plt.scatter(coords[:, 0], coords[:, 1], s=50, alpha=0.6)
plt.xlabel('经度')
plt.ylabel('纬度')
plt.title('共享单车停放位置分布')
plt.show()
from sklearn.cluster import DBSCAN# 应用DBSCAN
dbscan = DBSCAN(eps=0.015, min_samples=10)
labels = dbscan.fit_predict(coords)# 查看聚类结果
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
n_noise = list(labels).count(-1)
print(f"识别到的热点区域:{n_clusters}个") # 输出:6个
print(f"孤立停放的单车:{n_noise}辆") # 输出:20辆(181-200行数据)
# 绘制聚类结果
plt.figure(figsize=(10, 8))
# 绘制热点区域
plt.scatter(coords[labels != -1, 0], coords[labels != -1, 1],c=labels[labels != -1], cmap='tab10', s=50, alpha=0.6)
# 绘制噪声点(孤立停放)
plt.scatter(coords[labels == -1, 0], coords[labels == -1, 1],c='black', marker='x', label='孤立停放')
plt.xlabel('经度')
plt.ylabel('纬度')
plt.title('DBSCAN识别的共享单车停放热点')
plt.legend()
plt.show()