当前位置：首页 > news >正文

算法讲解--水果成篮

news 2025/8/13 9:47:44

一，题目描述

该题目的要求是得出水果的最大数目。有几个限制条件：

1，只有两个篮子，并且每种篮子只能装一种水果。

2，单个篮子对数量没有上线。

3，一棵树只能摘一个水果。

4，当这棵树摘完之后，必须右移下一颗树。

而此已知的条件有：

1，可以选择任何一棵树开始，但是一旦开始就必须连续，直到摘到因为不符合条件停止采摘。

2，知道每棵树的种类，以及总数。

因此这个题的本质就就是如何选择可以得出最长满足要求的子数组问题。而这里的满足要求就是，这个子数组的种类不超过两种的情况下尽可能的多。

如示例一：

一共有三棵树，但是只有两种类型所以都可以装下。

如示例二：

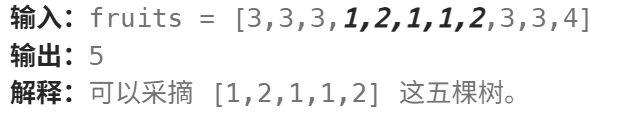
一共有四种类型，一共十一棵树，但是因为只能有两个篮子，所以只能装两种类型的水果，若从头开始（3，3，3，1）则这是一种摘法；（1，2，1，1，2）这是一种摘法；（3，3，4）这也是一种摘法。这这些摘法会发现，要保证连续并且种类小于等于2。

二，算法讲解

在上述的讲解中，大概了解了题目的意思。将题目转化成算法题等价与：给一个数组在这个数组中选取最长的连续子数组（该子数组只能有两种元素）。

1，暴力枚举

通过遍历数组，遍历出所有的数组可能性。判断每一种可能性是否满足题目中的要求。以示例二为例。通过left，right两个指针进行控制如图：

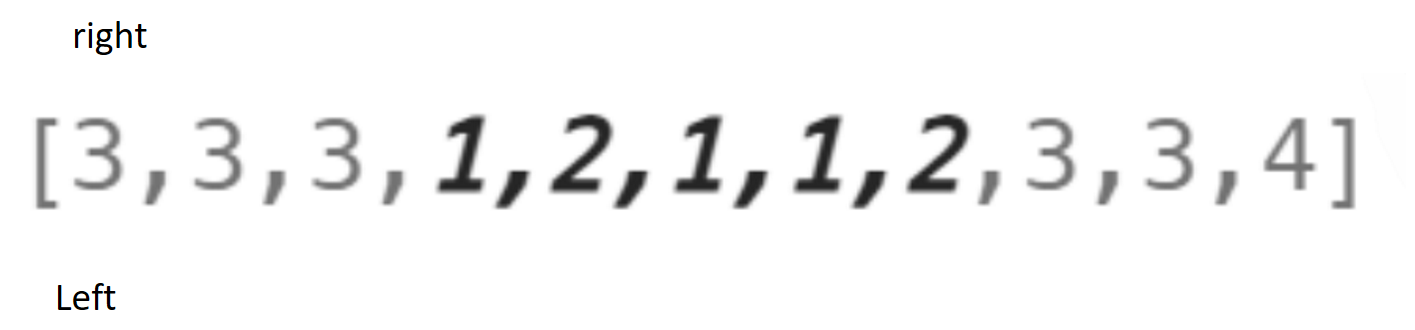
这是left和right的起始位置。之后right不断的加加，判断left到right所围成的区域的子数组是否满足题意。如图：

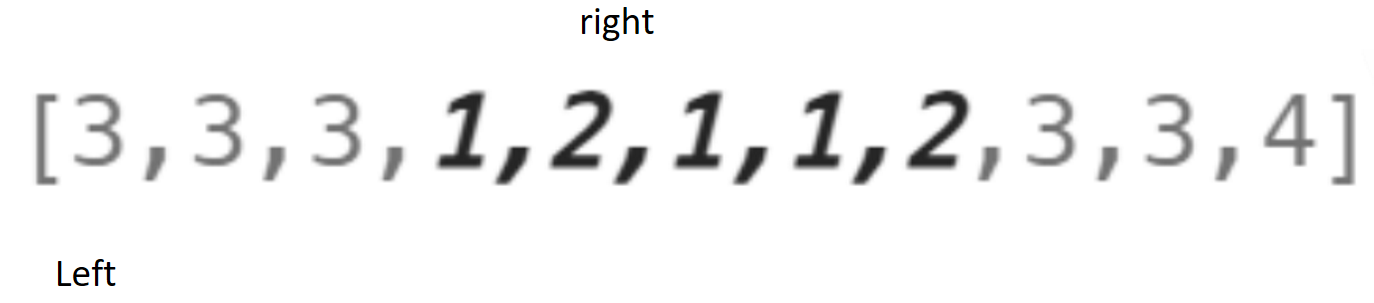
此时的right处于临界位置，当right之前的位置都满足，而之后的就不满足。直到right结束如图：

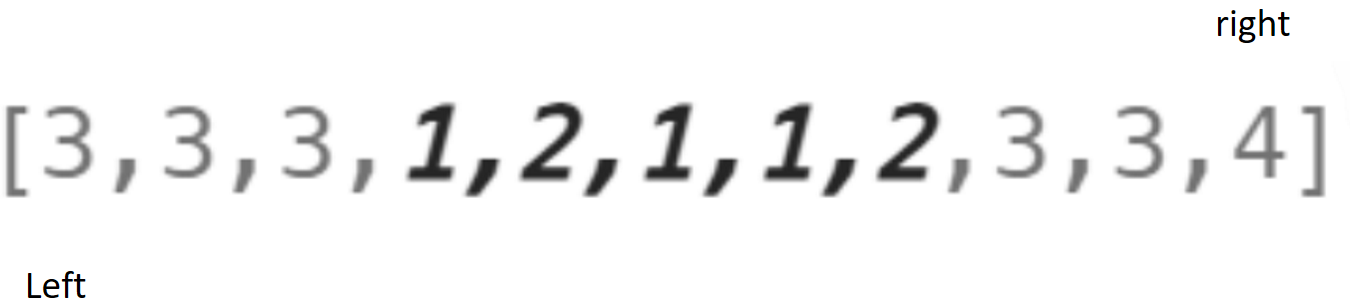
此时第一组，遍历结束，left++，left = right。如图：

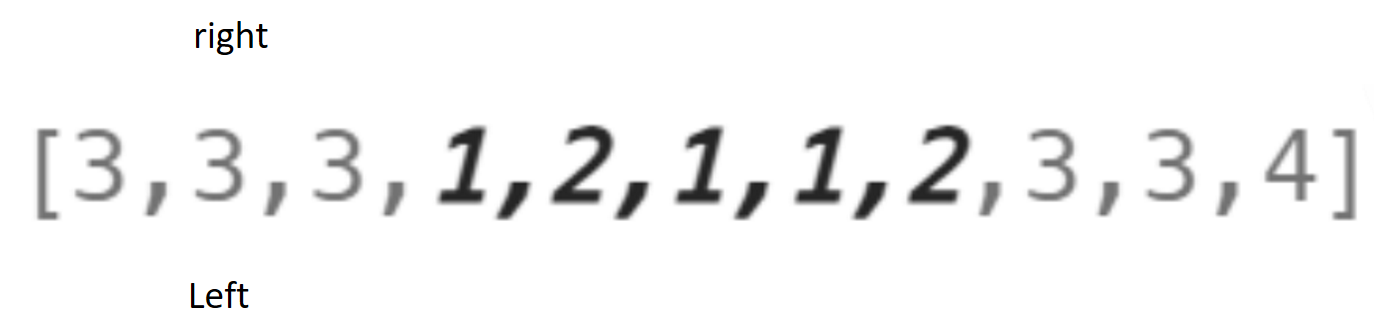
重复第一组的过程直到left结束，整个数组遍历结束，选取最大的子数组并且进行返回。

在上述这个过程会发现，left和right遍历了许多不需要遍历的情况，如当right到临界条件之后，不在需要继续遍历。而left++之后，right也不必要会到和left相同的位置进行重新遍历。因此引出了第二种方法

2，滑动窗口法

在暴力枚举的基础上进行改造。起始和暴力枚举相同设置的left和right指针和上图一致。之后判断是否满足临界条件，只要不满足right就++如图：

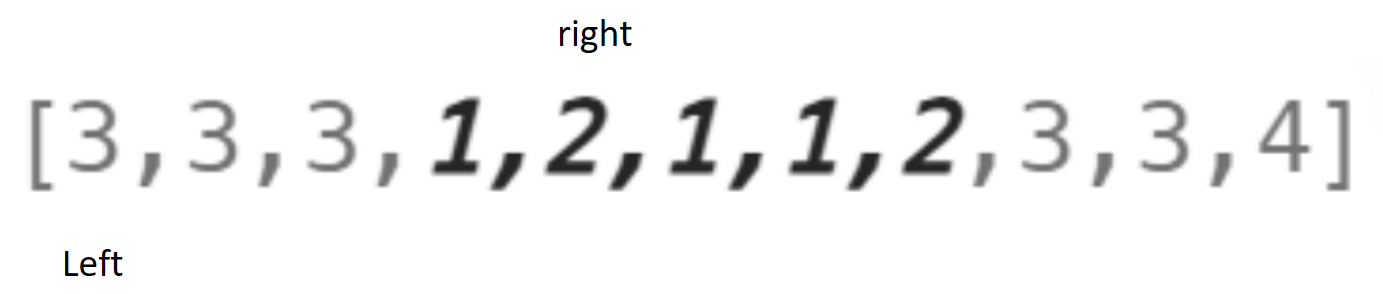
此时若right再向右就超出两种类型，就超出两种类型，如图：

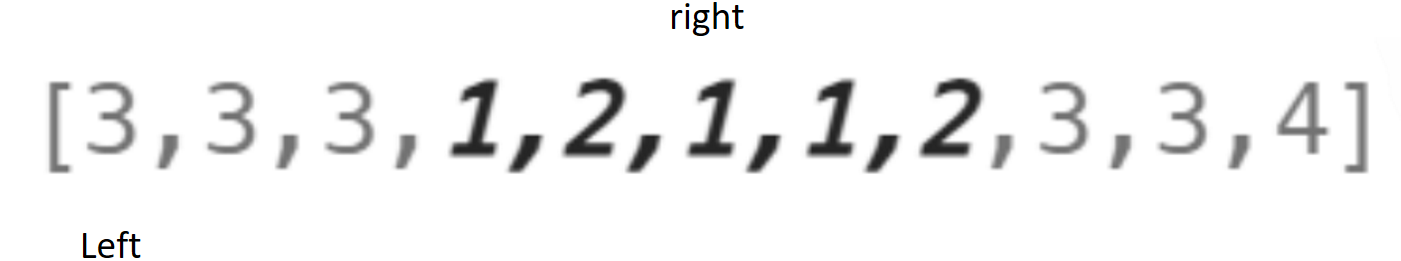
此时子数组共有三种类型，left++，判断时候满足题目中的两种类型，不满足继续left++，直到满足条件如图：

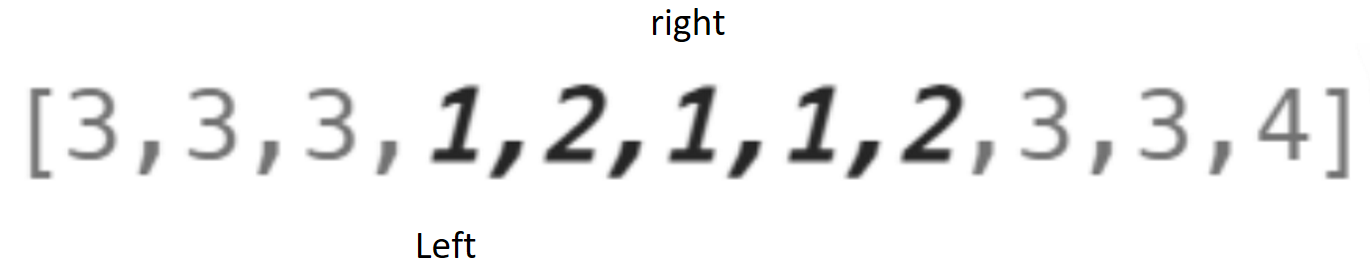
重复上述步骤，直到right遍历完整个数组。该算法结束。每次满足条件的时候记录子数组长度返回最大子数组的长度。

3，记录讲解

在上述移动过程中会发现，不仅要记录数据的个数比如说3出现的次数，1出现的次数，还有记录出现的类型，比如1，3这些有没有出现，以便于left进行++，可以给好的删除数据，本质上来说，left的++，是要删除一种类型，因此，right每一次++，都要记录该子数组的类型，和各类型所站的个数为多少。

这是需要借助一个数据结构map这个容器进行存储，right的每一次++，都将该数据存储在map容器中，left++，就减去这个容器中对应的数据。map.size()可以判断该子数组中有多少种类型的数据。根据此来判断是否满足right的临界条件。

三，代码示例

 int totalFruit(vector<int>& fruits) {map<int,int> s;int left = 0;int right = 0;int number = 0;while(right < fruits.size()){s[fruits[right]]++;right++;while(s.size() >= 3){s[fruits[left]]--;if(s[fruits[left]] == 0){s.erase(fruits[left]);}left++;}number = max(number, (right - left));}return number;}

number记录有效的子数组长度；当map容器一种类型的数据减到零，则删除这种类型的数据。以此控制子数组的类型数量。最终返回最长的子数组的个数。