当前位置：首页 > news >正文

special topic 8 (2) and topic 9 (1)

news 2025/8/11 14:58:23

前言

从今天开始，再也不考虑进度，不考虑任何其他问题，只考虑具体的知识点。慢慢来，也不给自己毒鸡汤了，就是慢慢来。笔记也不要着急，看一节网课，把对应的练习题，例题，知识点，整理完了一遍之后上传一次笔记，这样不会心浮气躁，很棒。

148

这题还是比较难的。给出邻域，我们考虑包括这个点，去心邻域的话，就是不包括这个点，包括这个点，邻域内满足的条件，我们可以直接把这个点代入得到一个不等式，从而得到一个结果。然后对不等式两边求极限，夹逼准则可以得到中间的式子的绝对值的极限是零，实际上我单独考知道一个绝对值的极限是零可以推这个极限就是零，要推导也很简单，就是用 $ϵ−δ\epsilon-\delta$ 来描述极限，刚好这里直接复习一下。 $∀ϵ>0,∃δ>0,0<∣x−x0∣<δ,s.t.∣f(x)−A∣<δ⇔lim⁡x→x0f(x)=A\forall \epsilon>0,\exist\delta>0,0<|x-x_0|<\delta,s.t.|f(x)-A|<\delta\Leftrightarrow\lim\limits_{x\to x_0}f(x)=A$

然后就可以推导出来这个结论了。然后就是用夹逼准则，实际上也没难度。还有一个方法，可以用特殊函数来排除，比如说让函数恒为零，满足题目的条件，然后排除掉三个选项，最后选出正确答案。建立这种做题直觉是好的。

149

这题的话，没啥操作性，可能就是复合函数求导的时候慢一点，谨慎一点。除了常规的方法，还有一个比较巧妙的方法，就是，我们观察到函数是一堆式子的乘积，可以让前面是一个函数，后面是一个函数，对原来函数求导，可以转换为函数的乘法求导，因为有一部分求导之前是一个零，所以可以消掉，可以极大地降低计算量。好方法！

150

这题是极限不存在，我第一次遇到算导数，然后最后写一个导数不存在的情况的。太秀了。左右开弓，指数，反正切，绝对值，取整，分段。左右开弓五种情况。倒计时 132 天了。加油啊。

154

这题就是考察一个结论，就是一个函数写成 $f(x)=g(x)|x-x_0|$ , 然后在 g(x) = 0 的时候这个函数在 $x=x_0$ 处是可导的，相当于让零把函数尖锐的角磨平了，让曲线上那点变得光滑，光滑就意味着可导。

还有两个结论，懒得敲了，直接拍照得了。

在这里插入图片描述

想起来看到过的一句话，说，如果一道题只做一遍，没有吃透是没有任何意义的，笔记如果做了之后不反复复习也是没有意义的。我感觉很有道理，虽然我不喜欢看自己写的笔记。但是自己做的笔记，肯定还是记到脑子里面了一部分的，退而求其次，尽量把做过的数学题多做几遍，尽力吃透，看完强化课就不看网课了吧，感觉基本知识点都学会了，后面就是要不断地做题和总结了。

157

这题是两种方法，一种是洛必达，一种是泰勒。洛必达注意是洛到连续的那一阶，至多洛到连续的那一阶，一般也是洛到连续的那一阶。把 $x_0$ 看成常数。泰勒注意皮亚诺余项的泰勒展开的标准形式。皮亚诺 Peano, 泰勒 Taylor

这题还有一个非常好用的公式。 $lim⁡x→0f(x0+ax)−f(x0+bx)x=(a−b)f′(x)\lim\limits_{x\to 0}\frac{f(x_0+ax)-f(x_0+bx)}{x}=(a-b)f'(x)$ ,前提是这个函数一阶可导。然后这题就能快速解决了。从这节课开始，所有对应的例题，练习题，知识点都要吃透。吃得透透的。

强化 58

这题有两种方法，然后求微分方程也有两种方法。感觉长时间用眼对眼睛不好，难以长时间作战，所以的话，学习半个小时，一个小时就休息一下，身体是自己的，要对自己负责任。。。套公式比分离变量要快一点。对两边求极限，假设把 $Δx\Delta x$ 视为变量，那么 x 和 f(x) 都是常数，这块我稍微有点不熟练。等强化结束，就是一个人慢慢做题，不会的就问别人，搞清楚，然后提升自己的做题水平。

强化 59

首先是，对数函数的真数假设是根式，把根式写成幂指数，然后提到前面作为对数函数的系数。这题有一个方法就是慢慢把函数完整地写出来，画图数形结合，分类讨论，然后算出来，非常考察细致和耐心。

还有一个方法，就是用复合函数求导法则，把自变量代进去，把中间变量算出来。也很简单，比第一种方法更加不容易出错。以后我一道题，有一种解题方法，就标记一颗星。

2.18

隐函数求导，就是对方程两边同时求导，一般变态一点求导到二阶就差不多了，最好用 f’(x)、f’'(x) 这种形式，不容易弄混，函数，一阶导数，二阶导数，每个方程都把对应的函数值写出来，最后代进去做计算就可以得到答案。很简单的一道题。午睡半小时去。嘿嘿。

强化 60

隐函数求导，虽然说就是对两边同时求导，但是还是可以包装一下的。比如说，我们给一个隐函数，然后让我们求一个极限，就和变限函数一样，看到变限函数，就忍不住想要求导，看到隐函数，就忍不住想要求导。

这块看到 $1x\frac1x$ 可以考虑倒代换，然后出现了 $lim⁡t→0+f(t)−f(2t)t\lim\limits_{t\to 0^+}\frac{f(t)-f(2t)}t$ ，看到这个形式，t 是动点，双动点作差的问题，忍不住考虑导数是否存在，实际上一般的隐函数的 y ，一阶导数，二阶导数，高阶导数都是存在的。可以用导数定义，这块为了加快解题速度，可以直接上结论，就是 $lim⁡x→0f(x0+ax)−f(x0+bx)x=(a−b)f′(x0)\lim\limits_{x\to0}\frac{f(x_0+ax)-f(x_0+bx)}{x}=(a-b)f'(x_0)$ ，应该就可以了。然后算隐函数导数没什么好说的，奥，特殊点一般能消掉，所以的话，计算不一定要算到底，虽然算到底计算量也不大。所以只是提一嘴。

还有一个方法就是导数存在，二阶导数存在，那么一阶导数连续，那么可以求导到一阶导数这一阶，也就是说原来的式子可以用洛必达，然后也可以算出来，最后算一个导数，取个相反数就是答案。

159

这题计算量还挺大，我算错了。这里是要用到对数运算的技巧。真数相乘就拆开变成加法，真数相除拆开变成减法。指数提到前面变成系数。就一个正常求导我就倒下了，绷不住啊。

160

这题就是算一个极限，然后简单的求导，我还是得自己给自己一些正反馈。自己给自己加油打气哈哈哈。

161

这题就是简单的复合函数求导，实际上是基础板块的题，强化阶段写一下基础阶段的题，没啥问题。回头看的力量。就是我们现在去看，基础阶段的题，到底是感觉还是那么困难，还是已经很轻松了。这是个问题，这是一场漫长的战斗，确实可以多多休息。但不是放松。

162

隐函数求导，给一个方程，对方程两边，求一阶导数，求二阶导数，然后代值做计算，求二阶导数就是在一阶导数的基础上，两边同时再导一次，感觉可以出一个五分的填空题吧，也算是有一定的计算量呢。

163

这题难度很大，我考虑了两种解法，算出来的答案差了四倍，不知道哪个是对的，或者不知道是哪里出了问题。算出来的答案是一致的，但是我考虑的一个点就是，y 是否二阶可导呢。我不知道怎么判断。实际上只要判断一个点处的二阶导数是否存在就可以了，一个点处的二阶导数很容易判断出来。群友水平很高。很厉害。

还有一个方法，就是，对两边同时除以 x,不把这个看成是隐函数，看成是一个等价无穷小问题。两边对趋近于零的时候取极限，然后算出来一个比值，换元之后就可以得到最后的答案了。

164

这题我硬算，算了两遍，答案都不对哇。要取对数，然后拆开就很容易算了。我还以为是用有理函数拆开，还以为自己是个小天才呢。取对数之后没任何难度了。

165

todo

强化 61

听了一遍之后还是差点翻车了。因为代值的时候有点不够谨慎。这题的话，难度不大，别把 f(x) and y 搞混了就可以了。卡住我的点在于，我没意识到，不知道 f’'(0) 也可以算这个题。因为二阶导数的系数，因为题目设置的原因，肯定就是零。还有一个细节就是求导没必要求到最后面，出现乘积为零的式子的时候（代值进去结果是零）就可以表示一下，意思一下，别使劲去算了就，第一容易算错，第二浪费时间。爽。

151

刚学了一个导数极限定理，想要做一下这个题，好像做不了，老老实实用导数定义算了一遍。导数极限定理的意思是，函数在去心邻域内可导，该点连续，导数在该点的极限不振荡，那么该点的导数，等于导数在该点去心邻域的极限。感觉自己傻了。东一下，西一下，不合适。老老实实先把这个课程的例题做完才是王道。别总是跳来跳去的。

强化 62

今天一定要把这节强化课听完，听完之后就去学一下专业课。数学和专业课是大头，休息也是非常重要。不然学一段时间之后，眼睛废了，或者颈椎废了，或者腰椎废了，得不偿失啊。这题是导数极限定理的证明，假设函数的导数在某点的邻域内的极限是不振荡的，函数在这个点是连续的，并且去心邻域内是可导的，那么，可以把导数按照导数定义展开，满足零比零，分子分母去心邻域内都可导，最后的结果不振荡，所以可以用洛必达，所以得到了，某点导数等于，导数在这个去心邻域的极限值。证毕。

感觉自己学习可以学习三天新的知识，复习一天旧的知识，这个节奏比较合适一点，或者学习两天新的知识，复习一天旧的知识。两天太少了，到时候正常的进度都复习不完。还是三天吧。今天算是学习新知识的一天，10 号，11、12 都学习新的知识，等到 13 号，那一整天，就复习之前复习过的内容。这样可能最后的效果更好一点。

强化 63

这题有点难度，但是看了一下讲解，感觉纯送分的。戒骄戒躁慢慢来。实际上考察的是基础知识，幂函数的图像，第三幅图，趋近于零的时候极限是零。指数为正数。

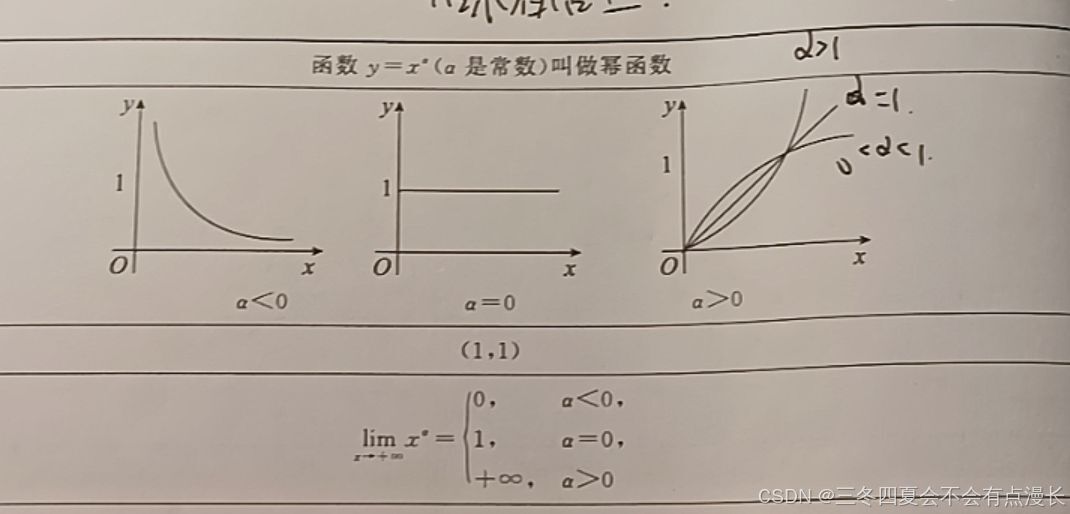
在这里插入图片描述

然后感觉可以积累一下这个题的解题过程。假设，我们算出来了一个导数，分段点外初等函数是可以直接求导算出来导数的，要求导数连续，🤔，分段点上导数实际上是一个确定的数字，我们用导数定义算出来左导数和右导数，然后让它们相等，这就说明了这个点的导数的存在，还需要满足这个点的导数的极限等于导数的函数值。一个振荡的函数，怎么能让它的极限为零，只有乘上一个无穷小量，所以就解决问题了，周洋鑫很喜欢出这个类型的题，他可能是预测这个是考试的重点。

导数在某点连续，该点左导数和右导数相等即可。然后根据导数极限定理，左导数等于导数一侧的去心邻域的极限，右导数等于导数另一侧去心邻域的极限，让这两个极限相等，即可，这题为啥满足导数极限定理呢。首先是，函数在这个点，具体这个题就是 0 这个点，肯定是连续的，因为 0 这个点导数都是连续的，那么 0 这个点是可导的，可导必连续。然后，函数去心邻域是可导的，两侧的导数都是可以写出表达式的，说明肯定是可以求导的，那么最后一个，函数在 0 的去心邻域内的导数的极限是不振荡的，首先导数在 0 处连续，那么导数在这个点处的极限等于 0 处的导数值，导数在 0 的某个邻域内的极限就是导数值，就是唯一的，极限存在必唯一，应该可以了。然后这个问题就非常简单了。老师讲解得非常到位，高山看海，不要退缩，菜就多练就可以了。dedicated to myself.

24 year real question

这题应该是选第二个选项。首先，只给了我们有定义，对了，老师讲的很对，不会就学，就练习，就思考，冷静地思考，而不是否定自己，不要怀疑自己的智商和学习能力。没有告诉我们函数是连续的，所以 0 处的函数值是未知的，所以第一个选项不对。第二个应该是对的。0 处可导，那么 0 处连续，0 处的函数值等于极限，是连续的，然后导数定义写出来，就可以第二个选项。第三个选项，和第四个选项，试图考察导数极限定理，但是都没有满足严格的条件。导数极限定理，要求函数在 0 处是连续的，第三个选项没有保证连续的条件。第四个选项，一点可导，不能推出邻域内是可导的，导数极限定理要求邻域内是可导的。

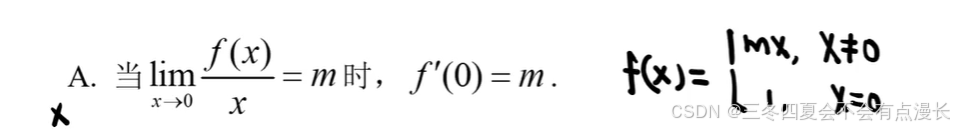
这个反例可以积累一下。不连续一定不可导。连续是可导的必要条件。实际上这块是逆否命题，逆否命题就是条件和结论都相反，然后交换条件和结论。非常有意思。互为逆否命题的两个命题的真假性是一致的。比如说，可导一定连续，逆否命题是，不连续一定不可导，振荡一定是极限不存在，极限存在一定是不振荡。绕清楚了🙁

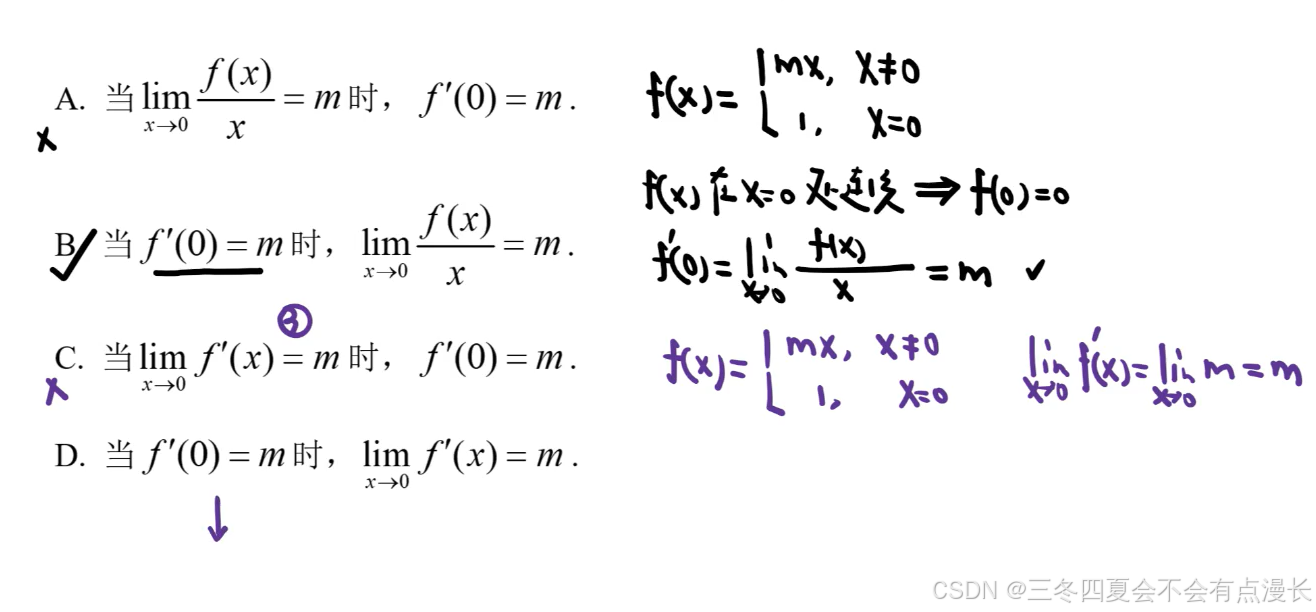
在这里插入图片描述

第三个选项的例子也很可以，感觉自己举反例的能力还有待提升。

在这里插入图片描述

振荡的经典函数！ $f(x)=x2sin⁡1xf(x)=x^2\sin\frac1x$ ，可以多积累积累。

强化 64

这题也很有操作性。因为，分段点求出来导数之后，为啥要取极限呢。因为我们要判断导数是否连续，就要判断导数的极限值和导数值是否相等，导数值我们已经算出来了，然后算一个导数的极限值就可以了。

supplement

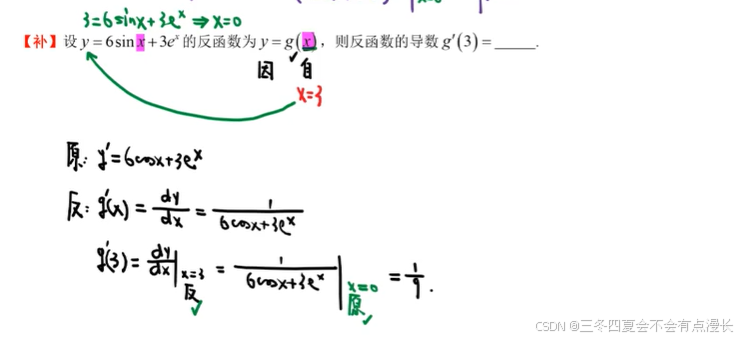
在这里插入图片描述

这里是第二类反函数。第一类反函数是 $x=f^{-1}(y)$ , 第二类反函数是 $y=f^{-1}(x)$ ,这个不重要，重要的是，它们都是反函数，反函数的自变量，都是原来函数的因变量。

66

老师说得很对，有时间多复盘和消化吸收，比什么都重要。这题就是考察了反函数的求导公式。 $dxdy=1f′(x),d2xdy2=−f′′(x)[f′(x)]3\frac{dx}{dy}=\frac1{f'(x)},\frac{d^2x}{dy^2}=\frac{-f''(x)}{[f'(x)]^3}$ ，然后反函数自变量和原来函数因变量是一致的。就可以了。