LeetCode131~150题解
LeetCode131.分割回文串:
题目描述:
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是
回文串
。返回 s 所有可能的分割方案。
示例 1:
输入:s = “aab”
输出:[[“a”,“a”,“b”],[“aa”,“b”]]
示例 2:
输入:s = “a”
输出:[[“a”]]
提示:
1 <= s.length <= 16
s 仅由小写英文字母组成
思路:
一看这种数据很短,但是看起来比较复杂的问题,就揪一下它的最大可能次数: 比如字符串长度为n,且全是相同字母,那么方案数是需要在n-1个空中任意组合,每个空可以分割或者不分割,总的方案数最坏情况是2^(n-1),是指数级别的,那么就可以断定是爆搜问题。
对于这题来说,我们可以先扫描一遍,判断哪些段[i ~ j]是回文段是可以的,但更好的做法是用一个数组来存储原字符串中i~j是否为回文串f[i][j]: 递归来做,f[i][j]为回文串,前提是s[i] == s[j] 并且 f[i + 1][j - 1]已经是回文串了,以此递推下去,将整个原字符串中所有回文段全部存储下来,但是这里有个需要注意的就是f[i][j]是由f[i + 1][j - 1]推出来的,所以我们需要先求出f[i + 1][j - 1],同时j是在i的后面的, 所以我们先枚举j!!!(细节很重要)
dfs:爆搜:由于已经记录了原字符串中i ~j 是否为回文串,所以我们从第0个字符开始搜索所有方案,从前往后枚举每一个字符,只要枚举到的位置跟开始位置之间的字符段是回文串,那么就将它截取出来放到当前搜索路径中,同时进入下一层搜索(从当前枚举的位置的下一个位置开始),将当前搜索完之后一定要记得将当前路径加入的当前字符段清掉,恢复现场, 保证下一段回文段的搜索不被打乱
当搜到s的最后一个字符就是结束,将整条搜索路径加入答案集合中
时间复杂度:
首先考虑最多有多少个合法方案,我们可以考虑在相邻字符之间放板子,每种放板子的方法都对应一种划分方案,而每个字符间隔有放和不放两种选择,所以总共有 2^n−1
个方案。另外对于每个方案,需要 O(n)的时间记录方案。所以总时间复杂度是 O(2^n)*n
注释代码:
class Solution {
public:vector<vector<bool>> f;vector<vector<string>> res;vector<string> path;vector<vector<string>> partition(string s) {int n = s.size();//f[i][j]表示原字符串的i~j这段是否为回文串f = vector<vector<bool>> (n, vector<bool>(n));for(int j = 0; j < n; j++) //要先求出f[i + 1][j - 1]所以先枚举j{for(int i = 0; i <= j; i++){if(i == j) f[i][j] = true; //只有一个单词肯定是回文串else if(s[i] == s[j]){//只有两个字符(还相同),或者是原字符串中i+ 1 ~ j - 1是回文串,那么f[i][j]肯定也是回文串if(i + 1 > j - 1 || f[i + 1][j - 1]) f[i][j] = true;}}}dfs(s, 0); //找出所有方案,从第0个字符开始搜return res;}void dfs(string&s, int u){if(u == s.size()) res.push_back(path);else{for(int i = u; i < s.size(); i++){if(f[u][i]){path.push_back(s.substr(u, i - u + 1));dfs(s, i + 1);path.pop_back();}}}}
};
纯享版:
class Solution {
public:vector<vector<bool>> f;vector<string> path;vector<vector<string>> res;vector<vector<string>> partition(string s) {int n = s.size();f = vector<vector<bool>> (n, vector<bool> (n));for(int j = 0; j < n; j++){for(int i = 0; i <= j; i++){if(i == j) f[i][j] = true;else if(s[i] == s[j]){if(i + 1 > j - 1 || f[i + 1][j - 1]) f[i][j] = true;}}}dfs(s, 0);return res;}void dfs(string& s, int u ){if(u == s.size()) res.push_back(path);else{for(int i = u; i < s.size(); i++){if(f[u][i]){path.push_back(s.substr(u, i - u + 1));dfs(s, i + 1);path.pop_back();}}}}
};
LeetCode132.分割回文串Ⅱ:
题目描述:
###一开始直接考虑使用上题的path.size()进行判断,但是上一题的时间复杂度是O(2^n * n),会超时,所以爆搜方案肯定是不能用的,需要使用DP优化:用一个状态来表示一种方案
class Solution {
public:vector<vector<bool>> f;int res = INT_MAX;vector<string> path;int minCut(string s) {int n = s.size();//f[i][j]表示原字符串的i~j这段是否为回文串f = vector<vector<bool>> (n, vector<bool>(n));for(int j = 0; j < n; j++) //要先求出f[i + 1][j - 1]所以先枚举j{for(int i = 0; i <= j; i++){if(i == j) f[i][j] = true; //只有一个单词肯定是回文串else if(s[i] == s[j]){//只有两个字符(还相同),或者是原字符串中i+ 1 ~ j - 1是回文串,那么f[i][j]肯定也是回文串if(i + 1 > j - 1 || f[i + 1][j - 1]) f[i][j] = true;}}}dfs(s, 0); //找出所有方案,从第0个字符开始搜return res;}void dfs(string&s, int u){if(u == s.size()){int t = path.size();if(t > 0) res = min(res, t - 1);}else{for(int i = u; i < s.size(); i++){if(f[u][i]){path.push_back(s.substr(u, i - u + 1));dfs(s, i + 1);path.pop_back();}}}}
};思路:
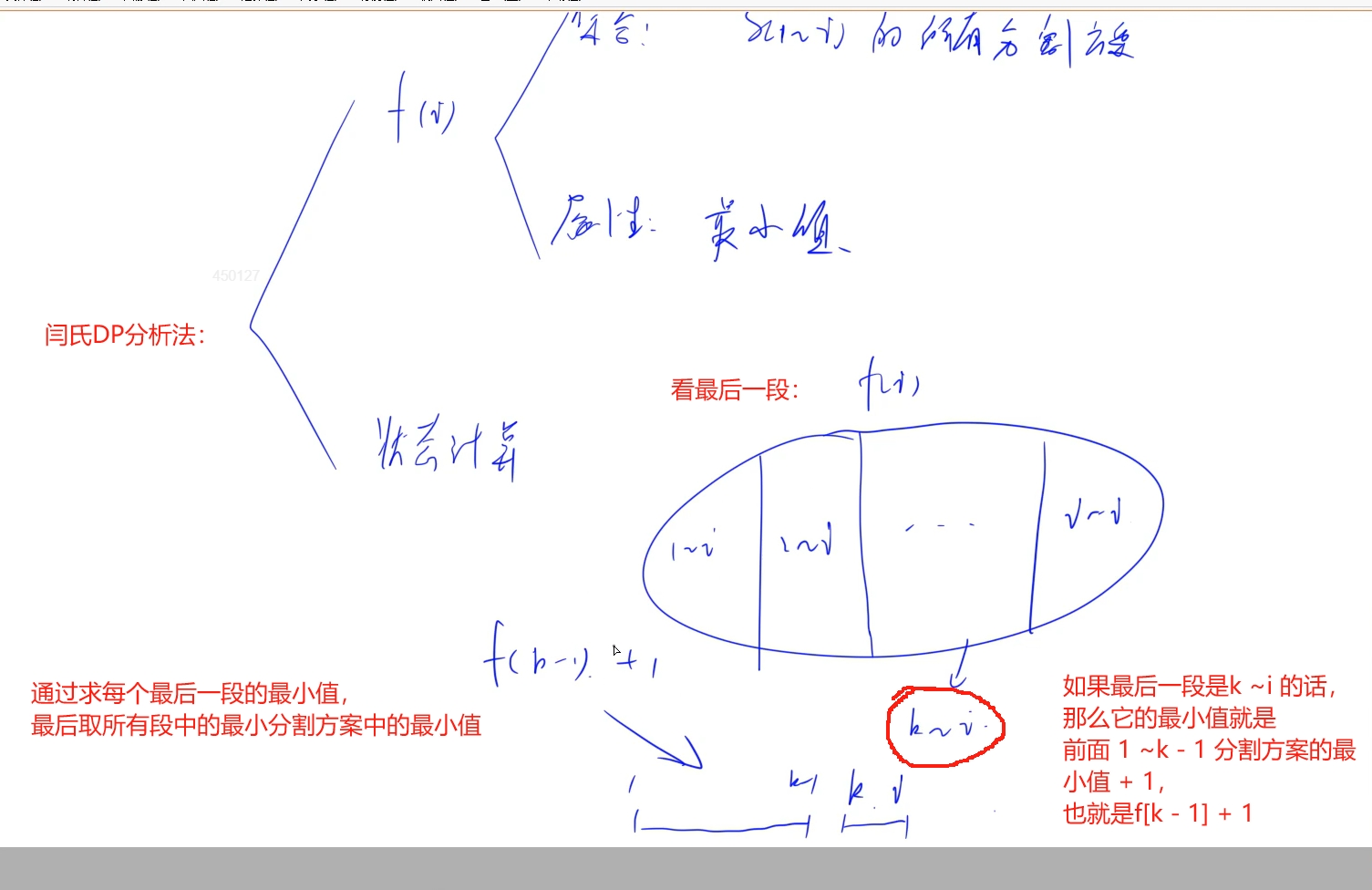
使用DP优化:用一个状态来表示一种方案=>设定集合f[i]: s[1~i]的所有分割方案,属性是最小值: 利用上一题的确定回文段的维护数组,在s[1 ~i]中的所有分割方案就是根据回文段数组来分割的,那么1 ~ i的分割方案求最小值的状态划分以最后一段回文段来划分,比如k ~i,那么1 ~i的最小分割方案就是1 ~ k -1的最小方案数加当前最后一段: f[i] = f[k -1] + 1
时间复杂度:
求回文段数组O(nn), DP状态也是O(nn)的,所以总的时间复杂度是O(n*n)的

注释代码:
class Solution {
public:int minCut(string s) {int n = s.size();s = ' ' + s;vector<vector<bool>> g(n + 1, vector<bool>(n + 1));vector<int> f(n + 1, 1e8);for(int j = 1; j <= n; j++){for(int i = 1; i <= n; i++){if(i == j) g[i][j] = true;else if(s[i] == s[j]){if(i + 1 > j - 1 || g[i + 1][j - 1]) g[i][j] = true;}}}f[0] = 0;for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){if(g[j][i]) //j在前i在后{//如果j ~ i 这段是回文段的话,将它作为最后一段,那么f[i] = f[j - 1] + 1f[i] = min(f[i], f[j - 1] + 1);}}}return f[n] - 1;}
};纯享版:
class Solution {
public:int minCut(string s) {int n = s.size();s = ' ' + s;vector<vector<bool>> g(n + 1, vector<bool> (n + 1));vector<int> f(n + 1, 1e8);for(int j = 1; j <= n; j++){for(int i = 1; i <= j; i++){if(i == j) g[i][j] = true;else if(s[i] == s[j]){if(i + 1 > j - 1 || g[i + 1][j - 1]) g[i][j] = true;}}}f[0] = 0;for(int i = 1; i <= n; i++){for(int j = 1; j <= i; j++){if(g[j][i]){f[i] = min(f[i], f[j - 1] + 1);}}}return f[n] - 1;}
};LeetCode133.克隆图:
题目描述:
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List neighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
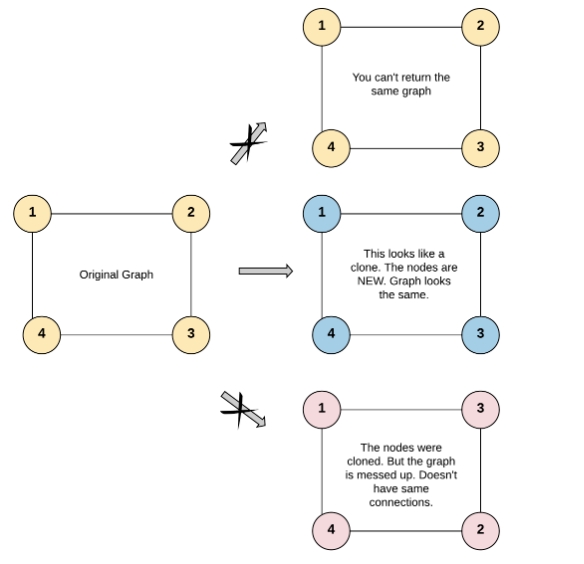
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
示例 2:

输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。
提示:
这张图中的节点数在 [0, 100] 之间。
1 <= Node.val <= 100
每个节点值 Node.val 都是唯一的,
图中没有重复的边,也没有自环。
图是连通图,你可以从给定节点访问到所有节点。
思路:
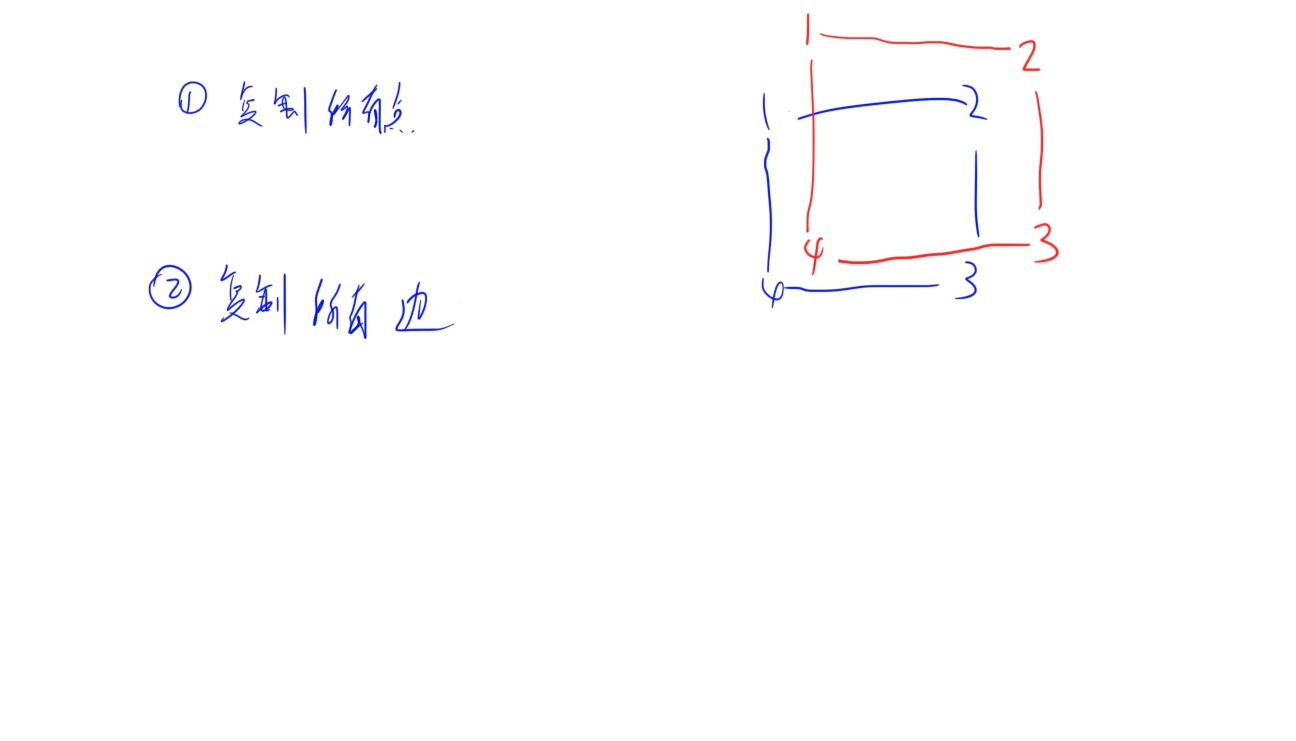
先复制所有点,在将每个点之间的边复制下来
时间复杂度:每个点每条边遍历一次,时间复杂度是O(m)的,m为边数
注释代码:
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> neighbors;Node() {val = 0;neighbors = vector<Node*>();}Node(int _val) {val = _val;neighbors = vector<Node*>();}Node(int _val, vector<Node*> _neighbors) {val = _val;neighbors = _neighbors;}
};
*/class Solution {
public:unordered_map<Node*, Node*> hash; //存点的映射Node* cloneGraph(Node* node) {if(!node) return NULL;dfs(node); //复制所有点for(auto [s, d] : hash) //取出每个点及其映射{for(auto ver : s -> neighbors) //找出遍历到的点的所有邻点 ,(存在的边){d -> neighbors.push_back(hash[ver]); //将所有邻点同样添加为映射的邻点,相当于建边}}return hash[node];}void dfs(Node* node){hash[node] = new Node(node -> val); //复制当前点到hash中并一起存储下来for(auto ver : node -> neighbors) //遍历当前点的所有邻点{if(hash.count(ver) == 0) //如果当前的邻点没有复制过{dfs(ver); //递归下去}}}
};
纯享版:
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> neighbors;Node() {val = 0;neighbors = vector<Node*>();}Node(int _val) {val = _val;neighbors = vector<Node*>();}Node(int _val, vector<Node*> _neighbors) {val = _val;neighbors = _neighbors;}
};
*/class Solution {
public:unordered_map<Node*, Node*> hash;Node* cloneGraph(Node* node) {if(!node) return NULL;dfs(node);for(auto [s, d] : hash){for(auto ver : s -> neighbors){d -> neighbors.push_back(hash[ver]);}}return hash[node];}void dfs(Node* node){hash[node] = new Node(node -> val);for(auto ver : node -> neighbors){if(hash.count(ver) == 0){dfs(ver);}}}
};
2024/12/13二刷:
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> neighbors;Node() {val = 0;neighbors = vector<Node*>();}Node(int _val) {val = _val;neighbors = vector<Node*>();}Node(int _val, vector<Node*> _neighbors) {val = _val;neighbors = _neighbors;}
};
*/class Solution {
public:unordered_map<Node*, Node*> hash;Node* cloneGraph(Node* node) {if(!node) return NULL;dfs(node);for(auto [s, t] : hash){for(auto ver : s -> neighbors){t -> neighbors.push_back(hash[ver]);}}return hash[node];}void dfs(Node* node){hash[node] = new Node(node -> val);for(auto s : node -> neighbors){if(hash.count(s) == 0) dfs(s);}}
};LeetCode134.加油站:
题目描述:
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
gas.length == n
cost.length == n
1 <= n <= 10^5
0 <= gas[i], cost[i] <= 10^4
思路:
正常遍历每个站的每个状态是n*n的,会超时,

时间复杂度:
虽然两重循环,但是i是靠j来更新的,每次i跳到i+j+1的位置,所以相当于只循环了n次,总的时间复杂度是O(n)的
注释代码:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();for(int i = 0, j; i < n;) //枚举起点{int left = 0; //剩余油量for(j = 0; j < n; j++) //往后走的站点数{int k = (i + j) % n; //当前在哪个站left += gas[k] - cost[k]; //剩余油量减去当前站加的油和去往下一站消耗的油量if(left < 0) break;}if(j == n) return i; //如果j 为n,说明以当前i为起点站,往后走n个站都能走通,说明已经绕了一圈i = i + j + 1; //否则说明left小于0 了,意味着从当前i走不到i+ j, 且i~i + j都无法作为起点站绕以前}return -1;}
};
纯享版:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int n = gas.size();for(int i = 0, j; i < n;){int left = 0;for(j = 0; j < n; j++){int k = (i + j) % n;left += gas[k] - cost[k];if(left < 0) break;}if(j == n) return i;i = i + j + 1;}return -1;}
};
LeetCode135.分发糖果:
题目描述;
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
提示:
n == ratings.length
1 <= n <= 2 * 10^4
0 <= ratings[i] <= 2 * 10^4
思路:
跟acwing901滑雪问题很类似,对于每个位置上的孩子该分发的糖果数量往左右两侧进行递归搜索

时间复杂度:
每个孩子分发的糖果数量只会计算一次,计算时间是O(1)的,总时间复杂度是O(n)的
注释代码:
class Solution {
public:vector<int> f;vector<int> w;int n;int candy(vector<int>& ratings) {n = ratings.size();w = ratings;f.resize(n, -1);int res = 0;for(int i = 0; i < n; i++) res += dp(i); //依次求每个位置上的孩子糖果数进行累加return res;}int dp(int x) //返回当前位置上孩子需要分配的糖果最大数量{if(f[x] != -1) return f[x];f[x] = 1; //初始为1颗if(x && w[x - 1] < w[x]) f[x] = max(f[x], dp(x - 1) + 1); //x不为0,并且当前分值高于左边孩子,那么他的糖果数量是左边孩子需要分配的糖果最大数量+1if(x + 1 < n && w[x + 1] < w[x]) f[x] = max(f[x], dp(x + 1) + 1); //当前分值高于右边孩子,那么他的糖果数量是右边孩子需要分配的糖果最大数量+1return f[x];}
};
纯享版:
class Solution {
public:int n;vector<int> f;vector<int> w;int candy(vector<int>& ratings) {n = ratings.size();w = ratings;int res = 0;f.resize(n, -1);for(int i = 0; i < n; i++) res += dp(i);return res;}int dp(int x){if(f[x] != -1) return f[x];f[x] = 1;if(x && w[x - 1] < w[x]) f[x] = max(f[x], dp(x - 1) + 1);if(x + 1 < n && w[x + 1] < w[x]) f[x] = max(f[x], dp(x + 1) + 1);return f[x];}
};LeetCode136.只出现一次的数字:
题目描述:
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1]
输出:1
示例 2 :
输入:nums = [4,1,2,1,2]
输出:4
示例 3 :
输入:nums = [1]
输出:1
提示:
1 <= nums.length <= 3 * 10^4
-3 * 10^4 <= nums[i] <= 3 * 10^4
除了某个元素只出现一次以外,其余每个元素均出现两次。
思路:
要求使用O(n)时间复杂度,而且常量空间,由于每个元素出现两次,只有一个出现一次,那么可以使用异或来做, 因为 a^a = 0, a ^ 0 = a,相同元素异或为0, 最后只剩下单独的一个元素,就是我们要找的元素
时间复杂度:O(n)
注释代码:
class Solution {
public:int singleNumber(vector<int>& nums) {int res = 0;for(int i = 0; i < nums.size(); i++) res ^= nums[i]; //0^a=areturn res;}
};LeetCode137.只出现一次的数字Ⅱ:
题目描述:
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
1 <= nums.length <= 3 * 10^4
-2^31 <= nums[i] <= 2^31 - 1
nums 中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
思路:
时间复杂度:O(n)
注释代码:
class Solution {
public:int singleNumber(vector<int>& nums) {int two = 0, one = 0;for(auto x : nums){one = (one ^ x) & ~two;two = (two ^ x) & ~one;}return one;}
};LeetCode138.复制带随机指针的链表:
题目描述:
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:

输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
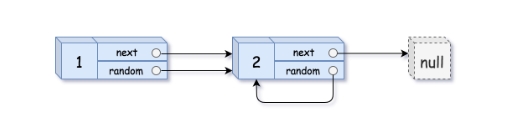
输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:
输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
提示:
0 <= n <= 1000
-10^4 <= Node.val <= 10^4
Node.random 为 null 或指向链表中的节点。
思路;
时间复杂度:
每个节点遍历三次,每个节点时间消耗是O(1)的,总的时间复杂度是O(n)的,空间复杂度为O(1)
注释代码:
/*
// Definition for a Node.
class Node {
public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}
};
*/class Solution {
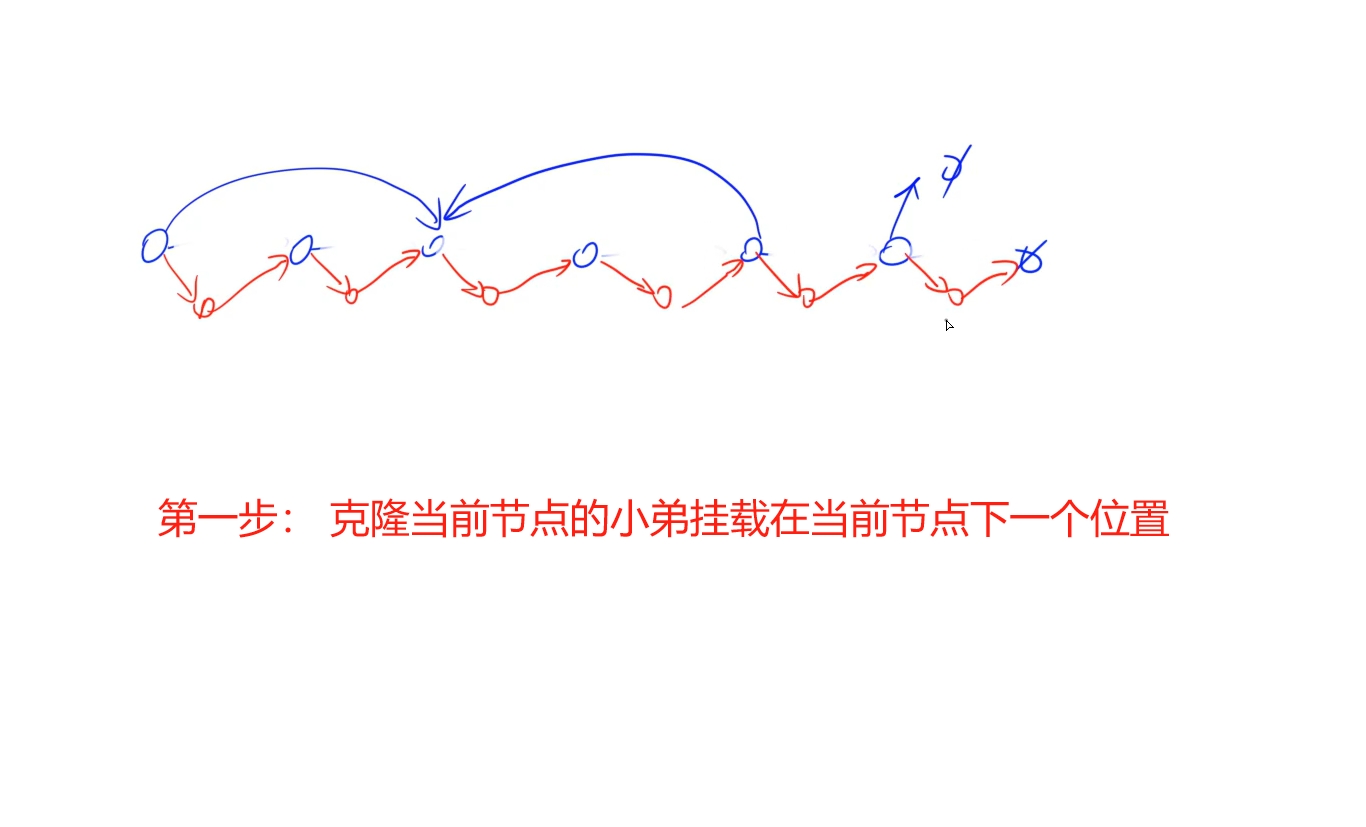
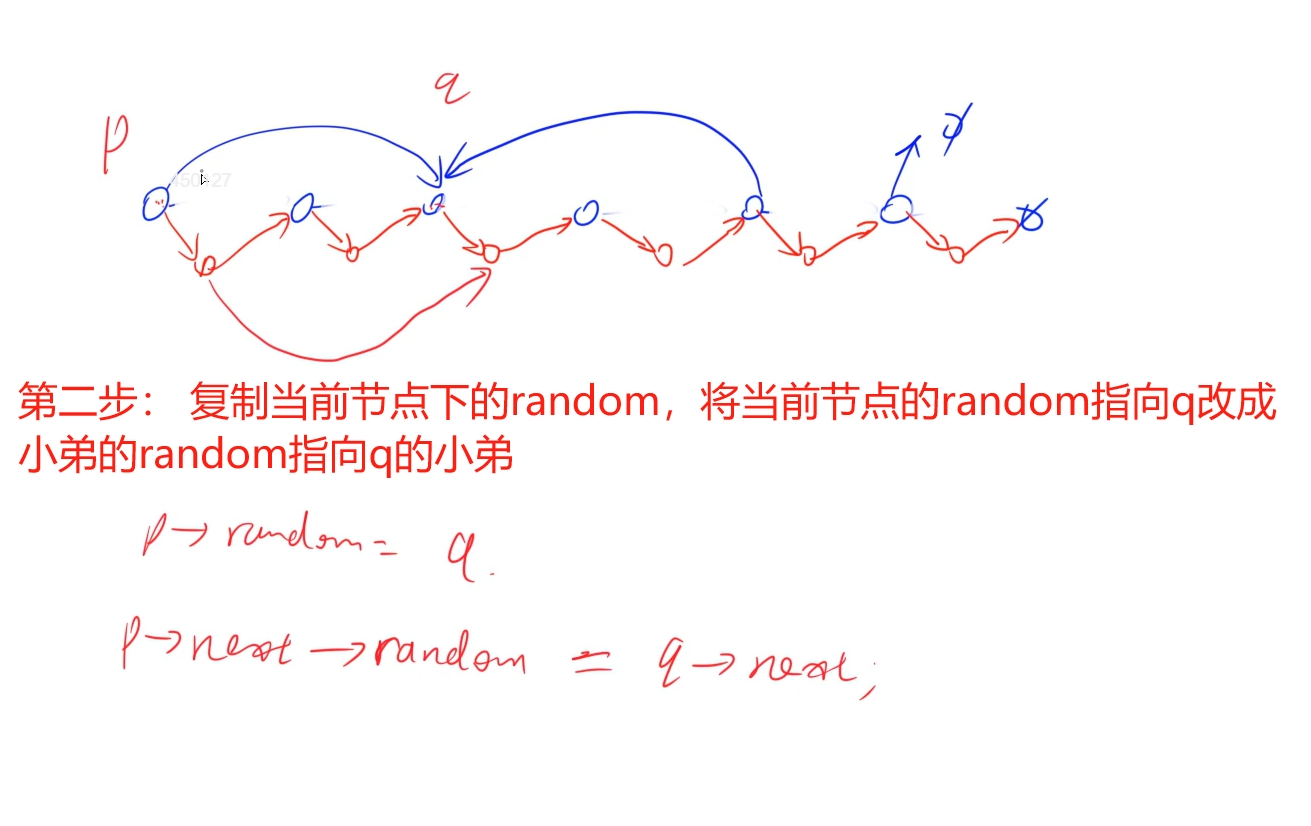
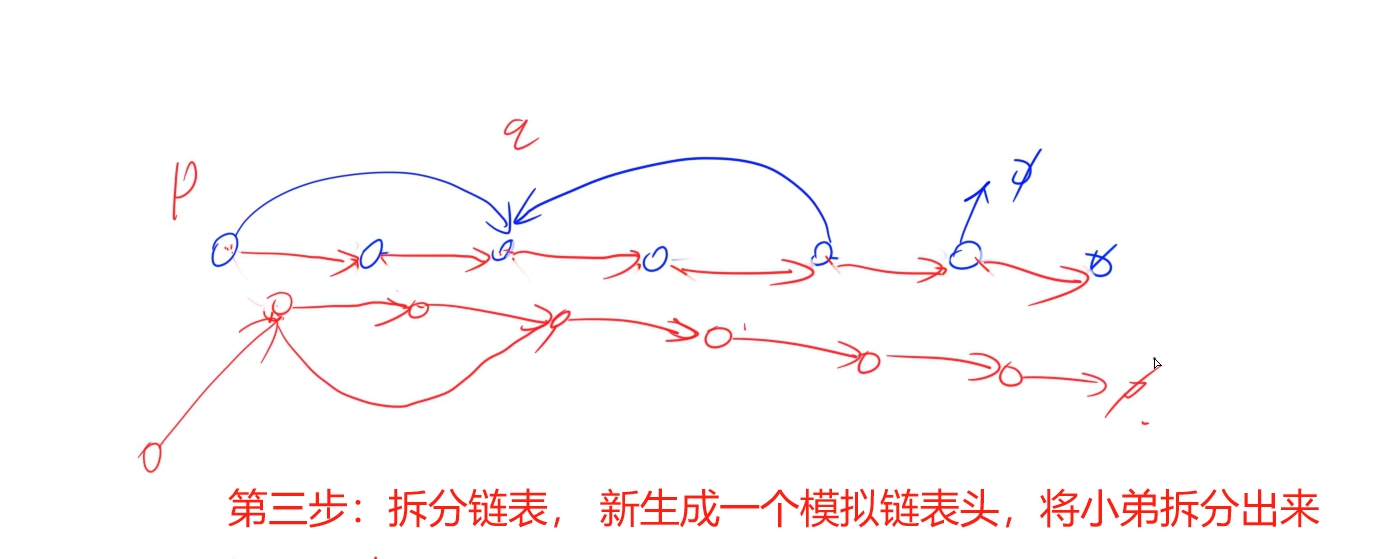
public:Node* copyRandomList(Node* head) {for(auto p = head; p; p = p -> next -> next){auto q = new Node(p -> val); //复制小弟,挂载在当前节点的下一个位置q -> next = p -> next;p -> next = q;}for(auto p = head; p; p = p -> next -> next){if(p -> random){p -> next -> random = p -> random -> next; //复制random}}auto dummy = new Node(-1), cur = dummy;for(auto p = head; p; p = p -> next) //拆分链表{auto q = p -> next;cur = cur -> next = q; p -> next = q -> next;}return dummy -> next;}
};
纯享版:
hash做法:
时间复杂度O(n), 空间复杂度O(n)
/*
// Definition for a Node.
class Node {
public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}
};
*/class Solution {
public:unordered_map<Node*, Node*> hash;Node* copyRandomList(Node* head) {if(!head) return head;if(hash.count(head)) return hash[head];auto dummy = new Node(head -> val);hash[head] = dummy;dummy -> next = copyRandomList(head -> next);dummy -> random = copyRandomList(head -> random);return dummy;}
};LeetCode139.单词拆分:
题目描述:
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅由小写英文字母组成
wordDict 中的所有字符串 互不相同
思路:
动态规划思路:看s的1~i个字符中是否能进行合法划分f[i],也就是能将s进行划分,分成字典中包含的单词,那么我们每次看最后一个单词长度, i~i:0个字母组成、 i-1 ~i:单个字母组成、i-2 i、…、1i, 同时可以发现 f[i]等于f[1~k-1] && s[k~i]在字典中,以此来判断s字符串能不能进行划分成字典中的单词也就是f[n]为真(n为s长度)
状态表示-集合:f[i]表示字符串s的1…i的所有合法划分方案。
状态表示-属性:f[i]的值表示集合是否非空,即是否具有从1…i的合法划分。
集合划分:按照f[i]集合中的最靠后的一个单词是i…i、i−1…i、…、1…i来划分成若干子集,在确保最后一个单词是合法(在字典中出现过)的时候,来检查是否有一个子集非空(前面的部分f[k−1]是否是true)就行了,只要有一个子集非空那么f[i]就是非空的。
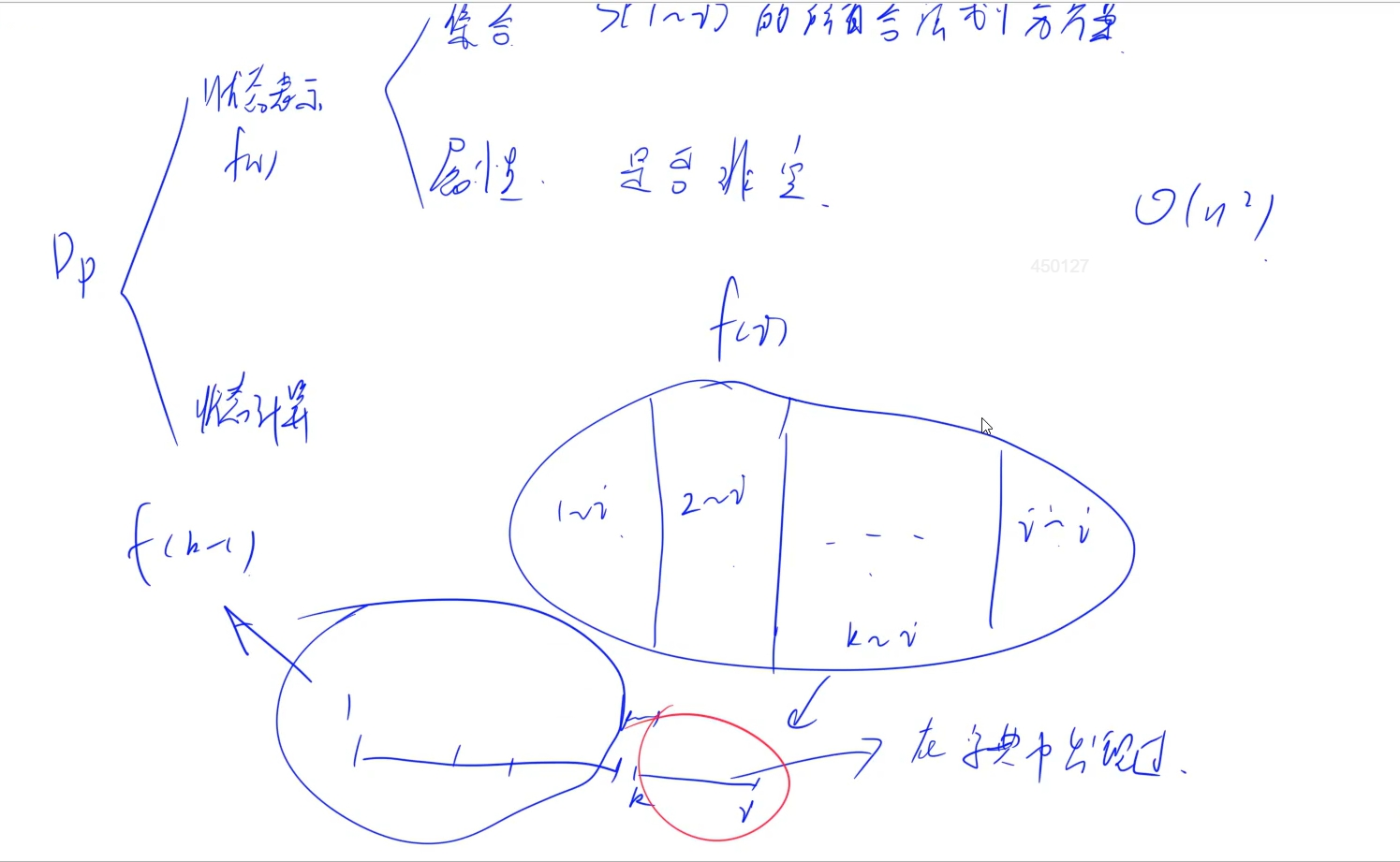
再考虑检查字符串是不是在字典中出现过这件事,如果用STL哈希表来做,因为STL中的哈希表存字符串时候,查询的时间是和字符串成正比的,所以这样做的话整个时间复杂度就是O(n3)
考虑优化一下查询字符串在字典中这件事,有几种方案:
- Trie树,平均是O(1)的
- 手写字符串哈希
- KMP
这里用手写字符串哈希的方式,将一个字符串转化成一个数字,那么在哈希表中查询数字的时间复杂度就是O(1)的了。
字符串哈希就是将一个字符串看成一个P进制数,比如abcde就可以看成一个5位的P进制数,得到的数可能很大,那么就模上一个数Q,即:
(a×P4+b×P3+c×P2+d×P1+e×P0) mod Q
经验值:P一般取131、13331,Q一般取264,模上这个264之后也就可以用无符号长整型unsigned long long来存储了(不用考虑取模,因为溢出了会自动模2^64)。实践证明这样取值几乎不会冲突。
因为每一段子串都要算哈希值,如果先算了3…4的值是h,那么3…5的值就能很快算出来,就是h×P+s[5],为了能做到这一点,可以先从小到大枚举前面的部分的f[i],想要看看它为真能够导致哪些状态为真(而不是反过来),对于每个为true的f[i]
枚举i+1…j这一段(让j不断增加),只要i+1…j这一段是合法的(在哈希表里能找到),那么就说明f[j]是true,给它赋值。
最后答案就是f[n]
时间复杂度:
字符串哈希O(1), dp找f[i]的合法方案是O(nn)的,总的时间复杂度是O(nn)的
注释代码:
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {typedef unsigned long long ULL;const int P = 131;unordered_set<ULL> hash;for(auto& word : wordDict) //先计算出字典中每一个单词的哈希数值指代{ULL h = 0;for(auto c : word) h = h * P + c; //计算word中每一个前缀的代表数值hash.insert(h); //插入数值到哈希表中}int n = s.size();vector<bool> f(n + 1); //s[1 ~ i]的所有合法划分方案f[0] = true;s = ' ' + s;// 前面一段是f[i],最后一段是i+1..jfor(int i = 0; i < n; i++) {if(f[i]) // 如果从1..i是有划分方法的,再去看f[i]为真会导致哪些f[j]为真(当前状态可以推到那些状态){ULL h = 0;for(int j = i + 1; j <= n; j++){h = h * P + s[j]; //计算从i + 1 到j的字符串的哈希数值指代//f[i]为真,并且i + 1 ~ j在字典中是存在的,说明f[j]是肯定合法的if(hash.count(h)) f[j] = true; //如果当前i+ 1 ~j出现过的话,说明f[j]为true}}}return f[n];}
};纯享版:
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {typedef unsigned long long ULL;unordered_set<ULL> hash;const int P = 131;int n = s.size();vector<bool> f(n + 1);for(auto& word : wordDict){ULL h = 0;for(auto c : word){h = h * P + c;}hash.insert(h);}f[0] = true;s = ' ' + s;for(int i = 0; i < n; i++){if(f[i]){ULL h = 0;for(int j = i + 1; j <= n; j++){h = h * P + s[j];if(hash.count(h)) f[j] = true;}}}return f[n];}
};LeetCode140.单词拆分Ⅱ:
题目描述:
给定一个字符串 s 和一个字符串字典 wordDict ,在字符串 s 中增加空格来构建一个句子,使得句子中所有的单词都在词典中。以任意顺序 返回所有这些可能的句子。
注意:词典中的同一个单词可能在分段中被重复使用多次。
示例 1:
输入:s = “catsanddog”, wordDict = [“cat”,“cats”,“and”,“sand”,“dog”]
输出:[“cats and dog”,“cat sand dog”]
示例 2:
输入:s = “pineapplepenapple”, wordDict = [“apple”,“pen”,“applepen”,“pine”,“pineapple”]
输出:[“pine apple pen apple”,“pineapple pen apple”,“pine applepen apple”]
解释: 注意你可以重复使用字典中的单词。
示例 3:
输入:s = “catsandog”, wordDict = [“cats”,“dog”,“sand”,“and”,“cat”]
输出:[]
提示:
1 <= s.length <= 20
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 10
s 和 wordDict[i] 仅有小写英文字母组成
wordDict 中所有字符串都 不同
思路:
还是动态规划思想:这里跟上题类似,只不过他需要爆搜所有路径,将存在于字典中的可以拼成s字符串的单词

时间复杂度:
substr是O(n)的,动态规划的时间复杂度是O(nn)的,所以总的时间复杂度是O(n^3)
注释代码:
class Solution {
public:vector<bool> f;vector<string> res;unordered_set<string> hash;int n;vector<string> wordBreak(string s, vector<string>& wordDict) {n = s.size();f.resize(n + 1); //f[i]表示s[i ~n]能否进行合法划分,使得每一部分都在字典中出现for(auto word : wordDict) hash.insert(word); //将字典中的单词存入hash表//从后往前处理i~n的状态f[n] = true;for(int i = n - 1; i >= 0; i--){for(int j = i; j < n; j++) //起点{//如果i~j + 1是存在于字典中的,并且f[j + 1]是合法的,那么说明f[i]是合法的if(hash.count(s.substr(i, j - i + 1)) && f[j + 1]) //为什么要从后往前,因为f[j+1]是要比f[i]先计算出来{f[i] = true;}}}dfs(s, 0, ""); //爆搜所有方案return res;}void dfs(string& s, int u, string path){if(u == n){path.pop_back(); //每次添加后面都加了一个空格,所以最后面会多出一个空格res.push_back(path);}else{for(int i = u; i < n; i++) //从当前字符开始往后遍历{if(hash.count(s.substr(u, i - u + 1)) && f[i + 1]) //如果u~i是包含在字典中并且f[i+1]是可以划分的{dfs(s, i + 1, path + s.substr(u, i - u + 1) + ' '); //那么往i+1开始搜,并且将u~i加到当前搜的路径中,后面加个空格}}}}
};纯享版:
class Solution {
public:vector<bool> f;unordered_set<string> hash;vector<string> res;int n;vector<string> wordBreak(string s, vector<string>& wordDict) {n = s.size();for(auto& word : wordDict) hash.insert(word);f.resize(n + 1);f[n] = true;for(int i = n - 1; i >= 0; i--){for(int j = i; j < n; j++){if(hash.count(s.substr(i, j - i + 1)) && f[j + 1]){f[i] = true;}}}dfs(s, 0, "");return res; }void dfs(string& s, int u, string path){if(u == n){path.pop_back();res.push_back(path);}else{for(int i = u; i < n; i++){if(hash.count(s.substr(u, i - u + 1)) && f[i + 1]){dfs(s, i + 1, path + s.substr(u, i - u + 1) + ' ');}}}}
};LeetCode141.环形链表:
题目描述:
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
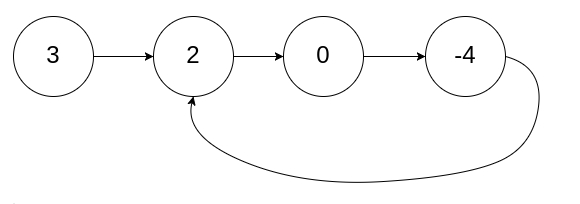
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
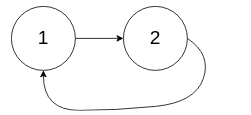
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
链表中节点的数目范围是 [0, 10^4]
-10^5 <= Node.val <= 10^5
pos 为 -1 或者链表中的一个 有效索引 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
思路:
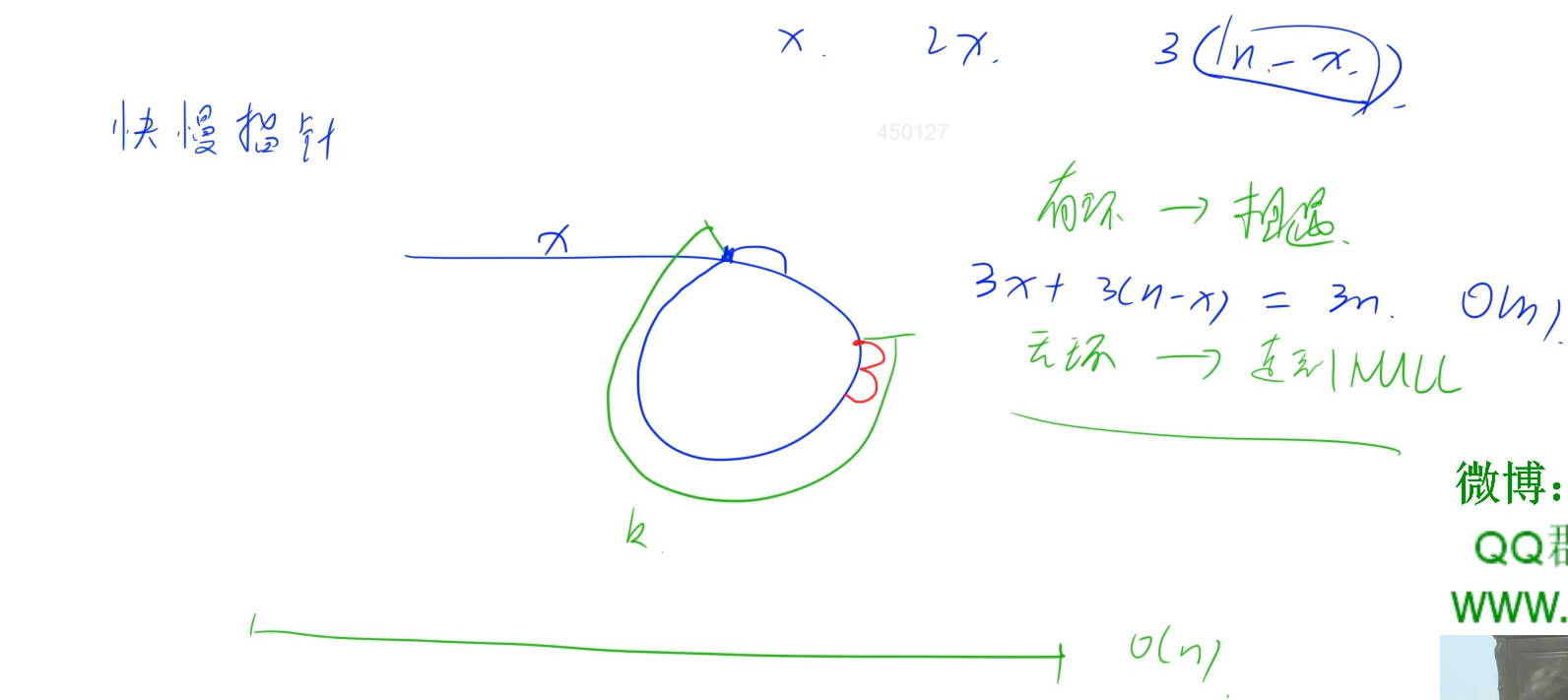
快慢指针: 快指针每次走两次,慢指针每次走一次,当链表中存在环时,会发现快指针会先进入环内,那么在慢指针进入环内开始,每走一次,快指针就会缩小和慢指针之间的差距,直到追上慢指针。
时间复杂度:
1.无环链表: 快指针会最先走完整个链表,每个节点走过一次,时间复杂度是O(n)的
2.有环链表: 假设链表长度为n,慢指针在走x之后进入环,那么此时快指针走了2x步,并且已经进入环内,那么此时快慢指针的距离最大为n-x, 由于此时每走一步快慢指针距离缩小1, 所以再走n-x步就能相遇,那么慢指针会走n-x步,快指针则会走2(n-x)步,所以总的时间复杂度为: x + 2x + (n-x) + 2(n-x) = O(n)
注释代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {if(!head || !head -> next) return false; //如果为空或者只有一个节点并且没有next则不存在环auto s = head, f = head -> next; //s:慢指针 f: 快指针while(f) //当前快指针不为空{s = s -> next, f = f -> next; //均往后移动一步if(!f) return false; //如果快指针走到空了,说明已经到链表尾部f = f -> next; //否则快指针再走一步if(s == f) return true; //如果二者相遇了,说明存在环}return false;}
};纯享版:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {if(!head || !head -> next) return false;auto s = head, f = head -> next;while(f){s = s -> next, f = f -> next;if(!f) return false;f = f -> next;if(s == f) return true;}return false;}
};LeetCode142.环形链表Ⅱ:
题目描述:
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 10^4] 内
-10^5 <= Node.val <= 10^5
pos 的值为 -1 或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
思路:
思路比较巧妙: 假设慢指针从起点a经过x步到达环入口b处,而快慢指针的相遇点c距离环入口距离为y,那么通过回推,也就是将慢指针往回移动y步回退到环入口b处,此时的快指针则位于d点(快指针在慢指针到达环入口b处时的位置),而d到b的距离则为y(因为慢指针移动y步,快指针移动2y步),而因为a到b的距离为x,那么快指针在慢指针从a移动到b走了x步时,快指针走了2x步到了d,也就是说b到d的距离为x步,可以发现,在相遇点,让慢指针回到起点走x步,让快指针从相遇点c走x步(两者都每次走一步,因为b到d的距离为x, 而b到c的距离为y, d到b的距离为y, 相当于将起点往后移动了y步,则从c点出发走x步能到达b),则二者会相遇在环入口b处,此时返回任一指针指代的节点即可。
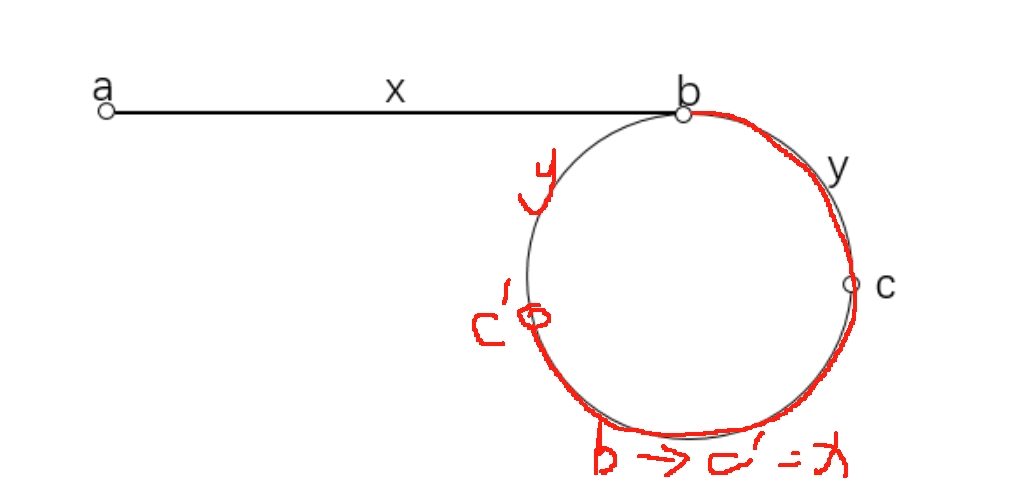

时间复杂度:O(n)
注释代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {if(!head || !head -> next) return NULL;auto s = head, f = head -> next;while(f){s = s -> next, f = f -> next;if(!f) return NULL;f = f -> next;if(s == f) //找到相遇点,让慢指针从头开始走,而快指针则从相遇点开始走{s = head, f = f -> next; //处理边界问题,因为初始化时s = head , f= head -> next ,因此这里的f应该也要往后移一位,保持原状while(s != f) s = s -> next, f = f -> next; //将两个指针分别移动,直到二者相遇return s; //相遇的点就是入口点}}return NULL;}
};
纯享版:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {if(!head || !head -> next) return NULL;auto s = head, f = head -> next;while(f){s = s -> next, f = f -> next;if(!f) return NULL;f = f -> next;if(s == f){s = head, f = f -> next;while(s != f) s = s -> next, f = f -> next;return s;}}return NULL;}
};LeetCode143.重排链表:
题目描述:
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
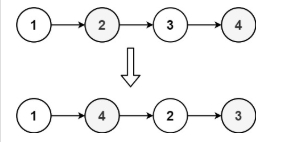
输入:head = [1,2,3,4]
输出:[1,4,2,3]
示例 2:
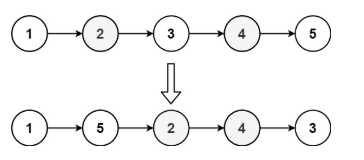
输入:head = [1,2,3,4,5]
输出:[1,5,2,4,3]
提示:
链表的长度范围为 [1, 5 * 10^4]
1 <= node.val <= 1000
思路:
先统计链表长度n,通过(n+1)/2下取整找到链表中点,将中点后面的一段链表进行翻转,再使用p和q两个指针分别从头尾开始往中间靠,来重新组装链表,最后通过判断链表的奇偶将mid或者mid后一位(也就是后半段的最后一个)指向空,当作尾节点。
细节:
1.编程中一般是下取整比如n/2=4,当长度为奇数时,想要取中点需要(n + 1) / 2
2.链表移动通常从头节点开始,需要找到中间节点的话,只要移动(n + 1) / 2 - 1步即可
时间复杂度:

注释代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:void reorderList(ListNode* head) {if(!head) return;int n = 0;for(auto p = head; p; p = p -> next) n++; //记录整个链表长度auto mid = head;//正常来说将长度为n的链表平均分为两段是n / 2的,但是如果是奇数的话n/2是下取整,比如n=9取到的是第4个节点//并不是我们想要的,所以(n + 1) / 2 进行下取整的话就刚好是第5个点//同时这里为什么要减1,因为mid从头节点开始,只需要跳四次就能到达第五个点for(int i = 0; i < (n + 1) / 2 - 1; i++) mid = mid -> next; //找到中间的节点auto a = mid, b = a -> next; for(int i = 0; i < n / 2; i++) //将后半段翻转过来{auto c = b -> next;b -> next = a;a = b, b = c;}auto p = head, q = a; //p从头开始,q从尾开始for(int i = 0; i < n / 2; i++) //两头交叉组装{auto o = q -> next; //保持q的下一个节点指向q -> next = p -> next;p -> next = q; p = q -> next; //p跳到连接q的后面节点q = o; //q重新赋值成原本节点}if(n % 2) mid -> next = NULL; //如果是奇数的话,中间节点就是尾节点else mid -> next -> next = NULL; //偶数的话,}
};纯享版:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:void reorderList(ListNode* head) {if(!head) return;int n = 0;for(auto p = head; p; p = p -> next) n++;auto mid = head;for(int i = 0; i < (n + 1) / 2 - 1; i++) mid = mid -> next;auto a = mid, b = a -> next;for(int i = 0; i < n / 2; i++){auto c = b -> next;b -> next = a;a = b, b = c;}auto p = head, q = a;for(int i = 0; i < n / 2; i++){auto o = q -> next;q -> next = p -> next;p -> next = q;p = q -> next;q = o;}if(n % 2) mid -> next = NULL;else mid -> next -> next = NULL;}
};LeetCode144.二叉树的前序遍历:
题目 描述:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
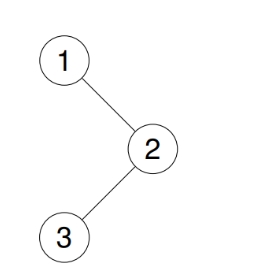
输入:root = [1,null,2,3]
输出:[1,2,3]
解释:
示例 2:
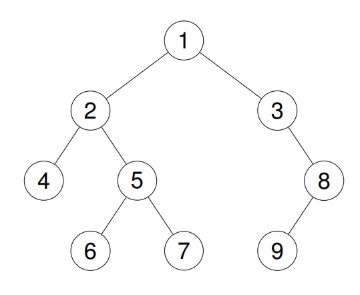
输入:root = [1,2,3,4,5,null,8,null,null,6,7,9]
输出:[1,2,4,5,6,7,3,8,9]
解释:
示例 3:
输入:root = []
输出:[]
示例 4:
输入:root = [1]
输出:[1]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶:递归算法很简单,你可以通过迭代算法完成吗?
做法1:(递归做法)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;vector<int> preorderTraversal(TreeNode* root) {dfs(root);return res;}void dfs(TreeNode* root){if(!root) return;res.push_back(root -> val);dfs(root -> left);dfs(root -> right);}
};做法2:(迭代做法)
思路:
跟中序遍历是一致的,先将左链全部加入栈中,每次将栈顶的节点取出来遍历它的右子树,同时去除该节点
时间复杂度:每个节点遍历一次,总的时间复杂度为O(n)
注释代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int> res;stack<TreeNode*> stk;while(root || stk.size()){while(root){res.push_back(root -> val);stk.push(root);root = root -> left;}root = stk.top();stk.pop();root = root -> right;}return res;}
};
LeetCode145.二叉树的后序遍历:
题目描述:
做法1:(递归做法)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;vector<int> postorderTraversal(TreeNode* root) {dfs(root);return res;}void dfs(TreeNode* root){if(!root) return;dfs(root -> left);dfs(root -> right);res.push_back(root -> val);}
};做法2:(迭代做法):
思路:
其实二叉树的前、中、后三种遍历无非就是看根的遍历顺序,先遍历根那就是前序遍历,根在中间遍历就是中序遍历, 最后遍历根就是后序遍历
二叉树的三种遍历:
1.前序遍历: 根 左 右
2.中序遍历: 左 根 右
3.后序遍历: 左 右 根
对比二叉树的前后遍历会发现: 我们按照前序遍历的样式先对二叉树进行 根 右 左的顺序先遍历最后再将答案翻转一下就是 左 右 根 -》也就是后序遍历了
时间复杂度:O(n)
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> postorderTraversal(TreeNode* root) {vector<int> res;stack<TreeNode*> stk;while(root || stk.size()){while(root){res.push_back(root -> val);stk.push(root);root = root -> right;}root = stk.top();stk.pop();root = root -> left;}reverse(res.begin(), res.end());return res;}
};LeetCode146.LRU缓存机制:
题目描述:
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 10^5
最多调用 2 * 10^5 次 get 和 put
思路:
首先涉及到查找关键字肯定使用hash表查询是O(1)的,同时这里需要按照最近最少使用来更新状态,我们可以使用一个数字来表示先后,但考虑的细节太多,于是考虑到我们每次将查询或者放入的值更新到最前面,那么留在最后面的就是最近最少使用的,这里使用双链表最为合适,每get或者put一次,就将该节点放到最左侧(或者最右侧),这样如果put时超出容量就将最右侧(或者最左侧)的节点删除
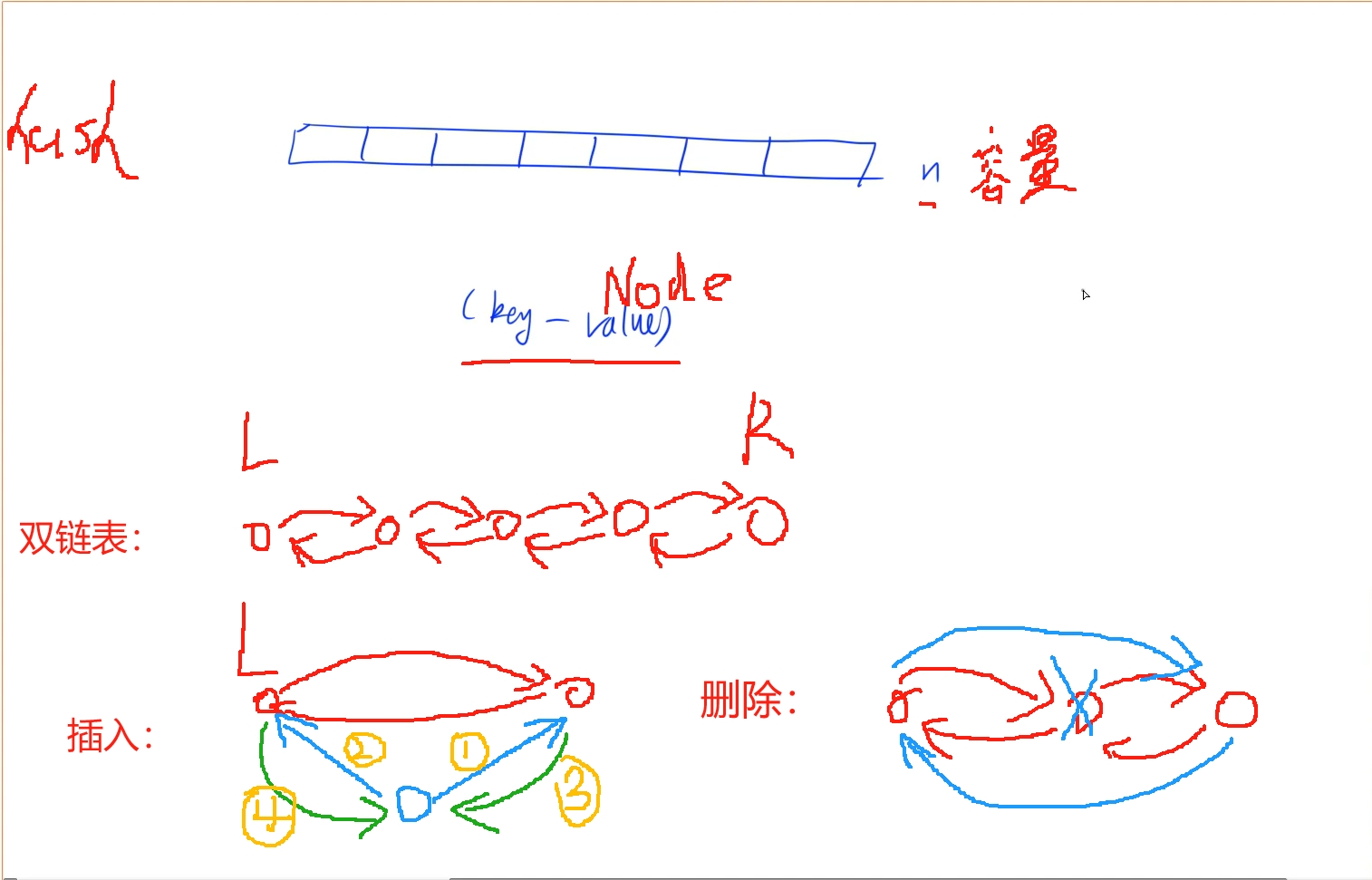
时间复杂度:

注释代码:(超出容量时删除最右侧)
class LRUCache {
public:struct Node{ //定义双链表的节点构造int key, val;Node *left, *right;Node(int _key, int _val): key(_key), val(_val), left(NULL), right(NULL){}}*L, *R;unordered_map<int, Node*> hash; //hash表存的是节点和关键字,这样通过关键字在O(1)的时间就能找到对应节点int n;void remove(Node* p) //删除一个节点{p -> left -> right = p -> right;p -> right -> left = p -> left;}void insert(Node* p) //将一个节点插在最左侧点后面{p -> right = L -> right;L -> right -> left = p;p -> left = L;L -> right = p;}LRUCache(int capacity) {n = capacity;L = new Node(-1, -1), R = new Node(-1, -1); //定义双链表头尾两个节点L -> right = R, R -> left = L; //建立双向指向}int get(int key) {if(hash.count(key) == 0) return -1;auto p = hash[key]; //找到这个点,并将它挪到最左侧remove(p);insert(p);return p -> val;}void put(int key, int value) {if(hash.count(key)) //存在这个点则找到该点,并将值修改为新的值,同时从双链表中取出并放在最左侧{auto p = hash[key];p -> val = value;remove(p);insert(p);}else{ //不存在则创建该节点并放在双链表的最左侧if(hash.size() == n){auto p = R -> left; //删掉最右侧点的左侧的节点remove(p);hash.erase(p -> key);delete p;}auto p = new Node(key, value);hash[key] = p;insert(p);}}
};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/纯享版:(超出容量时删除最左侧)
class LRUCache {
public:struct Node{int key, val;Node *left, *right;Node(int _key, int _val): key(_key), val(_val), left(NULL), right(NULL){}}*L, *R;unordered_map<int, Node*> hash;int n;void remove(Node* p){p -> left -> right = p -> right;p -> right -> left = p -> left;}void insert(Node* p){p -> right = R;R -> left -> right = p;p -> left = R -> left;R -> left = p;}LRUCache(int capacity) {n = capacity;L = new Node(-1, -1), R = new Node(-1, -1);L -> right = R, R -> left = L;}int get(int key) {if(hash.count(key) == 0) return -1;auto p = hash[key];remove(p);insert(p);return p -> val;}void put(int key, int value) {if(hash.count(key)){auto p = hash[key];p -> val = value;remove(p);insert(p);}else{if(hash.size() == n){auto p = L -> right;remove(p);hash.erase(p -> key);}auto p = new Node(key, value);hash[key] = p;insert(p);}}
};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/
LeetCode147.对链表进行插入排序:
题目描述:
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。
示例 1:
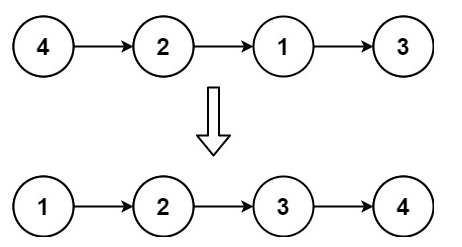
输入: head = [4,2,1,3]
输出: [1,2,3,4]
示例 2:
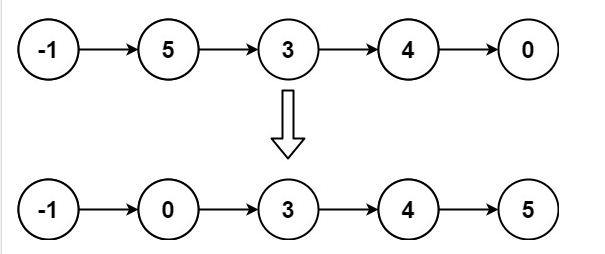
输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
提示:
列表中的节点数在 [1, 5000]范围内
-5000 <= Node.val <= 5000
思路:
从前往后遍历链表的每一个节点,每次找到第一个比当前节点值大的节点,将当前节点插入到该节点前面
时间复杂度:
注释代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* insertionSortList(ListNode* head) {auto dummy = new ListNode(-1);for(auto p = head; p; ){auto cur = dummy, next = p -> next; //要将当前遍历到的节点的下一位存储下来while(cur -> next && cur -> next -> val <= p -> val) cur = cur -> next; //找到第一个比当前节点大的节点p -> next = cur -> next; //当前节点肯定是在p节点后面的,所以p的next是当前节点的nextcur -> next = p; //当前节点的下一位为pp = next;}return dummy -> next;}
};纯享版:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* insertionSortList(ListNode* head) {auto dummy = new ListNode(-1);for(auto p = head; p;){auto cur = dummy, next = p -> next;while(cur -> next && cur -> next -> val <= p -> val) cur = cur -> next;p -> next = cur -> next;cur -> next = p;p = next;}return dummy -> next;}
};
LeetCode148.排序链表:
#题目描述:
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
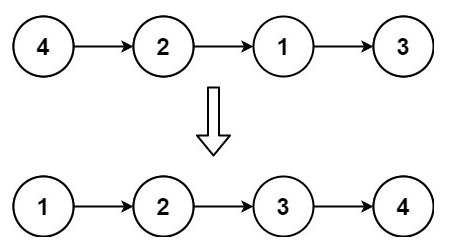
输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
提示:
链表中节点的数目在范围 [0, 5 * 10^4] 内
-10^5 <= Node.val <= 10^5
进阶:你可以在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
思路:
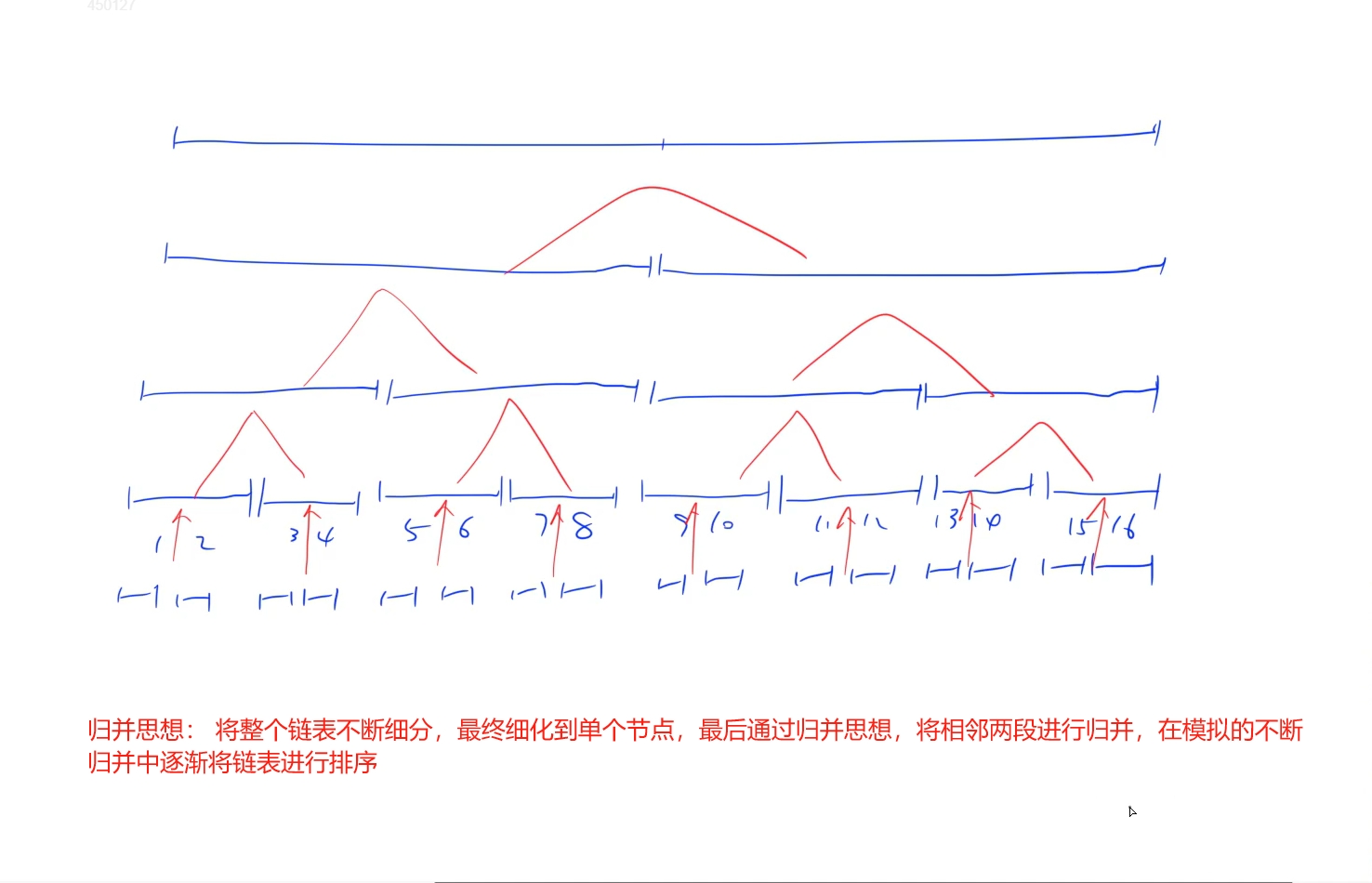
时间复杂度:

注释代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* sortList(ListNode* head) {int n = 0;for(auto p = head; p; p = p -> next) n++;//注意:这里的i和j仅仅是维护每段的节点个数和合并的次数, 链表中的每段起点是由p、q、 o维护for(int i = 1; i < n; i *= 2) //每次需要合并的小段的链表长度{auto dummy = new ListNode(-1), cur = dummy;for(int j = 1; j <= n; j += i * 2) //对于该长度下的小段一共需要合并几次{auto p = head, q = p; //p为前一段的开头for(int k = 0; k < i && q; k++) q = q -> next; //q为后一段的开头auto o = q;for(int k = 0; k < i && o; k++) o = o -> next; //o为下段合并的起点int l = 0, r = 0;while(l < i && r < i && p && q) //前后两段都不能超过i的长度,并且p和q必须存在{//将值小的放入cur之后,并且对应的长度计数加1if(p -> val < q -> val) cur = cur -> next = p, p = p -> next, l++;else cur = cur -> next = q, q = q -> next, r++; }while(l < i && p) cur = cur -> next = p, p = p -> next, l++; //将该段剩余节点插入链表尾部while(r < i && q) cur = cur -> next = q, q = q -> next, r++;head = o; //跳到下段合并的起点}cur -> next = NULL; //将合并后的段尾连向空head = dummy -> next; //将head连接上虚拟头节点}return head;}
};纯享版:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* sortList(ListNode* head) {int n= 0;for(auto p = head; p; p = p -> next) n++;for(int i = 1; i < n; i *= 2){auto dummy = new ListNode(-1), cur = dummy;for(int j = 1; j <= n; j += i * 2){auto p = head, q = p;for(int k = 0; k < i && q; k++) q = q -> next;auto o = q;for(int k = 0; k < i && o; k++) o = o -> next;int l = 0, r = 0;while(l < i && r < i && p && q){if(p -> val <= q -> val) cur = cur -> next = p, p = p -> next, l++;else cur = cur -> next = q, q = q -> next, r++;}while(l < i && p) cur = cur -> next = p, p = p -> next, l++;while(r < i && q) cur = cur -> next = q, q = q -> next, r++;head = o;}cur -> next = NULL;head = dummy -> next;}return head;}
};LeetCode149.直线上最多的点数:
题目描述:
给你一个数组 points ,其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点。求最多有多少个点在同一条直线上。
示例 1:
输入:points = [[1,1],[2,2],[3,3]]
输出:3
示例 2:
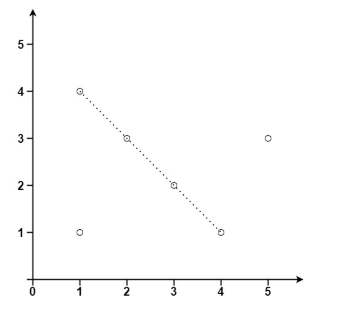
输入:points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出:4
提示:
1 <= points.length <= 300
points[i].length == 2
-10^4 <= xi, yi <= 10^4
points 中的所有点 互不相同
思路:
使用哈希表记录每两个点之间的斜率,斜率相同的直线数量即是
时间复杂度:

注释代码:
class Solution {
public:int maxPoints(vector<vector<int>>& points) {typedef long double LD;int res = 0;for(auto& p : points){int ss = 0, vs = 0; //ss相同的点,vs斜率为0的点unordered_map<LD, int> cnt;for(auto& q : points){if(p == q) ss++; //如果两个点值一样的话,点数加1else if(p[0] == q[0]) vs++; //横坐标相同, 说明在同一条垂线上else{LD k = (LD)(q[1] - p[1]) / (q[0] - p[0]); //计算每两个点之间的斜率cnt[k]++; //记录斜率相同的次数}}int c = vs; //先接下位于同一条垂线上的点数for(auto [k, t]: cnt) c = max(c, t); //斜率相同的个数就是在同一条直线上的点的个数res = max(res, c + ss); //同时加上点本身或者跟本点系统的个数}return res;}
};
纯享版:
class Solution {
public:int maxPoints(vector<vector<int>>& points) {typedef long double LD;int res = 0;for(auto& p : points){unordered_map<LD, int> cnt;int vs = 0, ss = 0;for(auto& q : points){if(p == q) ss = 1;else if(p[0] == q[0]) vs++;else{LD k = (LD)(q[1] - p[1]) / (q[0] - p[0]);cnt[k]++;}}int c = vs;for(auto [k, t]: cnt) c = max(c, t);res = max(res, c + ss); }return res;}
};
LeetCode150.逆波兰表达式求值:
题目描述:
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = [“2”,“1”,“+”,“3”,“*”]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = [“4”,“13”,“5”,“/”,“+”]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 10^4
tokens[i] 是一个算符(“+”、“-”、“*” 或 “/”),或是在范围 [-200, 200] 内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
思路:
逆波兰表达式就是利用栈依次存储每个数字,每次遇到运算符就对栈顶的两个元素进行运算
时间复杂度:
每个元素最多进栈一次出栈一次,总的时间复杂度是O(n)的
注释代码:
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> stk;int res = 0;for(auto& s : tokens){if(s == "*" || s == "/" || s == "+" || s == "-") //如果是运算符,则将栈顶两个元素进行运算{auto b = stk.top(); stk.pop();auto a = stk.top(); stk.pop();if(s == "+") a = a + b;else if(s == "-") a -= b;else if(s == "*") a *= b;else a /= b;stk.push(a); //计算结果塞回栈顶}else{stk.push(stoi(s)); //如果是数字则将字符转成int塞入栈顶}}return res = stk.top(); //栈顶就是最后结果}
};纯享版:
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> stk;int res = 0;for(auto& s : tokens){if(s == "*" || s == "/" || s == "-" || s == "+"){int b = stk.top(); stk.pop();int a = stk.top(); stk.pop();if(s == "*") a *= b;else if(s == "-") a -= b;else if(s == "+") a += b;else a /= b;stk.push(a);}else{stk.push(stoi(s));}}return res = stk.top();}
};