四边形(梯形、平行四边形、矩形、菱形和正方形)
四边形是一种二维图形,其特征是具有四条边、四个顶点和四个角。它大致可分为两类:凹四边形和凸四边形。凸四边形又包括几种具体类型的四边形,包括梯形、平行四边形、矩形、菱形和正方形。
四边形的内角和为360°。让我们详细了解什么是四边形,它的形状、类型、性质、公式和示例。
什么是四边形?
四边形定义为具有四个角的四边形,四边形是一种边以适当模式定义的多边形。
四边形是一种具有四条边、四个角和四个角的形状。无论四边形是什么类型,其所有内角之和始终等于 360 度。四边形有多种形式,每种形式都有其独特的属性,这些属性决定了它们的角度、边和对称性。四边形的例子包括正方形、长方形、平行四边形、菱形、梯形和风筝形。每种类型都有其独特的特征和属性,但它们都是四边形。
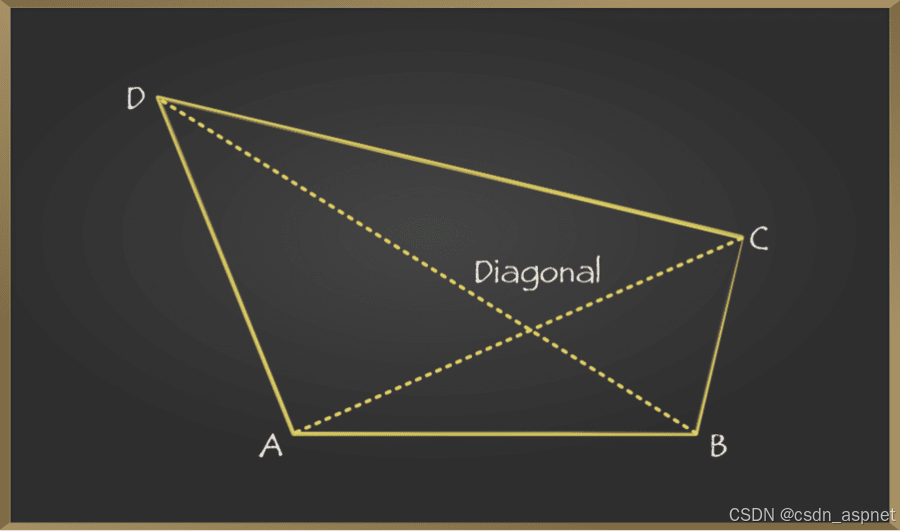
例如,在上图中,四边形定义为ABCD、ADCB、BCDA、CDAB等,但不能定义为ACBD或BDAC。此处,四边形的边为AB、BC、CD和DA,对角线为AC和BD。
四边形的性质
四边形的性质有:
- 它有 4 条边( AB、BC、CD 和 DA)。
- 它有 4 个顶点(A、B、C、D)。
- 它有4个角。(∠A、∠B、∠C、∠D)。
- 它有两条对角线。(AC 和 BD)
- 其内角和为360°。(∠A + ∠B + ∠C + ∠D = 360°)。
- 它的外角和为360°。
凸四边形和凹四边形
根据四边形的性质,四边形可分为两大类:
- 凸四边形和
- 凹四边形。
这些凹四边形和凸四边形可以进一步细分。
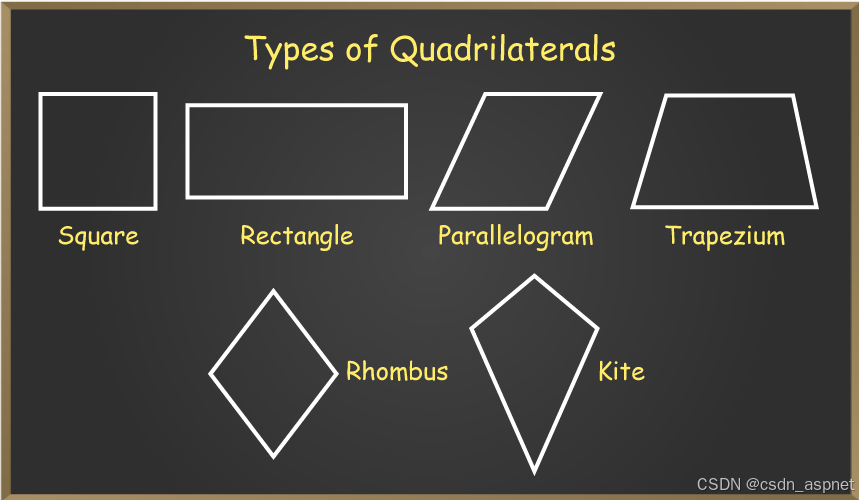
不同四边形的形状
凹四边形
有一个内角大于180°,且有一条对角线位于四边形外部的四边形称为凹四边形。
凹四边形的一个例子是飞镖。它是一种像风筝一样具有双侧对称性的四边形,但具有一个反射内角。
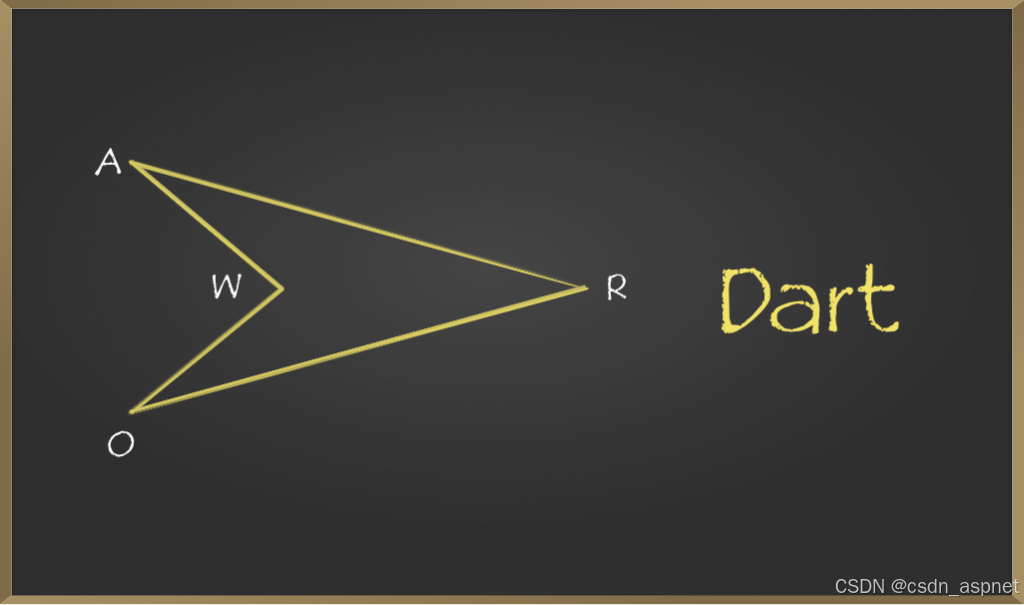
飞镖示意图
如下图所示,四边形的一个内角为 210°,大于 180°。因此,该四边形为凹四边形。
凹四边形
四个内角均小于180°的四边形称为凹四边形。
凹四边形有多种类型,包括:
- 梯形
- 风筝
- 平行四边形
- 长方形
- 菱形
- 正方形
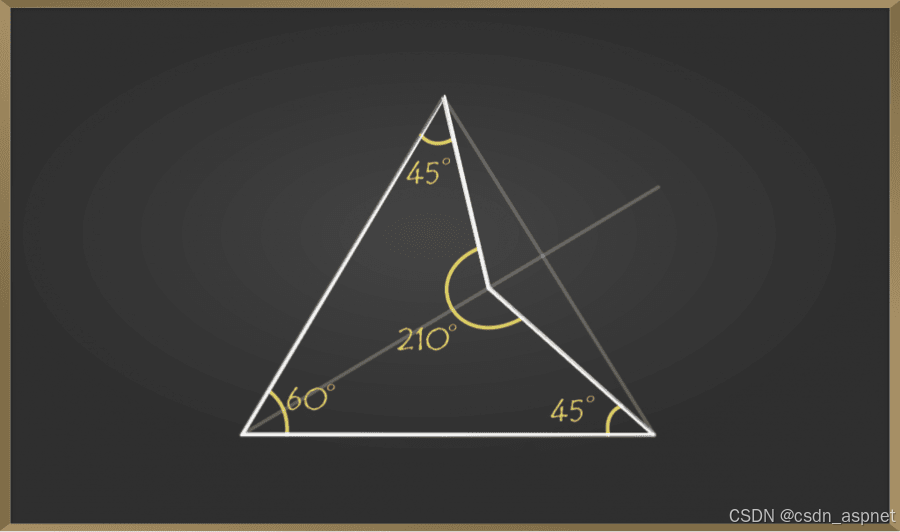
凸四边形
常见的四边形类型
四边形的形状多种多样,从对称的正方形和长方形到更复杂和不规则的平行四边形和梯形。
正方形
所有边相等、对边平行且所有内角都等于90°的四边形,称为正方形对角线互相垂直的四边形。注意,所有正方形都是菱形,但反之则不然。
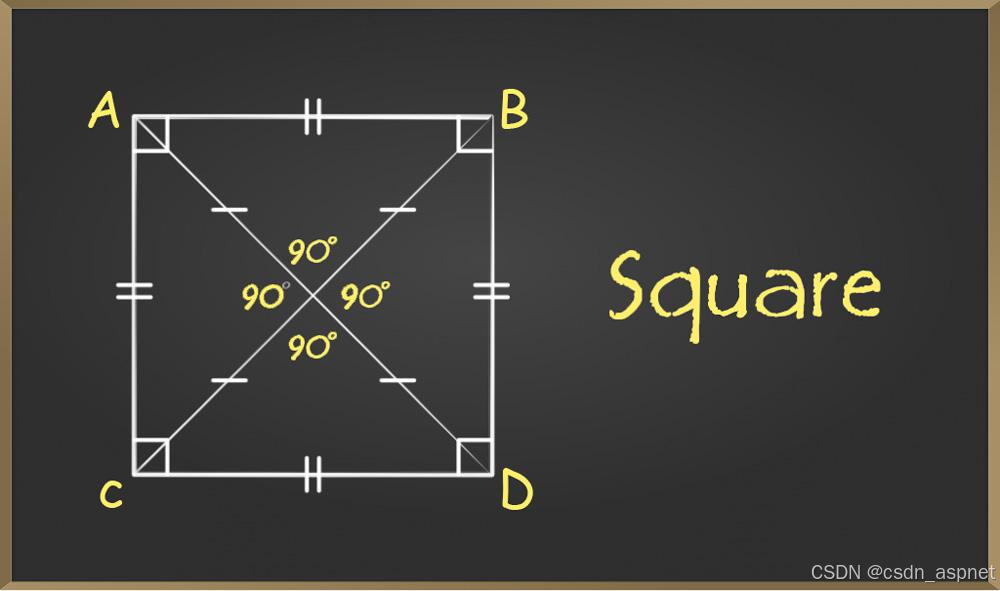
Square 的属性
正方形的属性是:
- 正方形的四条边都相等。
- 正方形的内角为90°。
- 正方形的对角线以 90° 角平分。
- 正方形的对边平行,邻边垂直。
| 平方公式 | |
|---|---|
| 正方形面积 | side2(一个边长平方) |
| 正方形周长 | 4 × side(4x一个边长) |
其中 side 是任意一条边的长度。
长方形
矩形是对边相等且平行且所有内角都等于 90° 的四边形。
矩形的对角线互相平分。
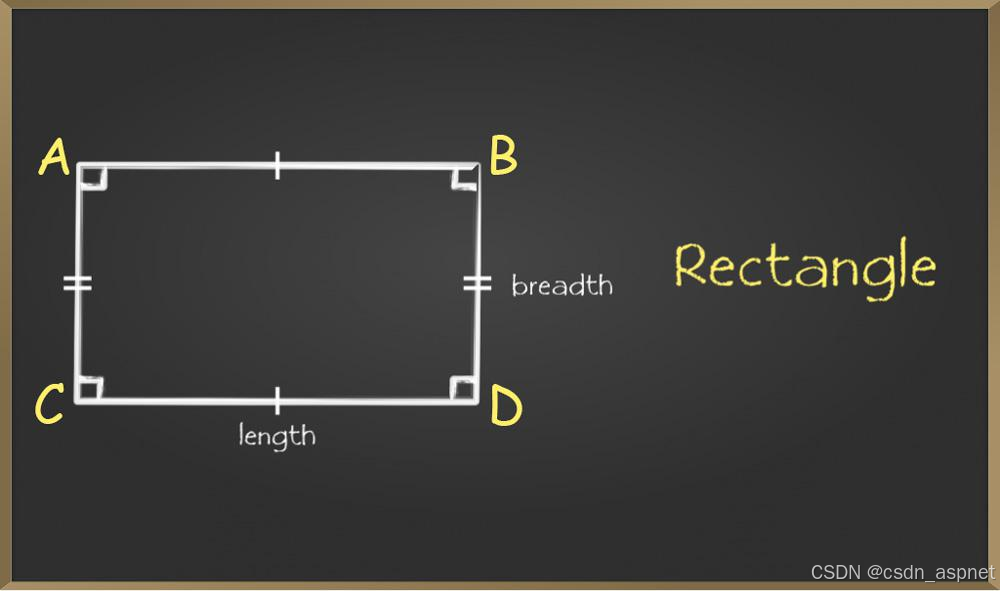
矩形插图
请注意,所有矩形都是平行四边形,但反之则不然。
矩形属性
以下是矩形的一些重要属性:
- 矩形的对边平行且相等。上例中,AB与CD平行且相等,AC与BD平行且相等。
- 矩形的4个角都相等,且都等于90°。∠A = ∠B = ∠C = ∠D = 90°。
- 矩形的对角线互相平分,且矩形的对角线相等,此时 AD = BC。
| 矩形公式 | |
|---|---|
| 矩形面积 | 长×宽 |
| 矩形的周长 | 2 × (长+宽) |
菱形
菱形是一种四边形,其所有边都相等,对边平行。菱形的对角相等,对角线互相垂直平分。
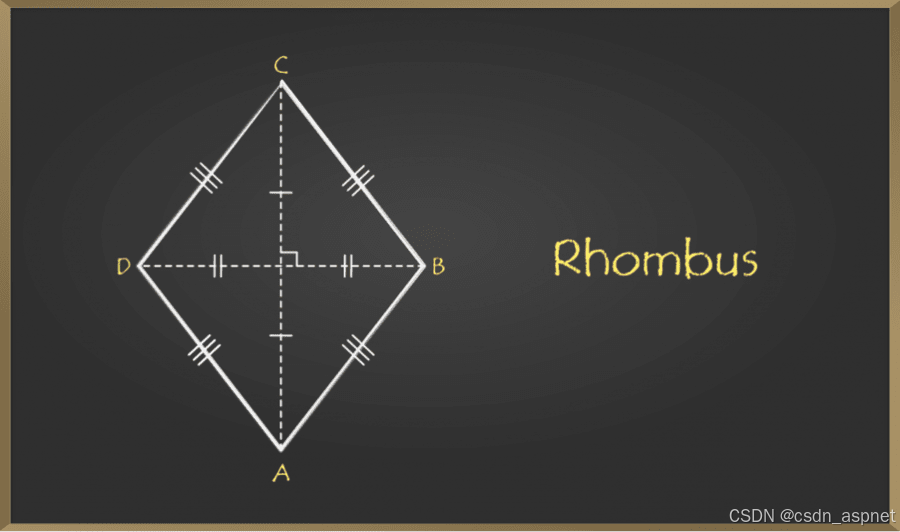
菱形图
请注意,所有菱形都是平行四边形,但反之则不然。
菱形的性质
以下是菱形的一些主要属性:
- 菱形的四条边相等。AB = BC = CD = AD。
- 菱形的对边平行且相等。上图中,AB平行于CD,AD平行于BC。
- 菱形的对角线以 90° 相互平分。
| 菱形公式 | |
|---|---|
| 菱形的面积 | 1/2×(对角线1×对角线2) |
| 菱形的周长 | 4 × side |
其中 side 是任意一条边的长度。
平行四边形
平行四边形是对边相等且平行的四边形。平行四边形的对角相等,对角线互相平分。
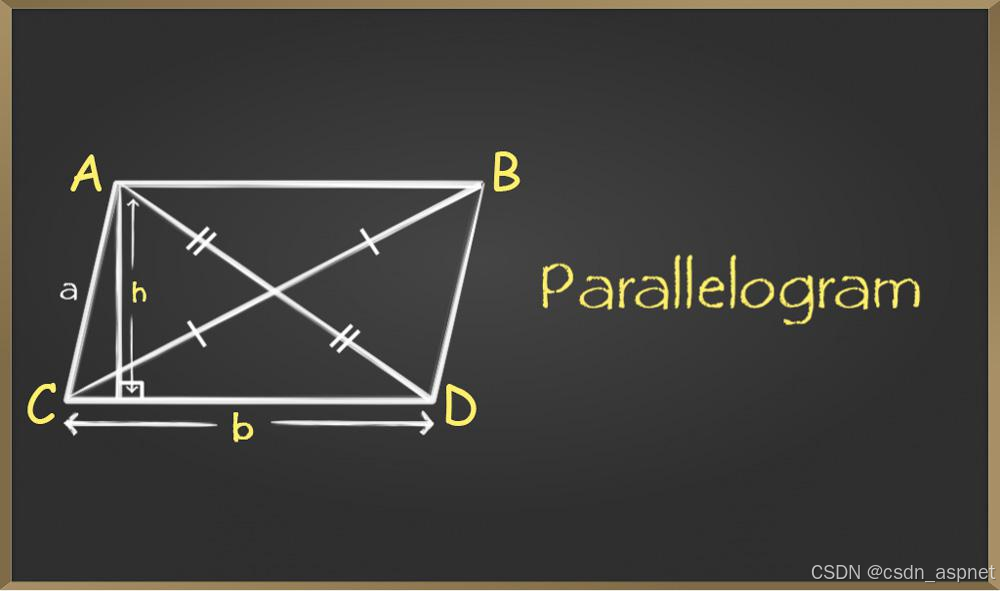
平行四边形插图
平行四边形的性质
平行四边形的属性是:
- 平行四边形的对边平行且相等。上例中,AB与CD平行且相等,AC与BD平行且相等。
- 平行四边形的对角相等。∠A = ∠D 且 ∠B = ∠C。
- 平行四边形的对角线互相平分。
| 平行四边形公式 | |
|---|---|
| 平行四边形的面积 | 底×高 |
| 平行四边形的周长 | 2 × (a+b) |
其中,a、b为平行四边形的邻边。
梯形
梯形是一对对边平行的四边形。正梯形的非平行边相等,且底角也相等。
梯形的面积=1/2×平行边之和×平行边之间的距离。
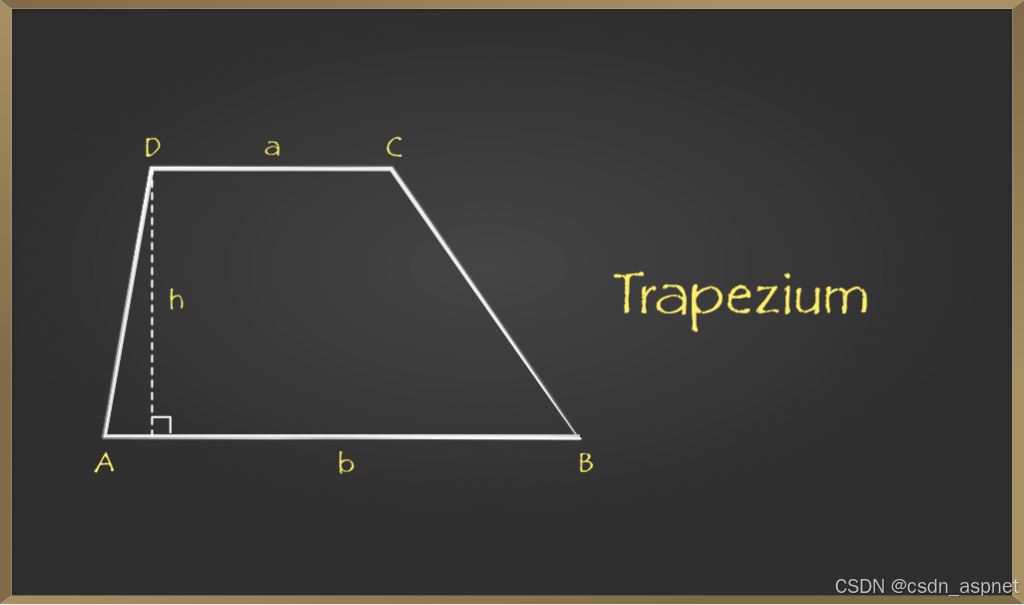
梯形图
梯形的性质
以下是梯形的两个重要属性:
- 梯形中相互平行的边称为梯形底。上图中,AB 和 CD 是梯形的底。
- 梯形中不平行的边称为梯形腿。上图中,AD和BC就是梯形腿。
| 梯形公式 | |
|---|---|
| 梯形面积 | 1/2 ×(a+b)×(h) |
| 梯形的周长 | a+b+c+d |
其中 a、b、c、d 是梯形的边,(a和b)是平行边,高度(h)是这些平行边之间的垂直距离。
风筝
风筝有两对邻边相等,有一对对角相等。风筝的对角线垂直相交。
风筝最长的对角线将较小的对角线一分为二。
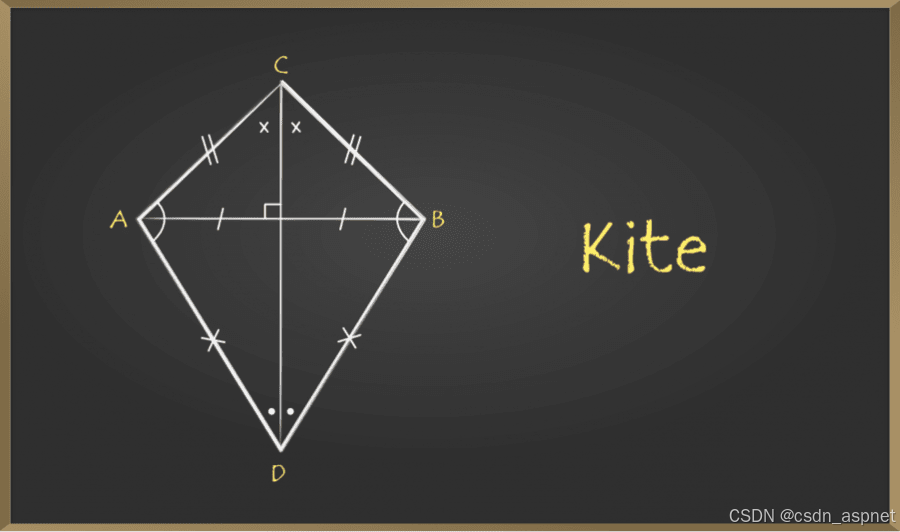
风筝插图
风筝的属性
让我们讨论一下风筝的一些特性。
- 风筝形有两对相等的相邻边。例如,AC = BC,AD = BD。
- 钝角的内对角相等;这里,∠A = ∠B。
- 风筝的对角线彼此垂直;这里,AB 垂直于 CD。
- 风筝线较长的对角线平分较短的对角线。这里,CD 平分 AB。
| 风筝公式 | |
|---|---|
| 风筝面积 | ½(对角线1 x 对角线2) |
| 风筝的周长 | 2(a + b) |
其中,a 和 b代表 风筝两对相等边 的长度 。
四边形定理
- 内角和定理:任何四边形的内角和都等于 360 度。
- 对角定理:在四边形中,两个对角的度数之和为 180 度。
- 连续角定理:四边形中相邻(连续)角互补,即它们的角和为 180 度。
- 平行四边形对角线定理:平行四边形的对角线互相平分,将每条对角线分成两个相等的部分。
- 平行四边形的对边和对角定理:在平行四边形中,对边长度相等,对角全等。
- 矩形和菱形的对角线定理:矩形和菱形的对角线相等。此外,矩形的对角线全等,而菱形的对角线互相垂直平分。
- 梯形对角线定理:梯形的对角线长度可能不尽相同。然而,连接非平行边中点的线段与底边平行,且等于底边和的一半。
四边形对称线
四边形有对称线,对称线是穿过四边形中心并将其分成两个相似部分的假想线。对称线可以:
- 将线一侧的两个顶点与另一侧的两个顶点匹配。
- 穿过两个顶点,当沿线折叠时,另外两个顶点配对。
正四边形有四条对称线。例如,正方形有四条对称线,包括对角线和连接对边中点的线。矩形有两条对称线,包括连接对边和平行线中点的线。
四边形的边和角
下表说明了四边形的边和角如何使它们彼此不同:
| 四边形的特征 | |||||
|---|---|---|---|---|---|
| 边和角 | 正方形 | 长方形 | 菱形 | 平行四边形 | 梯形/梯形 |
| 各方平等 | 是的 | 不 | 是的 | 不 | 不 |
| 对边平行 | 是的 | 是的 | 是的 | 是的 | 是(只有一对对边是平行线) |
| 对边相等 | 是的 | 是的 | 是的 | 是的 | 不 |
| 所有角度都相同 | 是 (90°) | 是 (90°) | 不 | 不 | 不 |
| 对角相等 | 是的 | 是的 | 是的 | 是的 | 不 |
| 对角线互相平分 | 是的 | 是的 | 是的 | 是的 | 不 |
| 两个相邻角互补 | 是的 | 是的 | 是的 | 是的 | 是(只有非平行边上的相邻角才是互补的) |
| 对称线 | 4 | 2 | 2 | 0 | 0 |
四边形解题示例
这里有一些关于四边形的解答例子,希望能对您有所帮助。
问题 1:四边形 ABCD 的周长为 46 个单位。AB = x + 7,BC = 2x + 3,CD = 3x - 8,DA = 4x - 6。求四边形最短边的长度。
解决方案:
周长 = 所有边之和
= 46 = 10x - 4 或 [x = 5]
得出 AB = 12 个单位,BC = 13 个单位,CD = 7 个单位,DC = 14 个单位
因此,最短边的长度为 7 个单位(即 CD)。
问题 2:给定一个梯形 ABCD (AB || DC),其中线为 EF。AB = 3x - 5,CD = 2x -1 且 EF = 2x + 1。求 EF 的值。
解决方案:
我们知道梯形的中线是其底边和的一半。
= EF = (AB + CD) / 2
= 4x + 2 = 5x - 6 或 [x = 8]
因此 EF = 2x + 1 = 2(8) + 1 => EF = 17 个单位。
问题 3:平行四边形的邻角比为 1:2。求该平行四边形所有角的度数。
解决方案:
令邻角为x和2x。
我们知道平行四边形的邻角互补。
= x + 2x = 180° 或 [x = 60°]
此外,平行四边形中的对角相等。
因此每个角度的度数为60°、120°、60°、120°。
| 与四边形相关的文章 | |
|---|---|
| 多边形的类型 https://blog.csdn.net/hefeng_aspnet/article/details/149325305 | 四边形的面积 https://blog.csdn.net/hefeng_aspnet/article/details/149325782 |
| 四边形的构造 https://blog.csdn.net/hefeng_aspnet/article/details/149326004 | 圆内接四边形的面积 https://blog.csdn.net/hefeng_aspnet/article/details/149326064 |
结论
四边形是一种二维形状,具有四条边、四个角和四个角,内角和为 360 度。主要有两种类型:凹四边形(至少有一个角大于 180 度)和凸四边形(所有角均小于 180 度)。凸四边形包括梯形、平行四边形、矩形、菱形、正方形和风筝形。每种类型都有其独特的性质以及面积和周长的计算公式。例如,矩形的面积是长乘以宽,而菱形的面积是其对角线乘积的一半。这些形状的对称性和诸如边长相等或直角相等的性质各不相同,这使得它们在建筑和设计等领域都有不同的应用。
参考:Quadrilaterals - GeeksforGeeks
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。
