频域中的正弦波
频域中的正弦波:
在射频或通信系统中,经常会提到频域这个词。在高速数字应用中也会遇到频域,每位工程师都会多次听到并用到这个术语。然而,当提到频域时,它究竟意味着什么?频域是什么?是什么使得它这么特别又这么好用?
提示 : 频域最重要的性质是:它不是真实的,而是一个数学构造。时域是唯一客观存在的域,而频域是一个遵循特定规则的数学世界。
正弦波是频域中唯一存在的波形,这是频域中最重要的法则,即正弦波是频域的语言。
还有一些其他的域,使用的是其他特殊函数。如JPEG图像压缩算法采用的特殊波形为小波。小波变换是对包含了许多x-y幅值信息的空域进行变换,把它转化为不同的数学描述。这样就能用不到10%的存储空间描述同样的信息。这是一种近似,但却非常有用。
工程师们通常选择在频域中使用正弦波,是因为时域中的任何波形都可用正弦波合成。
这是 正弦波的一个非常重要的性质,然而,它并不是正弦波的独有特性,还有许多其他的波形也有这样的性质。
事实上,正弦波有如下4个性质,使其能够很有效地描述其他任一波形:
1.时域中的任何波形都可由正弦波的组合完全且唯一地描述。
2.任何两个频率不同的正弦波都是正交的。如果将两个正弦波相乘并在整个时间轴上求积分,则积分值为零
3.正弦波有完美的数学定义。
4.正弦波及其微分值处处存在,没有上下边界。现实世界是无穷的,因此可用正弦波描述现实中的波形
这几条性质都是至关重要的,但并不是正弦波独有的。有一类函数集合称为标准正交函数,有时也称为本征函数或基函数,这类函数可用于描述任何时域波形。除正弦波以外的其他标准正交函数有:埃尔米特多项式、勒让德多项式、拉格朗日多项式和贝塞尔函数
为什么选择正弦波作为频域中的函数形式呢?它有什么特别之处?问题的关键在于,如果使用正弦波,与互连的电气效应相关的一些问题就会变得更容易理解和解决。如果变换到频域并使用正弦波描述,有时就会比仅在时域中能更快地得到答案。
提示 :毕竟,时域是客观存在的,我们不能脱离这个基础,除非频域中有求解答案的捷径。
对于信号完整性中经常遇到的各种类型的电气问题,有时利用正弦波能够更快地得到满意的答案。
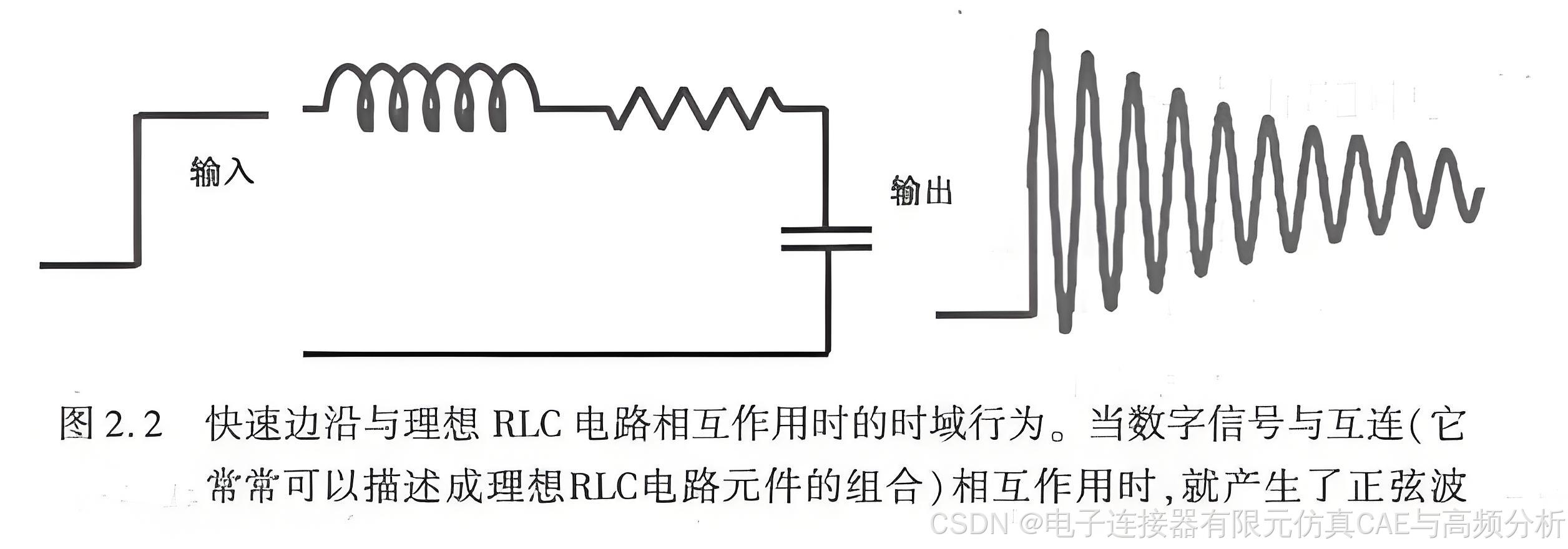
看看表征互连的电路,会发现这些电路常常包括电阻器、电感器和电容器的组合。电路中的这些元件可以用二阶线性微分方程描述,而这类微分方程的解就是正弦波。在这类电路中,实际上产生的波形就是由上述微分方程解所对应的波形组合而成的。
在实际中,首先建立包含R、L和C的电路,并输入任意波形。很多情况下,会得到类似正弦波的波形,而且,用几个正弦波的组合就能很容易的描述这些波形,如图2.2所示。