当前位置：首页 > news >正文

【排序算法】②希尔排序

news 2025/8/10 8:27:04

系列文章目录

第一篇：【排序算法】①直接插入排序-CSDN博客

第二篇：【排序算法】②希尔排序-CSDN博客

第三篇：【排序算法】③直接选择排序-CSDN博客

第四篇：【排序算法】④堆排序-CSDN博客

目录

系列文章目录

前言

一、希尔排序是什么？

算法思想

二、为什么希尔排序能做到排序？

三、实现希尔排序

四、分析希尔排序

总结

前言

所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

为什么我们要学习排序？笔者认为有两点理由：一是面对浩如烟海的各种数据，我们应该学习如何分类、控制这些数据，而排序自然是少不了的；二是人类社会从古至今一直在“排序”，人与人之间，物与物之间，排序涉及到社会的方方面面。

学习并理解排序，不仅有助于工作学习，或许对一些其他方面的理解也会起动到推的效果。

一、希尔排序是什么？

希尔排序法又称缩小增量法，是在直接插入排序的基础上进行优化得来的排序算法。

算法思想

希尔排序法的基本思想是：先选定一个间距整数gap，把待排序文件中所有记录分成gap个组，所有距离为gap的记录分在同一组内，并对每一组内的记录进行直接插入排序。然后，gap--，重复上述分组和排序的工作。当到达gap=1时，所有记录在统一组内排好序。

简单来说，希尔排序分为“预排序”和“正式排序”两步。

二、为什么希尔排序能做到排序？

这里笔者画了草图以帮助大家理解希尔排序：

假设我们排升序，数组为{7 ，1 ，3 ，9 ，6 ，5 ，4 ，8 ，2 ，0}

假设设gap=3：

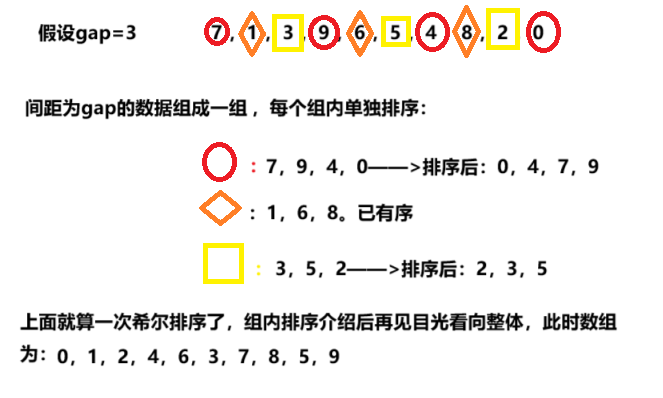
此时将gap-1，在再上一次排序的基础上排：

gap=2，数组为{0，1，2，4，6，3，7，8，5，9}

再将gap-1，此时gap==1，实质上成为直接插入排序。

为什么要分几次预排序，然后还要调用直接插入排序？

还记得插入排序什么时候效率最高吗，当数组接近有序的时候！预排序的过程其实就是让数组接近有序，为后面的gap=1时的插入排序做准备，也就是说希尔排序的最后一步必须是gap==1时的直接插入排序！

三、实现希尔排序

void ShellSort(int* a, int n)
{if (!a)return;int gap = n;//gap>1:确保最后一趟gap==1while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - 1; i += gap){int end = i;int temp = a[end + gap];while (end >= 0&&end+gap<n){//if (temp > a[end])递减if(temp < a[end])//递增{a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = temp;}}
}

代码讲解：

①gap=gap/3，通过将gap/3快速将整个区间划分为多个小区间进行预处理操作。这里除以3是基于前人所做的大量总结中得出的最优解：在效率和计算复杂度间取得平衡。

若gap/2，则递减过慢且中间需要较多次的预排序过程；若gap/>3的数，则递减过快，难以达成预排序的目的：让数组变得尽量有序。

②gap=gap/3+1，这个+1的目的是确保gap永不小于 1，并且使得最后一次循环必定执行gap==1时的直接插入排序。

③for循环中实质为直接插入排序，在上一篇中已经介绍过，若读者有疑惑的地方欢迎在评论区讨论。

四、分析希尔排序

1. 希尔排序是对直接插入排序的优化。

2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。

3.时间复杂度：希尔排序的时间复杂度较难计算，需要用到数学中的概率论证明，这里就省略证明过程，希尔排序的时间复杂度随gap的变化而变化，上述代码中的gap=gap/3+1的时间复杂度为O(N^1.3);

4.空间复杂度为O(1);

5.稳定性分析：不稳定！希尔排序的不稳定性源于它在排序过程中会进行长距离的元素交换，这可能导致相同值的元素在排序后改变相对顺序。

比如：数组{5A, 2, 1 , 5B, 3}（5A和5B是值相同但需区分顺序的两个元素），希尔排序最后结果为{1，2，3，5B，5A}，排序前5A在5B前，排序后5A在5B后！