算法篇----分治（快排）

一、解析

所谓的分治，实际上就是利用排序算法将一个数组排列成按照特定规律的顺序的样子

二、题目解析

1. 颜色分类

75. 颜色分类 - 力扣（LeetCode）

解题思路：

由于这道题只有012三个数字，我们可以找到其中间值，即遍历数组，并将其与1作比较，比1小就扔前面去，比1大就扔到后面去

为了实现上述思路，我们采用“三指针”的算法思想，即确定左右指针left和rright,之后再让变量i遍历数组，这就是三指针~

这里说明一下这三个指针所代表的意义：

left指针：其左侧（包含其本身位置）代表都是一堆0，即已经调整好的左半部分数组

i指针：遍历指针，其右侧（包含本身）为没遍历的数组

right指针：其右侧（包含其本身位置）代表都是一堆2，即已经调整好的右半部分数组

在遍历过程中会遇到如下情况：

1）nums[i] == 0 :比1小，因此要扔到前面去，可以利用swap函数， 即swap[++left,i++],这里是left在交换之前往右走一步，i在交换之后再向右走，而这里之所以可以++，是因为nums[++left]这个数也是被i扫描过的，肯定也是符合比1小的，充其量就是等于1，这种情况下大不了就自己和自己交换呗，没啥影响，但是要是比1大就要注意了~（注意区分1 3点）

2）nums[i] == 1:此时只让i++就好

3）nums[i] == 2:比1大，因此要扔到后面去，可以利用swap函数， 即swap[--right,i],这里right在交换之前向左走一步，但是切记i不要走，因为交换后i这个位置也是未经扫描修改的，换句话说nums[--right]这个数我们还没扫描过，不知道它的大致属性，还需要再次判断，重复上述过程，要是++就会跨过这个数了

class Solution {
public:void sortColors(vector<int>& nums) {int left=-1,right=nums.size(),i=0;while(i<right){if(nums[i]==0) swap(nums[++left],nums[i++]);else if(nums[i]==1) i++;else swap(nums[--right],nums[i]);}}
};

注：这道题非常重要，下面的几道题都是基于此展开的~

2. 排序数组

912. 排序数组 - 力扣（LeetCode）

解题思路：

这道题可以利用快排思想，这里在简单复习一下快排算法：就是在一个待排数组中找一个“代表值”，之后让这个代表值找到他应该在的地方，之后整个数组被分成两个部分，之后再左右递归该操作，完成排序，此种方法排序时间复杂度为O（NlogN),但是当一整个数组都为一个数时，时间复杂度会退化为O（N^2),不是很推荐！

那么，我们可以利用三指针方法来实现快排，具体操作跟颜色那个题是一模一样的，这里就做一些补充~

1）“代表值”的寻找：可以取中间值，也可以取随机值，这里我们采用后者

2）随机值的获得：我们要种下一颗随机数种子，之后rand函数获得随机下标，进而获得随机数

3）随机下标的获取：设r=rand();则r%(right-left+1)为下标偏移量，之后在加上Left就好了

class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//种下一颗随机数种子qsort(nums,0,nums.size()-1);return nums;}//快排void qsort(vector<int>& nums,int l,int r)    //l对应左下标，r对应右下标{if(l>=r) return;      //说明数组至多一个数字//数据分三块int key=GetRandom(nums,l,r);int i=l,left=l-1,right=r+1;while(i<right){if(nums[i]<key) swap(nums[++left],nums[i++]);else if(nums[i]==key) i++;else swap(nums[--right],nums[i]);}//[l,left] [left+1,right-1] [right,r]//再对左右两部分进行快排qsort(nums,l,left);qsort(nums,right,r);}int GetRandom(vector<int>& nums,int left,int right){int r=rand()%(right-left+1)+left;return nums[r];}
};

3.数组中的第K个最大元素

215. 数组中的第K个最大元素 - 力扣（LeetCode）

解题思路：

这个就是我之前在数据结构那一专栏总结的Topk问题，这里我还是用快排解决一下吧~

注：本题是在上一道题的基础上进一步深入，请确保已经理解了前面的内容~

我们还是通过key值将数组分成如下的三段：

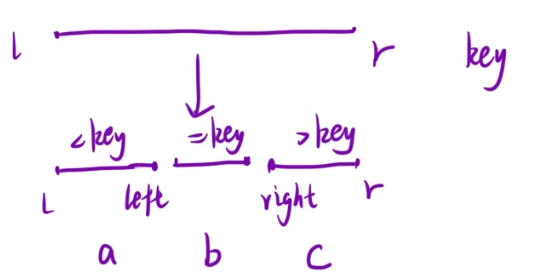
之后我们开始分类讨论：

1）c>=k      ->   在[right,r]里面找

2）b+c>=k   ->   返回key

3）1和2不成立  ->在[l,left],找第k-b-c大的

class Solution {
public:int findKthLargest(vector<int>& nums, int k) {return qsort(nums,0,nums.size()-1,k);}int qsort(vector<int>& nums,int l,int r,int k){if(l==r) return nums[l];//1.选择随机元素int key=GetRandom(nums,l,r);//2.分三块int left=l-1,right=r+1,i=l;while(i<right){if(nums[i]<key) swap(nums[++left],nums[i++]);else if(nums[i]==key) i++;else swap(nums[--right],nums[i]);}//3.分情况讨论int c =r-right+1,b=right-left-1;if(c>=k) return qsort(nums,right,r,k);else if(b+c>=k) return key;else return qsort(nums,l,left,k-b-c);}int GetRandom(vector<int>& nums,int left,int right){int r=rand()%(right-left+1)+left;return nums[r];}
};

4.最小k个数

LCR 159. 库存管理 III - 力扣（LeetCode）

这道题和上一道题解法几乎相同，这里就不讲解了，仅列出一张图来辅助参考

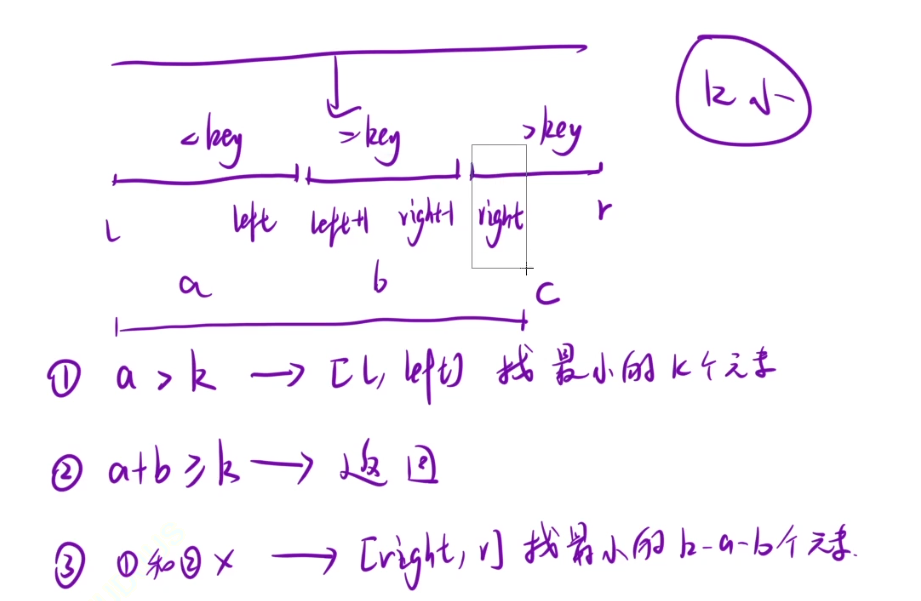
注：这里的qsort并不是要排序，只是选择而已，选出来前k个数而已，这前k个数有可能顺序还是乱的！！！

class Solution {
public:vector<int> inventoryManagement(vector<int>& stock, int cnt) {srand(time(NULL));qsort(stock,0,stock.size()-1,cnt);return {stock.begin(),stock.begin()+cnt};}void qsort(vector<int>& stock,int l,int r,int cnt){int key=GetRandom(stock,l,r);int left=l-1,right=r+1,i=l;while(i<right){if(stock[i]<key) swap(stock[++left],stock[i++]);else if(stock[i]==key) i++;else swap(stock[--right],stock[i]);}int a=left-l+1,b=right-left-1;if(a>cnt) return qsort(stock,l,left,cnt);else if(a+b>=cnt) return ;else return qsort(stock,right,r,cnt-a-b);}int GetRandom(vector<int>& stock,int l,int r){int x=rand()%(r-l+1)+l;return stock[x];}
};

分治——快排部分结束，下面将更新归并排序部分~