主成分分析加强版:MP-PCA
先来个背景:
假设我们现在有6个蛋白质样本,然后4个特征(电荷密度、疏水性、长度、柔性)
# 假设我们有6个蛋白质样本,4个特征(电荷密度、疏水性、长度、柔性)
protein_names = ['Protein_A', 'Protein_B', 'Protein_C', 'Protein_D', 'Protein_E', 'Protein_F']
feature_names = ['Charge_Density', 'Hydrophobicity', 'Length', 'Flexibility']data = np.asarray([[0.8, 0.2, 100, 0.7], # Protein_A: 高电荷,低疏水,中等长度,中高柔性[0.3, 0.9, 150, 0.4], # Protein_B: 低电荷,高疏水,长,中低柔性[0.9, 0.1, 80, 0.8], # Protein_C: 很高电荷,很低疏水,短,高柔性[0.2, 0.8, 200, 0.3], # Protein_D: 很低电荷,高疏水,很长,低柔性[0.6, 0.4, 120, 0.6], # Protein_E: 中电荷,中疏水,中长,中柔性[0.1, 1.0, 180, 0.2] # Protein_F: 最低电荷,最高疏水,长,最低柔性
])data
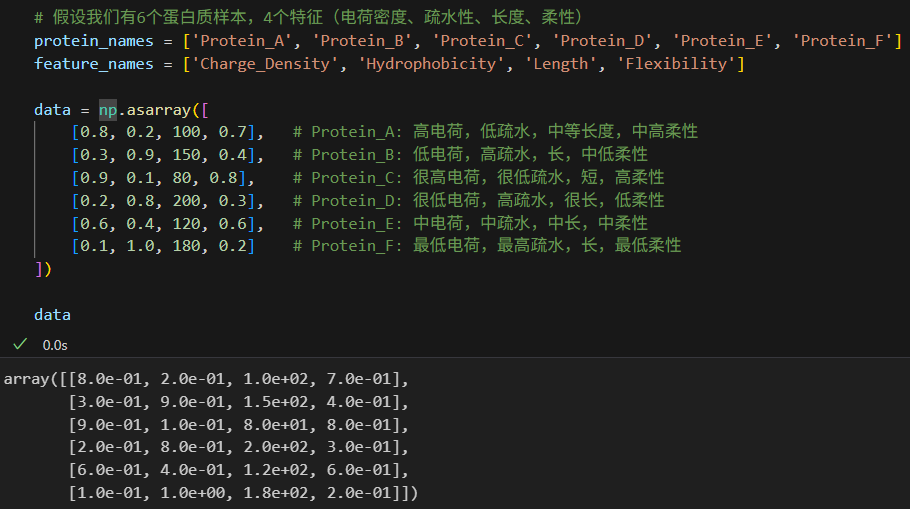
上面的data就是我们的数据矩阵,行 x 列是sample x feature=observation x variable的形式,
1,简单分析
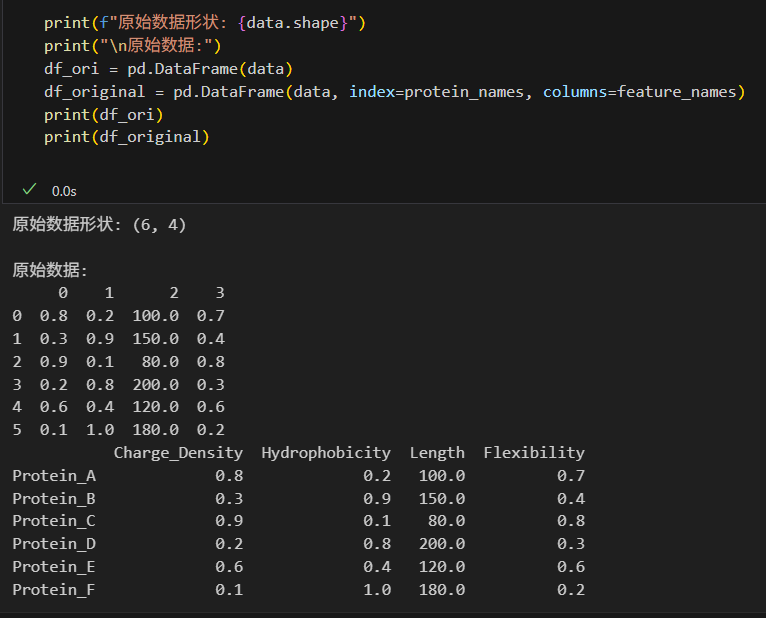
我们可以将行、列标签加上去,查看原始数据的基本形式:
print(f"原始数据形状: {data.shape}")
print("\n原始数据:")
df_ori = pd.DataFrame(data)
df_original = pd.DataFrame(data, index=protein_names, columns=feature_names)
print(df_ori)
print(df_original)
对于特征之间,我们可以查看相关性,可以使用numpy.corrcoef,
注意我们是对每个特征之间的相关性进行分析,
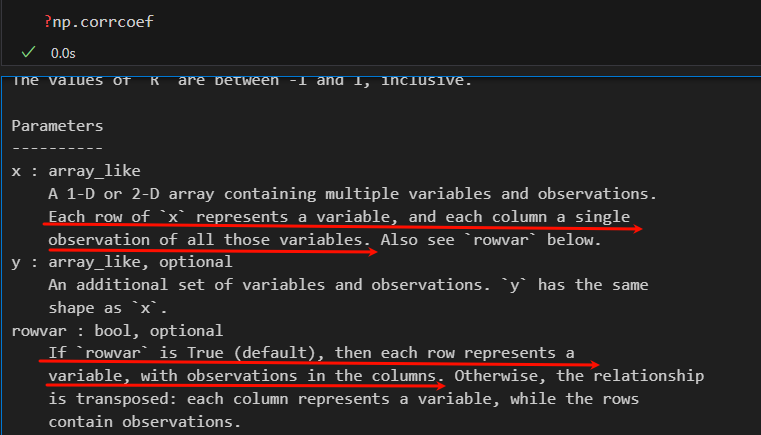
我们可以看到,这个函数是默认行是变量,也就是行是特征,列是样本也就是观测,
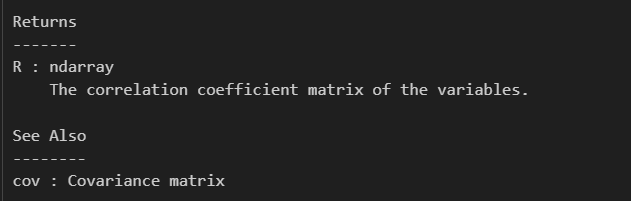
然后返回的是变量也就是特征之间的相关性分析,
对原始数据矩阵形式转化一下就可以了,
要么转置,要么使用rowvar参数
# observation x variable,等价于sample x feature
# corrcoef默认是每一行都是一个variable,也就是默认的矩阵形式是feature x sample,然后按照行x行进行相关性分析
# 所以我们的矩阵如果是sample x feature,我们就得将矩阵进行转置,将feature转置成行,然后再corrcoef
# 或者是使用参数rowvar,默认是True,也就是行作为变量(非观测,也就是行为特征)
# 所以,1️⃣数据转置,按每行1特征来 2️⃣数据不转置,设置rowvar=Falsecorrelation_matrix = np.corrcoef(data.T)
correlation_matrix
下面这个是观测x观测的,也就是6x6的
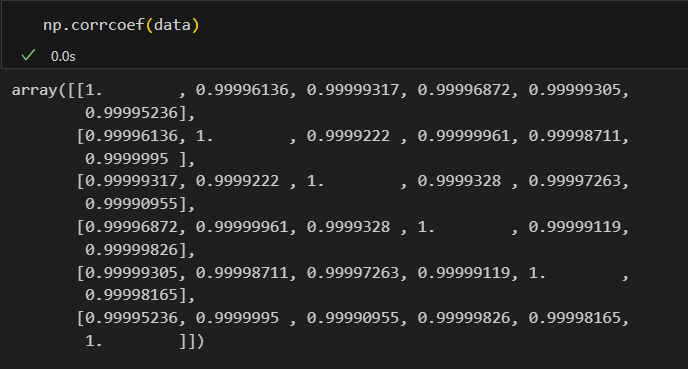
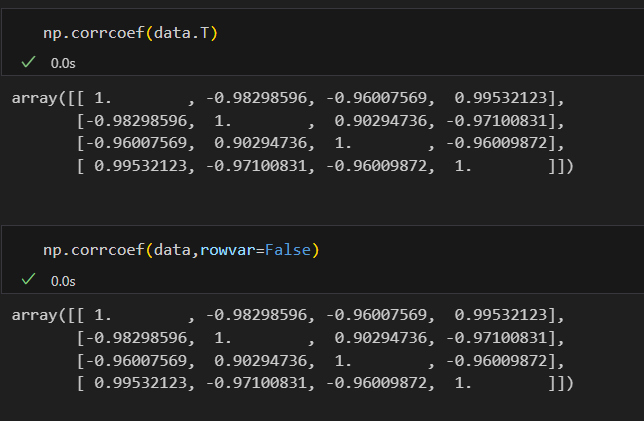
如果是对特征,也就是变量:
# 1️⃣进行数据转置
np.corrcoef(data.T)# 2️⃣使用rowvar参数
np.corrcoef(data,rowvar=False)
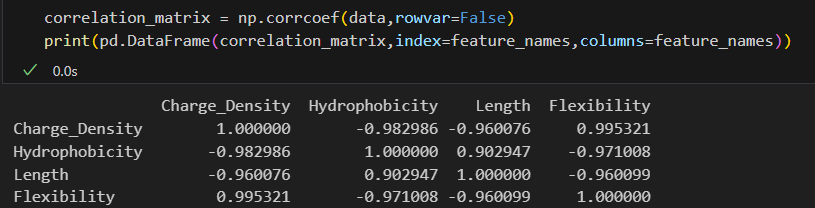
同样我们查看相关性矩阵,可以绘制一个基本的热图
correlation_matrix = np.corrcoef(data,rowvar=False)
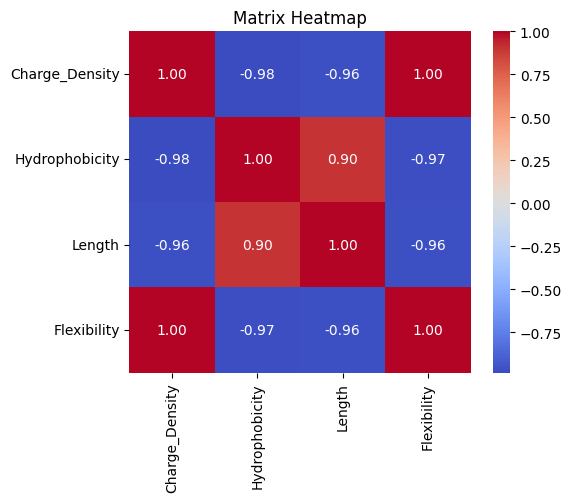
print(pd.DataFrame(correlation_matrix,index=feature_names,columns=feature_names))
(1)绘制相关性热图:
函数的输入是matrix(numpy.ndarray),或者是pandas的dataframe;
要区分的话就是看有没有values属性,有的是pd.DataFrame;
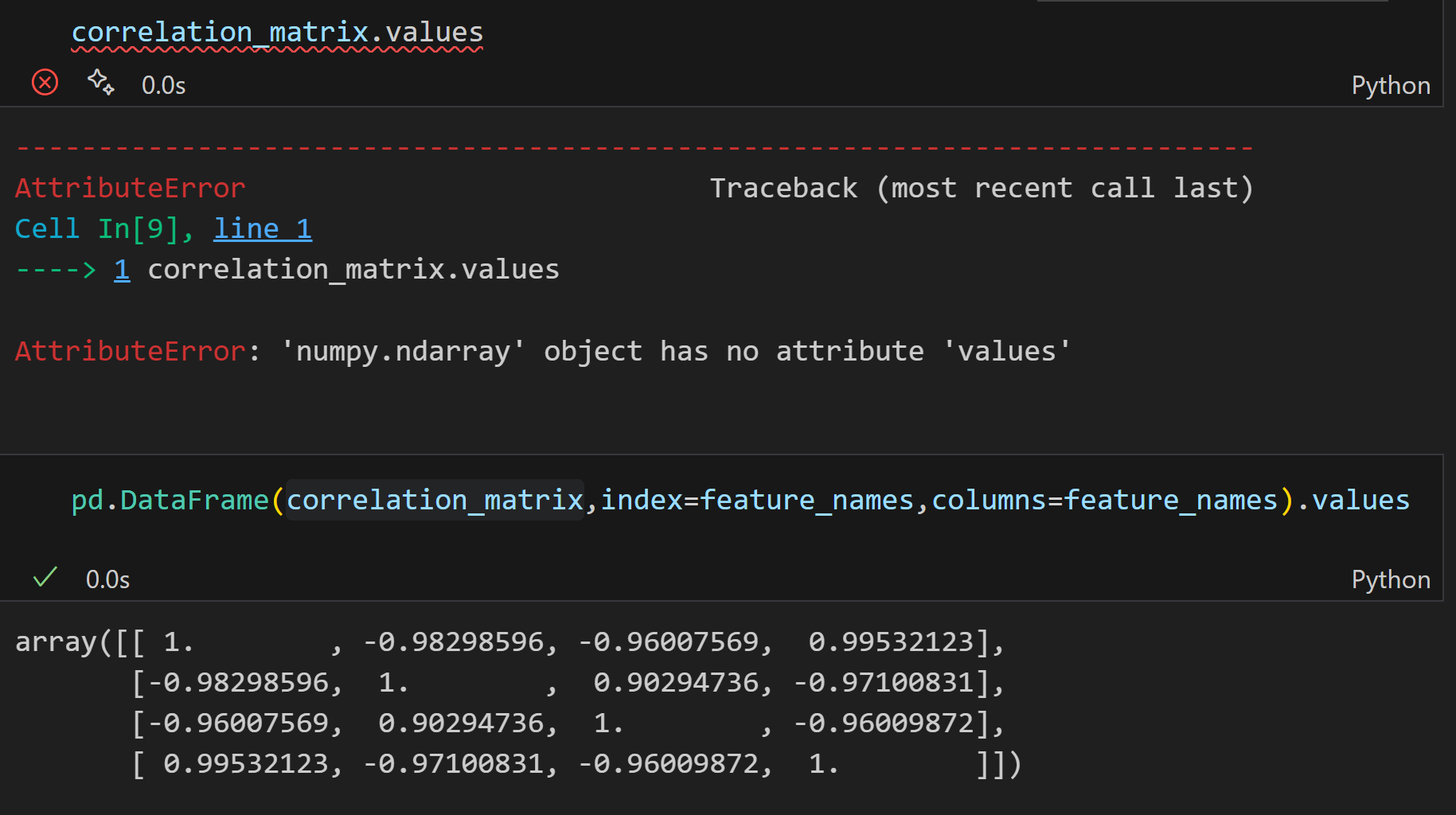
用hasattr函数判断:
至于行列标签,如果是numpy.ndarray,使用自定义的feature names;
如果是pd.DataFrame,则直接使用行列名;
函数模板见下,参考:
https://github.com/MaybeBio/bioinfor_script_modules/blob/main/30_Plot_Corr_heatmap_From_Matrix.py
def plot_matrix_heatmap(matrix,row_labels=None,col_labels=None,title="Matrix Heatmap",cmap="coolwarm",figsize=(6,5)):"""Args:matrix: 2D numpy array 或 pd.DataFramerow_labels: 行标签列表(可选)col_labels: 列标签列表(可选)title: 图标题cmap: 颜色映射figsize: 图像大小Fun:绘制矩阵或DataFrame的热图,支持自定义行列标签。"""import matplotlib.pyplot as pltimport seaborn as sns# 创建新的图形对象plt.figure(figsize=figsize)# 通过values属性判断是numpy.ndarray还是pd.DataFrameif hasattr(matrix,'values'):# 有values属性,说明是pd.DataFrame# 直接使用values属性抽取其底层的numpy数组值data = matrix.values# 如果没有提供行、列标签,则使用DataFrame的index和columnsif row_labels is None:row_labels = matrix.indexif col_labels is None:col_labels = matrix.columns# 否则,直接使用numpy数组else:data = matrix# 绘制热图sns.heatmap(data,annot=True,fmt=".2f", # 显示数值,保留两位小数cmap=cmap, # 颜色映射xticklabels=col_labels,yticklabels=row_labels,square=True, # 使单元格呈正方形cbar=True #显示颜色条)# 设置图标标题plt.title(title)# 自动调整子图参数,适当间距plt.tight_layout()# 显示图形plt.show()
如果传入的是numpy.ndarray:
# 如果传入的是numpy.ndarray
feature_names = ['Charge_Density', 'Hydrophobicity', 'Length', 'Flexibility']plot_matrix_heatmap(correlation_matrix,row_labels=feature_names,col_labels=feature_names)
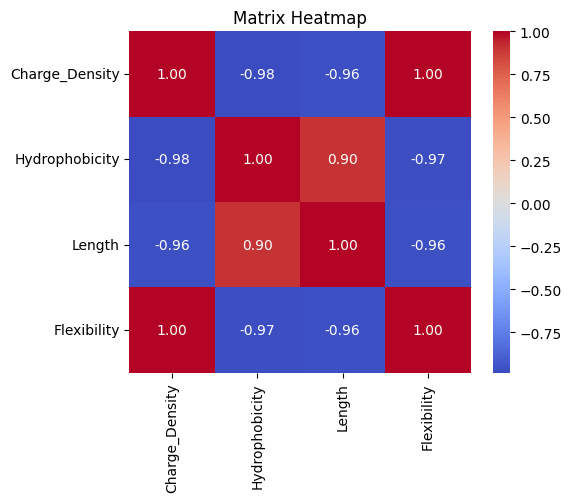
如果传入的是pd.DataFrame
# 如果传入的是pd.DataFrame,则直接使用其行列标签
df = pd.DataFrame(correlation_matrix,index=feature_names,columns=feature_names)
plot_matrix_heatmap(df)
2,PCA实现
PCA的统计学部分(也就是原理部分,线性代数那一部分)在这里就不废话了,
参考:https://github.com/MaybeBio/bioinfor_script_modules/blob/main/31_MP_PCA.py
直接进行简单的造轮子实现:
def PCA_analysis(obs_matrix,centered=True,clean_matrix=False,clean_threshold=1.0,write_PC_scores=False,write_path=''):"""Args:obs_matrix: 观测矩阵,样本x特征(我们假设输入的数据,都是每一列是1个feature)centered: 是否中心化数据clean_matrix: 是否清理矩阵(降噪处理),也就是是否要使用MP分布clean_threshold: 清理矩阵的阈值,默认1.0,也就是对MP分布极限(MP limit)的一个缩放因子,1是没有区别,如果是乘上一个大的数,就是更严格地对特征值的一个过滤 write_PC_scores: 是否保留主成分分数,默认为Falsewrite_path: 主成分得分文件输出路径(如果write_PC_scores为True)Fun:传入观测矩阵,格式为(nsamples,nfeatures),可选择是否进行均值中心化 + 标准化归一化(默认为True);PCA分析,返回特征值、特征向量和主成分得分"""import numpy as npimport os# 首先是数据预处理,也就是数据中心化以及标准化# 注意是对每一列的特征进行处理,所以要注意axis参数(我之前博客中提到过这个轴的记忆口诀,就是行0行,列1列)if centered:mean_vec = np.mean(obs_matrix,axis=0)std_vec = np.std(obs_matrix,axis=0)# 然后就是归一化之后的数据z_matrix = (obs_matrix-mean_vec)/std_vec# 如果不进行标准化处理,则使用原始观测矩阵else:z_matrix = obs_matrix# 然后就是计算协方差矩阵# 计算协方差矩阵:X^T * X / (n-1)# 此处使用除以样本数-1,是为了获取无偏估计cov_mat = (z_matrix).T.dot(z_matrix)/ (z_matrix.shape[0]-1)# 在计算出协方差矩阵之后就是特征值分解,获取特征值和特征向量eig_vals,eig_vecs = np.linalg.eig(cov_mat)# 然后对特征值进行排序,降序排列key = np.argsort(eig_vals)[::-1]# 然后特征值和特征向量按照排序之后的索引重新组织,都是降序eig_vals,eig_vecs = eig_vals[key],eig_vecs[:,key] # 如果需要清理矩阵,也就是降噪处理# 此处使用随机矩阵理论中的Marchenko-Pastur Distribution,也就是MP分布,来决定哪些特征值是我们想要的、哪些不是我们想要的,也就是降噪if clean_matrix:# 在计算MP分布的时候,我们需要sample/feature数的比值,实际上就是Accept ratios_f_ratio = obs_matrix.shape[0]/(obs_matrix.shape[1])# 然后就是计算MP limit(上界),即符合MP分布的最大特征值,此处公式需要数学验证⚠️lamda_max = 1 + 1/s_f_ratio + 2/np.sqrt(s_f_ratio)# 依据MP分布的上界和阈值,找到需要清理的特征值# 注意这里的clean_threshold是一个缩放因子,默认1.0,也就是MP分布的极限# 如果需要更严格的清理,可以将clean_threshold设置为大于1的# 找到第1个小于阈值的特征值位置pos = np.where(eig_vals < clean_threshold*lamda_max)[0][0]# 重构清理后的协方差矩阵,保留前pos个主成分(因为是降序排列的)cleaned_cov = (eig_vecs[:,:pos].dot(np.diag(eig_vals[:pos]))).dot(eig_vecs[:,:pos].T)#重新计算清理后矩阵的特征值和特征向量eig_vals,eig_vecs = np.linalg.eig(cleaned_cov)# 再次按照特征值大小进行降序排列key = np.argsort(eig_vals)[::-1]eig_vals,eig_vecs = eig_vals[key],eig_vecs[:,key]# 计算主成分得分:原始数据投影到主成分空间pc_scores = (z_matrix.dot(eig_vecs)).astype(float)# 如果需要保存主成分得分if write_PC_scores:# 创建标签列:pc_1,pc_2...col_labels = ['pc_'+str(x+1) for x in range(len(eig_vals))]# 创建dataframedf = pd.DataFrame(pc_scores,column=col_labels)os.makedirs(write_path,exist_ok=True)# 构建文件名,包含清理标志file_name = write_path +'/pca_clean_' + str(clean_matrix)+".csv"# 保存为csv文件df.to_csv(file_name)# 返回特征值、特征向量、主成分得分return eig_vals,eig_vecs,pc_scores再简化点的版本:
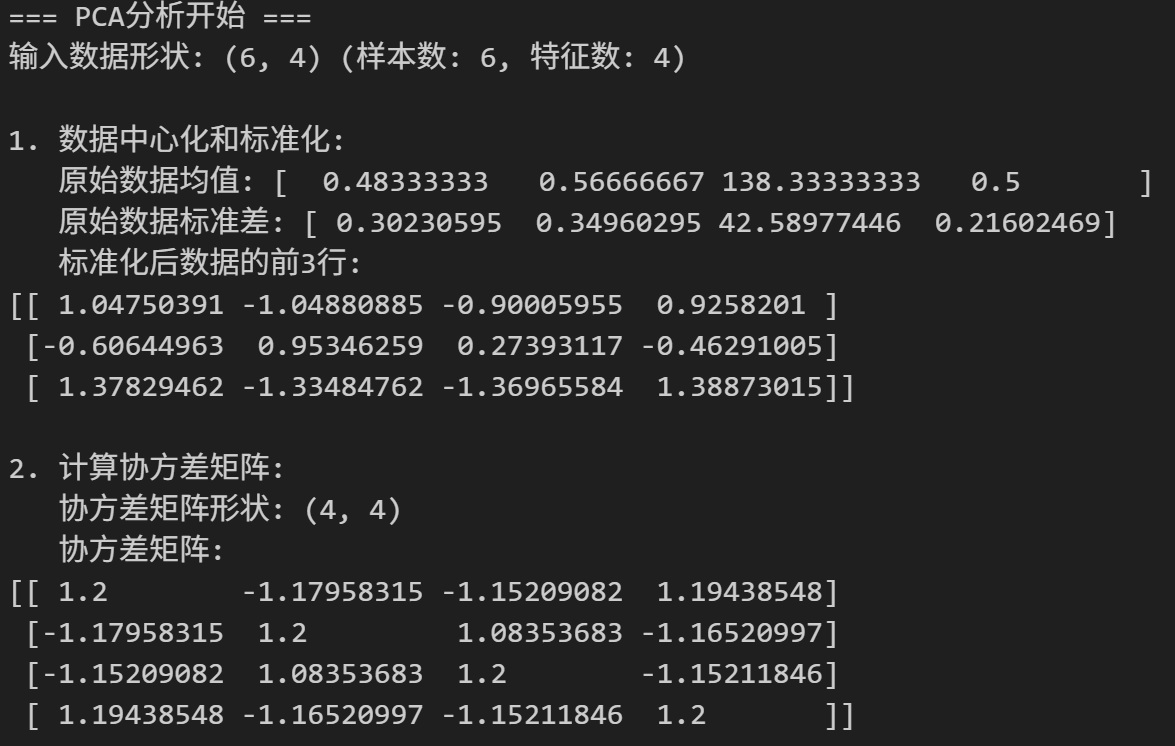
def PCA_analysis(obs_matrix, centered=True, clean_matrix=False, clean_threshold=2.0):"""PCA主成分分析函数"""print("=== PCA分析开始 ===")print(f"输入数据形状: {obs_matrix.shape} (样本数: {obs_matrix.shape[0]}, 特征数: {obs_matrix.shape[1]})")# 数据预处理if centered:print("\n1. 数据中心化和标准化:")mean_vec = np.mean(obs_matrix, axis=0)std_vec = np.std(obs_matrix, axis=0)print(f" 原始数据均值: {mean_vec}")print(f" 原始数据标准差: {std_vec}")z_matrix = (obs_matrix - mean_vec) / std_vecprint(f" 标准化后数据的前3行:\n{z_matrix[:3]}")else:z_matrix = obs_matrix# 计算协方差矩阵print("\n2. 计算协方差矩阵:")cov_mat = (z_matrix).T.dot(z_matrix) / (z_matrix.shape[0] - 1)print(f" 协方差矩阵形状: {cov_mat.shape}")print(f" 协方差矩阵:\n{cov_mat}")# 特征值分解print("\n3. 特征值分解:")eig_vals, eig_vecs = np.linalg.eig(cov_mat)print(f" 原始特征值: {eig_vals}")print(f" 特征向量矩阵形状: {eig_vecs.shape}")# 按特征值大小降序排列key = np.argsort(eig_vals)[::-1]eig_vals, eig_vecs = eig_vals[key], eig_vecs[:, key]print(f" 排序后特征值: {eig_vals}")print(f" 解释方差比例: {eig_vals / np.sum(eig_vals)}")# 矩阵清理(如果需要)if clean_matrix:print("\n4. 矩阵清理(Marchenko-Pastur):")q = obs_matrix.shape[0] / obs_matrix.shape[1]lambda_max = 1 + 1/q + 2/np.sqrt(q)print(f" 样本/特征比值 q: {q:.3f}")print(f" Marchenko-Pastur上界: {lambda_max:.3f}")print(f" 清理阈值: {clean_threshold * lambda_max:.3f}")noise_indices = np.where(eig_vals < clean_threshold * lambda_max)[0]if len(noise_indices) > 0:pos = noise_indices[0]print(f" 保留前 {pos} 个主成分")cleaned_cov = (eig_vecs[:, :pos] @ np.diag(eig_vals[:pos])) @ eig_vecs[:, :pos].Teig_vals, eig_vecs = np.linalg.eig(cleaned_cov)key = np.argsort(eig_vals)[::-1]eig_vals, eig_vecs = eig_vals[key], eig_vecs[:, key]print(f" 清理后特征值: {eig_vals}")# 计算主成分得分print("\n5. 计算主成分得分:")pc_scores = (z_matrix @ eig_vecs).astype(float)print(f" 主成分得分形状: {pc_scores.shape}")print(f" 前3个样本的PC得分:\n{pc_scores[:3]}")return eig_vals, eig_vecs, pc_scores
对前面的数据进行分析:
# 假设我们有6个蛋白质样本,4个特征(电荷密度、疏水性、长度、柔性)
protein_names = ['Protein_A', 'Protein_B', 'Protein_C', 'Protein_D', 'Protein_E', 'Protein_F']
feature_names = ['Charge_Density', 'Hydrophobicity', 'Length', 'Flexibility']data = np.asarray([[0.8, 0.2, 100, 0.7], # Protein_A: 高电荷,低疏水,中等长度,中高柔性[0.3, 0.9, 150, 0.4], # Protein_B: 低电荷,高疏水,长,中低柔性[0.9, 0.1, 80, 0.8], # Protein_C: 很高电荷,很低疏水,短,高柔性[0.2, 0.8, 200, 0.3], # Protein_D: 很低电荷,高疏水,很长,低柔性[0.6, 0.4, 120, 0.6], # Protein_E: 中电荷,中疏水,中长,中柔性[0.1, 1.0, 180, 0.2] # Protein_F: 最低电荷,最高疏水,长,最低柔性
])dataPCA_analysis(data)
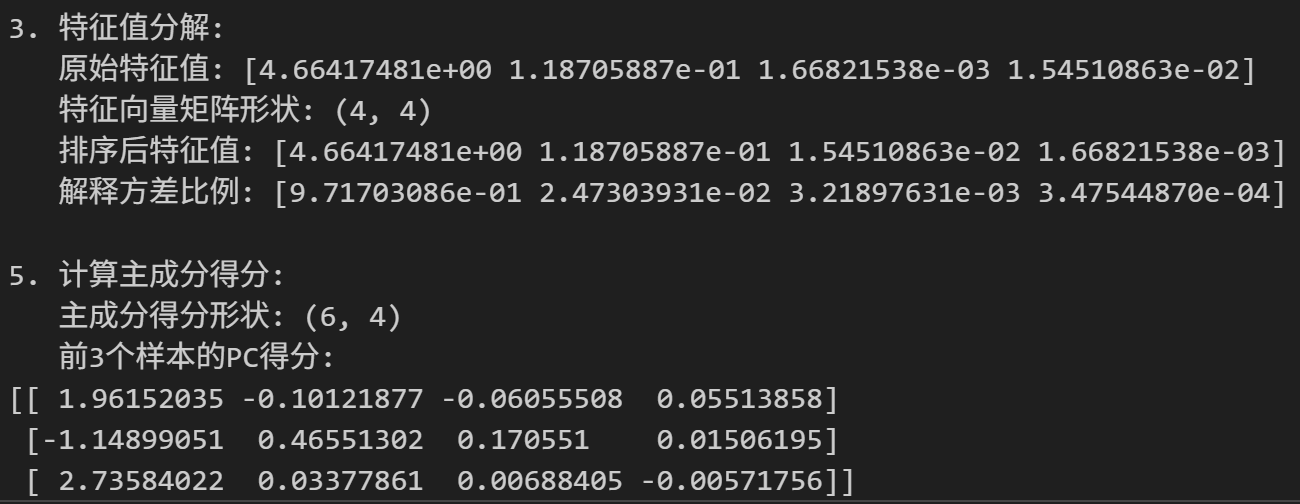
如果使用MP分布(1阈值)作为阈值清理噪声(MP分布见下细节解释部分):

使用前面背景中的数据矩阵data,加上简化的PCA函数,
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
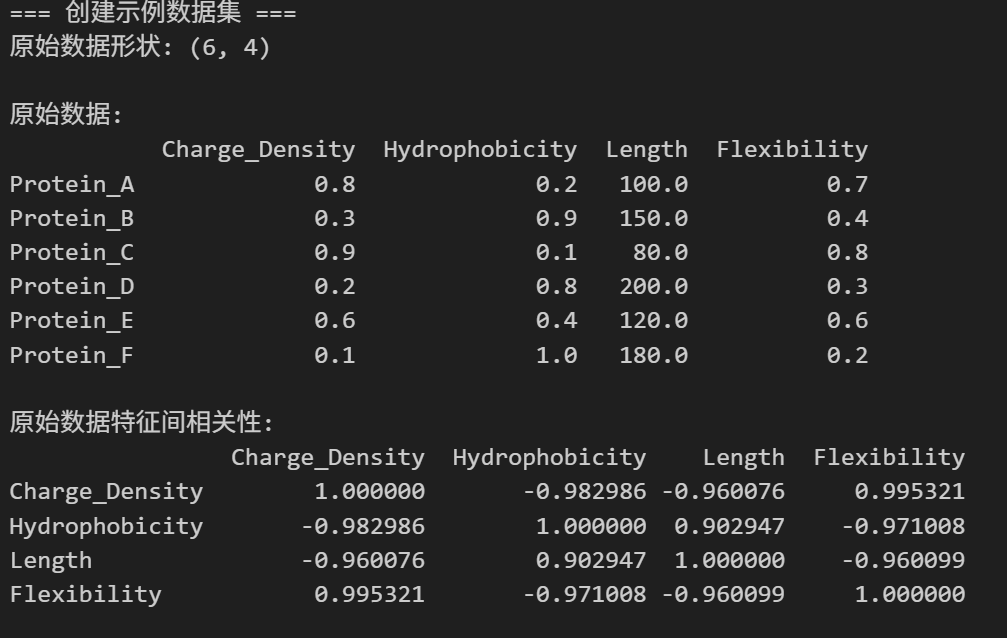
import seaborn as sns# 创建示例数据集:蛋白质特征数据
np.random.seed(2025)print("=== 创建示例数据集 ===")
# 假设我们有6个蛋白质样本,4个特征(电荷密度、疏水性、长度、柔性)
protein_names = ['Protein_A', 'Protein_B', 'Protein_C', 'Protein_D', 'Protein_E', 'Protein_F']
feature_names = ['Charge_Density', 'Hydrophobicity', 'Length', 'Flexibility']# 创建具有内在相关性的数据
# 电荷密度和疏水性负相关,长度和柔性正相关
data = np.array([[0.8, 0.2, 100, 0.7], # Protein_A: 高电荷,低疏水,中等长度,中高柔性[0.3, 0.9, 150, 0.4], # Protein_B: 低电荷,高疏水,长,中低柔性[0.9, 0.1, 80, 0.8], # Protein_C: 很高电荷,很低疏水,短,高柔性[0.2, 0.8, 200, 0.3], # Protein_D: 很低电荷,高疏水,很长,低柔性[0.6, 0.4, 120, 0.6], # Protein_E: 中电荷,中疏水,中长,中柔性[0.1, 1.0, 180, 0.2] # Protein_F: 最低电荷,最高疏水,长,最低柔性
])print(f"原始数据形状: {data.shape}")
print("\n原始数据:")
df_original = pd.DataFrame(data, index=protein_names, columns=feature_names)
print(df_original)# 计算原始数据的相关性矩阵
print("\n原始数据特征间相关性:")
correlation_matrix = np.corrcoef(data.T)
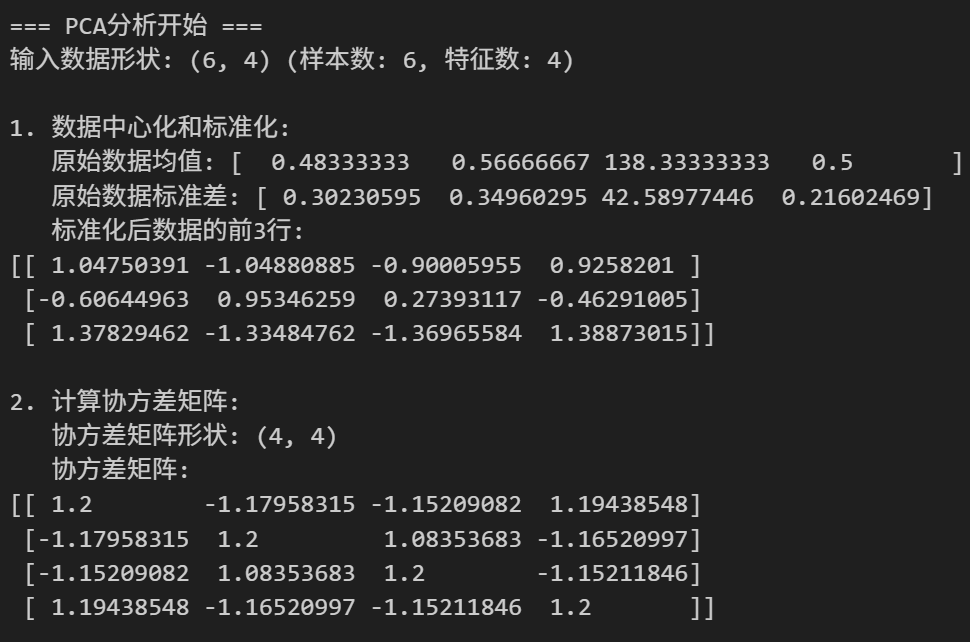
print(pd.DataFrame(correlation_matrix, index=feature_names, columns=feature_names))# 执行PCA分析
print("\n" + "="*60)
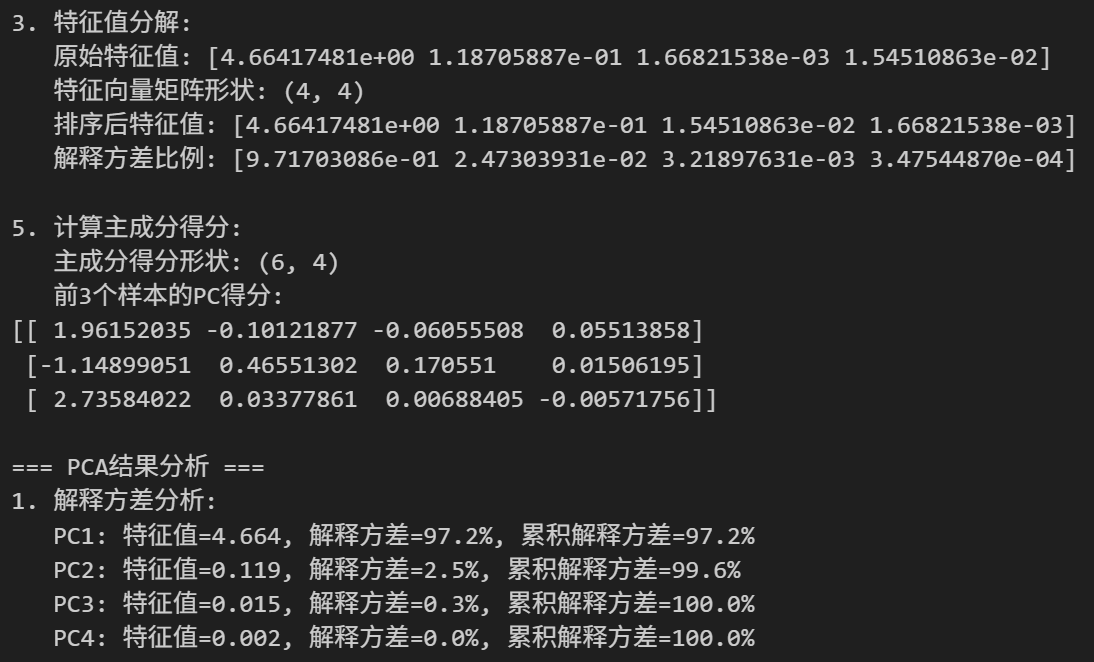
eig_vals, eig_vecs, pc_scores = PCA_analysis(data, centered=True, clean_matrix=False)# 详细分析结果
print("\n=== PCA结果分析 ===")# 1. 解释方差分析
explained_variance_ratio = eig_vals / np.sum(eig_vals)
cumulative_variance = np.cumsum(explained_variance_ratio)print("1. 解释方差分析:")
for i, (val, ratio, cum) in enumerate(zip(eig_vals, explained_variance_ratio, cumulative_variance)):print(f" PC{i+1}: 特征值={val:.3f}, 解释方差={ratio:.1%}, 累积解释方差={cum:.1%}")# 2. 主成分的含义分析
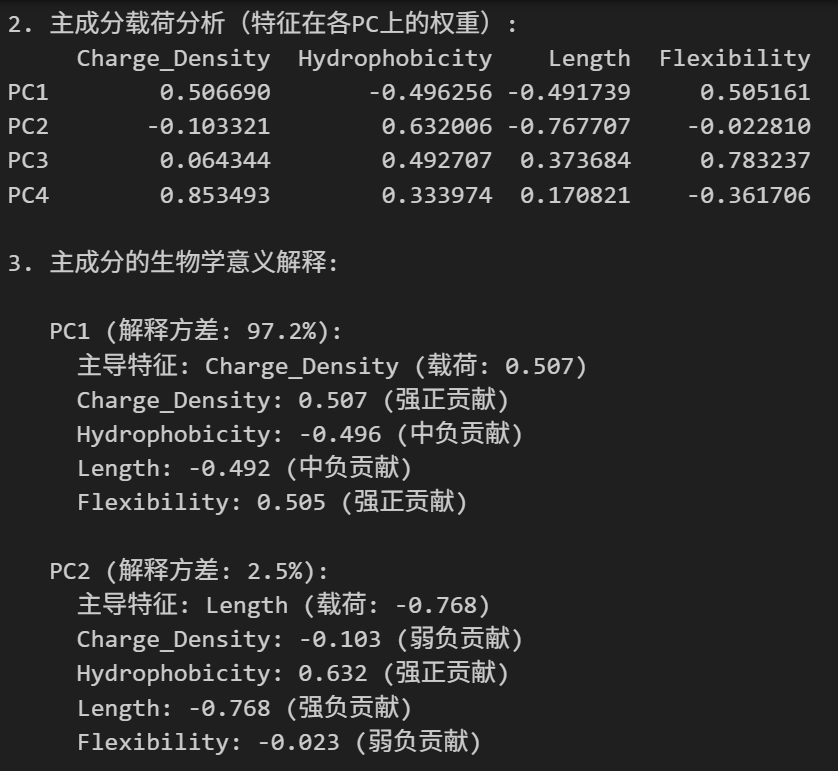
print("\n2. 主成分载荷分析(特征在各PC上的权重):")
loadings_df = pd.DataFrame(eig_vecs.T, columns=feature_names, index=[f'PC{i+1}' for i in range(len(eig_vals))])
print(loadings_df)# 解释主成分的生物学意义
print("\n3. 主成分的生物学意义解释:")
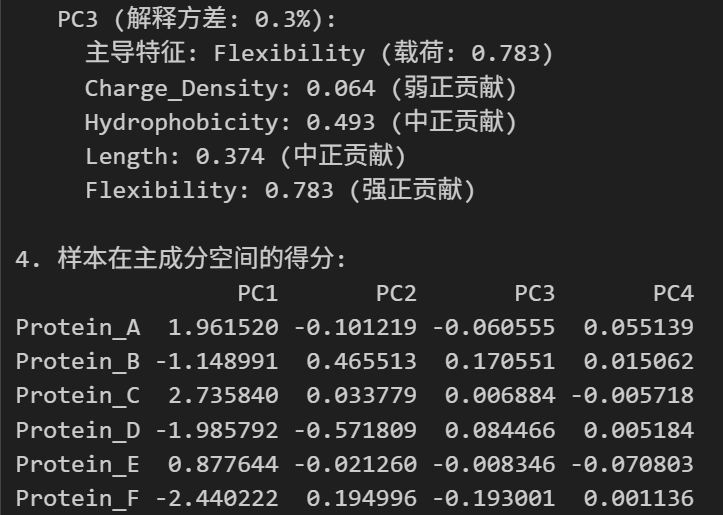
for i in range(min(3, len(eig_vals))): # 分析前3个主成分print(f"\n PC{i+1} (解释方差: {explained_variance_ratio[i]:.1%}):")loadings = eig_vecs[:, i]# 找出载荷最大的特征max_idx = np.argmax(np.abs(loadings))max_feature = feature_names[max_idx]max_loading = loadings[max_idx]print(f" 主导特征: {max_feature} (载荷: {max_loading:.3f})")# 分析各特征的贡献for j, (feature, loading) in enumerate(zip(feature_names, loadings)):contribution = "正贡献" if loading > 0 else "负贡献"strength = "强" if abs(loading) > 0.5 else "中" if abs(loading) > 0.3 else "弱"print(f" {feature}: {loading:.3f} ({strength}{contribution})")# 3. 样本在主成分空间的分布
print("\n4. 样本在主成分空间的得分:")
pc_scores_df = pd.DataFrame(pc_scores, index=protein_names, columns=[f'PC{i+1}' for i in range(pc_scores.shape[1])])
print(pc_scores_df)# 可视化分析
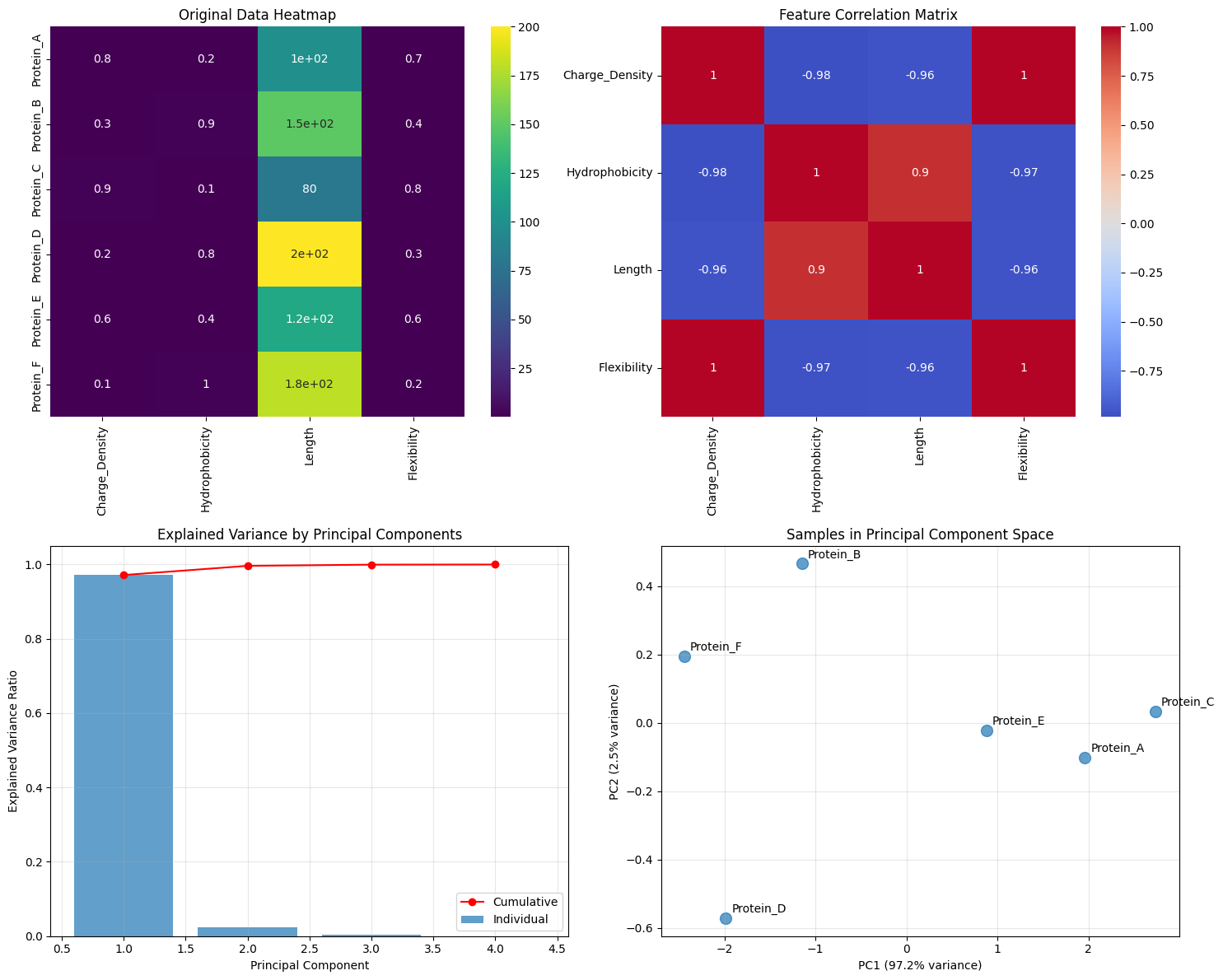
fig, axes = plt.subplots(2, 2, figsize=(15, 12))# 1. 原始数据热图
sns.heatmap(df_original, annot=True, cmap='viridis', ax=axes[0,0])
axes[0,0].set_title('Original Data Heatmap')# 2. 特征相关性热图
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', center=0, xticklabels=feature_names, yticklabels=feature_names, ax=axes[0,1])
axes[0,1].set_title('Feature Correlation Matrix')# 3. 解释方差比例
axes[1,0].bar(range(1, len(eig_vals)+1), explained_variance_ratio, alpha=0.7, label='Individual')
axes[1,0].plot(range(1, len(eig_vals)+1), cumulative_variance, 'ro-', label='Cumulative')
axes[1,0].set_xlabel('Principal Component')
axes[1,0].set_ylabel('Explained Variance Ratio')
axes[1,0].set_title('Explained Variance by Principal Components')
axes[1,0].legend()
axes[1,0].grid(True, alpha=0.3)# 4. 主成分得分散点图
scatter = axes[1,1].scatter(pc_scores[:, 0], pc_scores[:, 1], s=100, alpha=0.7)
for i, protein in enumerate(protein_names):axes[1,1].annotate(protein, (pc_scores[i, 0], pc_scores[i, 1]), xytext=(5, 5), textcoords='offset points')
axes[1,1].set_xlabel(f'PC1 ({explained_variance_ratio[0]:.1%} variance)')
axes[1,1].set_ylabel(f'PC2 ({explained_variance_ratio[1]:.1%} variance)')
axes[1,1].set_title('Samples in Principal Component Space')
axes[1,1].grid(True, alpha=0.3)plt.tight_layout()
plt.show()
一些需要注意细节的地方:
(1)协方差矩阵的计算
参考https://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE,


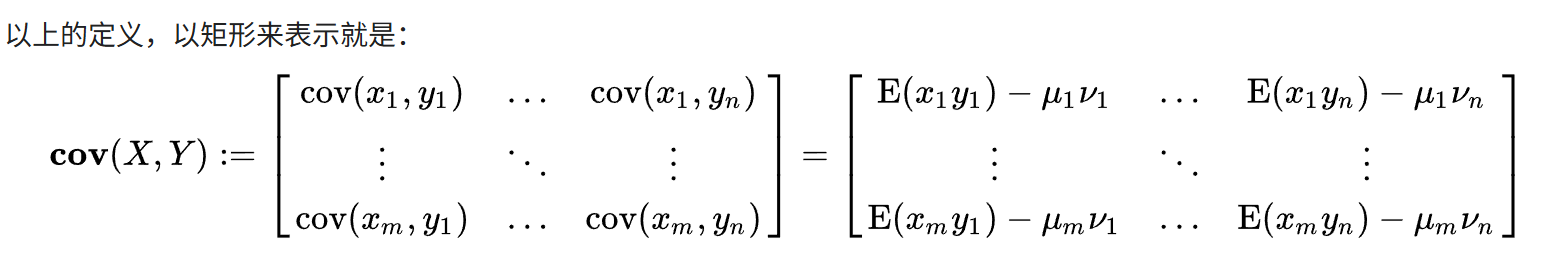
我们的每一列feature都是一个随机变量,我们的协方差矩阵实际上就是任意两列feature之间的协方差计算;
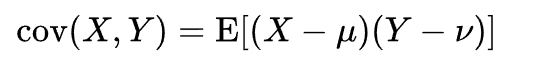
依据上面的这个公式,我们前面做中心化以及标准化处理,实际上就是为了在计算协方差的时候能够让上面公式里的两个期望参数为0,这样便于计算协方差。
另外我们展开来看:
如果有两列feature_i,以及feature_j,
我们在计算cov(i,j)的时候,实际上计算的就是这两个随机变量的点乘(dot product),然后再做一个平均。
所以对于前面中心化+标准化之后的矩阵,比如说z_matrix,
实际上我们只需要z_matrix * (z_matrix.T),就能够计算任意两列向量也就是任意两个feature之间的点积了,也就满足前面做过中心化+标准化的矩阵的协方差公式;
然后我们再对样本倒数做一个加权,为了获取无偏的协方差估计。
这也就是:
cov_mat = (z_matrix).T.dot(z_matrix)/ (z_matrix.shape[0]-1)
(2)特征值和特征向量的计算
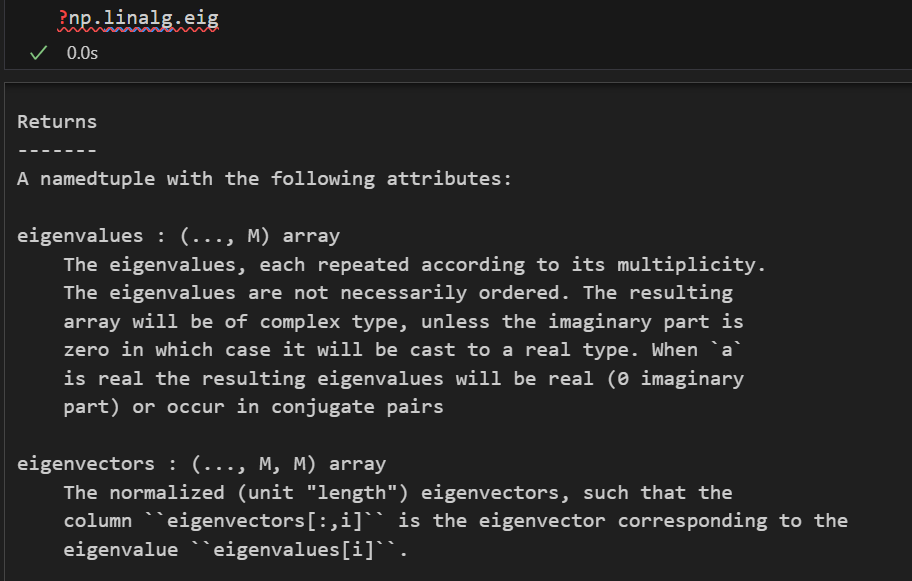
主要使用numpy.linalg分解特征值、特征向量
import numpy as np
from numpy import linalg as LAeigenvalues, eigenvectors = LA.eig(你的协方差矩阵))
再次注意,我们对数据的处理,包括中心化、以及标准化等,都是针对于feature特征数据进行的,
注意axis轴参数的选择,以及使用(我之前的博客中也提到过axis口诀,就是行0行,列1列);
按行对某一列特征求均值、求方差。
然argsort是默认使用lats axis,最后1个轴,即1,也就是按列,也就是对每一行逐列进行排序,然后argsort默认是升序排列,所以在获取排序结果之后需要逆序,也就是[::-1]。
(3)降噪与Marchenko-Pastur分布,即MP-PCA
马尔琴科—巴斯德分布(Marchenko-Pastur distribution),一般在一些工科研究生阶段的随机矩阵理论+数据科学相关授课内容的时候会涉及到,
参考:
https://en.wikipedia.org/wiki/Marchenko%E2%80%93Pastur_distribution
https://www.wolfram.com/language/11/random-matrices/marchenko-pastur-distribution.html.zh?footer=lang
https://www.math.pku.edu.cn/teachers/yaoy/Fall2011/lecture03.pdf
https://medium.com/@affanhamid007/the-marcenko-pastur-theorem-and-its-use-in-portfolio-allocation-3cbe2d976606



前面的概念不是此次的重点,重点是将MP分布应用于相关矩阵上,

这里计算的是观测/变量,也就是样本/特征的一个值;
其实就是在计算MP分布极限(The Marcenko-Pastur Limits)时的Aspect ratio;

简单来说:
MP分布描述了随机矩阵的经验谱分布的渐近行为,比如说考虑一个p x n的随机矩阵X,当p、n趋向于无穷,且矩阵维度(此处对应我们的feature维度)/自由度(此处对应我们的样本数目,sample维度),也就是p/n趋向于1个常数c∈(0,无穷大)时,样本协方差矩阵S=1/n (X X^T)的特征值会收敛到MP分布。
MP分布可以看作是描述随机矩阵奇异值的一种分布,或者说满足一定前提条件下的随机矩阵,其奇异值应满足的一种分布(当然,奇异值和特征值的区别与联系,是最基础的本科生也应该了解的矩阵理论常识,此处不提);
简单来说,MP分布在形式上近似地模拟了大量随机矩阵的奇异值的分布。因此,对于观测数量(sample)和特征数量(feature)都很大的数据集,我们一般使用的规则是只保留拟合的MP分布支持之外的特征值,但是注意,MP分布用于决定要保留的维数,一般仅在数据集至少包含多个sample、feature的情况下使用(比如说超大型矩阵,samplexfeature都是几千维的)。
所以再次简单来说,我们这里使用MP分布来完善PCA分析,实际上只是为了能够决定哪些特征值我们是要的、哪些是我们不要的,也就是利用MP分布来决定PCA降维的维度,也就是利用MP分布来降噪,也就是滤波filter。
总之,我们就是利用MP分布的一个极限(MP limit)来选取主成分PCs
类似的工具有很多,暂时没有在sklearn的实现中发现
from sklearn.decomposition import PCA
随便举一个R中的例子,比如说参考:https://rdrr.io/bioc/PCAtools/man/chooseMarchenkoPastur.html

MP分布极限(MP limit)定义的是最大的特征值,
其物理意义,有很多统计学、数据科学交叉方面的参考资料,
我个人一般简单解读为纯随机噪声产生的最大特征值的理论上界,
然后实际在数据科学(也就是此处PCA,或者是更一般的奇异值分解SVD问题),我们一般认为超出此阈值的特征值包含真实信号,低于此阈值的被视为噪声noise;
然后我代码中的分布极限,其实使用的推导如下:
真实推导过程中需要了解MP分布概率密度函数,也就是PDF函;


简单推导总结如下(我敲的markdown格式,⚠️仅供参考,仅代表个人理解****⚠️)


顺便做一个简单的可视化,更好理解,仅是个人草稿(仅供参考!)
import numpy as np
import matplotlib.pyplot as pltdef visualize_mp_theory(q_values=[0.5, 1.0, 2.0, 5.0]):"""可视化MP分布理论"""fig, axes = plt.subplots(2, 2, figsize=(15, 10))axes = axes.ravel()for i, q in enumerate(q_values):# 计算MP分布参数c = 1/qsigma_sq = 1 # 标准化后# 计算支撑区间lambda_minus = sigma_sq * (1 - np.sqrt(c))**2lambda_plus = sigma_sq * (1 + np.sqrt(c))**2# 验证公式formula_result = 1 + 1/q + 2/np.sqrt(q)# 生成MP分布if lambda_minus >= 0:lambdas = np.linspace(lambda_minus, lambda_plus, 1000)# MP密度函数numerator = np.sqrt((lambda_plus - lambdas) * (lambdas - lambda_minus))denominator = 2 * np.pi * c * lambdasdensity = numerator / denominatorelse:# 当c>1时,存在点质量在0处lambdas = np.linspace(0.001, lambda_plus, 1000)numerator = np.sqrt((lambda_plus - lambdas) * np.maximum(lambdas - 0, 0))denominator = 2 * np.pi * c * lambdasdensity = numerator / denominator# 绘制axes[i].plot(lambdas, density, 'b-', linewidth=2, label='MP density')axes[i].axvline(lambda_plus, color='r', linestyle='--', linewidth=2, label=f'Upper bound: {lambda_plus:.3f}')axes[i].axvline(formula_result, color='g', linestyle=':', linewidth=2, label=f'Formula: {formula_result:.3f}')axes[i].set_title(f'q = {q} (samples/features = {q})')axes[i].set_xlabel('Eigenvalue λ')axes[i].set_ylabel('Density')axes[i].legend()axes[i].grid(True, alpha=0.3)print(f"q = {q}:")print(f" 理论上界: {lambda_plus:.6f}")print(f" 公式计算: {formula_result:.6f}")print(f" 误差: {abs(lambda_plus - formula_result):.2e}")print()plt.tight_layout()plt.show()visualize_mp_theory()

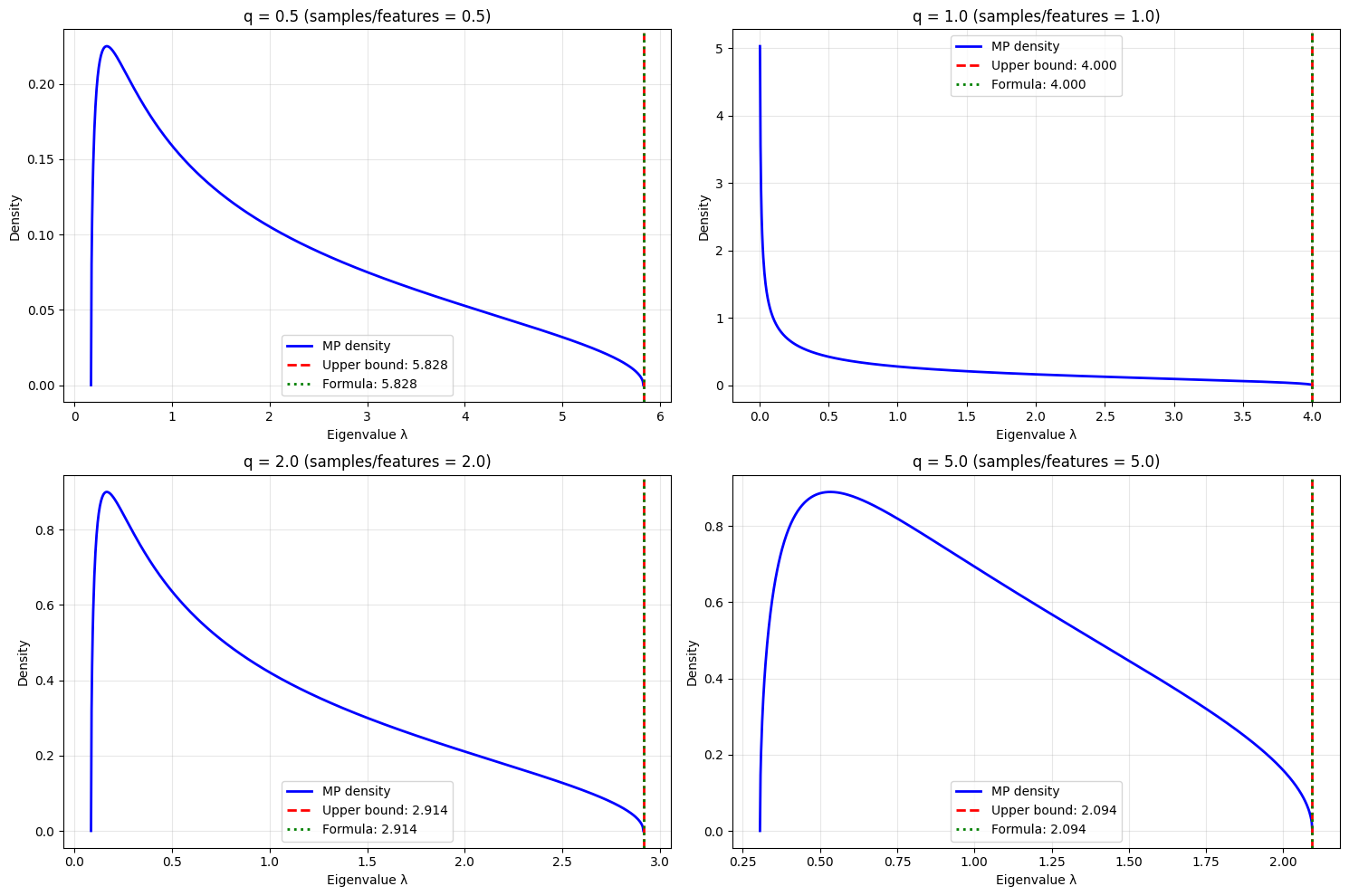
我的代码中的clean_threshold,也是一个主观的超参数,仅供参考!
def understand_noise_filtering():"""理解噪声过滤的原理"""print("=== 噪声过滤原理 ===")print("1. 理论基础:")print(" - 纯噪声数据的协方差矩阵特征值应该符合MP分布")print(" - 真实信号会产生超出MP上界的大特征值")print(" - 小于某个阈值的特征值被认为是噪声")print("\n2. 阈值设定:")print(" threshold = clean_threshold × λₘₐₓ")print(" - clean_threshold通常取2.0-3.0")print(" - 这提供了额外的安全边际")print("\n3. 实际意义:")print(" - λ > threshold: 认为包含真实信号")print(" - λ < threshold: 认为是噪声,可以过滤")# 演示不同q值下的阈值q_values = [0.1, 0.5, 1.0, 2.0, 5.0, 10.0]clean_threshold = 2.0print(f"\n4. 不同q值下的噪声阈值 (clean_threshold = {clean_threshold}):")for q in q_values:lambda_max = 1 + 1/q + 2/np.sqrt(q)threshold = clean_threshold * lambda_maxprint(f" q = {q:4.1f}: λₘₐₓ = {lambda_max:6.3f}, 阈值 = {threshold:6.3f}")understand_noise_filtering()

⚠️注意这里的clean_threshold,是我自己定义处理的一个值,依据个人经验来定,如果clean_threshold=1,就和前面所描述的一般情况符合了,只不过是我个人在分解特征值的时候,所加入的一个强限制。
我们可以看一下这个分布所预测的一个误差是如何的,
def numerical_verification():"""数值验证MP理论"""np.random.seed(2025)# 不同的q值q_values = [0.5, 1.0, 2.0]n_trials = 100for q in q_values:print(f"\n=== 验证 q = {q} ===")# 设定矩阵维度if q >= 1:p = 50 # 特征数n = int(p * q) # 样本数else:n = 100 # 样本数p = int(n / q) # 特征数print(f"矩阵维度: {n} × {p}")max_eigenvals = []for trial in range(n_trials):# 生成随机矩阵(标准正态分布)X = np.random.randn(n, p)# 标准化X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)# 计算样本协方差矩阵S = X.T @ X / (n - 1)# 计算特征值eigenvals = np.linalg.eigvals(S)max_eigenvals.append(np.max(eigenvals))# 统计结果empirical_max = np.mean(max_eigenvals)theoretical_max = 1 + 1/q + 2/np.sqrt(q)print(f"经验最大特征值: {empirical_max:.4f} ± {np.std(max_eigenvals):.4f}")print(f"理论预测值: {theoretical_max:.4f}")print(f"相对误差: {abs(empirical_max - theoretical_max)/theoretical_max:.2%}")numerical_verification()

一般来说,我们使用aspect ratio计算出来lamda,我们只需要取其中的lamda_plus,也就是代码中计算出来的特征值上界,我们就可以直接取这个上界作为阈值,来选取我们所需要的显著的特征值了。
当然,实际降维的时候,我们所需要的特征值其实很少,可视化一般2个,PC1、PC2,
我们理论上可以按照自己分析需求(注意是个人分析需求),再在lamda_plus乘上一个缩放因子,也就是我前面代码中的变量clean_threshold,
然后这个缩放因子,如果是1的话,我就作为一般处理,并没有强化,所以我一般写函数的时候就是default=1
(4)基本的随机矩阵概念:特征值与奇异值
参考:https://www.math.pku.edu.cn/teachers/lidf/docs/statcomp/html/_statcompbook/matrix-eig.html
特征值的概念很好理解,方阵A对其特征向量α所做的变换,等效于其特征值lamda对其特征向量α所做的变换;
然后奇异值,在定义上,也是按照特征值分解的方式;
当然,奇异值和特征值还是有区别的:



在矩阵分析中,奇异值和特征值是两个不同的概念,但它们之间存在一定的联系。以下是结合全文内容对它们的解释和区别:
特征值(Eigenvalues)
- 定义:对于一个方阵 ( A ),如果存在一个非零向量 ( v ) 和一个标量 ( lambda ),使得 ( A v = lambda v ),则称 ( lambda ) 是矩阵 ( A ) 的特征值,( v ) 是对应的特征向量。
- 性质:
- 特征值是方阵的固有属性,反映了矩阵在特征向量方向上的“拉伸”或“压缩”程度。
- 特征值可以是实数或复数,取决于矩阵的性质。
- 对于对称矩阵,特征值总是实数,并且特征向量是正交的。
奇异值(Singular Values)
- 定义:对于任意矩阵 ( A )(不一定是方阵),其奇异值是矩阵 ( A^T A ) 的特征值的平方根。具体来说,如果 ( A ) 是一个 ( m x n ) 的矩阵,那么 ( A ) 的奇异值是矩阵 ( A^T A ) 的特征值的非负平方根。
- 性质:
- 奇异值总是非负的。
- 奇异值反映了矩阵在不同方向上的“伸展”程度,可以用于描述矩阵的“能量”分布。
- 对于任意矩阵 ( A ),其奇异值分解(SVD)可以表示为 ( A = U Sigma V^T ),其中 ( U ) 和 ( V ) 是正交矩阵,( Sigma ) 是对角矩阵,对角线上的元素是 ( A ) 的奇异值。
区别
- 适用范围:
- 特征值仅适用于方阵。
- 奇异值适用于任意形状的矩阵。
- 物理意义:
- 特征值描述的是矩阵在特征向量方向上的“拉伸”或“压缩”程度。
- 奇异值描述的是矩阵在不同方向上的“伸展”程度,可以用于描述矩阵的“能量”分布。
- 计算方式:
- 特征值是通过解特征方程 ( det(A - lambda I) = 0 ) 得到的。
- 奇异值是通过计算矩阵 ( A^T A ) 的特征值的平方根得到的。
(5)重构协方差矩阵
就是我前面代码中的这一块:

这一块其实是特征值分解的一些代数常识(手敲markdown解释如下):

这个操作其实是谱分解(Spectral Decomposition)的阶段版本,有几个重要的数学意义:

从理论上讲
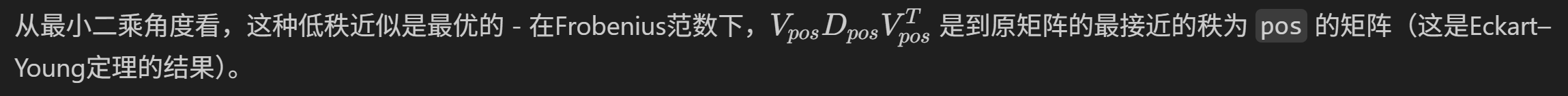
这个重构过程有效地滤除了数据中的噪声nosie部分,保留了主要的变异信息。
(6)计算主成分得分
然后是主成分得分:PC_scores

