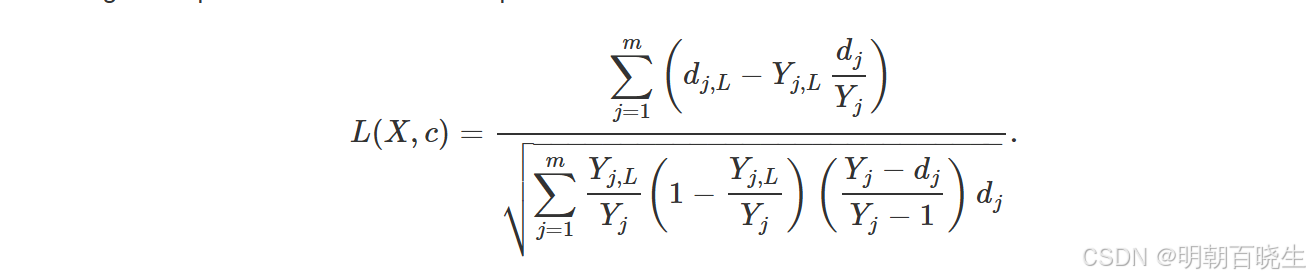当前位置：首页 > news >正文

临床医学 RANDOM SURVIVAL FORESTS（randomSurvivalForest）-2 python 例子

news 2025/8/9 14:07:57

接：临床医学 RANDOM SURVIVAL FORESTS（randomSurvivalForest）-1-CSDN博客

随机森林 (RF) 的早期应用侧重于回归和分类问题。随机生存森林(RSF) 的引入是为了将 RF 扩展到右删失生存数据的场景。RSF 的实现遵循与 RF 相同的一般原则：

使用引导数据生长生存树；
在拆分树节点时使用随机特征选择；
树通常生长得很深；
通过平均终端节点统计数据 (TNS terminal node statistics ) 来计算生存森林集成。

生存数据中存在删失是其独有的特征，这使得 RSF 的某些方面比用于回归和分类的 RF 复杂化。在右删失生存数据中，观测数据为 $(T,\delta )$ T是生存时间和 $\delta$ 是censoring indicator。

   $T= min(T^0,C^0)$

   $T^0$ 代表实际观察到的事件发生时间

   $C^0$ 代表删失时间

censoring indicator $\delta = I(T^0<C^0)$

当发生了一个事件（即发生了死亡）， $T=T^0$ , $\delta =1$ .我们观察到了真实的事件时间

否则 $T=C^0$ ， $\delta =0$ ，我们只观察删失时间，因此我们知道这个受试者存活下来，但当受试者真正死亡时则不会。

下文我们将数据表示为 $(T_1,X_1,\delta_1)$ ，… ， $(T_n,X_n,\delta_n)$

   $X_i$ 是特征向量（协变量）

   $T_i:$ 受试者的事件发生的事件

   $\delta_i$ : censoring indicators

RSF 树与 RF 树一样，都是通过重采样来生长的

临床医学 RANDOM SURVIVAL FORESTS（randomSurvivalForest）-1-CSDN博客Cox Proportional Hazards Model（PYTHON例子）_bootstrap validation of a cox proportional hazards-CSDN博客临床医学AI LogRank - Test-CSDN博客

Random Survival Forests • Fast Unified Random Forests with randomForestSRCCox Proportional Hazards Model（PYTHON例子）_bootstrap validation of a cox proportional hazards-CSDN博客

问题：样本量小的时候是否适合使用RSF

RSF分裂是基于Log-rank检验比较子节点间生存差异的卡方统计量

RSF splitting rules
estimator
Prediction error
C-index 计算 &python 例子
Brier score & python 例子
Variable Importance
讨论
python 例子

一 RSF splitting rules

在构建随机生存森林（RSF）树的过程中，必须处理真实事件时间存在删失（censoring）的情况。具体而言，用于生长树木的分裂准则需要特别考虑删失机制。其核心目标是将树节点分割为左、右子节点，使得两个子节点的事件历史（生存）行为存在显著差异。

（在跟临床医生沟通的过程中,他们观测到的censoring大部分为死亡，所以使用RSF 需要特别注意）

1.1 Log-rank splitting

在随机生存森林（RSF）的实现中，包默认采用的分裂规则是对数秩检验统计量（log-rank test statistic），并通过参数splitrule="logrank"指定。对数秩检验传统上用于生存数据的两组比较，但也可作为生存树的分裂准则，通过最大化节点间生存差异来实现有效分割[2–6]。

为解释对数秩分裂的具体机制，我们考虑一个待分割的特定树节点。不失一般性，假设该节点为根节点（树结构的顶层）。为简化讨论，假设数据未经过自助采样（bootstrapping），因此根节点包含的数据为 $(T_1,X_1,\delta_1),...(T_n,X_n,\delta_n)$ 。设X表示某一特定变量（即特征向量的某个坐标）。基于X的候选分割方式为X≤c和X>c（为简化讨论，假设X为标称型变量），该分割将当前节点划分为左子节点 $L=\begin{Bmatrix} X \leq c \end{Bmatrix}$ 和右子节点 $R=\begin{Bmatrix} X \geq c \end{Bmatrix}$ 。令

$t_1 < t_2 ...< t_m$

设 $t_j$ 为不同的死亡时间点

$d_{j,L}, d_{j,R}$ 分别表示在时间 $t_j$ 时，左右子节点L、R中的死亡人数

$Y_{j,L}, Y_{j,R}$ 分别表示在时间 $t_j$ 时，左右子节点L、R中的处于风险中的个体数。

定义

$d_j= d_{j,L}+d_{j,R}, Y_j =Y_{j,L}+Y_{j,R}$

基于变量X和分割点c的对数秩分裂统计量值为：

临床医学AI LogRank - Test_log-rank test-CSDN博客

这个公式跟logRank 统计用的原理是相同的，但是形式上有差异

∣L(X,c)∣的值是节点分离程度的度量。该值越大，表示左右子节点L和R之间的生存差异越显著，分裂效果越好。最佳分裂通过寻找特征变量 $X^*$ 和分割值 $C^*$ 来确定，使得对于所有特征变量X和分割值c，均有∣L( $X^*,C^*$ )∣≥∣L(X,c)∣

1.2 Log-rank score splitting

该软件包还实现了基于对数秩评分检验（log-rank score test）的分裂规则，可通过参数splitrule="logrankscore"指定。以下对该规则进行具体说明：

假设变量X已按升序排列，即 $X_1<X_2..<X_n$ ，为简化讨论，假设X的取值为n个唯一值（无重复值）。首先计算每个生存时间 $T_j$ 对应的"秩"值 $a_j$ ，其计算公式为：

式中，aˉ和sa2分别为序列{ $a_j$ :j=1,…,n}的样本均值和样本方差； $n=n_L+n_R$ ，其中 $n_L$ 为左子节点的样本量。对数秩评分分裂规则以∣S(X,c)∣作为节点分离程度的度量指标。通过最大化该值，可确定最优分裂特征 $X^*$ 和分裂阈值 $C^*$ ，即满足对所有X和c，均有∣S( $X^*,C^*$ )∣≥∣S(X,c)∣

这种思想参考： https://www.bilibili.com/video/BV1Aw411w7CG/?spm_id_from=333.337.search-card.all.click&vd_source=a624c4a1aea4b867c580cc82f03c1745

1.3 随机分割

包中的所有模型（包括随机生存森林，RSF）均支持通过选项nsplit指定的随机分割（randomized splitting）。其核心思想是：而非通过遍历变量的所有可能分割值来分割节点，而是选择固定数量的随机分割点c1,…,cnsplit[1, 8, 9]。例如，使用对数秩分割的最佳随机分割为∣L(X, $c_1$ )∣,…,∣L(X, $c_{nsplit}$ )∣中的最大值。

对于每个变量X，此方法将分割统计量的评估次数从最坏情况下的n次（传统确定性分割）减少至nsplit次。随机分割不仅显著降低了计算量，还缓解了树模型中已知的偏差问题——即传统方法倾向于选择具有大量分割点的变量（如连续变量或分类标签数量较多的因子变量）[10]。相关研究包括[11]，其探讨了极端随机树（extremely randomized trees），该方法为每个变量选择单一随机分割点（即nsplit=1）。传统确定性分割（遍历所有分割值）通过nsplit=0指定。

1.4 Terminal node statistics (TNS)

RSF 模型可以统计两个：

生存函数 $S(t|X)=P\begin{Bmatrix} T^0)>t|X \end{Bmatrix}$

累积风险函数（CHF）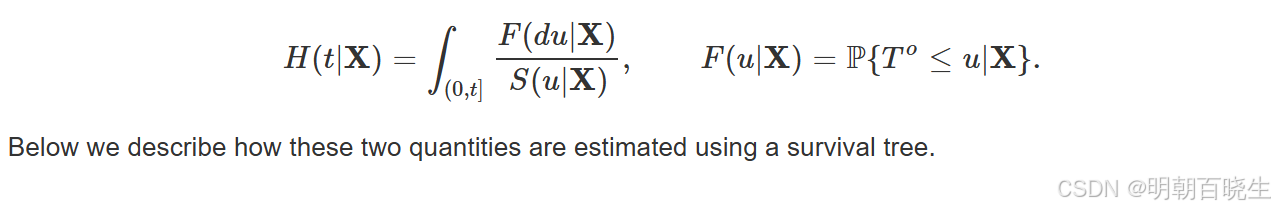

二 estimator

2.1 In-bag (IB) estimator

生存树构建完成后，树的末端被称为终端节点（ terminal nodes）。生存树预测器的定义基于每个终端节点内部的预测结果。设 h 为树的一个终端节点，令 $t_{1,h} <t_{2,h}<...<t_{m(h),h}$ ,h 为节点 h 中的唯一死亡时间点， $d_{j,h}$ 和 $Y_{j,h}$ 分别表示在时间 $t_{j,h}$ 时的死亡人数和处于风险中的个体数。节点 h 的累积风险函数（CHF）和生存函数通过基于自助法的Nelson-Aalen和Kaplan-Meier估计器进行估计：

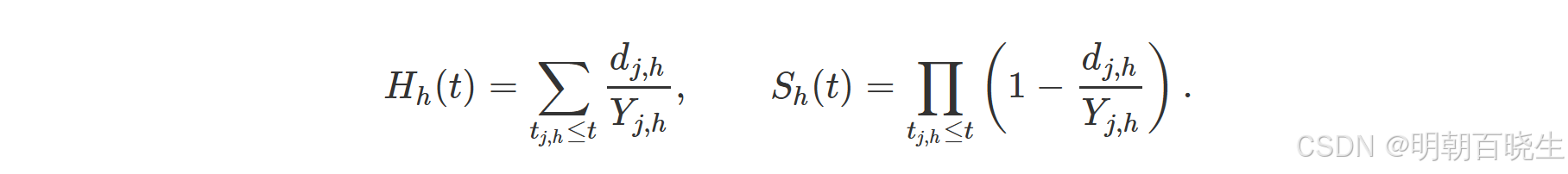
生存树预测器的定义是：

为节点 h 内的所有样本赋予相同的CHF和生存估计值。这是因为生存树的目的是将数据划分为具有相似生存行为的同质组（即终端节点）。

对于给定特征 X，其累积风险函数 $H(t|X)$ 和生存函数 $s(t|X)$ 的估计方法如下：

将 X 输入生存树，由于树的二分特性，X 会落入唯一的终端节点 h。

此时，X 的CHF和生存估计值等于其所属终端节点 h 的Nelson-Aalen和Kaplan-Meier估计值：

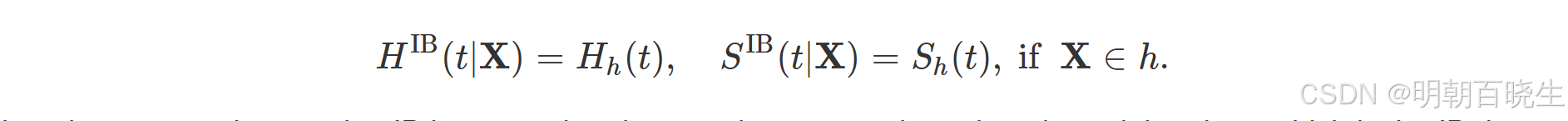
注：我们使用“IB”符号是因为上述估计器基于训练数据（即袋内数据）。

2.2 Out-of-bag (OOB) estimators

为定义袋外估计器，设 $I_i$ ∈{0,1} 表示样本 i 是否为袋内（IB）或袋外（OOB）数据。当且仅当 $I_i=1$ 时，样本 i 为袋外数据。将样本 i 输入生存树，设其落入终端节点 h。则样本 i 的袋外树估计器为：

2.3 Ensemble CHF and Survival Function

集成模型的累积风险函数（CHF）和生存函数通过对单棵树的估计量取平均得到。设 $H_b^{IB}(t|X)$ 和 $S_{b}^{IB}(t|X)$ 分别为第 b 棵生存树的袋内（IB）CHF和生存估计量，则袋内集成估计器定义为：

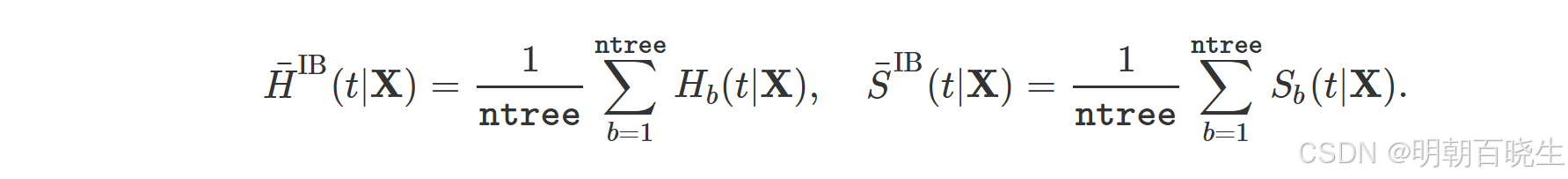
其中 ntree 为生存树的数量。

对于袋外（OOB）估计器，设 $O_i$ 记录样本 i 为袋外数据的树集合（即样本 i 未参与这些树的构建）。样本 i 的袋外集成估计器为：

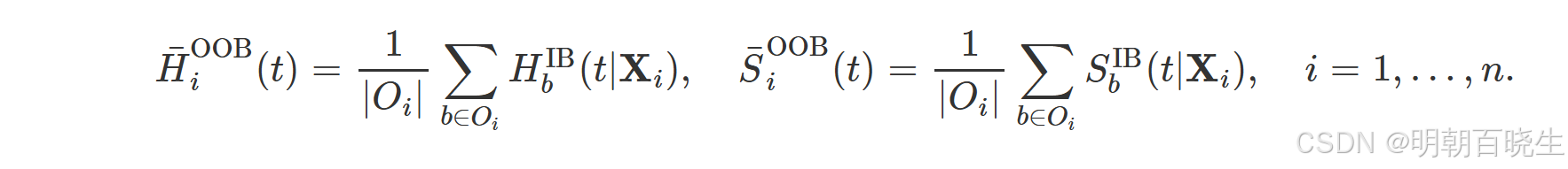
其中 ∣Oi∣ 表示样本 i 为袋外数据的树的数量

2.4 为何需要同时估计CHF和生存函数？

随机生存森林（RSF）同时提供累积风险函数（CHF）H(t∣X) 和生存函数 S(t∣X) 的估计，原因在于集成模型中两者的数学关系不再严格成立。传统上，CHF与生存函数足

$H(t)=-log(S(t))$ (coxPH 模型中有讲解, YouTu是通过求导后的映射关系）

但在集成框架下，这一等式可能被打破。

关键原因：Jensen不等式的影响

设 $S_b(t)$ 和 $H_b(t)$ 分别为第 b 棵树的生存函数和CHF估计量。对于单棵树，等式 $H_b(t)=-log S_b(t)$ 成立。然而，当对多棵树取平均得到集成估计量时：

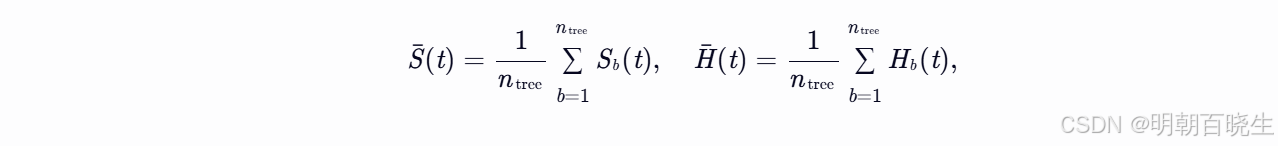
根据Jensen不等式（针对凸函数 f(x)=−log(x)）：函数的期望小于期望的函数

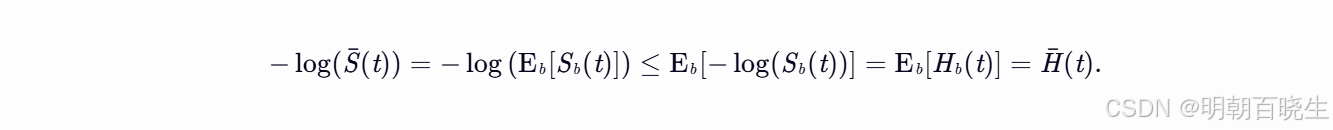
这表明：对生存函数取平均后再取负对数，结果会小于或等于CHF的平均值。因此两者不再严格等价。

实际应用中的意义

避免估计偏差：若仅通过 Sˉ(t) 推导 Hˉ(t)，会因Jensen不等式导致 Hˉ(t) 被低估。分别估计可确保两者的准确性。
满足不同分析需求：
- 生存函数 S(t∣X) 用于预测个体在时间 t 的生存概率；
- CHF H(t∣X) 用于分析累积风险，例如计算风险比或构建风险预测模型。

三 Prediction error

3.1 死亡率（RSF使用的预测值）

为计算一致指数（C-index），需明确何为“更差的预测结果”。对于生存模型，这由死亡率（mortality）定义，它是RSF使用的预测值。设 $t_1<t_2<...<t_m$ 为训练数据中所有唯一的事件时间点。特征 X 的袋内（IB）集成死亡率定义为：

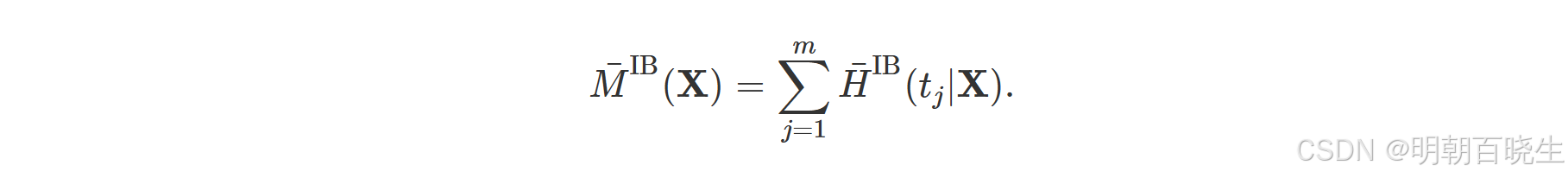
该值估计了“若所有样本均与 X 特征相同，预期发生的事件数”。

用于计算C-index的袋外（OOB）集成死亡率定义为：

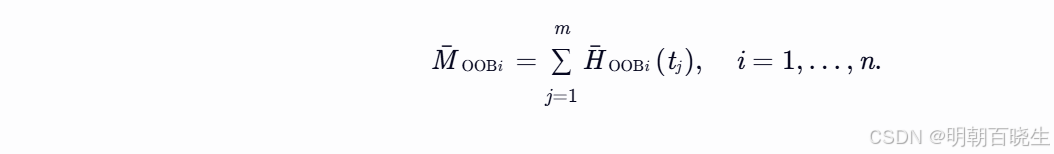
个体 i 的预后被认为比个体 j 更差，当且仅当：

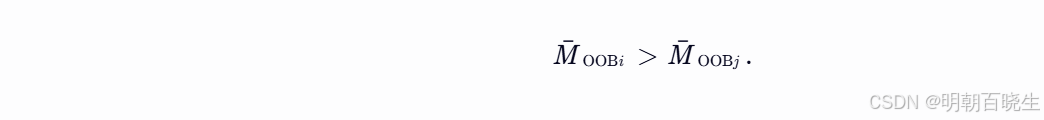
死亡率的意义
死亡率值[1]代表每个个体的估计风险，其尺度校准为事件数量。例如：若个体 i 的死亡率为100，则表示“若所有个体均具有与 i 相同的协变量 $X=X_i$ ，预期平均发生100起事件

四 C-index 计算

一致指数（C-index）的计算步骤

一致指数（C-index）通过以下步骤计算：

构建所有观测对
在全体数据中形成所有可能的观测对 (i,j)。
排除无效对
- 排除较短事件时间为删失（censored）的观测对。
- 排除满足的观测对，除非以下条件之一成立：
  - $\delta_i=1,\delta_j=0$ ：i 为事件，j 为删失；
  - $\delta_i=0 ,\delta_j=1$ ：i 为删失，j 为事件；
  - $\delta_i=1 ,\delta_j=1$ ：两者均为事件
- 剩余有效对记为集合 S，其数量为 ∣S∣=permissible。
计数规则
- 当 $T_i=T_j$ 时：
  - 若较短时间对应的个体预后更差（即 $M_{oob_i}>M_{oob_j}$ ），计1分；
  - 若预后相同（ $M_{oob_i}=M_{oob_j}$ ），计0.5分。
- 当 $T_i=T_j$ 时：
  - 若预后相同（ $M_{oob_i}=M_{oob_j}$ ），计1分；
  - 若预后不同（ $M_{oob_i} \neq M_{oob_j}$ ），计0.5分。
计算一致指数
将所有有效对的得分求和，得到一致计数（concordance）。一致指数 C 定义为：

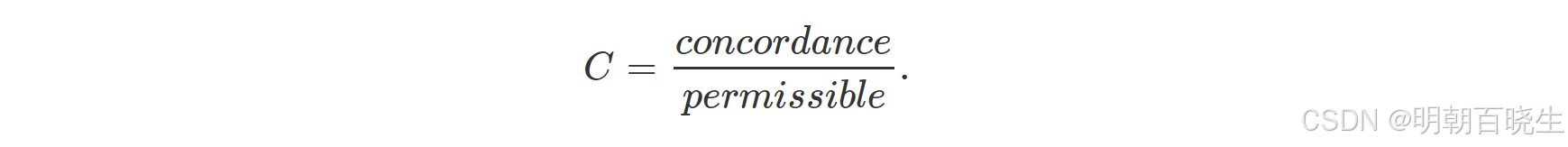
错误率 PE=1−C。需注意：

0≤PE≤1；
PE=0.5 表示模型预测效果与随机猜测无异；
PE=0 表示完美预测。

import numpy as npdef calculate_c_index(event_time, event_status, risk_score):"""Calculate the C-index (concordance index) for survival analysis.Parameters:event_time (np.ndarray): Array of observed event/censoring timesevent_status (np.ndarray): Array of event indicators (1: event, 0: censored)risk_score (np.ndarray): Array of predicted risk scores (higher = more risky)Returns:float: C-index value between 0 and 1"""n = len(event_time)permissible_pairs = 0concordant_count = 0.0# Iterate over all possible pairsfor i in range(n):for j in range(i + 1, n):time_i = event_time[i]time_j = event_time[j]status_i = event_status[i] # censoring indicatorstatus_j = event_status[j] #  censoring indicatorrisk_i = risk_score[i]risk_j = risk_score[j]# Determine observed time and event status for comparisonif time_i < time_j:shorter_time = time_ilonger_time = time_jshorter_status = status_ilonger_status = status_jelif time_i > time_j:shorter_time = time_jlonger_time = time_ishorter_status = status_jlonger_status = status_ielse:  # Equal timesshorter_time = time_ilonger_time = time_jshorter_status = status_ilonger_status = status_j# Skip pairs where shorter time is censoredif shorter_time < longer_time and shorter_status == 0:continue# Handle ties in event timesif shorter_time == longer_time:# Skip if both censored or both events with no valid comparisonif (shorter_status == 0 and longer_status == 0) :continue# Count this as a permissible pairpermissible_pairs += 1# Case 1: Different event timesif shorter_time != longer_time:if shorter_time == time_i:  # i has shorter timeif risk_i > risk_j:concordant_count += 1elif risk_i == risk_j:concordant_count += 0.5else:  # j has shorter timeif risk_j > risk_i:concordant_count += 1elif risk_j == risk_i:concordant_count += 0.5# Case 2: Equal event timeselse:if risk_i == risk_j:concordant_count += 1else:concordant_count += 0.5# Avoid division by zeroif permissible_pairs == 0:return 0.0c_index = concordant_count / permissible_pairsreturn c_index# Example usage
if __name__ == "__main__":event_times =    np.array([5, 6, 7, 8, 9])event_statuses = np.array([1, 0, 1, 1, 0])risk_scores =    np.array([5.5, 4.8, 3.0, 2.9, 1.2])# Calculate C-indexc_index = calculate_c_index(event_times, event_statuses, risk_scores)prediction_error = 1 - c_indexprint(f"C-index: {c_index:.4f}")print(f"Prediction error (1-C): {prediction_error:.4f}")

五 Brier score

Brier得分是评估预测性能的另一常用指标。设 $\hat S \bigl(\begin{smallmatrix} t|X \end{smallmatrix}\bigr)$ 为生存函数的某个估计器， $\hat G \bigl(\begin{smallmatrix} t|X \end{smallmatrix}\bigr)$ 为预先选定的删失生存函数估计器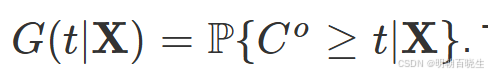，其中 C0 为删失时间）。通过逆概率删失加权（IPCW）方法[13]， $\hat S \bigl(\begin{smallmatrix} t|X \end{smallmatrix}\bigr)$ 的Brier得分可估计为：

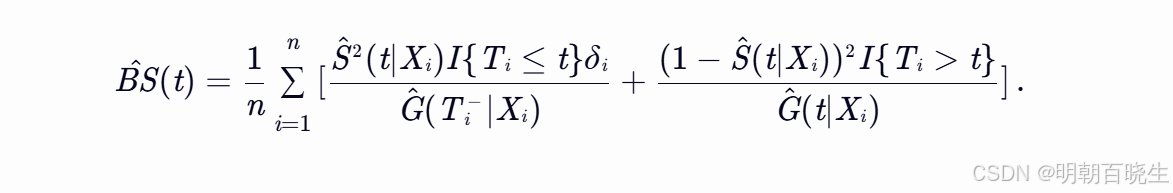
在时间 τ 处的集成Brier得分（IBS）定义为：

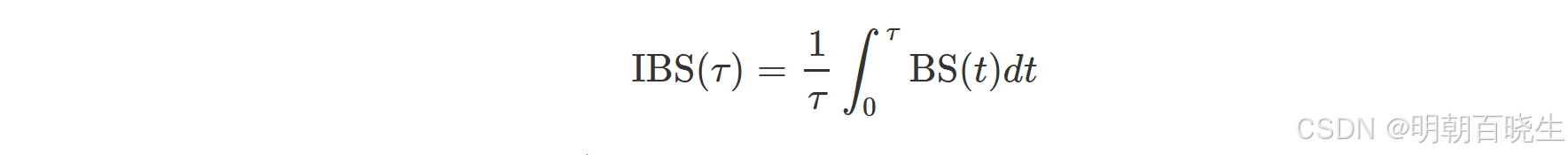
可通过将 BS(t) 替换为其估计值 BS^(t) 进行计算。Brier得分越低，表示预测性能越好。

进一步，可通过集成Brier得分定义连续排名概率得分（CRPS），其计算方式为集成Brier得分除以时间：

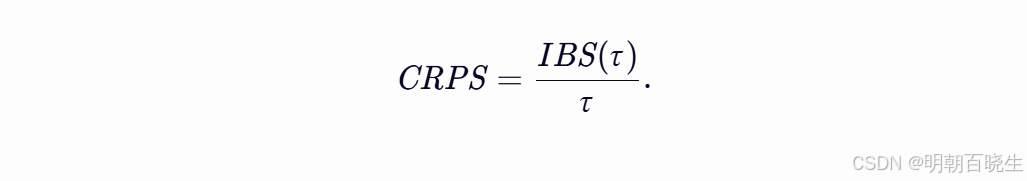
import numpy as np
from typing import Callable, Tupledef kaplan_meier_survival(times: np.ndarray, events: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:"""使用Kaplan-Meier方法估计生存函数参数:times: 观测时间数组 (包括事件时间和删失时间)events: 事件指示数组 (1=事件发生, 0=删失)返回:unique_times: 唯一事件时间点 (升序排列)survival_probs: 对应时间点的生存概率"""# 按时间排序sorted_indices = np.argsort(times)sorted_times = times[sorted_indices]sorted_events = events[sorted_indices]# 获取唯一事件时间点unique_times = np.unique(sorted_times[sorted_events == 1])# 初始化生存概率n_obs = len(times)survival_probs = np.ones(len(unique_times) + 1)  # 包含时间0# 在时间0处生存概率为1unique_times = np.insert(unique_times, 0, 0)risk_set = n_obs  # 初始风险集大小cum_survival = 1.0  # 累积生存概率# 计算每个时间点的生存概率for i in range(1, len(unique_times)):time = unique_times[i]# 计算当前时间点发生的事件数events_at_time = np.sum((sorted_times == time) & (sorted_events == 1))# 计算当前时间点的风险集大小risk_set = np.sum(sorted_times >= time)# 计算生存概率survival_prob = 1 - events_at_time / risk_setcum_survival *= survival_probsurvival_probs[i] = cum_survivalreturn unique_times, survival_probsdef left_continuous_survival_function(unique_times: np.ndarray, survival_probs: np.ndarray) -> Callable[[float], float]:"""创建左连续生存函数参数:unique_times: 唯一时间点数组survival_probs: 对应生存概率数组返回:函数: 输入时间t，返回左连续的生存概率"""def survival_func(t: float) -> float:# 对于t小于最小时间点的情况if t < unique_times[0]:return 1.0# 对于t大于最大时间点的情况if t >= unique_times[-1]:return survival_probs[-1]# 找到小于t的最大时间点索引idx = np.searchsorted(unique_times, t, side='right') - 1return survival_probs[idx]return survival_funcdef brier_score(t: float, times: np.ndarray, events: np.ndarray, pred_survival: np.ndarray, censoring_survival_func: Callable[[float], float]) -> float:"""计算给定时间点t的Brier得分参数:t: 评估时间点times: 观测时间数组events: 事件指示数组 (1=事件, 0=删失)pred_survival: 预测的生存概率数组 (在时间t)censoring_survival_func: 删失生存函数返回:Brier得分 (标量)"""n = len(times)total_score = 0.0for i in range(n):time_i = times[i]event_i = events[i]pred_i = pred_survival[i]# 计算删失分布权重if time_i < t and event_i == 1:# 事件发生在t之前：使用事件时间之前的删失生存概率weight = censoring_survival_func(time_i)term = (0 - pred_i) ** 2elif time_i > t:# 观测时间超过t：使用时间t的删失生存概率weight = censoring_survival_func(t)term = (1 - pred_i) ** 2else:# 其他情况不贡献得分continue# 避免除零错误if weight < 1e-10:continuetotal_score += term / weightreturn total_score / ndef integrated_brier_score(tau: float, times: np.ndarray, events: np.ndarray, pred_survival_func: Callable[[float], np.ndarray],num_points: int = 100) -> float:"""计算集成Brier得分(IBS)和连续排名概率得分(CRPS)参数:tau: 评估时间上限times: 观测时间数组events: 事件指示数组 (1=事件, 0=删失)pred_survival_func: 预测生存函数 (输入时间t，返回生存概率数组)num_points: 积分点数返回:ibs: 集成Brier得分crps: 连续排名概率得分"""# 估计删失生存函数 (使用Kaplan-Meier)# 注意：删失分布的事件指示为1-events (删失发生视为事件)censoring_events = 1 - eventsunique_times, censoring_probs = kaplan_meier_survival(times, censoring_events)censoring_survival = left_continuous_survival_function(unique_times, censoring_probs)# 创建时间网格用于积分time_grid = np.linspace(0, tau, num_points)brier_scores = np.zeros(num_points)# 计算每个时间点的Brier得分for i, t in enumerate(time_grid):# 获取在时间t的预测生存概率pred_survival = pred_survival_func(t)brier_scores[i] = brier_score(t, times, events, pred_survival, censoring_survival)# 使用梯形法则进行数值积分ibs = np.trapz(brier_scores, time_grid) / tau# 计算连续排名概率得分 (CRPS)crps = ibs / taureturn ibs, crps# 示例使用
if __name__ == "__main__":# 设置随机种子确保可重复性np.random.seed(42)# 生成模拟数据n_samples = 100observation_times = np.random.exponential(scale=10, size=n_samples)event_indicators = np.random.binomial(1, 0.7, size=n_samples)  # 70%事件率# 创建预测生存函数 (这里使用简单的指数模型作为示例)# 实际应用中应由生存分析模型提供def predicted_survival_func(t: float) -> np.ndarray:# 简化示例：假设风险分数与时间成正比risk_scores = observation_times / 10return np.exp(-t * np.exp(risk_scores))# 设置评估时间上限tau = np.max(observation_times[event_indicators == 1])  # 使用最大事件时间print(f"设置评估时间上限{tau}")# 计算集成Brier得分和CRPSibs, crps = integrated_brier_score(tau=tau,times=observation_times,events=event_indicators,pred_survival_func=predicted_survival_func,num_points=50)# 输出结果print(f"集成Brier得分 (IBS): {ibs:.4f}")print(f"连续排名概率得分 (CRPS): {crps:.4f}")

六 变量重要性（Variable Importance）

随机生存森林（RSF）提供了一种完全非参数的变量重要性（VIMP）度量方法。最常用的指标是Breiman-Cutler VIMP[15]，称为排列重要性（permutation importance）。基于排列重要性的VIMP计算采用预测误差增量法，通过衡量变量对预测误差的贡献来评估其重要性。其巧妙之处在于，未采用计算成本较高的交叉验证，而是利用袋外（OOB）估计。具体步骤如下：

单变量重要性计算：
对变量 X，随机打乱其袋外数据中的值（保持其他变量不变），将扰动后的袋外数据输入树模型，计算新的袋外误差。
树重要性度量：
新误差与原始袋外误差的差值，即为变量 X 在该树中的重要性。（跟SHAP 计算过程相似）
集成重要性：
对所有树的结果取平均，得到变量 X 的排列重要性。

结果解读：

高正值：表示变量具有强预测能力；
零或负值：可能为噪声变量（无预测价值）。

统计推断：
可通过子采样（subsampling）[16]估计VIMP的标准误，并构建近似置信区间。图3展示了收缩期心力衰竭RSF分析中，p=39 个变量的删除-d jackknife 99%渐进正态置信区间（预测误差通过C-index计算）

七 . 论文讨论

本文介绍了随机生存森林（RSF），这是Breiman随机森林方法[Breiman, 2001]在右删失生存数据中的新扩展。随机生存森林由随机生存树组成：通过独立自助法样本构建每棵树，在每个节点随机选择变量子集，并基于涉及生存时间和删失状态信息的生存准则进行节点分裂。当每个终端节点的唯一死亡数不少于预设阈值d0>0时，认为树已完全生长。案例的估计累积风险函数（CHF）是其终端节点的Nelson-Aalen估计量，集合模型是所有终端节点CHF的平均值。由于树由袋内数据生长而成，可通过将袋外案例下推至其对应的袋内生存树并取平均值，计算袋外集合模型。使用袋外集合模型预测案例时，不依赖该案例的生存信息，因此可用于几乎无偏的预测误差估计。由此可进一步推导出其他有用指标，例如用于变量筛选和选择的VIMP（变量重要性）值。

RSF融合了Breiman（2001）提出的诸多核心思想，同时我们提出了扩展该方法的新途径。例如，引入了一种新颖的缺失数据算法，该算法适用于训练和测试数据，即使存在大量缺失数据，也能提供几乎无偏的误差率估计。

通过一项大型实验评估了RSF的预测准确性。在广泛的真实和模拟数据集上，RSF始终优于或至少不逊于其他竞争方法。自随机森林（RF）引入机器学习领域以来，已有大量工作验证其实证性能。我们的结果证实了普遍结论：RF能生成高度准确的集合预测器。

我们还展示了RSF在实际数据环境中的易用性：其可轻松揭示变量间高度复杂的相互关系。例如，在冠状动脉疾病的案例研究中，RSF发现了肾功能、体重指数与长期生存之间的重要关联，这有助于解释该争议话题文献中报道的诸多困惑。此类复杂关系可通过VIMP等工具结合森林的高度适应性轻松揭示。相比之下，传统方法的自动化程度较低，在变量高度相关的数据环境中，需要用户提供大量主观输入

八 Python 例子

#!/usr/bin/env python
# -*- coding: utf-8 -*-"""
随机生存森林(RSF)在医学研究中的应用示例本脚本演示如何使用随机生存森林(RSF)分析生存数据，包括：
1. 模拟生成生存数据集
2. 训练RSF模型
3. 评估模型性能(C-index)
4. 计算特征重要性
5. 预测患者生存曲线
6. 计算集成死亡率
7. 与传统Cox模型比较
8. 模型校准评估作者: [chengxf]
机构: [Lenovo]
日期: [2025]
"""import numpy as np
import matplotlib.pyplot as plt
from sksurv.ensemble import RandomSurvivalForest
from sksurv.metrics import concordance_index_censored
from sksurv.linear_model import CoxPHSurvivalAnalysis
from sklearn.model_selection import train_test_split
from sklearn.inspection import permutation_importance
import warnings# 忽略特定警告，避免干扰输出
warnings.filterwarnings("ignore", category=UserWarning)# 设置全局随机种子确保结果可重现
np.random.seed(42)# 1. 创建模拟生存数据集
def generate_survival_data(n_samples=100, random_seed=None):"""生成模拟生存数据集，用于生存分析研究参数:n_samples (int): 样本数量，默认为100random_seed (int): 随机种子，确保结果可重现返回:X (np.ndarray): 特征矩阵 (n_samples, n_features)y (np.array): 生存数据，结构化数组，包含事件和时间特征说明:- 特征0: 年龄 (指数分布，模拟偏态分布)- 特征1: 肿瘤大小 (正态分布，均值为3.5cm)- 特征2: 治疗方案 (0=常规治疗, 1=实验治疗)"""# 特征矩阵: 年龄、肿瘤大小、治疗方案X = np.column_stack((np.random.exponential(scale=50, size=n_samples),  # 年龄 (指数分布模拟偏态)np.random.normal(loc=3.5, scale=1.0, size=n_samples),  # 肿瘤大小(cm)np.random.choice([0, 1], size=n_samples)  # 治疗方案 (二元分类)))# 生成风险评分: 线性组合特征# 系数设置: 年龄(0.1), 肿瘤大小(0.5), 治疗方案(-0.8)risk_scores = 0.1 * X[:, 0] + 0.5 * X[:, 1] - 0.8 * X[:, 2]# 生成生存时间: 指数风险模型survival_time = np.exp(2.5 - 0.3 * risk_scores + np.random.normal(scale=0.5, size=n_samples))# 添加随机删失 (约30%的数据)censored = np.random.binomial(1, 0.3, size=n_samples)  # 1表示删失，0表示事件observed_time = np.where(censored == 1,survival_time * np.random.uniform(0.1, 0.8, size=n_samples),  # 删失时间survival_time  # 事件时间)# 创建结构化数组 (scikit-survival要求格式)# dtype说明: 'event' (bool) - 是否观察到事件; 'time' (float) - 观察时间y = np.empty(n_samples, dtype=[('event', bool), ('time', float)])y['event'] = censored == 0  # True=观察到事件(死亡)，False=删失(未观察到事件)y['time'] = observed_timereturn X, y# 2. 生成数据集 (100个样本)
print("正在生成模拟生存数据集...")
X, y = generate_survival_data(n_samples=100)
print(f"数据集生成完成: {X.shape[0]}个样本, {X.shape[1]}个特征")# 3. 分割数据集为训练集和测试集
print("\n分割数据集 (80%训练, 20%测试)...")
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,  # 20%作为测试集stratify=y['event'],  # 按事件状态分层抽样random_state=42  # 固定随机状态确保可重现
)# 输出数据集统计信息
n_train_events = np.sum(y_train['event'])
n_test_events = np.sum(y_test['event'])
print(f"训练集: {len(y_train)}样本, 事件数: {n_train_events}")
print(f"测试集: {len(y_test)}样本, 事件数: {n_test_events}")# 4. 训练随机生存森林(RSF)模型
print("\n训练随机生存森林模型...")
rsf = RandomSurvivalForest(n_estimators=100,        # 树的数量 (增加可提高稳定性但增加计算时间)min_samples_split=10,     # 节点分裂最小样本数 (防止过拟合)min_samples_leaf=5,       # 叶节点最小样本数 (控制树复杂度)max_features="sqrt",      # 每棵树考虑的特征数 (sqrt(n_features)是常用设置)max_depth=None,           # 树的最大深度 (None表示不限制)n_jobs=-1,               # 使用所有CPU核心并行计算random_state=42,          # 固定随机状态确保可重现verbose=0                 # 不输出训练过程信息
)# 训练模型
rsf.fit(X_train, y_train)
print("RSF模型训练完成")# 5. 计算C-index (一致性指数)
def calculate_cindex(model, X, y):"""计算C-index (一致性指数)，评估模型区分能力参数:model: 训练好的生存模型X: 特征矩阵y: 生存数据 (结构化数组)返回:cindex (float): 一致性指数 (0.5-1.0)C-index解释:- 0.5: 随机猜测- >0.7: 模型具有较好区分能力- >0.8: 模型具有优秀区分能力"""# 预测风险评分 (风险评分越高，事件发生风险越高)pred_risk = model.predict(X)# 计算C-indexresult = concordance_index_censored(event_indicator=y['event'],  # 事件指示器 (True=事件发生)event_time=y['time'],        # 观察时间estimate=pred_risk           # 模型预测的风险评分)return result[0]  # 返回C-index值# 计算训练集和测试集C-index
print("\n评估模型性能 (C-index)...")
cindex_train = calculate_cindex(rsf, X_train, y_train)
cindex_test = calculate_cindex(rsf, X_test, y_test)print(f"训练集C-index: {cindex_train:.4f} (模型对训练数据的区分能力)")
print(f"测试集C-index: {cindex_test:.4f} (模型对未见数据的泛化能力)")# 6. 计算特征重要性 (使用排列重要性方法)
print("\n计算特征排列重要性...")
# 使用排列重要性评估特征贡献度
result = permutation_importance(estimator=rsf,           # 训练好的模型X=X_test,                # 测试集特征y=y_test,                # 测试集生存数据n_repeats=10,            # 重复次数 (增加可提高稳定性)random_state=42,         # 固定随机状态n_jobs=-1                # 并行计算
)# 特征名称 (对应数据集中的特征)
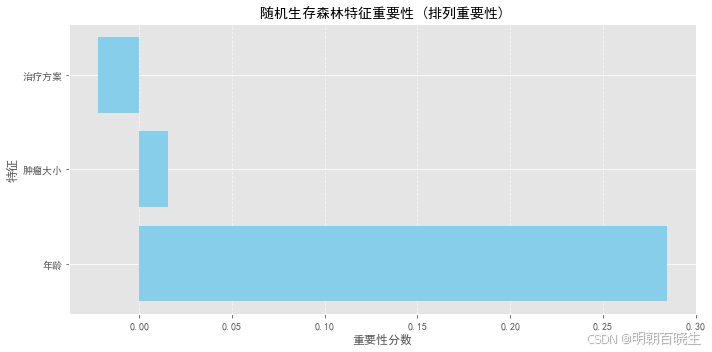
feature_names = ["年龄", "肿瘤大小", "治疗方案"]
importances = result.importances_mean  # 平均重要性分数# 可视化特征重要性
plt.figure(figsize=(10, 5))
plt.barh(feature_names, importances, color='skyblue')
plt.title("随机生存森林特征重要性 (排列重要性)", fontsize=14)
plt.xlabel("重要性分数", fontsize=12)
plt.ylabel("特征", fontsize=12)
plt.grid(axis='x', linestyle='--', alpha=0.7)
plt.tight_layout()
plt.savefig('feature_importance.png', dpi=300)  # 保存高分辨率图片
plt.show()print("特征重要性:")
for name, imp in zip(feature_names, importances):print(f"- {name}: {imp:.4f}")# 7. 模型解释：预测新患者生存曲线
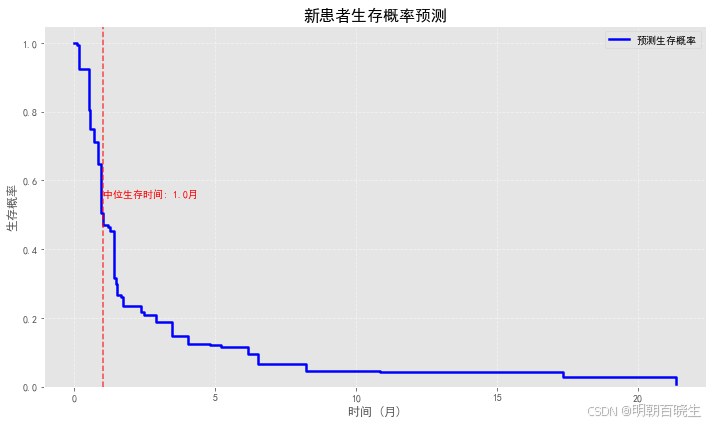
print("\n预测新患者生存曲线...")
# 新患者特征: [年龄, 肿瘤大小, 治疗方案]
new_patient = np.array([[65, 4.2, 1]])  # 65岁，肿瘤4.2cm，实验组治疗# 预测生存函数 (兼容不同scikit-survival版本)
try:# 新版本方法 (返回数组)surv_probs = rsf.predict_survival_function(new_patient, return_array=True)event_times = rsf.event_times_  # 事件时间点
except (TypeError, AttributeError):# 旧版本兼容方法surv_func = rsf.predict_survival_function(new_patient)event_times = surv_func[0].x  # 从生存函数对象获取时间点surv_probs = np.array([fn(event_times) for fn in surv_func])# 绘制生存曲线
plt.figure(figsize=(10, 6))
plt.step(event_times, surv_probs[0], where="post", color='b', linewidth=2.5, label='预测生存概率')# 添加关键时间点标记
median_surv_time = event_times[np.argmax(surv_probs[0] <= 0.5)]
plt.axvline(x=median_surv_time, color='r', linestyle='--', alpha=0.7)
plt.text(median_surv_time, 0.55, f'中位生存时间: {median_surv_time:.1f}月', fontsize=10, color='r')# 设置图表属性
plt.title("新患者生存概率预测", fontsize=16)
plt.xlabel("时间 (月)", fontsize=12)
plt.ylabel("生存概率", fontsize=12)
plt.ylim(0, 1.05)
plt.grid(True, linestyle='--', alpha=0.5)
plt.legend(loc='upper right')
plt.tight_layout()
plt.savefig('survival_curve.png', dpi=300)  # 保存高分辨率图片
plt.show()print(f"中位生存时间预测: {median_surv_time:.1f}月")# 8. 计算集成死亡率 (Ensemble Mortality)
def calculate_ensemble_mortality(model, X):"""计算集成死亡率 (Ensemble Mortality)集成死亡率定义为:M_i = Σ_{j=1}^{n} H_e(T_j | x_i)其中 H_e 是集成累积风险函数参数:model: 训练好的RSF模型X: 单个或多个患者的特征返回:mortality (float): 集成死亡率分数解释:集成死亡率是一个综合风险评分，值越高表示总体死亡风险越高在研究中用于比较不同患者的相对风险"""try:# 首选方法: 直接预测累积风险函数cum_hazard = model.predict_cumulative_hazard_function(X, return_array=True)return np.sum(cum_hazard, axis=1)except (NotImplementedError, AttributeError):try:# 备选方法: 通过生存函数计算累积风险surv_probs = model.predict_survival_function(X, return_array=True)# 累积风险 H(t) = -log(S(t))cum_hazard = -np.log(surv_probs + 1e-10)  # 添加小常数避免log(0)return np.sum(cum_hazard, axis=1)except (TypeError, AttributeError):# 旧版本兼容方法 (效率较低)surv_func = model.predict_survival_function(X)cum_hazard = np.zeros(len(X))# 获取事件时间点if 'event_times' in globals():times = event_timeselse:times = surv_func[0].xfor i, funcs in enumerate(surv_func):for t in times:s = funcs(t)  # 时间点t的生存概率cum_hazard[i] += -np.log(s + 1e-10)return cum_hazard# 计算新患者的集成死亡率
print("\n计算新患者集成死亡率...")
ensemble_mortality = calculate_ensemble_mortality(rsf, new_patient)
print(f"新患者集成死亡率: {ensemble_mortality[0]:.4f}")# 9. 与传统Cox比例风险模型比较
print("\n与传统Cox比例风险模型比较...")
# 训练Cox模型
cox = CoxPHSurvivalAnalysis()
cox.fit(X_train, y_train)# 计算Cox模型的C-index
cox_train_cindex = calculate_cindex(cox, X_train, y_train)
cox_test_cindex = calculate_cindex(cox, X_test, y_test)# 输出比较结果
print("模型性能比较 (C-index):")
print(f"             训练集      测试集")
print(f"RSF模型:    {cindex_train:.4f}     {cindex_test:.4f}")
print(f"Cox模型:    {cox_train_cindex:.4f}     {cox_test_cindex:.4f}")# 10. 模型校准评估
def plot_calibration(model, X, y, title, save_path=None):"""绘制模型校准曲线，评估预测风险与实际事件率的一致性参数:model: 训练好的生存模型X: 特征矩阵y: 生存数据title: 图表标题save_path: 图片保存路径 (可选)"""# 预测风险评分pred_risk = model.predict(X)# 按预测风险分组 (5组)groups = np.array_split(np.argsort(pred_risk), 5)actual_rates = []  # 实际事件率predicted_risks = []  # 平均预测风险for group in groups:# 计算组内实际事件率actual_rate = np.mean(y[group]['event'])# 计算组内平均预测风险predicted_risk = np.mean(pred_risk[group])actual_rates.append(actual_rate)predicted_risks.append(predicted_risk)# 绘制校准曲线plt.figure(figsize=(8, 6))plt.plot(predicted_risks, actual_rates, 'o-', markersize=8, linewidth=2, label='模型校准')plt.plot([0, 1], [0, 1], 'k--', linewidth=1.5, label='理想校准')# 设置图表属性plt.title(title, fontsize=14)plt.xlabel('预测风险', fontsize=12)plt.ylabel('实际事件率', fontsize=12)plt.legend(loc='best')plt.grid(True, linestyle='--', alpha=0.5)plt.tight_layout()# 添加R²值from scipy.stats import linregressslope, intercept, r_value, p_value, std_err = linregress(predicted_risks, actual_rates)plt.text(0.05, 0.9, f'R² = {r_value**2:.3f}', transform=plt.gca().transAxes)# 保存图片if save_path:plt.savefig(save_path, dpi=300)plt.show()# 绘制校准曲线
print("\n评估模型校准...")
plot_calibration(rsf, X_test, y_test, "RSF模型校准曲线 (测试集)",save_path='rsf_calibration.png')plot_calibration(cox, X_test, y_test, "Cox模型校准曲线 (测试集)",save_path='cox_calibration.png')print("分析完成")

参考：

临床医学AI LogRank - Test-CSDN博客

临床医学 RANDOM SURVIVAL FORESTS（randomSurvivalForest）-1-CSDN博客

Cox Proportional Hazards Model（PYTHON例子）_bootstrap validation of a cox proportional hazards-CSDN博客

Random Survival Forests • Fast Unified Random Forests with randomForestSRC

Cox Proportional Hazards Model（PYTHON例子）_bootstrap validation of a cox proportional hazards-CSDN博客

查看全文

http://www.dtcms.com/a/322010.html