nflsoi 8.8 题解

感觉这把难，不过今天状态比较差，头昏昏的。怎么后面几道蓝题别人光速切掉了？不过赛后再来看感觉也不算特别麻烦的题目。

C.#11698 双循环锦标赛 / TopCoder 10687 The Basketball Div One

题意

约翰与布鲁斯对团体体育赛事颇有研究，他们正在分析一场篮球锦标赛。

本次锦标赛共有n支参赛队伍，每两支队伍将进行两场对决（主客场各一场），每场比赛必有胜负，不存在平局。赛事结束后：

• 胜场数最多的队伍获得第1名；
• 胜场数次多的队伍获得第2名；
• ……
• 以此类推确定所有名次。

若存在某种赛事结果，使得第 $i$ 名队伍恰好获得 $W_i$ 场胜利，则称整数序列 $W_1,W_2,...,W_n$ 为有效胜场序列。现给定整数 $n$ 和 $m$，请计算满足 $W_1=m$ 且包含 $n$ 个整数的有效胜场序列数量。

思路

赛时在这里打表找规律耗费大量虚空时间，虽然过了。

其实就是一个很简单的二进制枚举，对于 $n(n-1)$ 场比赛二进制枚举胜者即可，然后判断胜利次数数组是否单调递减，$w_1$ 是否为 $m$，最后哈希判重。$O(2^{20}n)$，map 带常数。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned ll
const ll N=8,base=19260817;
ll n,m,s;
map<ull,bool>mp;
ll ans;
struct node
{ll x,y;
};
vector<node>G;
ll a[N];
void dfs(ll id)
{if(id==s){ull ha=0;ll ma=0;for(int i=1;i<=n;i++){ma=max(ma,a[i]);if(a[i]<a[i+1])return;ha=ha*base+a[i];}if(ma==m&&!mp[ha]){mp[ha]=1;ans++;}return;}a[G[id].x]++;dfs(id+1);a[G[id].x]--;a[G[id].y]++;dfs(id+1);a[G[id].y]--;
}
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j){G.push_back((node){i,j});}}}s=G.size();a[n+1]=-1;dfs(0);printf("%lld",ans);return 0;
}

D.#1495 奶牛求幂 / 洛谷 P10494 USACO02FEB Power Hungry Cows

题意

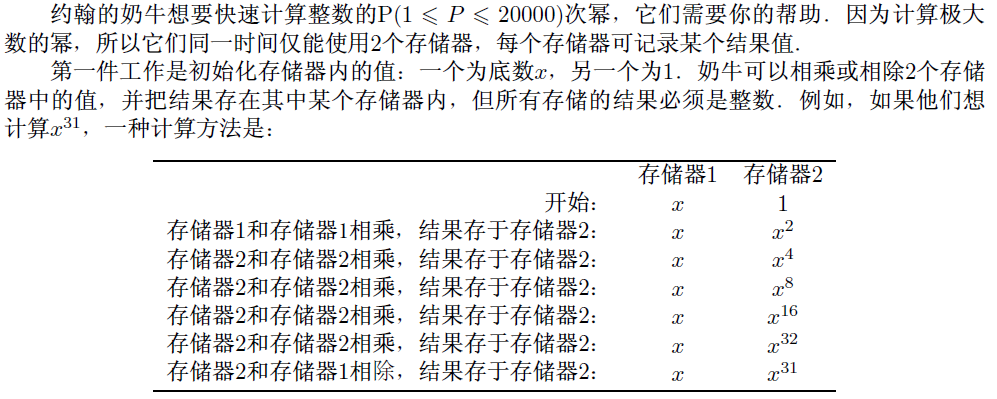
答案不超过 $18$。

思路

这题本来想用二进制去跳，但发现并非如此，因为可以左右相除。

把题目转化为两个数可以相加、相减、乘 $2$，期望得到 $n$ 的最小步数。那么可以直接 dfs 两个状态。

同时我们可以枚举期望答案从而限制 dfs 深度，因为题目说答案不超过 $18$，比较小。从而达到剪枝的目的。zc 说这叫 IDDFS。

bool dfs(ll x,ll y,ll stp)
{if(x<y)swap(x,y);//防止下面相除出问题if(stp>=ans){if(x==n||y==n)return 1;return 0;}if(dfs(x*2,x,stp+1)||//自己乘自己dfs(x*2,y,stp+1)||dfs(x,y*2,stp+1)||dfs(y,y*2,stp+1)||dfs(x+y,x,stp+1)||//两者相加dfs(x+y,y,stp+1)||dfs(x-y,x,stp+1)||//两者相减dfs(x-y,y,stp+1))return 1;return 0;
}

不过发现 50pts TLE，于是继续考虑剪枝。首先是如果两者中的最大值（此处强制 $x$ 更大）怎么 $\times 2$ 都不能达到 $n$，即 $x\times 2^{ans-stp}<n$，说明肯定无法得到 $n$，直接退出。

然后还是 TLE，因此考虑 $x,y$ 本身的性质：可能经过某些操作（如储存器自己乘自己，然后储存到另一个储存器），使得二者的 $d=\gcd (x,y)$ 较大且与 $n$ 互质；由于后面的操作（本质上都是加减）显然不会改变二者都是 $d$ 的倍数的特质，因此当 $d>1$ 且 $\gcd (d,n)=1$ 时也可以退出。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,ans;
bool dfs(ll x,ll y,ll stp)
{if(x<y)swap(x,y);if(stp>=ans){if(x==n||y==n)return 1;return 0;}if(n>(x<<(ans-stp)))return 0;//一直*2都不行 ll d=__gcd(x,y);if(d>1&&n%d)return 0;if(dfs(x*2,x,stp+1)||dfs(x*2,y,stp+1)||dfs(x,y*2,stp+1)||dfs(y,y*2,stp+1)||dfs(x+y,x,stp+1)||dfs(x+y,y,stp+1)||dfs(x-y,x,stp+1)||dfs(x-y,y,stp+1))return 1;return 0;
}
int main()
{scanf("%lld",&n);while(!dfs(1,0,0))ans++;printf("%lld",ans);return 0;
}

E.#15745 方格路径 K 大和 / AT_abc227_f Treasure Hunting

题意

有一个 $n$ 行 $m$ 列的网络，从上到下第 $i$ 行，从左到右第 $j$ 列的格子坐标为 $(i,j)$，其上写有整数 $a_{i,j}$。张三每次可以向右或者向下移动，不能超过边界，直到到达 $(n,m)$。

定义移动的代价为，经过的 $n+m-1$ 个格子中，前 $k$ 大数的和。求最小代价。

$1\le n,m\le 30$，$1\le k\le n+m$，$a_{i,j}\in [1,10^9]$。

思路

每次都是在这些题目上卡壳，尚需突破呢……zc 说这是全场质量最高的一题。

发现这题 $n,m$ 小的很，支持 $O(n^5)$。

发现不能把最大值和最小值加入 dp 状态，因为哪怕离散化之后值域也是 $O(n^2)$，而且不能用路径数个数据结构来维护一种合法路径的前 $k$ 大值。因此放弃在状态里表示和实时记录前 $k$ 大值。

可以考虑 $O(n^5)$ 怎么分配：枚举当前格子用 $O(n^2)$ 无可避免。我们发现前 $k$ 大这个限制依然很难搞，那么干脆分割一下：我们枚举期望的第 $k$ 大为 $a_{ki,kj}$，设 $f_{i,j,kk}$ 表示走到 $(i,j)$，前 $k$ 大已经填充了 $kk$ 个，的最小代价。

这样子，我们就可以判断，走到一个 $a_{i,j}$ 时，如果 $a_{i,j}>a_{ki,kj}$，那么它一定强制被算进前 $k$ 大，我们枚举 $kk$ 表示第 $k$ 大被填充到了第几个：
$$f_{i,j,kk}=\min (f_{i-1,j,kk-1},f_{i,j-1,kk}+a_{i,j})$$

如果 $a_{i,j}<a_{ki,kj}$，那么强制不把它加进前 $k$ 大。
$$f_{i,j,kk}=\min (f_{i-1,j,kk},f_{i,j-1,kk})$$

（注意可以从填充 $0$ 个也能转移过来，所以 $kk$ 可以为 $0$）

有个特殊情况就是 $a_{i,j}=a_{ki,kj}$，这种情况是既可以选也可以不选。因为假若加进去了，可能存在很多个 $a_{ki,kj}$ 相同值的数，于是这会可能成为第 $k+1$ 大数；但是有可能后面第 $k$ 大、$k-1$ 大、……都是值为 $a_{ki,kj}$ 的，因此还是有必要判断要不要加进去的。

这样子转移是正确的，因为每次都可以从 $0$ 个填充、$1$ 个填充、……$k-1$ 个填充转移过去，而 $f_{i-1,j,0\sim k}$ 与 $f_{i,j-1,0\sim k}$ 已经被更新为了目前最优状态。

而就算有一条路径上，比 $a_{ki,kj}$ 大的数多于 $k$ 个，因为强制加了这些比 $a_{ki,kj}$ 大的，这也不会是最优的；而枚举其它 $a_{k{i}^{\prime },k{j}^{\prime }}$ 恰好为第 $k$ 大时，这样的路径是会被计算到的。一句话就是，这样枚举每个数作为第 $k$ 大，都能保证每条可能路径都被统计到最优的 $k$ 大、$k-1$ 大、……

时间复杂度 $O(n^5)$。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=35,inf=0x3f3f3f3f;
ll n,m,k;
ll a[N][N];
ll f[N][N][N<<1];
//f(i,j,kk):钦定第k大为(ki,kj)，枚举到(i,j)，在前k大中有kk个数 
int main()
{scanf("%lld%lld%lld",&n,&m,&k);for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%lld",&a[i][j]);ll ans=8e14;for(int ki=1;ki<=n;ki++){for(int kj=1;kj<=m;kj++){memset(f,inf,sizeof(f));f[0][1][0]=f[1][0][0]=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]>a[ki][kj]){for(int kk=1;kk<=k;kk++){f[i][j][kk]=min(f[i][j][kk],f[i][j-1][kk-1]+a[i][j]);f[i][j][kk]=min(f[i][j][kk],f[i-1][j][kk-1]+a[i][j]);}}if(a[i][j]<a[ki][kj]){for(int kk=0;kk<=k;kk++){f[i][j][kk]=min(f[i][j][kk],f[i][j-1][kk]);f[i][j][kk]=min(f[i][j][kk],f[i-1][j][kk]);}}if(a[i][j]==a[ki][kj]){f[i][j][0]=min(f[i][j][0],min(f[i-1][j][0],f[i][j-1][0]));for(int kk=1;kk<=k;kk++){f[i][j][kk]=min(f[i][j][kk],f[i][j-1][kk-1]+a[i][j]);f[i][j][kk]=min(f[i][j][kk],f[i-1][j][kk-1]+a[i][j]);f[i][j][kk]=min(f[i][j][kk],f[i][j-1][kk]);f[i][j][kk]=min(f[i][j][kk],f[i-1][j][kk]);}}}}ans=min(ans,f[n][m][k]);}}printf("%lld",ans);return 0;
}

F.#21317 树上字符串匹配 / CF291E Tree-String Problem

题意

赛时给了个机翻的混淆题意，在临近最后改成了一个不说人话的题意，还是要看样例理解题意啊。

给一棵 $n$ 个节点的树，边的“权值”是字符串。边权的字符串可以拼接成一个字符串。

给一个模式串 $t$，问 $t$ 在树上出现了几次，匹配模式串可以跨过节点。

$n\le 10^5$，字符总数 $\le 5\times 10^5$。

样例输入

7
1 ab
5 bacaba
1 abacaba
2 aca
5 ba
2 ba
aba

样例输出

6

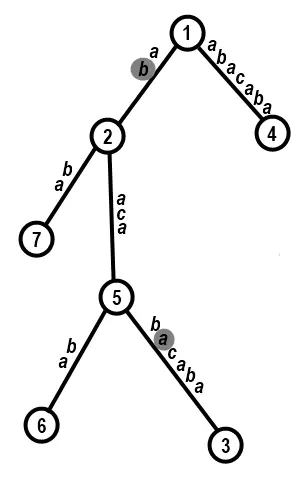
思路

dfs 遍历整棵树时，将字符一个一个加入当前串，然后匹配 $t$。注意匹配位置的结尾必须在当前枚举的边，否则就会重复算前继边的匹配。

实现可以用 substr 不过那玩意带 $O(|len|)$ 的常数啊，而且会爆空间。

代码1

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned ll
const ll N=5e5+2,base=131;
ll n;
string t;
ull Hash_t,pw[N];
void init()
{pw[0]=1;for(int i=1;i<N;i++)pw[i]=pw[i-1]*base;
}
struct edge
{ll to,next;string w;
}e[N<<1];
ll idx,head[N];
void addedge(ll u,ll v,string w)
{idx++;e[idx].to=v;e[idx].next=head[u];e[idx].w=w;head[u]=idx;
}
ll ans=0;
void dfs(ll u,ll fa,string cur,ll len)
{for(int i=head[u];i;i=e[i].next){ll v=e[i].to,tl=len;string w=e[i].w;if(v==fa)continue;string tem=cur,now=cur;if(len>=t.size())now=cur.substr(cur.size()-t.size(),t.size());//	cout<<u<<"->"<<v<<endl;for(int j=0;j<w.size();j++){tem+=w[j];if(now.size()>=t.size())now.erase(0,1);now+=w[j];//	cout<<":"<<tem<<": :"<<now<<":\n";tl++;if(tl>=t.size()){//	cout<<":"<<now<<": ";ans+=(now==t);}}//	cout<<":"<<tem<<":";dfs(v,u,tem,tl);}
}
int main()
{scanf("%lld",&n);for(int i=2;i<=n;i++){ll fa;string s;scanf("%lld",&fa);cin>>s;addedge(fa,i,s);addedge(i,fa,s);}cin>>t;for(int i=0;i<t.size();i++)Hash_t=Hash_t*base+(t[i]-'a'+1);dfs(1,0,"",0);printf("%lld",ans);return 0;
}

所以考虑使用哈希，在线找长度与模式串相同的子串，然后匹配。

代码2

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned ll
const ll N=5e5+2,base=131;
ll n;
string t;
ull Hash_t,pw[N];
void init()
{pw[0]=1;for(int i=1;i<N;i++)pw[i]=pw[i-1]*base;
}
struct edge
{ll to,next;string w;
}e[N<<1];
ll idx,head[N];
void addedge(ll u,ll v,string w)
{idx++;e[idx].to=v;e[idx].next=head[u];e[idx].w=w;head[u]=idx;
}
ll ans=0;
void dfs(ll u,ll fa,string cur,ll len)
{for(int i=head[u];i;i=e[i].next){ll v=e[i].to,tl=len;string w=e[i].w;if(v==fa)continue;string tem=cur,now=cur;if(len>=t.size())now=cur.substr(cur.size()-t.size(),t.size());//	cout<<u<<"->"<<v<<endl;for(int j=0;j<w.size();j++){tem+=w[j];if(now.size()>=t.size())now.erase(0,1);now+=w[j];//	cout<<":"<<tem<<": :"<<now<<":\n";tl++;if(tl>=t.size()){//	cout<<":"<<now<<": ";ans+=(now==t);}}//	cout<<":"<<tem<<":";dfs(v,u,tem,tl);}
}
int main()
{scanf("%lld",&n);for(int i=2;i<=n;i++){ll fa;string s;scanf("%lld",&fa);cin>>s;addedge(fa,i,s);addedge(i,fa,s);}cin>>t;for(int i=0;i<t.size();i++)Hash_t=Hash_t*base+(t[i]-'a'+1);dfs(1,0,"",0);printf("%lld",ans);return 0;
}