机器学习-Logistic Regression

一、逻辑回归

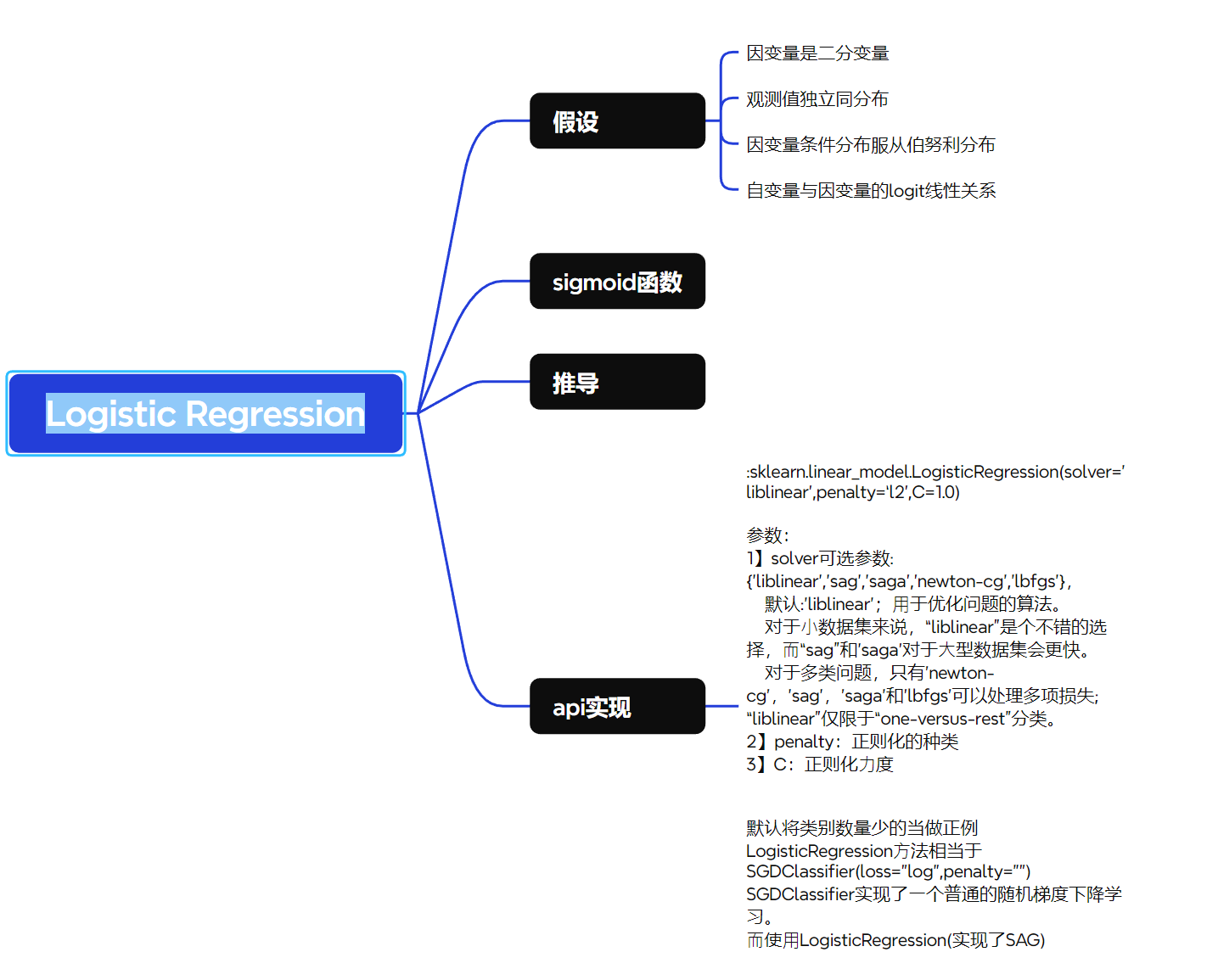
1 逻辑回归需要满足的假设

1 因变量是二分类变量：
逻辑回归模型假设响应变量为0或1的分类变量，适用于二分类问题。

2 观测值独立同分布（独立性）：
各样本之间相互独立，联合概率可分解为单个样本伯努利概率的乘积，从而构建极大似然函数。

3 因变量条件分布服从伯努利分布：
在给定自变量的条件下，因变量服从伯努利分布，其概率由逻辑函数（logistic function）确定。

4 自变量与因变量的logit线性关系：
自变量与因变量的对数几率（logit）存在线性关系，即$log(p/(1-p))=\beta 0+\beta 1x1+...+\beta kxk$。

5 线性判别函数假设：
逻辑回归假设存在一个线性函数
$$z=w^{T}x=w_0+w_1{x}_1+\cdots +w_k{x}_k$$
用于刻画输入特征对分类的“判别分数”，该线性组合是对数几率的线性部分，是模型的核心结构。

2 Sigmoid 函数

(sigmoid用于二分类，还有用于多分类的softmax)

2.1 定义

$g$ 代表一个常用的逻辑函数（logistic function）为$S$形函数（Sigmoid function），公式为： $g\left(z\right)=\frac{1}{1+e^{-z}}$
合起来，我们得到逻辑回归模型的假设函数：
$h\left(x\right)=\frac{1}{1+e^{-w^{T}x}}$

2.2 sigmoid的决策边界

默认是0.5，即大于0.5为正类，小于0.5为负类,如果需要调整，可以在逻辑回归输出的设定，比如改为大于0.7才为正类，sigmoid本身是不能变化的

3 逻辑回归的推导思路(目标函数最终为交叉熵)

1. 假设标签 y∈{0,1}y \in \{0, 1\}y∈{0,1}，且给定 $x$ 和参数 $w$ 后，$y$ 服从伯努利分布：
   (y是离散的，y的概率来自于伯努利分布)
   $$P(y|x;w)=\hat{p}(x;w{)}^y(1-\hat{p}(x;w){)}^{1-y}$$

2. 假设 $\hat{p}(x;w)$ 来自 sigmoid 函数：
   (给定自变量 $x$ 与参数 $w$ 的条件下，因变量的概率)
   $$\hat{p}(x;w)=\frac{1}{1+e^{-w^{T}x}}$$

3. 单个样本的条件概率密度(类似于边缘概率密度)：
   $$L(w)={\left(\frac{1}{1+e^{-w^T{x}^{(i)}}}\right)}^{y^{(i)}}{\left(1-\frac{1}{1+e^{-w^T{x}^{(i)}}}\right)}^{1-y^{(i)}}$$

4. 写出似然函数（所有样本概率连乘）(类似于联合概率密度)：
   $$L(w)=\prod _{i=1}^m{\left(\frac{1}{1+e^{-w^T{x}^{(i)}}}\right)}^{y^{(i)}}{\left(1-\frac{1}{1+e^{-w^T{x}^{(i)}}}\right)}^{1-y^{(i)}}$$

5. 取对数得到对数似然：
   $$\ell (w)=\sum _{i=1}^m\left[y^{(i)}\log \frac{1}{1+e^{-w^T{x}^{(i)}}}+(1-y^{(i)})\log \left(1-\frac{1}{1+e^{-w^T{x}^{(i)}}}\right)\right]$$

6. 最大化对数似然 ⇔ 最小化负对数似然（NLL）⇔交叉熵损失：
   $$J(w)=-\ell (w)=\sum _{i=1}^m\left[-y^{(i)}\log \frac{1}{1+e^{-w^T{x}^{(i)}}}-(1-y^{(i)})\log \left(1-\frac{1}{1+e^{-w^T{x}^{(i)}}}\right)\right]$$

7. 最后求偏导，进行梯度下降，寻找可以最小化负对数似然函数的参数 $w$
   
   
   $$J(w)=-\frac{1}{m}\sum _{i=1}^m(y_i-h_w(x_i))x_i^j$$

($h_w(x_i)$就是$\hat{p}(x;w)$,表示样本的概率)

8. 参数更新
   $$w_j=w_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_w(x_i)-y_i)x_i^j$$

4 注意点：

1、从上面的损失函数(负对数似然函数)可以发现，当y=1但$\widehat{p_i}$极小接近于0时，$log(\widehat{p_i})$会趋向于负无穷大，当y=0但$\widehat{p_i}$极大接近于1时，$log(\widehat{p_i})$也会趋向于负无穷大，这两种情况均会导致损失函数急剧增大。这说明逻辑回归对于异常值是非常敏感的)

2、当数据完全可分时，存在一个超平面可以完美地将两个类别分开，这意味着模型可以通过不断调整参数，使得似然函数趋向于无穷大（或负对数似然损失趋向于负无穷大）。这会导致系数趋于无穷,导致发散。这个问题可以通过正则化限制系数解决

3、之所以要用负对数似然是因为对数似然是凹函数，而负对数似然是凸函数(直观上其实是凹的，碗形，且只有一个“碗底”,非凸函数可能上上下下有很多)，便于优化,不易像对数似然那样陷入局部最优

4、最后的求导的函数里有1/m是因为这是对数似然的平均版本，即平均对数似然（average log-likelihood），表示每个样本的平均贡献，损失函数中，为了方便梯度大小和模型训练稳定，通常采用的是负平均对数似然（Negative Average Log-Likelihood）

5、普通逻辑回归不适用于时间序列，同线性回归，因为不满足残差独立同分布

6、逻辑回归的决策边界可以是非线性的

5 api

:sklearn.linear_model.LogisticRegression(solver=‘liblinear’,penalty=‘l2’,C=1.0)

参数：
1】solver可选参数:{‘liblinear’,‘sag’,‘saga’,‘newton-cg’,‘lbfgs’}，
默认:‘liblinear’；⽤于优化问题的算法。
对于⼩数据集来说，“liblinear”是个不错的选择，⽽“sag”和’saga’对于⼤型数据集会更快。
对于多类问题，只有’newton-cg’，‘sag’，'saga’和’lbfgs’可以处理多项损失;“liblinear”仅限于“one-versus-rest”分类。
2】penalty：正则化的种类
3】C：正则化⼒度

默认将类别数量少的当做正例
LogisticRegression⽅法相当于SGDClassifier(loss=“log”,penalty=“”)
SGDClassifier实现了⼀个普通的随机梯度下降学习。
⽽使⽤LogisticRegression(实现了SAG)

代码示例：

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression,Lasso,Ridge,GammaRegressor,LogisticRegression
from sklearn.preprocessing import MinMaxScaler,StandardScaler
from sklearn.metrics import mean_squared_error, r2_score,root_mean_squared_error,classification_report,confusion_matrix,roc_curve
from sklearn.model_selection import train_test_split, GridSearchCV, KFold
import joblib
from scipy import stats#%%
data = pd.read_csv('../data/diabetes.csv')
data
#%%
# 无缺失
data.isna().sum()
#%%
X = data.drop(columns="Outcome")
y= data["Outcome"]#%%
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2)#%%
# 标准化
transfer = StandardScaler()
transfer.fit(X_train)
X_train = transfer.transform(X_train)
X_test = transfer.transform(X_test)#%%
# 训练
estimater = LogisticRegression()
estimater.fit(X_train,y_train)
y_pred = estimater.predict(X_test)#%%
# 评估
report = classification_report(y_test,y_pred)
report
#%%
# ROC 
y_score = estimater.predict_proba(X_test)
fpr,tpr,_ = roc_curve(y_test,y_score[:,1])
plt.plot(fpr,tpr,label='ROC')
plt.plot([0,1],[0,1],linestyle='--')
plt.show()

6正则化逻辑回归*

regularized cost（正则化代价函数）

$$J\left(w\right)=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(h\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h\left(x^{(i)}\right)\right)]+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$

请注意等式中的"reg" 项。还注意到另外的一个“学习率”参数。这是一种超参数，用来控制正则化项。现在我们需要添加正则化梯度函数：
如果我们要使用梯度下降法令这个代价函数最小化，因为我们未对$w_0$ 进行正则化，所以梯度下降算法将分两种情形：

重复 直到 收敛  ⁣ ⁣{ ⁣ ⁣  w0:=w0−a1m∑i=1m[h(x(i))−y(i)]x0(i) wj:=wj−a1m∑i=1m[h(x(i))−y(i)]xj(i)+λmwj  ⁣ ⁣} ⁣ ⁣ 重复 \begin{align}& 重复\text{ }直到\text{ }收敛\text{ }\!\!\{\!\!\text{ } \\ & \text{ }{{w }_{0}}:={{w }_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{[{{h}}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}]x_{_{0}}^{(i)}} \\ & \text{ }{{w }_{j}}:={{w }_{j}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{[{{h}}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}]x_{j}^{(i)}}+\frac{\lambda }{m}{{w }_{j}} \\ & \text{ }\!\!\}\!\!\text{ } \\ & 重复 \\ \end{align} ​重复 直到 收敛 {  w0​:=w0​−am1​i=1∑m​[h(x(i))−y(i)]x0​(i)​ wj​:=wj​−am1​i=1∑m​[h(x(i))−y(i)]xj(i)​+mλ​wj​ } 重复​​
对上面的算法中 j=1,2,…,n 时的更新式子进行调整可得：
$w_j:=w_j(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum _{i=1}^m(h_w\left(x^{(i)}\right)-y^{(i)})x_j^{(i)}$

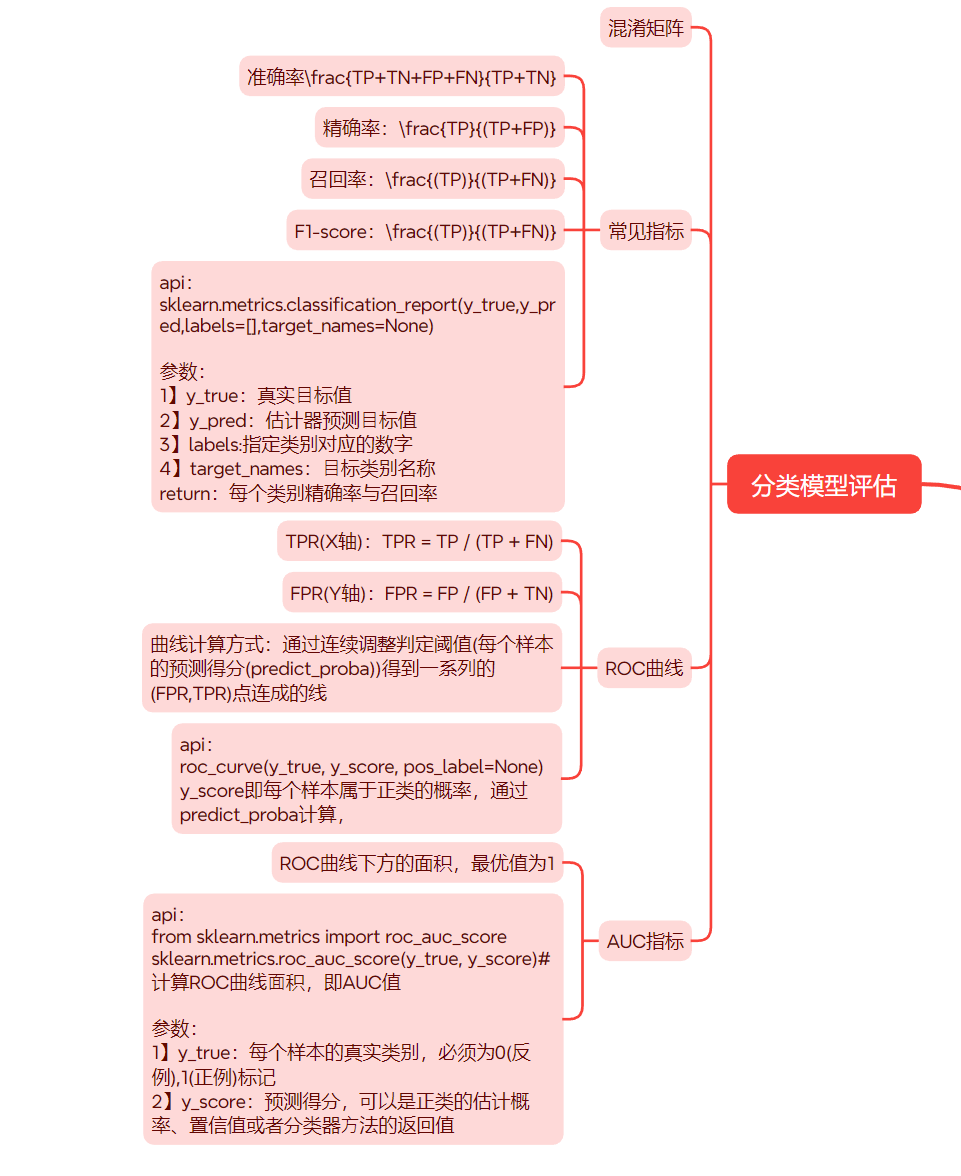
二、分类变量的评估

1 混淆矩阵

(T为True，F为False，P为Positive，N为Negative)

1.1 混淆矩阵

在分类任务下，预测结果与正确标记之间存在四种不同的组合，构成混淆矩阵(适⽤于多分类)

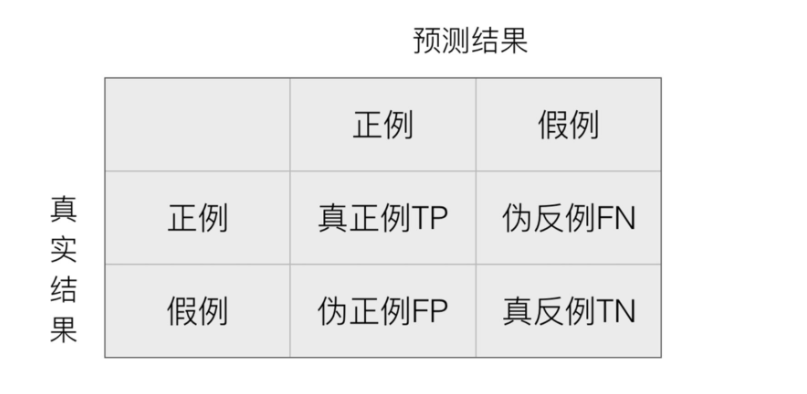
1.2 api

confusion_matrix

2常见指标

2.1 准确率

准确率： $\frac{TP+TN+FP+FN}{TP+TN}$

2.2 精确率与召回率

精确率：预测结果为正例样本中真实为正例的⽐例
精确率：$\frac{TP}{(TP+FP)} $

召回率：真实为正例的样本中预测结果为正例的⽐例（查得全，对正样本的区分能⼒）
召回率：$\frac{(TP)}{(TP+FN)} $

2.3 F1-score

F1-score作用：衡量模型的稳健型
F1-score：$\frac{2TP}{2TP+FN+FP}$

2.4 混淆矩阵api

sklearn.metrics.classification_report(y_true,y_pred,labels=[],target_names=None)

参数：
1】y_true：真实⽬标值
2】y_pred：估计器预测⽬标值
3】labels:指定类别对应的数字
4】target_names：⽬标类别名称
return：每个类别精确率与召回率

3 ROC曲线

3.1 TPR与FPR

TPR = TP / (TP + FN) 【TPR == 召回率】
# 所有真实类别为1的样本中，预测类别为1的⽐例
FPR = FP / (FP + TN)
# 所有真实类别为0的样本中，预测类别为1的⽐例

TPR 就是预测正确的情况 FDR就是预测错误的情况，TPR和FDR形成了ROC的曲线

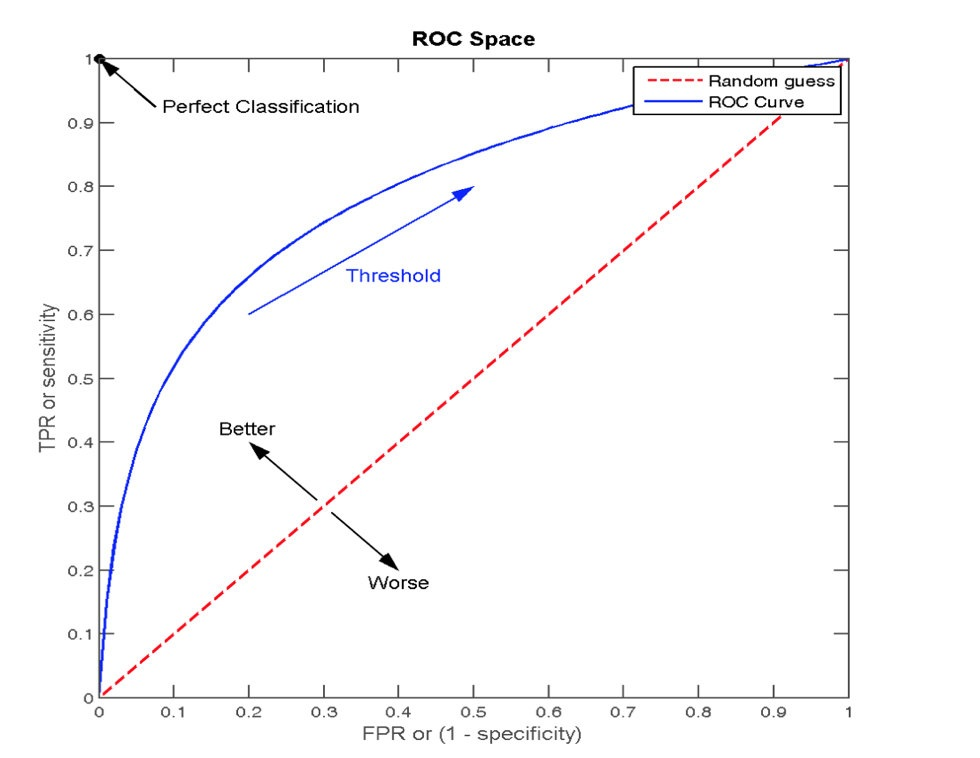
3.2 ROC曲线

ROC曲线的横轴就是FPRate，纵轴就是TPRate
当⼆者相等时，表示的意义则是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的，此时AUC为0.5

ROC曲线是什么？‌

• X轴‌：FPR（误杀率）
• Y轴‌：TPR（抓捕率）
• ‌曲线怎么来的‌：通过连续调整判定阈值(每个样本的预测得分)得到一系列的(FPR,TPR)点连成的线
  
  
  

3.3 ROC api

roc_curve(y_true, y_score, pos_label=None)
y_score即每个样本属于正类的概率，通过predict_proba计算，

4 AUC

4.1 AUC指标

AUC是什么？‌

• 就是ROC曲线下方的面积（Area Under Curve）
• ‌物理意义‌：随机选一个垃圾邮件和一个正常邮件，你的模型给垃圾邮件打分更高的概率
• ‌范围‌：0.5（瞎猜）~1（完美）

4.2 AUC计算api

from sklearn.metrics import roc_auc_score
sklearn.metrics.roc_auc_score(y_true, y_score)# 计算ROC曲线⾯积，即AUC值

参数：
1】y_true：每个样本的真实类别，必须为0(反例),1(正例)标记
2】y_score：预测得分，可以是正类的估计概率、置信值或者分类器⽅法的返回值

ROC绘制示例：

from matplotlib import pyplot as plt
from sklearn.metrics import roc_curvey_true = [0, 1, 0, 1, 0, 1]       # 真实标签（0=负类，1=正类）
y_score = [0.2, 0.7, 0.3, 0.6, 0.1, 0.8]  # 模型预测得分
fpr, tpr, _ = roc_curve(y_true, y_score)
plt.plot(fpr,tpr,color="blue",label="ROC")
plt.plot([0,1],[0,1],color="red",linestyle="--")
#
plt.title("ROC")
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.legend()
plt.grid()
plt.show()
#%%
y_true = [1, 0, 0, 1, 1, 0, 1, 0]
y_score = [0.8, 0.5, 0.5, 0.7, 0.6, 0.5, 0.9, 0.3]fpr, tpr, _ = roc_curve(y_true, y_score)
plt.plot(fpr,tpr,color="blue",label="ROC")
plt.plot([0,1],[0,1],color="red",linestyle="--")
#
plt.title("ROC")
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.legend()
plt.grid()
plt.show()
#%%
y_true = [0, 0, 0, 0, 0, 0, 1, 0, 1, 0]  # 2个欺诈（正类），8个正常（负类）
y_score = [0.1, 0.2, 0.15, 0.05, 0.3, 0.25, 0.9, 0.4, 0.6, 0.1]  # 模型输出的欺诈
fpr, tpr, _ = roc_curve(y_true, y_score)
plt.plot(fpr,tpr,color="blue",label="ROC")
plt.plot([0,1],[0,1],color="red",linestyle="--")
#
plt.title("ROC")
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.legend()
plt.grid()
plt.show()