【Open3D】基础操作之三维数据结构的高效组织和管理

【Open3D】基础操作之三维数据结构的高效组织和管理

---

前言

点云数据结构是一种以离散三维点集为核心，辅以丰富属性信息，用于精确描述三维物体表面或场景空间形态的数据表示方法。本质上是一组离散的、无序的点的集合，其无序、稀疏、非均匀、无拓扑的特性带来了独特的处理挑战。
八叉树（Octree）和 KD 树（K-Dimensional Tree）是两种空间划分数据结构，专门用于高效组织和管理三维点云数据，以解决点云无序性、稀疏性、大规模性带来的处理瓶颈（如最近邻搜索、范围查询、降采样等）。它们通过将空间递归细分，建立层次结构，显著加速空间查询操作。

---

Octree（八叉树）

原理介绍

核心思想： 递归地将三维空间均等分割成 8 个立方体子空间（八分体），直到每个子空间满足特定条件，如包含的点数少于阈值、达到最大深度等。

递归的空间均分

• 起始：将整个三维空间（初始立方体）定义为八叉树的根节点。
  

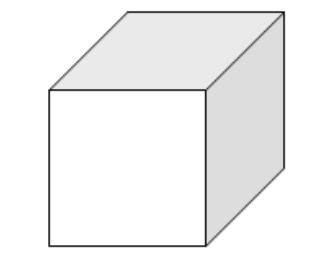
• 分割：如果当前节点（立方体）中包含的点数量超过了预设的最大阈值（max_points_per_node）并且当前节点的深度小于预设的最大深度（max_depth），则执行以下操作：

  • 沿着 X, Y, Z 三个坐标轴的中点，将这个立方体均等分割成 8 个更小的、体积相等的子立方体（称为八分体或体素）。
  • 为这 8 个子立方体创建对应的 8 个子节点，作为当前节点的孩子。
    

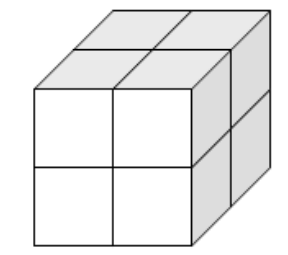
  规则划分： 每一次分割都是等分的、轴对齐的。所有子节点代表的立方体大小相同，是父节点体积的 1/8。空间划分完全独立于点云的具体分布，只依赖于初始边界框和分割深度。

• 递归：对每一个新创建的子节点（子立方体），重复步骤 2。检查它内部点的数量和当前深度，决定是否需要进一步分割。

• 终止：递归分割在以下任一条件满足时停止：

  • 当前节点（立方体）包含的点数 <= 预设的最大阈值 max_points_per_node；
  • 当前节点的深度 == 预设的最大深度 max_depth；
  • 当前节点（立方体）内没有点（空节点）。
    

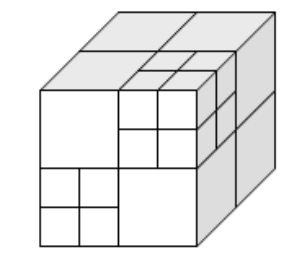
  体素 (Voxel)： 叶子节点所代表的最小立方体单元，是空间分割的最终结果。可以看作是三维空间中的“像素”。

存储

非叶子节点：只存储指向其 8 个子节点的指针（或索引），以及描述它所代表的空间范围的信息，通常是中心点和半边长。
叶子节点：存储落入它所代表的最终子立方体（体素）内的所有点，或者这些点的索引、指针，以及空间范围信息。

有些实现中，叶子节点也可能存储该体素内点的聚合信息（如中心点、平均颜色、点数量）。

下图即树形结构示意图：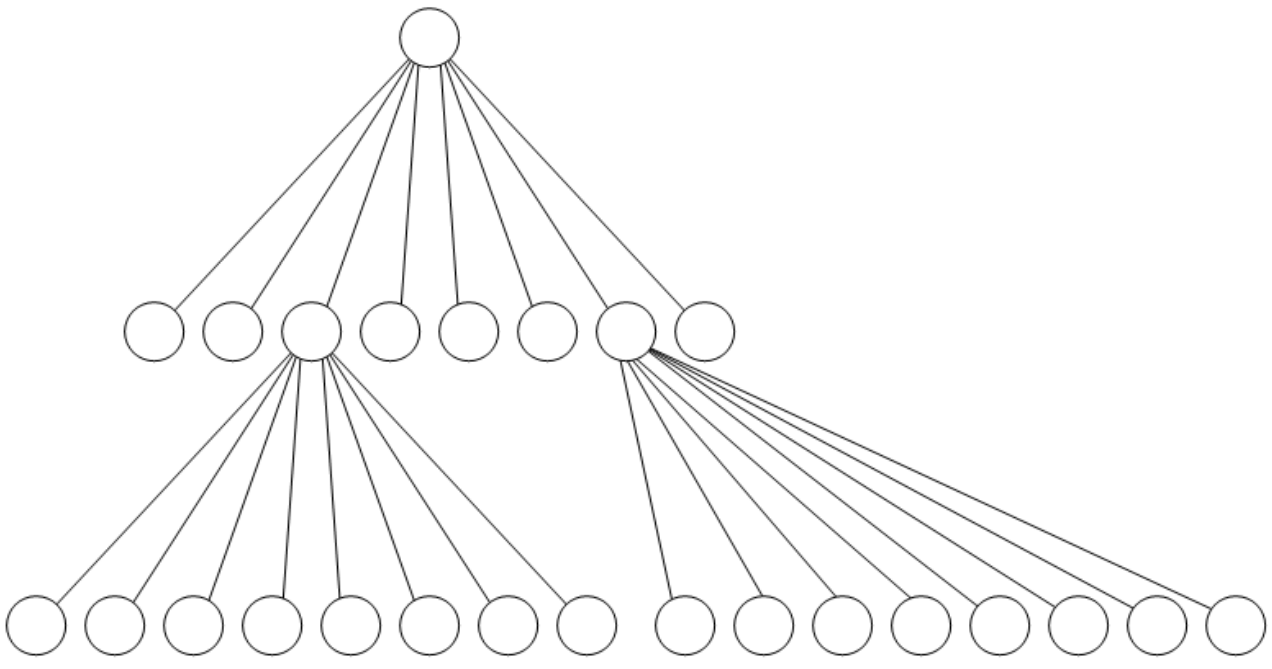

• 根节点 (Root)：代表整个点云空间
• 内部节点 (Internal Node)：拥有子节点的节点，它存储子节点指针和空间范围，不直接存储点；
• 叶子节点 (Leaf Node)：没有子节点的节点，它直接存储点（或索引）和空间范围；
• 深度 (Depth)：根节点深度为 0，每向下一层深度加 1。深度反映了空间分辨率，深度越大的节点代表的体素越小；
• 层/级 (Level)：与深度同义，也可能指从叶子节点往上数的层数（叶子为第 0 层）。

八叉树天然具有层次性，较浅的节点（上层）代表较大的空间区域和较低的分辨率（点被聚合）；较深的节点（下层）代表较小的空间区域和较高的分辨率（点更精细）。

点云搜索

• 点查询 (Point Query)，时间复杂度接近 $O(logN)$：
  • 给定一个点坐标 (x, y, z)。
  • 从根节点开始，根据点的坐标，确定它位于当前节点的哪个子节点（八分体）中，移动到对应的子节点，递归此过程，直到到达叶子节点。
  • 检查该点是否确实存在于该叶子节点存储的点集中（精确匹配）。
• 范围搜索 (Range Search / Box Query)，时间复杂度通常在 $O(logN+K)$ 到 $O(N)$ 之间，$K$ 是结果点数：
  • 给定一个查询区域，通常是一个轴对齐的包围盒 。
  • 从根节点开始，检查当前节点的空间范围与查询区域的相交关系。
  • 不相交则忽略该节点及其所有子树。
  • 完全包含则将该节点子树中所有叶子节点存储的点都加入到结果集中。
  • 部分相交，如果当前节点是叶子节点，检查其存储的每个点是否在查询区域内，将符合条件的点加入结果集；如果当前节点是内部节点，递归地对所有 8 个子节点执行范围搜索。
• K 最近邻搜索 (K-Nearest Neighbor Search - KNN)，
  • 先快速定位查询点所在的叶子节点，将该叶子节点内的点作为候选集，计算距离，找出当前 K 个最近邻。
  • 计算查询点到当前节点或叶子节点边界的最近距离 d_min，检查查询点到当前 K 个最近邻中最远点的距离 d_knn。
  • 回溯，从当前叶子节点向上回溯父节点，对于每个回溯到的父节点，检查其未被访问过的子节点。
  • 如果查询点到该子节点空间范围的最小可能距离 d_possible_min 小于当前最远点的距离 d_knn ，则说明该子节点代表的区域内可能存在比当前 K 个最近邻更近的点，需要递归搜索该子节点。
  • 在搜索过程中不断更新候选的 K 个最近邻和最远点的距离 d_knn。

  八叉树本身不是为高效 KNN 设计的，后续讲解的KD树更优，但可以实现。

o3d.geometry.Octree（八叉树数据结构的类）

用于高效管理三维空间数据，如点云、网格。

o3d.geometry.Octree（八叉树对象的构造函数）

函数原型

octree = o3d.geometry.Octree(max_depth)

参数	参数说明
max_depth (int)	八叉树的最大深度，深度从0开始，根节点深度为0。

返回值	返回值说明
octree (o3d.geometry.Octree)	返回一个空的八叉树对象。基于 max_depth 仅定义了空间划分的框架，但还没有包含任何实际的点云数据。

o3d.geometry.Octree.convert_from_point_cloud（将点云数据转换为八叉树结构的函数）

函数原型

Octree.convert_from_point_cloud(point_cloud, size_expand=0.01)

没有显式返回值，直接修改调用它的Octree对象。

参数	参数说明
point_cloud (o3d.geometry.PointCloud)	输入点云数据。
size_expand (float,默认0.01)	边界框扩展因子，用于确保所有点被包含。

计算点云边界框：基于点云中所有点的坐标计算最小包围盒，确保点云边缘的点能被包含。

扩展后尺寸 = 原始尺寸 × (1 + size_expand)

示例：

import open3d as o3d    # 导入Open3D库
pcd = o3d.io.read_point_cloud("tooth.ply")     # 读取点云数据
pcd.paint_uniform_color([1.0, 1.0, 0.0])    # 设置颜色
octree = o3d.geometry.Octree(max_depth=10)      # 初始化八叉树,设置最大深度
octree.convert_from_point_cloud(pcd, size_expand=0.1)       # 构建八叉树,确保点都被包含
o3d.visualization.draw_geometries([octree], window_name="八叉树",width=1600,height=1200)      # 可视化

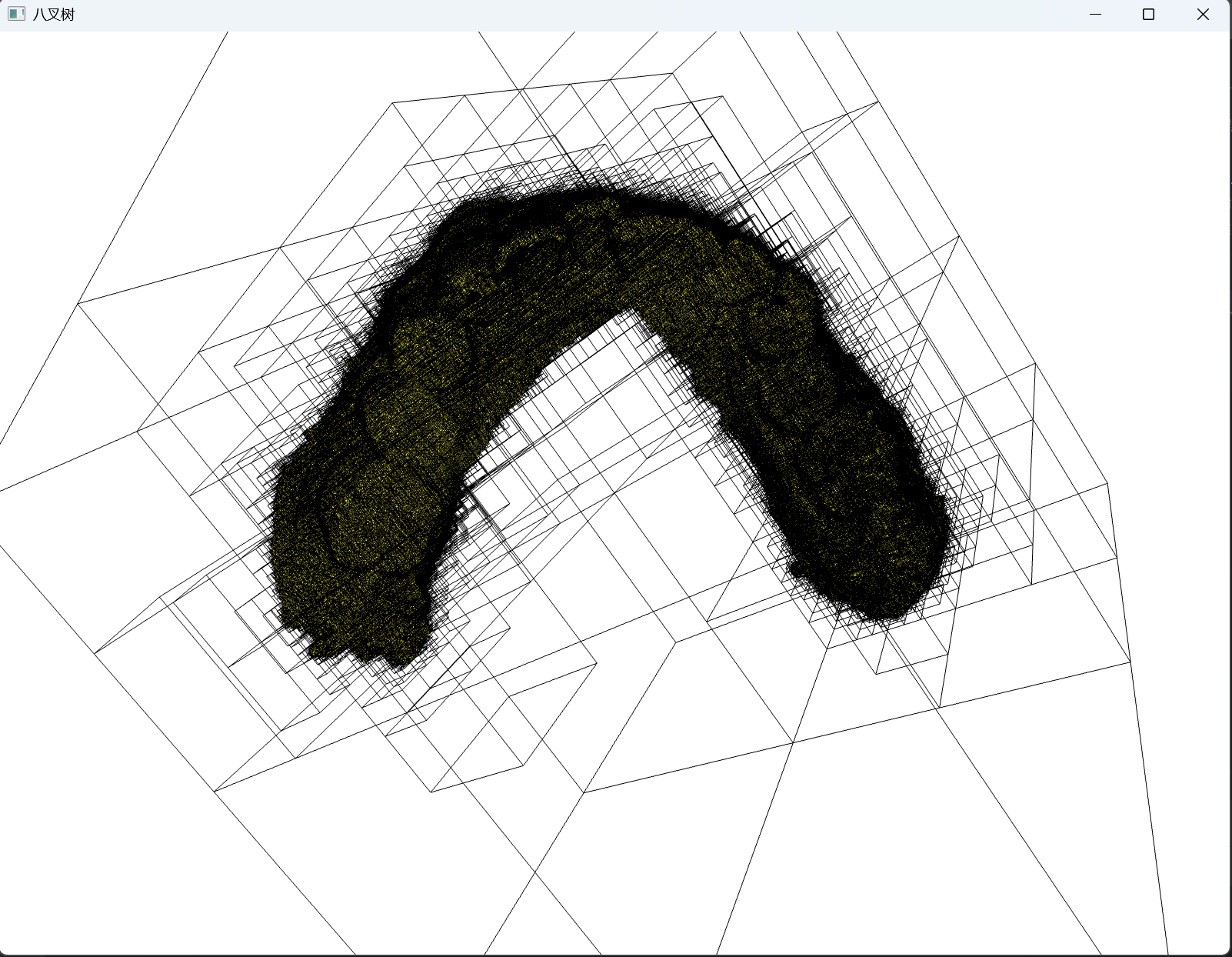
同样大小的立方体属于同一层次和分辨率，不同大小的立方体对应不同的层次和分辨率。

o3d.geometry.Octree.create_from_voxel_grid（将体素网格转换为八叉树结构）

函数原型

Octree.create_from_voxel_grid(voxel_grid)

没有显式返回值，直接修改调用它的Octree对象。

参数	参数说明
voxel_grid (o3d.geometry.VoxelGrid )	输入体素网格数据。

示例：

import open3d as o3d    # 导入Open3D库
pcd = o3d.io.read_point_cloud("tooth.ply")     # 读取点云数据
pcd.paint_uniform_color([1.0, 1.0, 0.0])    # 设置颜色
voxel_grid = o3d.geometry.VoxelGrid.create_from_point_cloud(pcd, voxel_size=0.05)	# 创建体素网格 (体素尺寸=0.05)
octree = o3d.geometry.Octree(max_depth=10)      # 初始化八叉树,设置最大深度
octree.create_from_voxel_grid(voxel_grid)       # 构建八叉树,确保点都被包含
o3d.visualization.draw_geometries([octree], window_name="八叉树",width=1600,height=1200)      # 可视化

---

K-Dimensional Tree（KD树 ）

原理介绍

核心思想： 递归地使用超平面（在 3D 中是平面）沿某一坐标轴将空间二分。每次分割选择当前点集在某个维度上的中位数作为分割点，确保左右子树尽可能平衡。

数据驱动的递归空间二分

• 选择分割维度 (Split Dimension)：在当前节点所代表的点集和空间范围内，选择一个坐标轴（维度）来进行分割。 常见策略：

  • 轮转选择 (Round Robin)：最常见的方式。在树的每一层，依次循环选择维度，例如：根节点用 X 轴，下一层用 Y 轴，再下一层用 Z 轴，然后回到 X 轴，如此往复。这种方式简单且通常能产生比较平衡的树。
  • 最大方差维度 (Max Variance)： 选择当前点集在该维度上坐标值方差最大的那个维度。方差大意味着数据在该维度上“铺得最开”，分割后能更有效地减少子空间的大小。这通常能构建出更优的树，但计算方差增加了构建成本。
    

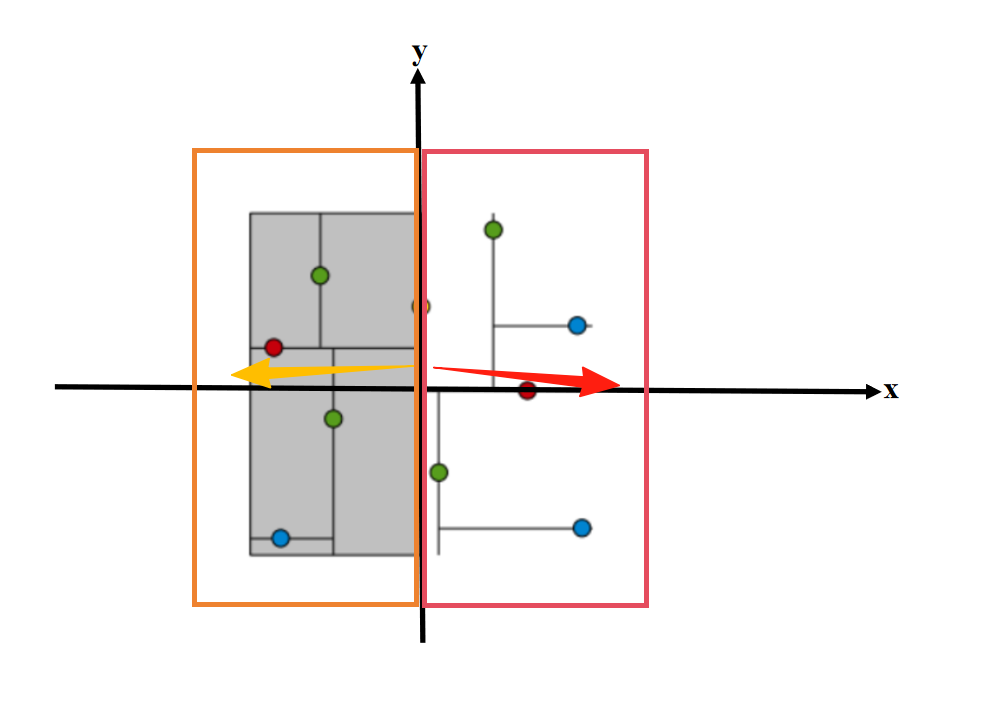
  选定 X 轴维度来进行分割，大致分成俩部分。

• 选择分割点 (Split Value)：在选定的分割维度上，选择一个值来定义分割超平面（在 3D 中是平面）。核心目标是使分割后左右子树的点数量尽可能相等，以保持树的平衡。常见策略：

  • 中位数法 (Median)：最常用且推荐的方法。 找到选定维度上所有坐标值的中位数。将小于中位数的点划分到左子树，大于或等于中位数的点划分到右子树。这保证了树的深度大约是 $O(logN)$，并且左右子树尽可能平衡。
  • 平均值法 (Mean)：使用选定维度上坐标值的平均值。计算简单，但不推荐，因为它不能保证树的平衡（受异常点影响大），可能导致退化成链表，破坏 $O(logN)$ 的优势。
    

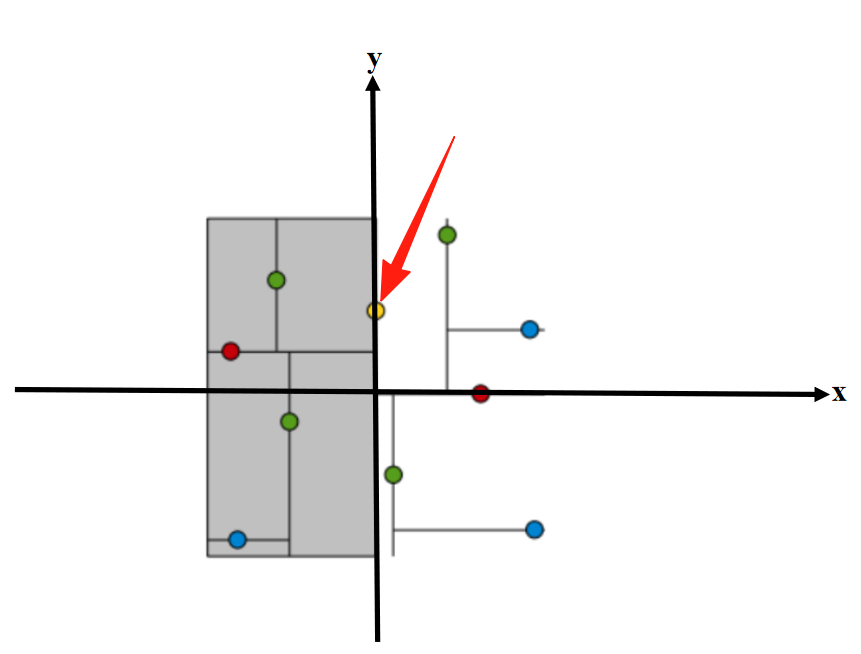
  维度选定后，需要确定具体分割点进行分割，来保持点数量尽可能相等。

• 递归构建： 对左子树和右子树代表的点集和子空间，递归地重复步骤 1 和 2，直到满足终止条件。递归在以下任一条件满足时停止：

  • 当前节点包含的点数 <= 预设的叶子节点容量 leaf_size 。
  • 当前节点所代表的空间范围内没有点。
  • 达到预设的最大树深度。
    

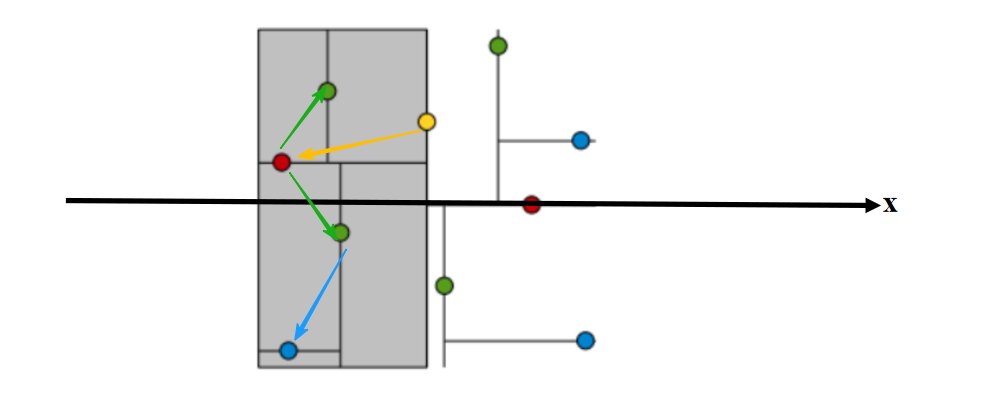
例如，上图中，总的空间划分成左空间和右空间，左空间又被划分成左上空间和左下空间，左下空间又被划分成左下右子空间和左下左子空间，以此类推。

存储

非叶子节点：存储分割维度, 分割点，以及指向左、右子节点的指针。
叶子节点：存储一个指向点列表（或索引数组）的指针和点的数量 。

整个 KD 树结构本身不存储点的坐标副本，它存储的是对原始点云数据的引用（索引/指针）和划分信息。除非叶子节点直接存点，原始点集通常存储在一个连续的数组中。

下图即树形结构示意图：

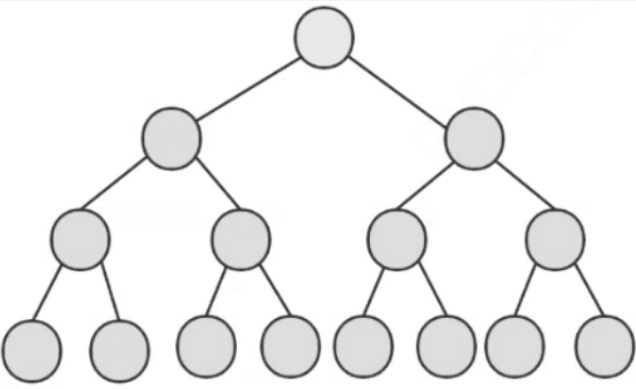
• 根节点 (Root)：代表整个点云空间。
• 内部节点 (Internal Node)：拥有子节点的节点，用于划分空间的超平面，它存储分割维度和一个分割值，以及包含指向其左子树 (left child) 和右子树 (right child) 的指针/引用，不存储数据点本身；
• 叶子节点 (Leaf Node)：没有子节点的节点，存储该节点包含的所有数据点或者这些点的索引/指针，以及这些点的数量；
• 深度 (Depth)：根节点深度为 0，每向下一层深度加 1。深度反映了空间分辨率，深度越大的节点代表的体素越小；
• 层/级 (Level)：与深度同义，也可能指从叶子节点往上数的层数（叶子为第 0 层）。

点云搜索

• 半径搜索 (Radius Search / Range Search)，时间复杂度通常在 $O(logN+K)$ ，$K$ 是结果点数：

  • 给定一个查询点Q和一个半径R。
  • 获得查询点Q在该节点的分割维度上的坐标Q[split_dim]，计算 Q 到分割超平面的距离d_split = |Q[split_dim] - split_value|。
  • 选择搜索左子树，如果 Q[split_dim] < split_value 且 d_split <= R，即查询点Q坐标落在左子树，且搜索半径没有越过超平面。
  • 选择搜索右子树，如果 Q[split_dim] >= split_value 且 d_split <= R，即查询点Q坐标落在右子树，且搜索半径没有越过超平面。
  • 两个子树都需要搜索，坐标落在某个子树，但是搜索半径越过超平面到另一个子树内。
  • 从根节点开始，递归搜索，如果当前节点是叶子节点，计算查询点Q到该叶子节点内所有点的距离，将所有距离<= R的点加入结果集。

• K 最近邻搜索 (K-Nearest Neighbor Search - KNN)

  • 从初始根节点开始，沿着树向下走到可能包含最近邻的叶子节点。
  • 遇到内部节点：获取查询点Q在该节点的分割维度上的坐标Q[split_dim]，根据节点的分割值split_value判断查询点Q的落点。Q[split_dim] < split_value，优先递归搜索左子树；否则优先递归搜索右子树。
  • 到达叶子节点，计算查询点Q到该叶子节点内所有点的距离。堆未满则直接插入点及其距离；若堆已满，将堆内距离最大的点作为堆顶点，比较新的点的距离与堆顶点的距离，距离大于堆顶点的距离则忽略，小于就将新的点替换堆顶的点，然后重新将堆内距离最大的点作为堆顶点。
  • 回溯到上层（内部）节点时，计算查询点Q到该节点分割超平面的最短距离 d_split = |Q[split_dim] - split_value|，并获取当前堆顶的距离 d_max。如果 d_split < d_max，说明在未搜索的子树中可能存在比当前第 K 近邻更近的点，此时需要搜索那个未探索的子树；如果 d_split >= d_max，未探索的子树中不可能有比当前堆顶更近的点。可以安全地跳过对该子树的搜索。
  • 如果决定搜索另一个子树，则对该子树执行向下遍历到叶子节点的过程；否则继续回溯到上一层节点。
  • 当回溯到根节点并完成所有必要子树的搜索后，堆中存储的点就是 查询点Q的 K 个最近邻点。

o3d.geometry.KDTreeFlann（高效最近邻搜索的核心类）

o3d.geometry.KDTreeFlann（KD树对象的构造函数）

函数原型

kdtree = o3d.geometry.KDTreeFlann(geometry)

参数	参数说明
geometry (open3d.geometry.PointCloud, open3d.geometry.VoxelGrid, open3d.utility.Vector3dVector)	用于构建 KD 树的几何数据。可以是点云、体素网格或三维向量数组。

返回值	返回值说明
kdtree (o3d.geometry.KDTreeFlann)	已构建好索引的 KDTreeFlann 对象实例。

o3d.geometry.KDTreeFlann.search_knn_vector_3d（K-近邻搜索函数）

函数原型

num_found, indices, sqr_distances = KDTreeFlann.search_knn_vector_3d(query, k)

参数	参数说明
query (List[float],numpy.ndarray)	查询点的三维坐标 [x, y, z]，可以是原始点云中的一个点，也可以是空间中的任意一点。
k (int)	要搜索的最近邻点的数量。

返回值	返回值说明
num_found (int)	实际找到的邻居数量。通常等于 k，除非点云中的总点数少于 k。
indices (List[int])	找到的最近邻点在原始几何体中的索引列表。这些索引可用于访问原始点云中的对应点、颜色、法向量等属性。
sqr_distances (List[float])	查询点到每个找到的最近邻点的平方欧几里得距离列表。注意：返回的是距离的平方，而不是原始距离。

示例：

import open3d as o3d    # 导入Open3D库
import numpy as np
pcd = o3d.io.read_point_cloud("tooth.ply")   # 读取点云数据
pcd.paint_uniform_color([1.0, 1.0, 0.0])    # 设置颜色
kdtree = o3d.geometry.KDTreeFlann(pcd)  # 构建KD树
query_point = pcd.points[0]  # 定义一个查询点 (这里以点云的第一个点为例),也指定任意的[x,y,z] 坐标
k = 10000  # 设置要搜索的最近邻点的数量
[num_found, indices, sqr_distances] = kdtree.search_knn_vector_3d(query_point, k)   # 执行 KNN 搜索
print(f"在点云中找到了 {num_found} 个最近邻点。")
print(f"这些点在原始点云中的索引为: {indices}")
print(f"到查询点的平方距离为: {sqr_distances}")
distances = np.sqrt(sqr_distances)  # 计算实际距离
print(f"到查询点的实际距离为: {distances}")
neighbor_points = np.asarray(pcd.points)[indices]   # 获取最近邻点的坐标
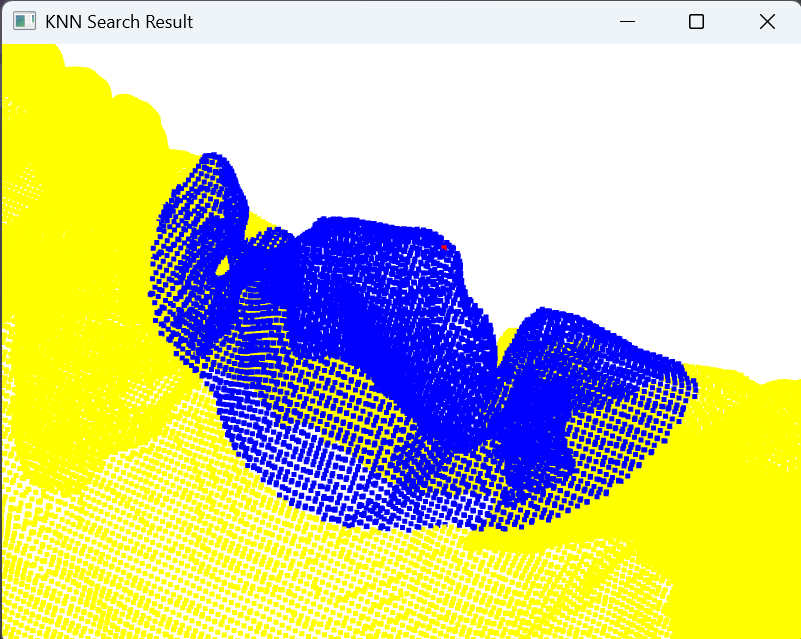
print(f"最近邻点的坐标为:\n{neighbor_points}")# -----可视化查询点和找到的邻居-----
query_pcd = o3d.geometry.PointCloud()   # 创建一个包含查询点的点云
query_pcd.points = o3d.utility.Vector3dVector([query_point])
query_pcd.paint_uniform_color([1, 0, 0])    # 红色表示查询点neighbors_pcd = o3d.geometry.PointCloud()   # 创建一个包含最近邻点的点云
neighbors_pcd.points = o3d.utility.Vector3dVector(neighbor_points)
neighbors_pcd.paint_uniform_color([0, 0, 1])  # 蓝色表示邻居点o3d.visualization.draw_geometries([query_pcd, neighbors_pcd,pcd],   window_name="KNN Search Result",width=800, height=600,point_show_normal=False)  # 可视化原始点云、查询点和邻居点
# -----可视化查询点和找到的邻居-----

o3d.geometry.KDTreeFlann.search_radius_vector_3d（半径搜索函数）

函数原型

num_found, indices, sqr_distances = KDTreeFlann.search_radius_vector_3d(query, radius)

参数	参数说明
query (List[float],numpy.ndarray)	查询点的三维坐标 [x, y, z]，可以是原始点云中的一个点，也可以是空间中的任意一点。
radius (float)	搜索的半径，所有距离小于或等于此半径的点都会被找到。

返回值	返回值说明
num_found (int)	实际在半径内找到的邻居数量。通常数量是动态的，取决于查询点周围的点密度和 radius 的大小。
indices (List[int])	找到的所有在半径内的邻居点的索引。这些索引可用于访问原始点云中的对应点、颜色、法向量等属性。
sqr_distances (List[float])	查询点到每个找到的对应邻居点的平方欧几里得距离列表。注意：返回的是距离的平方，而不是原始距离。

示例：

import open3d as o3d    # 导入Open3D库
import numpy as np
pcd = o3d.io.read_point_cloud("tooth.ply")   # 读取点云数据
pcd.paint_uniform_color([1.0, 1.0, 0.0])    # 设置颜色
kdtree = o3d.geometry.KDTreeFlann(pcd)  # 构建KD树
query_point = pcd.points[0]  # 定义一个查询点 (这里以点云的第一个点为例),也指定任意的[x,y,z] 坐标
radius = 5    # 设置要搜索的半径大小
[num_found, indices, sqr_distances] = kdtree.search_radius_vector_3d(query_point, radius)   # 执行半径搜索
print(f"在点云中找到了 {num_found} 个最近邻点。")
print(f"这些点在原始点云中的索引为: {indices}")
print(f"到查询点的平方距离为: {sqr_distances}")
distances = np.sqrt(sqr_distances)  # 计算实际距离
print(f"到查询点的实际距离为: {distances}")
neighbor_points = np.asarray(pcd.points)[indices]   # 获取最近邻点的坐标
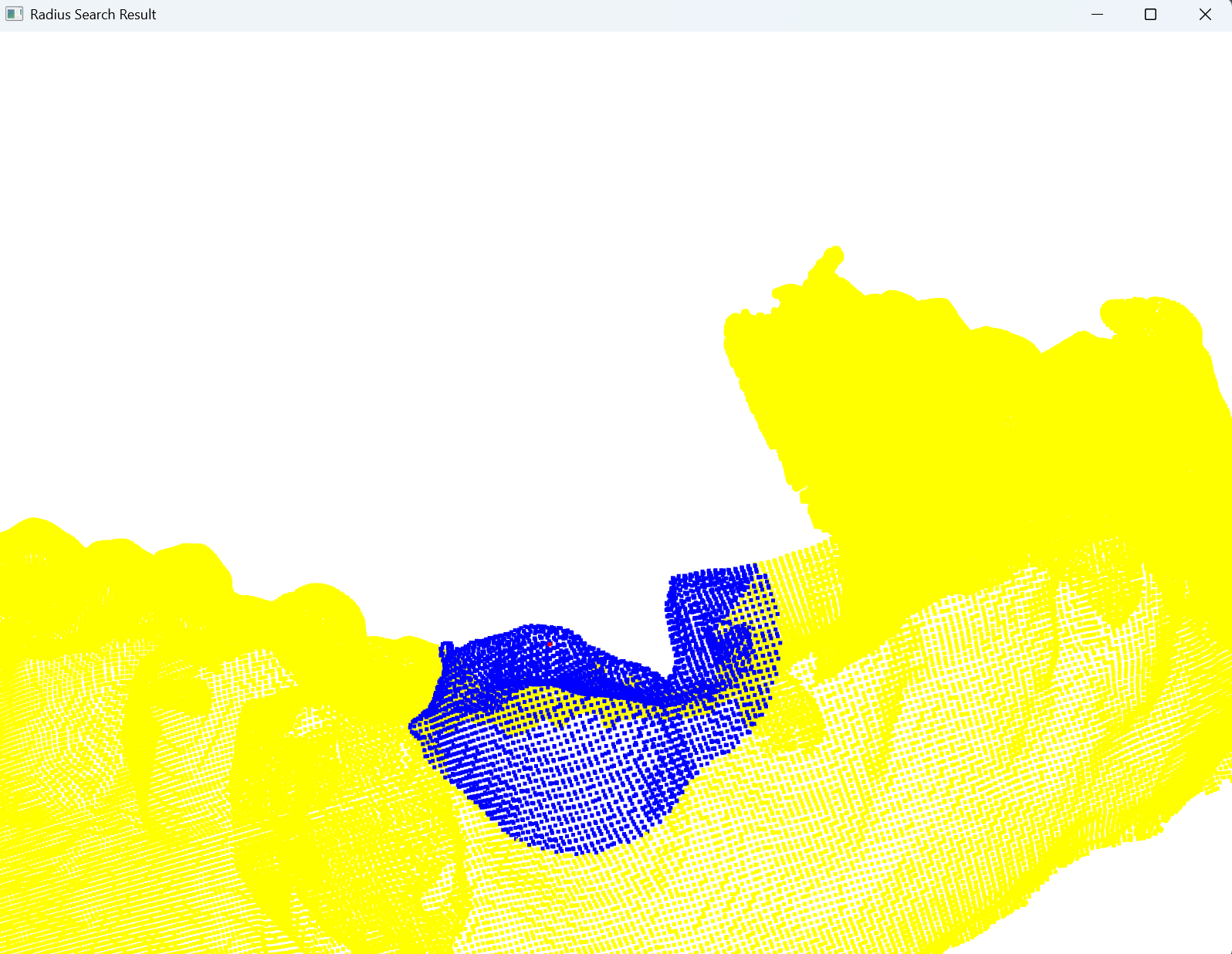
print(f"最近邻点的坐标为:\n{neighbor_points}")# -----可视化查询点和找到的邻居-----
query_pcd = o3d.geometry.PointCloud()   # 创建一个包含查询点的点云
query_pcd.points = o3d.utility.Vector3dVector([query_point])
query_pcd.paint_uniform_color([1, 0, 0])    # 红色表示查询点neighbors_pcd = o3d.geometry.PointCloud()   # 创建一个包含最近邻点的点云
neighbors_pcd.points = o3d.utility.Vector3dVector(neighbor_points)
neighbors_pcd.paint_uniform_color([0, 0, 1])  # 蓝色表示邻居点o3d.visualization.draw_geometries([query_pcd, neighbors_pcd, pcd],window_name="Radius Search Result",width=1600, height=1200,point_show_normal=False)  # 可视化原始点云、查询点和邻居点
# -----可视化查询点和找到的邻居-----

o3d.geometry.KDTreeFlann.search_hybrid_vector_3d（混合搜索函数）

结合了 K-近邻搜索 (KNN) 和 半径搜索 (Radius Search) 的优点。
函数原型

num_found, indices, sqr_distances = kdtree.search_hybrid_vector_3d(query, radius, max_nn)

参数	参数说明
query (List[float],numpy.ndarray)	查询点的三维坐标 [x, y, z]，可以是原始点云中的一个点，也可以是空间中的任意一点。
radius (float)	搜索的半径，所有距离小于或等于此半径的点都会被找到。
max_nn (int)	在半径 radius 内最多返回的邻居点数量，即使半径内有更多点，也只返回最接近的 max_nn 个。

返回值	返回值说明
num_found (int)	实际找到的邻居数量。数量是 radius 内的点数和 max_nn 之间的较小值。
indices (List[int])	找到的所有在半径内的邻居点的索引。这些索引可用于访问原始点云中的对应点、颜色、法向量等属性。
sqr_distances (List[float])	查询点到每个找到的对应邻居点的平方欧几里得距离列表。注意：返回的是距离的平方，而不是原始距离。

示例：

import open3d as o3d    # 导入Open3D库
import numpy as np
pcd = o3d.io.read_point_cloud("tooth.ply")   # 读取点云数据
pcd.paint_uniform_color([1.0, 1.0, 0.0])    # 设置颜色
kdtree = o3d.geometry.KDTreeFlann(pcd)  # 构建KD树
query_point = pcd.points[0]  # 定义一个查询点 (这里以点云的第一个点为例),也指定任意的[x,y,z] 坐标
radius = 5      # 设置要搜索的半径大小
max_nn = 500     # 设置在半径内最多返回的邻居数量
[num_found, indices, sqr_distances] = kdtree.search_hybrid_vector_3d(query_point, radius, max_nn)   # 执行混合搜索
print(f"在点云中找到了 {num_found} 个最近邻点。")
print(f"这些点在原始点云中的索引为: {indices}")
print(f"到查询点的平方距离为: {sqr_distances}")
distances = np.sqrt(sqr_distances)  # 计算实际距离
print(f"到查询点的实际距离为: {distances}")
neighbor_points = np.asarray(pcd.points)[indices]   # 获取最近邻点的坐标
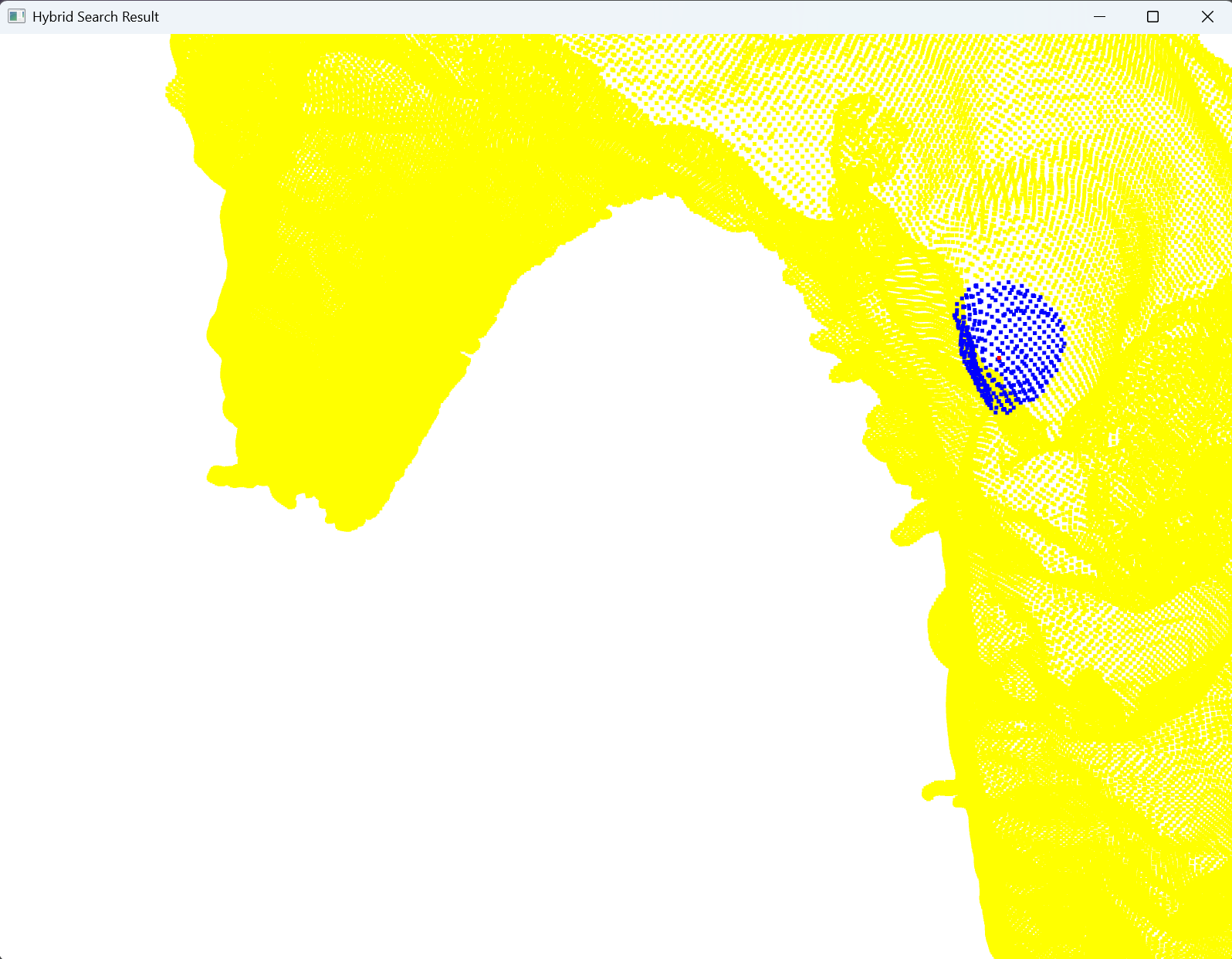
print(f"最近邻点的坐标为:\n{neighbor_points}")# -----可视化查询点和找到的邻居-----
query_pcd = o3d.geometry.PointCloud()   # 创建一个包含查询点的点云
query_pcd.points = o3d.utility.Vector3dVector([query_point])
query_pcd.paint_uniform_color([1, 0, 0])    # 红色表示查询点neighbors_pcd = o3d.geometry.PointCloud()   # 创建一个包含最近邻点的点云
neighbors_pcd.points = o3d.utility.Vector3dVector(neighbor_points)
neighbors_pcd.paint_uniform_color([0, 0, 1])  # 蓝色表示邻居点o3d.visualization.draw_geometries([query_pcd, neighbors_pcd, pcd],window_name="Hybrid Search Result",width=1600, height=1200,point_show_normal=False)  # 可视化原始点云、查询点和邻居点
# -----可视化查询点和找到的邻居-----

---

总结

o3d.geometry.Octree 主要用于点云的层次化空间划分和多分辨率表示，o3d.geometry.KDTreeFlann 则是专门为高效空间查询设计的工具。