当前位置：首页 > news >正文

排序知识总结

news 2025/8/9 5:42:54

排序的概念及引用

排序是使一串记录，按照某个关键字的大小，递增或递减排列起来的操作

稳定性：相同关键字排序前后相对顺序不变

内部排序：数据元素全部放在内存中排序

外部排序：数据太多不能同时放到内存中，根据排序的过程要求能在内外存之间移动数据的排序

常见的排序算法

插入排序

基本思想：类比扑克牌接牌

时间复杂度0（N^2）数据越有序，直接插入排序越快

空间复杂度0（1）

稳定性：稳定（如果一个排序是稳定的，那么他也可以实现为不稳定的）

  public static void insertSort(int[] array){for (int i = 1; i <array.length ; i++) {int tmp=array[i];int j=i-1;for (;j>=0;j--){if(array[j]>tmp){array[j+1]=array[j];}else{array[j+1]=tmp;break;}}array[j+1]=tmp;}}

希尔排序（缩小增量排序）

基本思想：先选定一个整数，把待排序的文件中所有记录分为多个组，所有距离为指定距离的分在同一个组，并对每组内的记录进行排序，然后重复上述分组和排序的工作，当达到1时，所有记录在同一组内排序

跳跃式分组：大的数据靠后，小的数据靠前

分组排序--->插入排序，组内进行插入排序

缩小增量--->数据少，数据无序；数据多，数据有序

当增量大于1时都是预排序

空间复杂度为0（1）时间复杂度为n^(1.3-1.5）来记忆

不稳定的

 public static void shellSort(int[] array){int gap= array.length;while(gap>1){gap/=2;shell(array,gap);}}private static void shell(int[] array, int gap) {for(int i=gap;i<array.length;i++){int tmp=array[i];int j=i-gap;for(;j>=0;j-=gap){if(array[j]>tmp){array[j+gap]=array[j];}else{array[j+gap]=tmp;break;}}array[j+gap]=tmp;}}

选择排序

基本思想：每次从数据中选最大/最小的排

时间复杂度：O(N^2) 空间复杂度：O（1）稳定性：不稳定的排序

public static void selectSort1(int[]array){for (int i = 0; i < array.length; i++) {int minIndex=i;for ( int j=i+1; j <array.length ; j++) {if(array[j]<array[minIndex]){minIndex=j;}}swap(array,minIndex,i);}}public static void swap(int[] array, int x, int y) {int tmp=array[x];array[x]=array[y];array[y]=tmp;}

思路二：左右同时找。left=0，right=arr.length-1 有一个min 有一个max初始为left

int i=left+1，找最大和最小，然后交换

 public static void selectSort(int[]arr){int left=0;int right=arr.length-1;while(left<right){int min=left;int max=left;for (int i = left+1; i <=right ; i++) {if(arr[i]>arr[max]){max=i;}if(arr[i]<arr[min]){min=i;}}swap(arr,min,left);if(max==left){max=min;}swap(arr,right,max);right--;left++;}}

堆排序

思路：创建大根堆 0下标和end交换

稳定性：不稳定

时间复杂度0（n*logN）空间复杂度0（1）

public static void heapSort(int[]arr){createHeap(arr);int end=arr.length-1;while(end>0){swap(arr,0,end);siftDown(arr,0,end);end--;}}private static void createHeap(int[] arr) {for(int parent=(arr.length-1-1)/2;parent>=0;parent--){siftDown(arr,parent,arr.length);}}public static void siftDown(int[] arr, int parent, int end) {int child=parent*2+1;while(child<end){if(child+1<end&&arr[child]<arr[child+1]){child=child+1;}if(arr[child]>arr[parent]){swap(arr,parent,child);parent=child;child=parent*2+1;}else{break;}}}

交换排序

冒泡排序

基本思想：比较交换

时间复杂度0（N^2）优化后可能会达到O(N)

空间复杂度O（1）

稳定的排序

优化：1.int j=arr.length-1-i；2.设置一个flg如果未交换break

 public static void bubbleSort(int[]arr){for (int i = 0; i < arr.length; i++) {boolean flg=false;for (int j = 0; j < arr.length-1-i; j++) {if(arr[j]>arr[j+1]){swap(arr,j,j+1);flg=true;}}if(!flg){break;}}}

快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，从后边开始找到比基准小的停下来，从前面开始找到比基准大的停下来直至两个相遇，相遇的即为新基准，找到基准后再分两边找，类似二叉树

时间复杂度：当给定1，2,3,4......有序情况下0（n^2）

当每次都能均匀分开时0(logN)

空间复杂度：最坏单分支树0（N）最好情况：0（logN）完全二叉树

稳定性：不稳定的排序

挖坑法（做题优先考虑的思想）：先把left（0）拿出，0坐标空出即为坑，从后边找比基准小的直接填坑，再从前边找比基准大的挖坑

前后指针法：两个指针prev和cur

prev=legft，cur=left+1

一前一后走，找到比基准小的进行交换

优化思路：减少他的递归次数

1.三数取中法（left，right，mid找到这三个数据中）

2.直接插入法（针对一定范围）二叉树越深，递归次数越多，可以在最后几层直接插入排序（因为数据少且趋于有序）

public static void quickSort(int[]arr){if(arr==null){return;}quick(arr,0,arr.length-1);}public static void quick(int[]arr,int begin,int end){if(begin>=end){return;}if(begin+end-1<=7){insertSortRange(arr,begin,end);}int midIndex=getMid(arr,begin,end);swap(arr,begin,midIndex);int pivot=partition(arr,begin,end);quick(arr,0,pivot-1);quick(arr,pivot+1,end);}public static int getMid(int[]arr,int begin,int end){int mid=(begin+end)/2;if(arr[begin]>arr[end]){if(arr[mid]>arr[begin]){return begin;}else if(arr[mid]>arr[end]){return mid;}else{return end;}}else{if(arr[mid]>arr[end]){return end;}else if(arr[mid]>arr[begin]){return mid;}else{return begin;}}}public static void insertSortRange(int[]arr,int begin,int end){for (int i = begin+1;i<=end;i++){int tmp=arr[i];int j=i-1;for(;j<=end;j--){if(arr[j]>tmp){arr[j+1]=arr[j];}else{arr[j+1]=tmp;break;}}arr[j+1]=tmp;}}public static int partition2(int[]arr,int left,int right){int prev=left;int cur=prev+1;while(cur<=right){if(arr[cur]<arr[left]&&arr[++prev]!=arr[cur]){swap(arr,prev,cur);}cur++;}swap(arr,prev,left);return  prev;}public static int partition(int[]arr,int left,int right){int tmp=arr[left];while(left<right){while(left<right&&arr[right]>=tmp){right--;}arr[left]=arr[right];while(left<right&&arr[left]<=tmp){left++;}arr[right]=arr[left];}arr[left]=tmp;return left;}public static int partitionHoare(int[]arr,int left,int right){int tmp=arr[left];int tmpLeft=left;while(left<right){while(left<right&&arr[right]>=tmp){right--;}while(left<right&&arr[left]<=tmp){left++;}swap(arr,left,right);}swap(arr,left,tmpLeft);return left;}public static void swap(int[]arr,int i,int j){int tmp=arr[i];arr[i]=arr[j];arr[j]=tmp;}

快速排序的非递归实现：利用的是栈

找到基准如果基准左右有两个元素及以上再次找基准只要栈不为空，先找左再找右

 public static void quickSort(int[]arr){if(arr==null){return;}quickNor(arr,0,arr.length-1);}public static void quickNor(int[]arr,int start,int end){Deque<Integer> stack=new ArrayDeque<>();int pivot=partition(arr,start,end);if(pivot>start+1){stack.push(start);stack.push(pivot-1);}if(pivot<end-1){stack.push(pivot+1);stack.push(end);}while(!stack.isEmpty()){end=stack.pop();start=stack.pop();pivot=partition(arr,start,end);if(pivot>start+1){stack.push(start);stack.push(pivot-1);}if(pivot<end-1){stack.push(pivot+1);stack.push(end);}}}

归并排序（mergeSort）

建立在归并操作的一种有效的排序算法，归并排序是最常用的外部排序

分解+合并

时间复杂度0（NlogN）空间复杂度0（N）稳定性：稳定

如图为归并排序的拆分过程

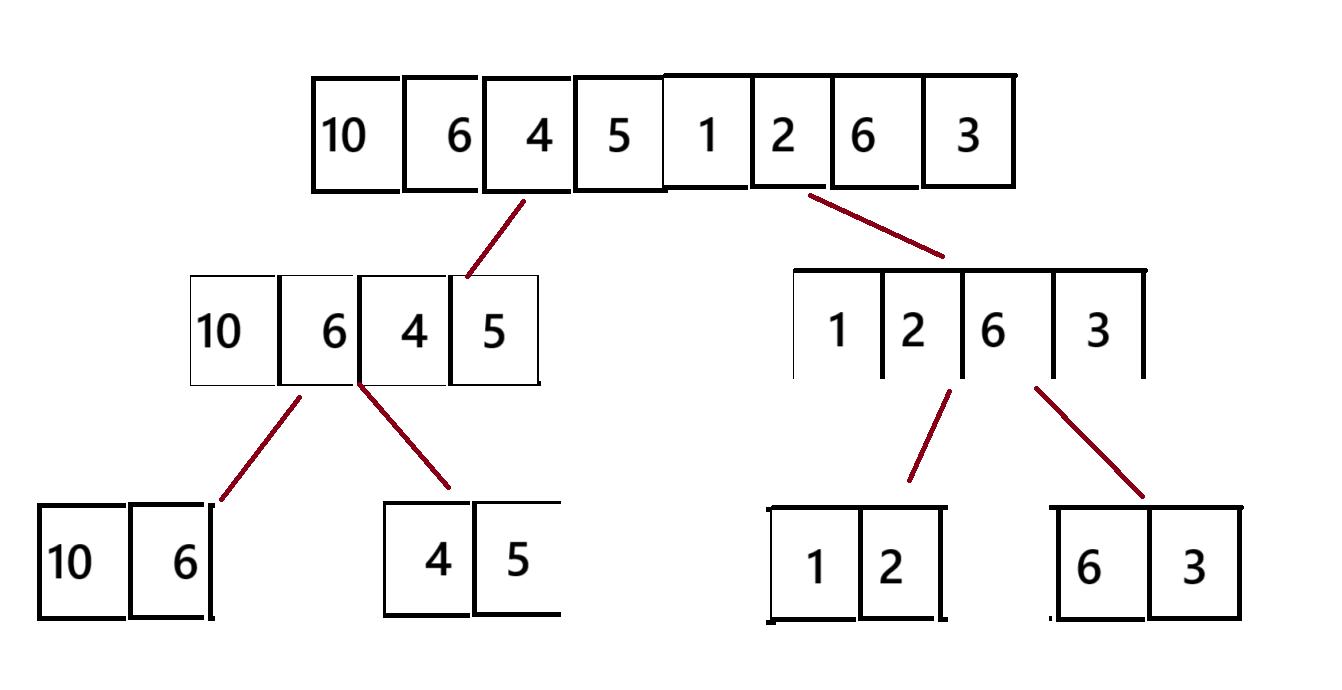
public static void mergeSort(int[]arr){mergeSortMap(arr,0,arr.length-1);}public static void mergeSortMap(int[]arr,int left,int right){if(left>=right){return;}int mid=(left+right)/2;mergeSortMap(arr,left,mid);mergeSortMap(arr,mid+1,right);merge(arr,left,mid,right);}public static void merge(int[]arr,int left,int mid,int right){int[]tmp=new int[right-left+1];int k=0;int s1=left;int s2=mid+1;while (s1 <= mid && s2 <= right) {if(arr[s1] <= arr[s2]) {tmp[k++] = arr[s1++];}else {tmp[k++] = arr[s2++];}}while (s1 <= mid) {tmp[k++] = arr[s1++];}while (s2 <= right) {tmp[k++] = arr[s2++];}//可以保证tmp数组 是有序的for (int i = 0; i < k; i++) {arr[i+left] = tmp[i];}}
}

非递归的归并排序

gap=1一个一个有效

gap=2两个两个有效....gap>=len有序

public static void merge(int[]arr,int left,int mid,int right){int[]tmp=new int[right-left+1];int s1=left;int s2=mid+1;int k=0;while(s1<=mid&&s2<=right){if(arr[s1]<=arr[s2]){tmp[k++]=arr[s1++];}else{tmp[k++]=arr[s2++];}}while(s1<=mid){tmp[k++]=arr[s1++];}while(s2<=right){tmp[k++]=arr[s2++];}for (int i = 0; i <k ; i++) {arr[i+left]=tmp[i];}}public static void mergeSortNor(int[]arr){int gap=1;while(gap<arr.length){for (int i = 0; i < arr.length; i = i + gap * 2) {int left = i;int mid = left + gap - 1;if(mid >= arr.length) {mid = arr.length-1;}int right = mid + gap;if(right >= arr.length) {right = arr.length-1;}merge(arr,left,mid,right);}gap *= 2;}}

其他非基于比较的排序

计数排序（鸽巢原理）

是对哈希直接地址法的变形应用

步骤：1.统计相同元素的次数

2.根据统计的结果将序列回收到原来的序列中

public static void countSort(int[] array) {int maxVal = array[0];int minVal = array[0];for (int i = 1; i < array.length; i++) {if(array[i] < minVal) {minVal = array[i];}if(array[i] > maxVal) {maxVal = array[i];}}int len = maxVal - minVal + 1;int[] count = new int[len];for (int i = 0; i < array.length; i++) {int index = array[i];count[index-minVal]++;}int index = 0;for (int i = 0; i < count.length; i++) {while (count[i] != 0) {array[index] = i+minVal;index++;count[i]--;}}}

桶排序

划分多个范围相同的区间，每个子区间自排序，最后合并。

是计数排序的扩展版本，计数排序可以看成每个桶只存储相同元素，而桶排序每个桶存储一定范围的元素，通过映射函数，将待排序数组中的元素映射到各个对应的桶中，对每个桶中的元素进行排序，最后将非空桶中的元素逐个放入原序列中。

桶排序需要尽量保证元素分散均匀，否则当所有数据集中在同一个桶中时，桶排序失效。

public static void bucketSort(int[] arr){// 计算最大值与最小值int max = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int i = 0; i < arr.length; i++){max = Math.max(max, arr[i]);min = Math.min(min, arr[i]);}// 计算桶的数量int bucketNum = (max - min) / arr.length + 1;ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());}// 将每个元素放入桶for(int i = 0; i < arr.length; i++){int num = (arr[i] - min) / (arr.length);bucketArr.get(num).add(arr[i]);}// 对每个桶进行排序for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));}// 将桶中的元素赋值到原序列int index = 0;for(int i = 0; i < bucketArr.size(); i++){for(int j = 0; j < bucketArr.get(i).size(); j++){arr[index++] = bucketArr.get(i).get(j);}}  
}