[优选算法专题一双指针——两数之和](双指针和哈希表)
题目链接
LeetCode两数之和
题目描述

题目解析
注意:前提条件:输入的数组numbers是已排序的。
核心思路:双指针法
利用数组已排序的特性,通过两个指针从两端向中间移动,快速定位符合条件的两个数,时间复杂度为O(n)(n 为数组长度),空间复杂度为O(1),比哈希表解法更优。
具体步骤:
-
初始化指针:
left指针指向数组起始位置(下标 0)。right指针指向数组末尾位置(下标numbers.size()-1)。
-
循环查找目标和:
- 计算两指针指向元素的和
sum = numbers[left] + numbers[right]。 - 若
sum > target:说明右侧元素过大,将right指针左移(right--),减小总和。 - 若
sum < target:说明左侧元素过小,将left指针右移(left++),增大总和。 - 若
sum == target:找到符合条件的两个元素,返回它们的下标(注意 + 1,因为题目要求从 1 开始计数)。
- 计算两指针指向元素的和
-
边界处理:
- 若循环结束仍未找到(理论上题目保证有解,此步可省略),返回
{-1, -1}。
- 若循环结束仍未找到(理论上题目保证有解,此步可省略),返回
示例说明:
假设输入:numbers = [2, 7, 11, 15],target = 9。
- 初始
left=0(值 2),right=3(值 15),sum=17 > 9→right--(指向 11)。 - 新
sum=2+11=13 > 9→right--(指向 7)。 - 新
sum=2+7=9 == target→ 返回{0+1, 1+1} = {1, 2}。
完整代码
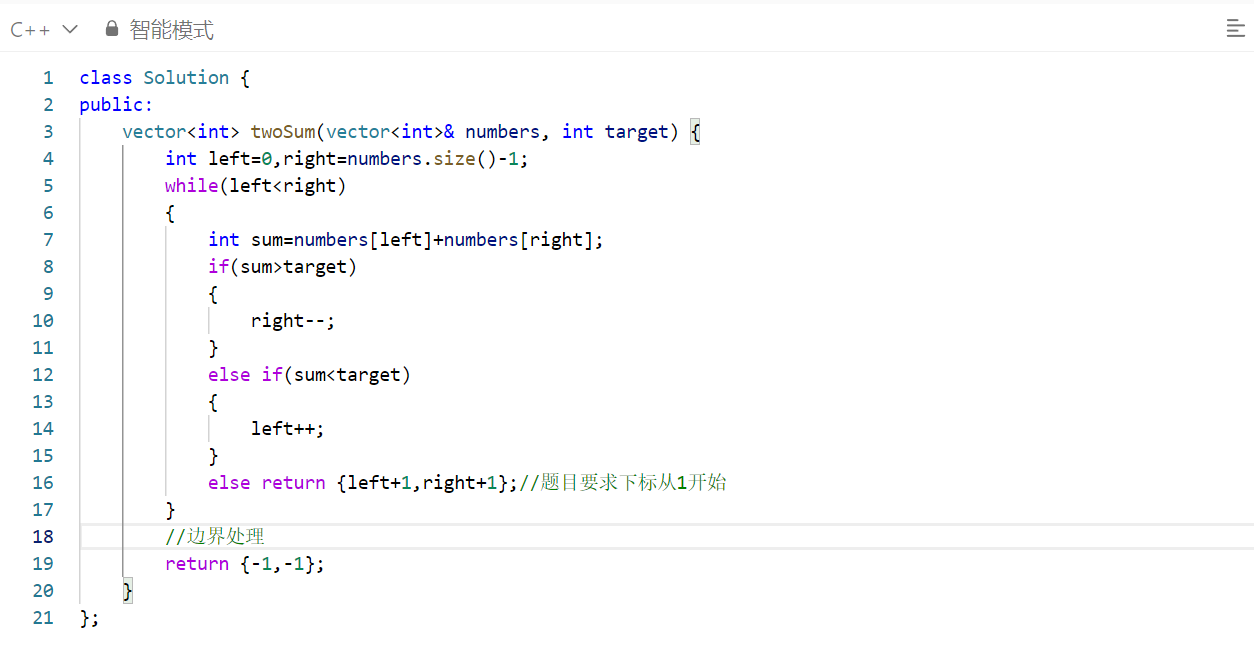
复杂度分析
1. 时间复杂度:O (n)
- 分析:算法使用双指针(
left和right)从数组两端向中间移动,每次循环仅移动一个指针,直到两指针相遇(left >= right)。 - 最坏情况:两个指针总共移动的次数不会超过数组长度
n(例如,目标值需要最小元素和最大元素相加时,指针从两端移动到相遇,总步数为n级)。 - 结论:时间复杂度为 O(n),其中
n是数组numbers的长度。
2. 空间复杂度:O (1)
- 分析:算法仅使用了常数个额外变量(
left、right、sum),没有使用与输入规模相关的额外空间(如哈希表、数组等)。 - 结论:空间复杂度为 O(1),属于原地(in-place)算法。
如果是无序的,这里我们可以使用哈希表来解决!
哈希表法(无序)
解法思路:哈希表(空间换时间)
这个解法的核心是利用 哈希表(unordered_map) 存储已经遍历过的元素及其下标,通过一次遍历就能找到答案,避免了暴力解法的二次循环。
具体逻辑:
- 遍历数组中的每个元素
nums[j](j是当前下标) - 计算与当前元素互补的数值:
complement = target - nums[j] - 检查哈希表中是否存在
complement:
- 若存在,说明之前已经遍历过值为
complement的元素(下标为i),则i和j就是答案 - 若不存在,将当前元素
nums[j]和其下标j存入哈希表,继续遍历
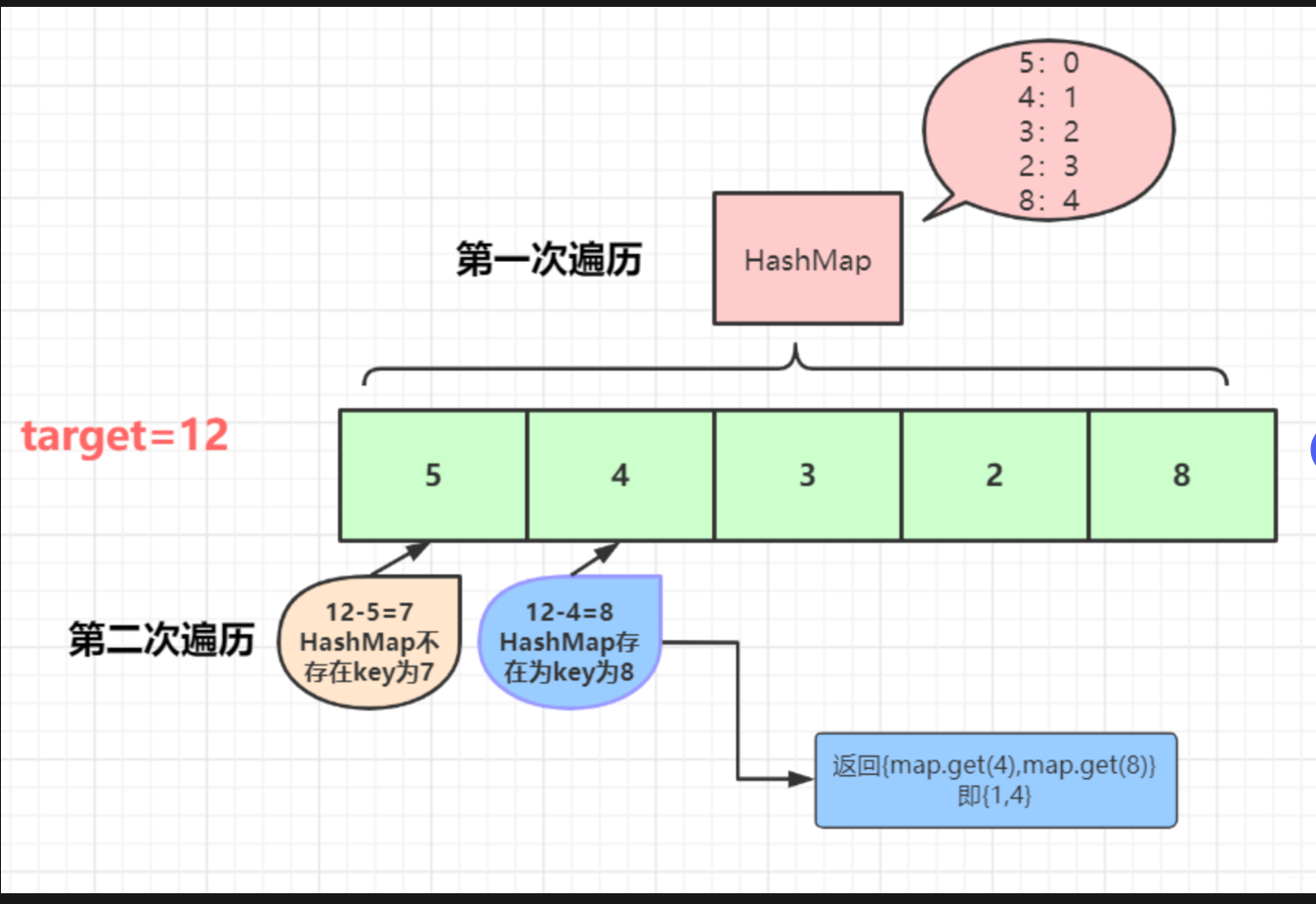
代码执行流程(分步演示)
-
我们以
nums = [5, 4, 3, 2, 8]且target = 12为例,详细演示代码的执行过程。预期结果
在这个例子中,数组中 4 + 8 = 12,对应的下标是
1和4,因此最终应该返回[1, 4]。代码执行步骤拆解
我们按照代码的执行顺序,一步步分析哈希表的变化和每轮循环的操作:
-
初始化:
- 创建空哈希表
idx = {}(用于存储已遍历元素的值和下标) - 循环变量
j从0开始
- 创建空哈希表
-
第一轮循环(j=0,当前元素 nums [0]=5):
- 计算互补值:
complement = target - nums[j] = 12 - 5 = 7 - 检查哈希表
idx中是否存在7:此时哈希表为空,未找到 - 将当前元素存入哈希表:
idx[5] = 0(现在哈希表为{5:0}) - 继续下一轮循环
- 计算互补值:
-
第二轮循环(j=1,当前元素 nums [1]=4):
- 计算互补值:
complement = 12 - 4 = 8 - 检查哈希表
idx中是否存在8:当前哈希表只有5,未找到 - 将当前元素存入哈希表:
idx[4] = 1(现在哈希表为{5:0, 4:1}) - 继续下一轮循环
- 计算互补值:
-
第三轮循环(j=2,当前元素 nums [2]=3):
- 计算互补值:
complement = 12 - 3 = 9 - 检查哈希表
idx中是否存在9:哈希表中只有5和4,未找到 - 将当前元素存入哈希表:
idx[3] = 2(现在哈希表为{5:0, 4:1, 3:2}) - 继续下一轮循环
- 计算互补值:
-
第四轮循环(j=3,当前元素 nums [3]=2):
- 计算互补值:
complement = 12 - 2 = 10 - 检查哈希表
idx中是否存在10:哈希表中没有10,未找到 - 将当前元素存入哈希表:
idx[2] = 3(现在哈希表为{5:0, 4:1, 3:2, 2:3}) - 继续下一轮循环
- 计算互补值:
-
第五轮循环(j=4,当前元素 nums [4]=8):
- 计算互补值:
complement = 12 - 8 = 4 - 检查哈希表
idx中是否存在4:此时哈希表中存在4,对应的下标是1(即idx[4] = 1) - 找到答案,直接返回
[1, 4](互补元素的下标1和当前元素的下标4) - 程序结束
- 计算互补值:
-
代码细节解析
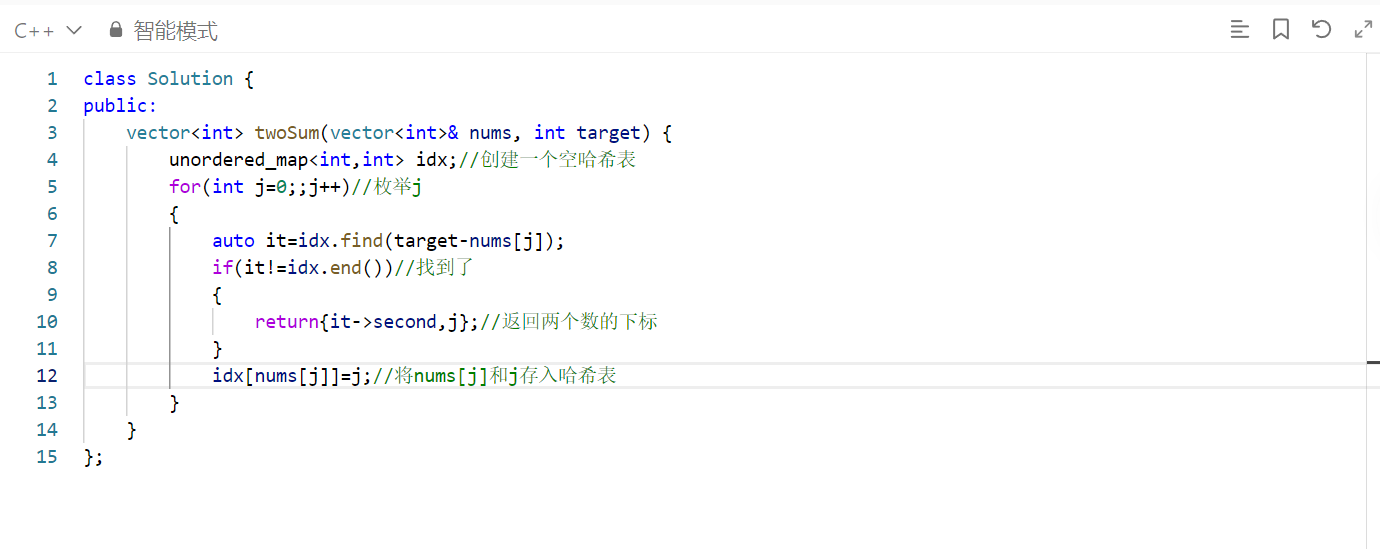
完整代码
-
哈希表的作用:
unordered_map<int, int> idx中,key 是数组元素的值,value 是该元素的下标- 哈希表的查找操作是 O(1) 时间复杂度,比数组查找(O (n))快得多
-
循环设计:
- 原代码中的
for (int j = 0; ; j++)其实隐含了j < nums.size()的条件(题目保证有解,所以一定会在循环内返回) - 标准写法应该是
for (int j = 0; j < nums.size(); j++),更严谨
- 原代码中的
-
避免重复使用元素:
- 因为我们是先检查哈希表,再将当前元素存入哈希表,所以哈希表中永远只包含「当前元素之前的元素」
- 这就保证了不会出现「自己和自己相加」的情况(例如
nums = [3,3]时,第一个 3 存入哈希表后,第二个 3 才会查找并命中)
-
返回值:
- 题目保证有且仅有一个解,所以循环内一定会找到答案并返回
- 理论上不需要最后的
return {},但为了满足 C++ 语法(函数必须有返回值),通常会加上
时间复杂度为 O(n)
