机器学习通关秘籍|Day 04:梯度下降的概念原理、手动实现梯度下降
目录
一、梯度下降
1、梯度下降概念
2、梯度下降步骤
3、梯度下降公式
4、学习率
二、梯度下降算法
1、批量梯度下降BGD(Batch Gradient Descent)
2、随机梯度下降SGD(Stochastic Gradient Descent)
3、小批量梯度下降MBGD(Mini-Batch Gradient Descent)
4、总结对比
三、手动实现梯度下降
1、手动实现简单的梯度下降
2、随机梯度下降
3、小批量梯度下降
四、总结
一、梯度下降
在机器学习和深度学习中,梯度下降 是一种非常重要的优化算法,用于 最小化损失函数,从而找到模型参数的最佳值。无论是线性回归、神经网络还是其他复杂的模型,梯度下降都是训练过程的核心。
1、梯度下降概念
在前面的博客中我们提到,用高斯的最小二乘法求得最优解。使用正规方程 ![]() 求解要求X的特征维度
求解要求X的特征维度![]() 不能太多,逆矩阵运算时间复杂度为O(n^3) , 也就是说如果特征x的数量翻倍,计算时间就是原来的2^3倍,8倍太恐怖了,假设2个特征1秒,4个特征8秒,8个特征64秒,16个特征512秒,而往往现实生活中的特征非常多,尤其是大模型,运行时间太长了。
不能太多,逆矩阵运算时间复杂度为O(n^3) , 也就是说如果特征x的数量翻倍,计算时间就是原来的2^3倍,8倍太恐怖了,假设2个特征1秒,4个特征8秒,8个特征64秒,16个特征512秒,而往往现实生活中的特征非常多,尤其是大模型,运行时间太长了。
所以 正规方程求出最优解并不是机器学习和深度学习常用的手段,梯度下降算法更常用
什么是梯度下降?
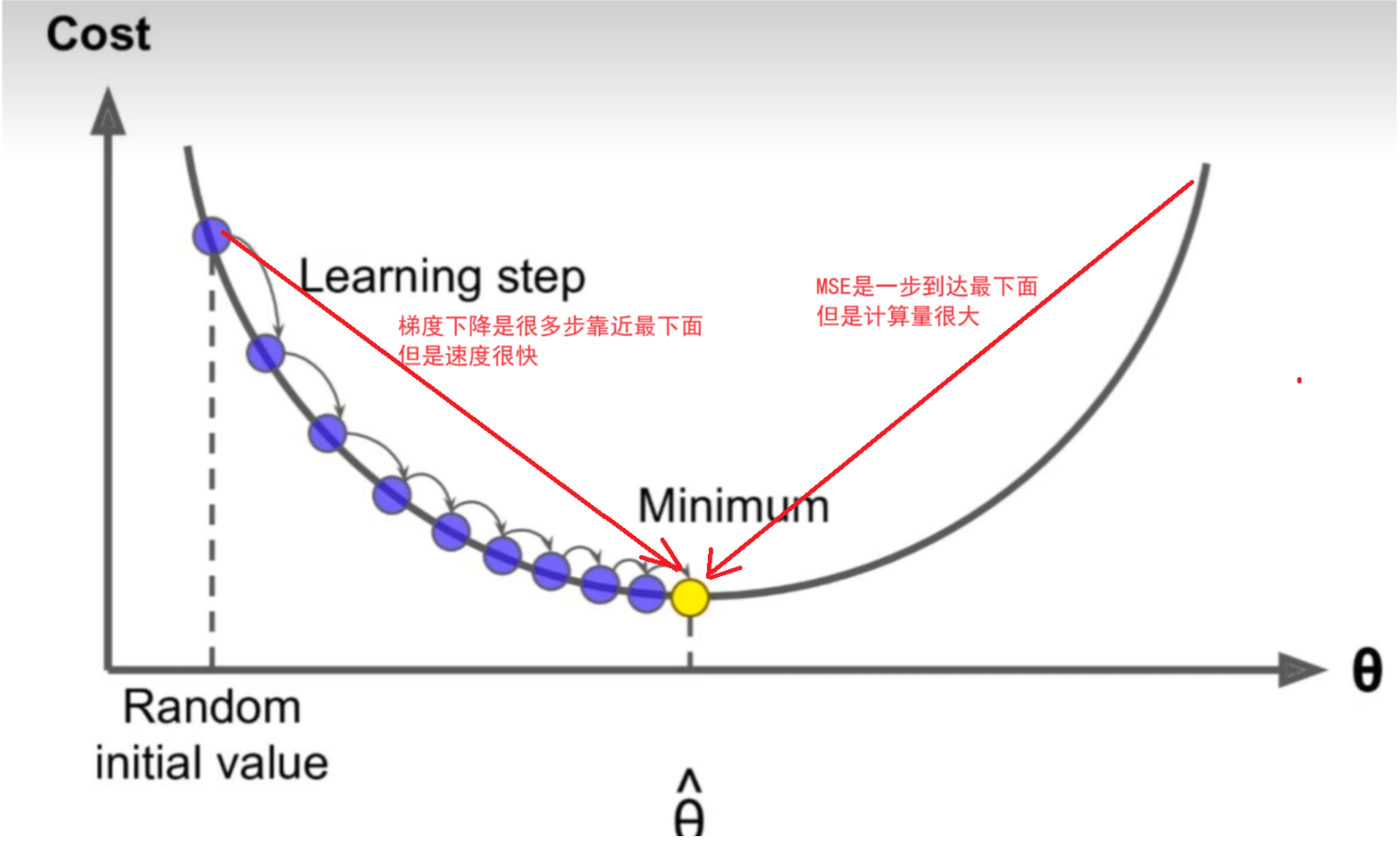
梯度下降是一种迭代优化算法,用于寻找函数的最小值(或最大值)。其核心思想是沿着目标函数的负梯度方向更新参数,从而逐步逼近最优解。梯度是函数在某一点上的变化率,表示函数在该点上升最快的方向。因此,负梯度方向就是函数下降最快的方向。
假设你是一名登山者,站在一座山的山顶,目标是找到山脚下的最低点。你可以通过以下步骤实现:
-
观察地形:看看周围哪个方向的坡度最陡。
-
沿最陡方向移动:朝着坡度最陡的方向迈出一小步。
-
重复上述过程:不断重复观察和移动,直到到达最低点。
在机器学习中,损失函数就像这座山,参数 θ 就是你当前的位置,而梯度就是告诉你“坡度最陡的方向”。通过不断沿着负梯度方向更新参数,最终可以找到损失函数的最小值。
在机器学习中,梯度表示损失函数对于模型参数的偏导数。具体来说,对于每个可训练参数,梯度告诉我们在当前参数值下,沿着每个参数方向变化时,损失函数的变化率。通过计算损失函数对参数的梯度,梯度下降算法能够根据梯度的信息来调整参数,朝着减少损失的方向更新模型,从而逐步优化模型,使得模型性能更好。
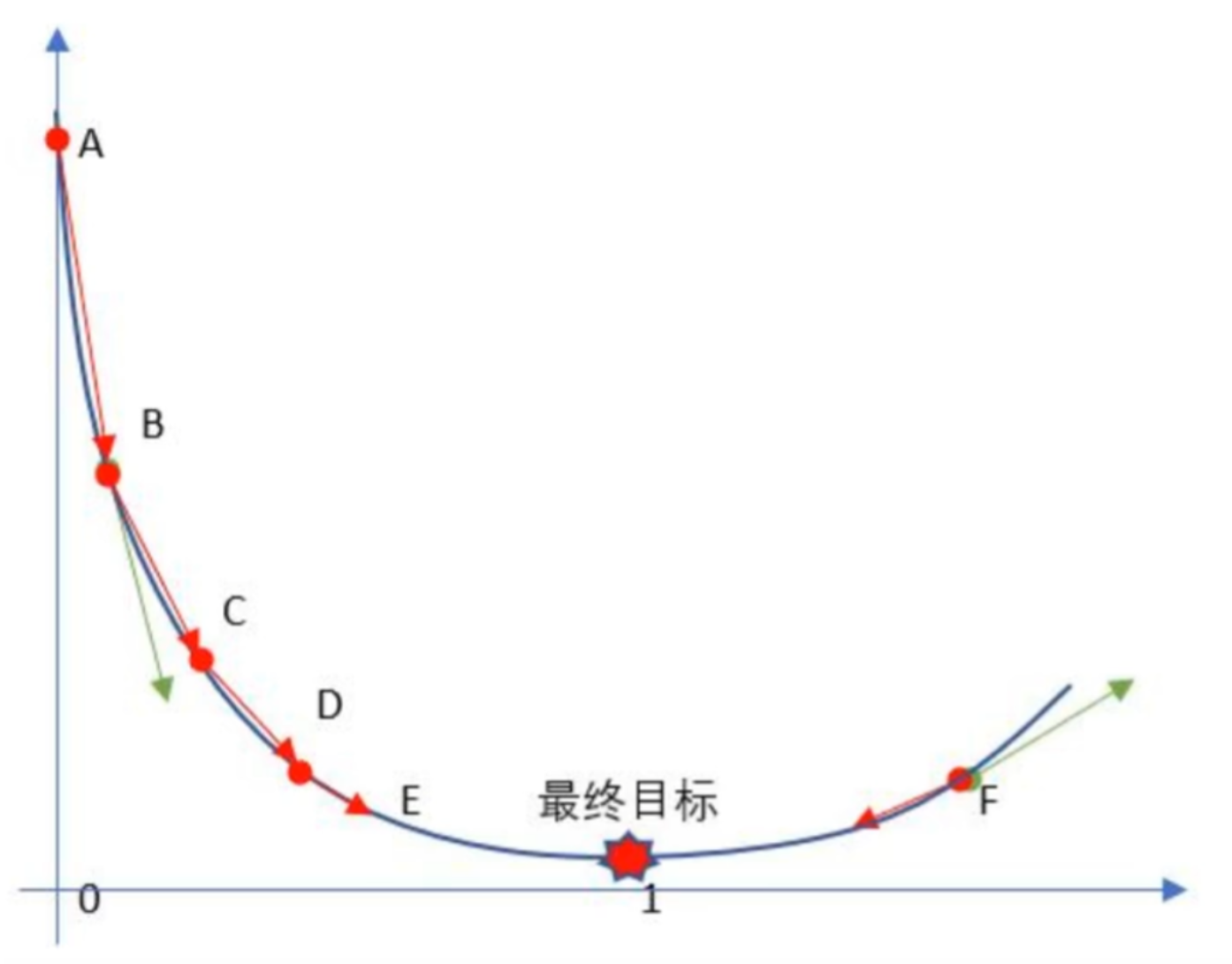
在 ![]() 这个一元二次方程中,损失函数对于参数 w 的梯度就是关于 w 点的切线斜率。梯度下降算法会根据该斜率的信息来调整参数 w,使得损失函数逐步减小,从而找到使得损失最小化的参数值,优化模型的性能。
这个一元二次方程中,损失函数对于参数 w 的梯度就是关于 w 点的切线斜率。梯度下降算法会根据该斜率的信息来调整参数 w,使得损失函数逐步减小,从而找到使得损失最小化的参数值,优化模型的性能。
梯度下降法(Gradient Descent)是一个算法,但不是像多元线性回归那样是一个具体做回归任务的算法,而是一个非常通用的优化算法来帮助一些机器学习算法求解出最优解,所谓的通用就是很多机器学习算法都是用梯度下降,甚至深度学习也是用它来求解最优解。 所有优化算法的目的都是期望以最快的速度把模型参数W求解出来,梯度下降法就是一种经典常用的优化算法。
2、梯度下降步骤
步骤 1:定义模型与损失函数
首先,我们需要明确要优化的模型和目标函数。
-
模型假设:例如线性回归模型
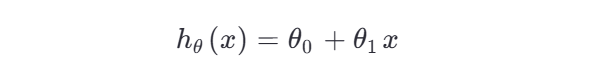

-
损失函数:通常使用均方误差(Mean Squared Error, MSE)
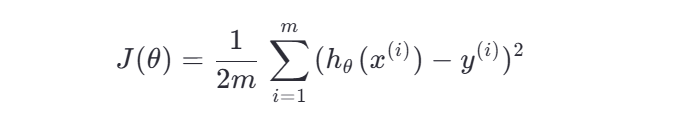

📌 为什么需要损失函数?
它衡量了模型预测值与真实值之间的差距,我们的目标就是通过调整参数 θ 来最小化这个差距。
步骤 2:初始化参数
在开始迭代之前,需要对模型参数进行初始化。
-
通常将 θ0 和 θ1 初始化为小的随机数或零。
-
示例:
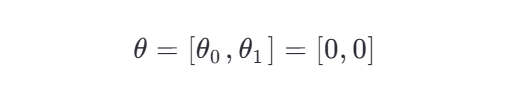
⚠️ 注意:虽然初始化为 0 在简单模型中可行,但在神经网络中应避免全零初始化,否则会导致对称性问题。
步骤 3:计算梯度(偏导数)
对损失函数 J(θ) 分别对每个参数求偏导,得到梯度向量。
以 MSE 损失为例,其关于 θ0 和 θ1 的偏导数为:
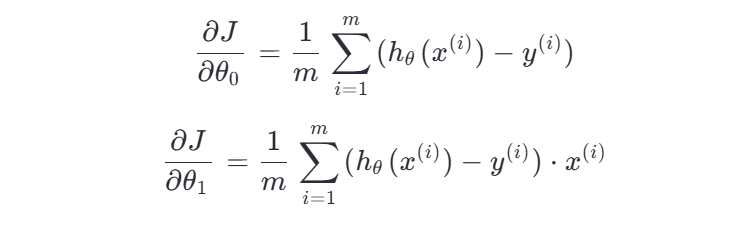
🧠 通俗理解:
这些偏导数告诉我们:如果稍微改变 θ0 或 θ1 ,损失会如何变化。梯度指明了“上坡”的方向,所以我们取负梯度来“下坡”。
步骤 4:更新参数
使用梯度下降更新公式,沿负梯度方向调整参数:
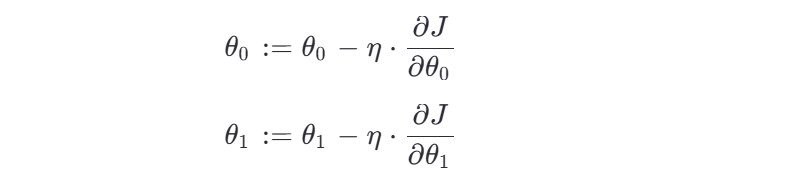
🔁 这个过程是迭代进行的,每一轮都重新计算梯度并更新参数。
步骤 5:判断是否收敛
设置停止条件,常见的有以下几种:
-
达到最大迭代次数(如 1000 轮)
-
损失函数的变化小于某个阈值(如
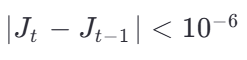 )
) -
梯度接近零(说明已到达极小点附近)
✅ 一旦满足任一条件,算法停止,输出最终的 θ 值。
💡 举个生活化例子:调节热水器温度
想象你要洗澡,热水器的温度由两个旋钮控制:θ0 (基础水温)、θ1 (热水比例)。你感觉当前水温太冷,想调到最舒服的状态。
| 步骤 | 对应梯度下降操作 |
|---|---|
| 你觉得“有点冷” | 损失函数告诉你偏离目标 |
| 你试探性地转一下热水旋钮 | 计算梯度,知道哪个方向更“热” |
| 发现变烫了,赶紧回调一点 | 学习率控制步长,避免过调 |
| 反复微调直到舒适 | 多次迭代逼近最优解 |
这就是梯度下降的直观体现:通过反馈不断调整,逐步逼近理想状态。
3、梯度下降公式
梯度下降的更新公式如下:
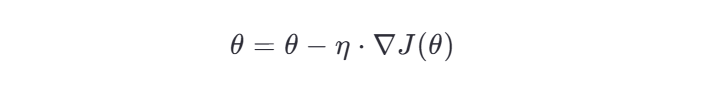
其中:
-
θ :模型参数
-
η :学习率(步长)
-
∇J(θ) :损失函数 J(θ) 关于参数 θ 的梯度
通俗解释:
-
θ :你的当前位置(参数)。
-
η :每一步迈多大(学习率)。
-
∇J(θ) :当前点的坡度方向(梯度)。
-
公式的意义:每次更新时,沿着坡度最陡的方向(负梯度方向)迈出一小步。
4、学习率
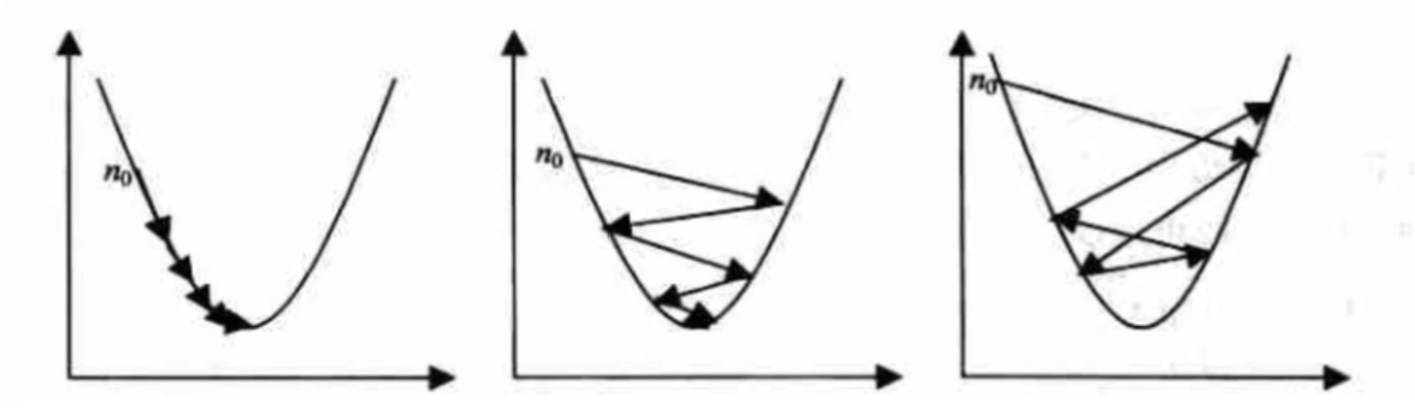
η很小时,可以保证收敛 较大的η,训练将震荡收敛 η过大,系统无法收敛
学习率 η 是梯度下降中的一个重要超参数,决定了每次迭代时参数更新的幅度。如果学习率过小,收敛速度会很慢;如果学习率过大,可能会导致振荡甚至无法收敛。因此,选择合适的学习率是梯度下降成功的关键。
通俗例子: 回到登山场景,学习率就像是你每一步迈的距离:
-
如果学习率太小(步子太小),你虽然不会偏离路线,但需要很长时间才能到达山脚。
-
如果学习率太大(步子太大),你可能会跨过最低点,甚至掉进坑里。
二、梯度下降算法
官方的梯度下降API常用有三种:
批量梯度下降BGD(Batch Gradient Descent)
小批量梯度下降MBGD(Mini-BatchGradient Descent)
随机梯度下降SGD(Stochastic Gradient Descent)
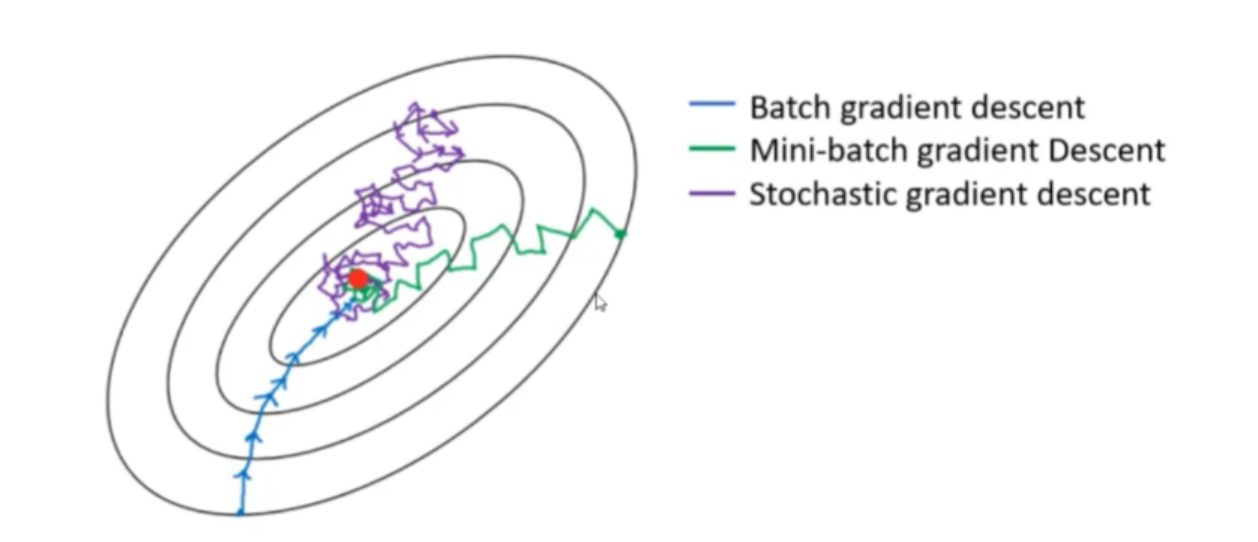
1、批量梯度下降BGD(Batch Gradient Descent)
(1)原理
-
定义:批量梯度下降使用整个训练集的数据来计算梯度,然后根据梯度更新模型参数。
-
公式:
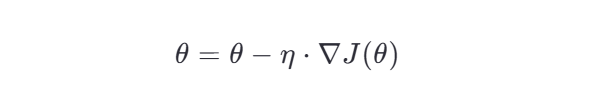
其中:
-
θ :模型参数
-
η :学习率(步长)
-
∇J(θ) :损失函数 J(θ) 对参数 θ 的梯度
-
J(θ) :损失函数,通常表示为所有样本的平均损失:
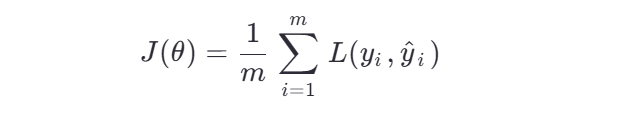
其中 m 是训练样本的数量,
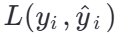 是单个样本的损失函数。
是单个样本的损失函数。
-
(2)优点
-
稳定性高:由于使用了整个数据集计算梯度,梯度的方向更准确,收敛路径较为平滑。
-
全局最优解的可能性大:在凸优化问题中,BGD 更有可能找到全局最优解。
-
适合小规模数据集:当数据量较小时,计算梯度的开销可以接受。
(3)缺点
-
计算效率低:每次迭代都需要遍历整个数据集,计算成本高,尤其在大数据集上表现不佳。
-
内存需求高:需要一次性加载整个数据集到内存中,不适合大规模数据场景。
-
不适用于在线学习:无法实时处理新数据。
2、随机梯度下降SGD(Stochastic Gradient Descent)
(1)原理
-
定义:SGD 每次迭代只使用一个随机样本计算梯度,而不是整个数据集。
-
公式:
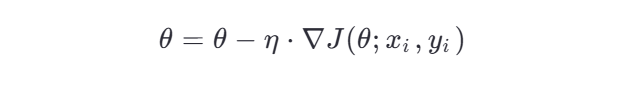
-
其中:
-
xi,yi :第 i 个样本的特征和标签。
-
∇J(θ;xi,yi) :基于单个样本的损失函数梯度。
(2)优点
-
计算效率高:每次迭代只需计算一个样本的梯度,计算速度快,适合大规模数据集。
-
内存需求低:无需一次性加载整个数据集,节省内存。
-
易于实现在线学习:可以实时处理新数据。
-
有助于跳出局部最优:由于噪声的存在,SGD 的路径更加“抖动”,可能有助于跳出局部最优解。
(3)缺点
-
收敛速度慢且不稳定:由于每次迭代仅使用一个样本,梯度方向可能存在较大偏差,导致收敛路径抖动。
-
难以达到精确的最优解:最终可能会在最优解附近震荡,而非精确收敛。
-
对学习率敏感:学习率的选择对性能影响很大,过大会导致发散,过小会导致收敛缓慢。
3、小批量梯度下降MBGD(Mini-Batch Gradient Descent)
(1)原理
-
定义:MBGD 是 BGD 和 SGD 的折中方案,每次迭代使用一个小批量(mini-batch)样本计算梯度。
-
公式:
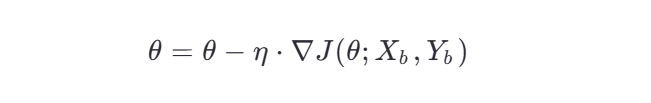
其中:
-
Xb,Yb :当前小批量样本的特征和标签。
-
∇J(θ;Xb,Yb) :基于小批量样本的损失函数梯度。
-
(2)优点
-
平衡计算效率和稳定性:相比 BGD,计算效率更高;相比 SGD,稳定性更好。
-
利用硬件加速:小批量计算可以充分利用 GPU 等硬件的并行计算能力。
-
适合大规模数据集:可以通过调整小批量大小,在计算效率和内存占用之间找到平衡。
(3)缺点
-
小批量大小的选择:需要根据具体问题调整小批量大小,过大或过小都会影响性能。
-
不如 BGD 稳定:由于每次迭代仅使用部分样本,梯度方向仍可能存在一定偏差。
4、总结对比
| 算法 | 计算方式 | 优点 | 缺点 |
|---|---|---|---|
| BGD | 使用整个数据集计算梯度 | 稳定性高,全局最优解可能性大 | 计算效率低,内存需求高 |
| SGD | 使用单个样本计算梯度 | 计算效率高,内存需求低,适合在线学习 | 收敛不稳定,难以达到精确最优解 |
| MBGD | 使用小批量样本计算梯度 | 平衡计算效率和稳定性,适合大规模数据 | 小批量大小选择困难 |
三、手动实现梯度下降
1、手动实现简单的梯度下降
(1)一个 w (特征)的梯度下降
代码示例:
import numpy as np
import matplotlib.pyplot as plt
# 生成数据集
data = np.array([[4.2, 3.8],[4.1, 2.7],[2.7, 2.4],[0.8, 1.0],[3.7, 2.8],[1.7, 0.9],[3.2, 2.9]])
x = data[:, 0]
y = data[:, 1]
# 定义损失函数
def loss(w):return 10 * (w ** 2) - 15.95 * w + 6.5
# 定义梯度函数
def g(w):return 20 * w - 15.95
# 随机初始化w
np.random.seed(0)
w = np.random.randint(10, 20)
t0 = 1
for i in range(1000):# 打印当前w的时候的模型预测的误差(均方差MSE)print("w:",w, "loss:",loss(w))a = t0/ (100+i)w = w - a * g(w)
# 构建模型函数
def model(w, x):return w * x
# 绘制直线
def draw_line(w):point_x = np.linspace(0, 5, 100)point_y = model(w, point_x)plt.plot(point_x, point_y)
print(w)
draw_line(w)
# 绘制数据点
plt.plot(x, y,'o')
plt.show()结果展示:

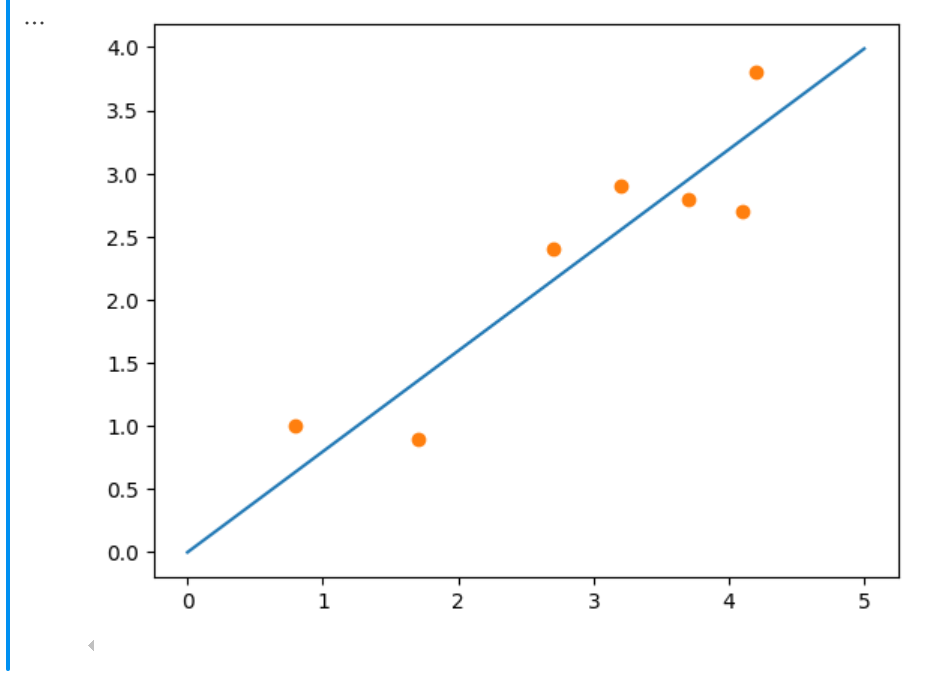
(2)两个 w (特征)的梯度下降
代码示例:
# 定义损失函数
def loss(w1, w2):return (12 * w1 + 13 * w2 - 209)**2
# 两个梯度函数,因为有两个权重w,所以分别对权重求偏导数
# 定义梯度函数
def g_w1(w1, w2):return 2 * (12 * w1 + 13 * w2 - 209) * 12
# 定义梯度函数
def g_w2(w1, w2):return 2 * (12 * w1 + 13 * w2 - 209) * 13
# 初始化w1, w2(为了举例随意选取的值)
w1 = 10
w2 = 12
# 打印当前w1, w2的模型预测的误差(均方差MSE)
print("loss(w1,w2):",loss(w1, w2))
# 使用循环实现梯度下降
for i in range(10):w1, w2 = w1 - 0.0001 * g_w1(w1, w2), w2 - 0.0001 * g_w2(w1, w2)print("w1:",w1,"w2:", w2)结果展示:
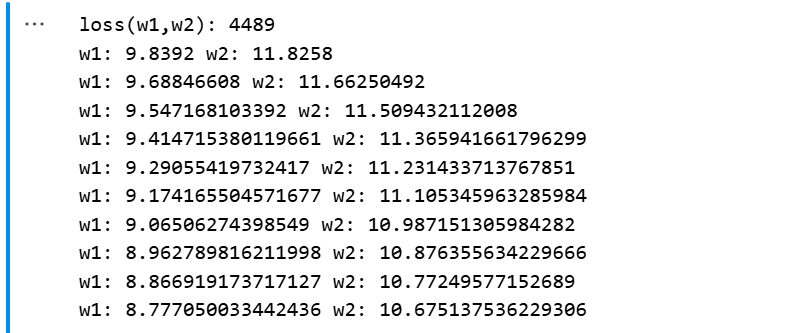
2、随机梯度下降
sklearn库有专门的SGD随机梯度下降API,直接使用即可
代码示例:
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor
import numpy as np
from sklearn.metrics import mean_squared_error # 加载数据集
x, y = fetch_california_housing(return_X_y=True, data_home="../src")
print("x.shape:", x.shape)
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=22)
# 标准化
scaler = StandardScaler()
scaler.fit(x_train)
x_train = scaler.transform(x_train)
# 创建模型 SGDRegressor(loss="squared_error") 损失函数, fit_intercept=True 是否计算截距项 max_iter 最大迭代次数 shuffle 是否打乱数据
model = SGDRegressor(loss = "squared_error", learning_rate="constant", eta0=0.0001, fit_intercept=True, max_iter=100000, shuffle = True)
# 训练
# 1.初始化w 2.构建损失函数 计算导函数 3、计算当前梯度 4、更新w,w的公式
model.fit(x_train, y_train)
# 打印权重和偏置
print("w:", model.coef_)
print("b:", model.intercept_)
# 评估
x_test = scaler.transform(x_test)
y_hat = model.predict(x_test)
loss = mean_squared_error(y_hat, y_test)
print("损失为:", loss)结果展示

3、小批量梯度下降
sklearn中并没有直接的MBGD小批量梯度下降的API,但是我们可以通过循环SGD的方法来实现我们的MBGD。
代码示例:
from sklearn.linear_model import SGDRegressor
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
import numpy as np
import math
# 加载数据集
x, y = fetch_california_housing(return_X_y=True, data_home="../src")
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=22)
# 标准化
scaler = StandardScaler()
scaler.fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)
# 模型(构建模型,预测得到预测结果(前向传播)和y_test 做损失函数 求当前w的梯度 梯度下降)
model = SGDRegressor(loss = "squared_error", learning_rate="constant", eta0=0.0001, fit_intercept=True, max_iter=100000, shuffle = True)
# 设置迭代轮数
epochs = 10
# 设置一个小批量的大小
batch_size = 32
# 总数据集的样本数
size = len(x_train)
# 计算批量数量
batch = math.ceil(size/batch_size)
# 获取索引
indexs = np.arange(size)
# shuffle() 函数打乱索引,制造随机效果
np.random.shuffle(indexs)
for epoch in range(epochs):for i in range(batch):index = indexs[batch_size*i:min(batch_size*(i+1),size)]x = x_train[index]y = y_train[index]# 使用partial_fit() 方法训练,训练后保存相关参数,确保下一次训练时,使用上一次的参数model.partial_fit(x, y)print(f"epoch/epochs:,{epoch+1}/{epochs} loss: {np.mean((model.predict(x_test) - y_test)**2)}")model.partial_fit(x_train, y_train)
# 打印权重weight 和偏置 bias
print("w:", model.coef_)
print("b:", model.intercept_)结果展示:
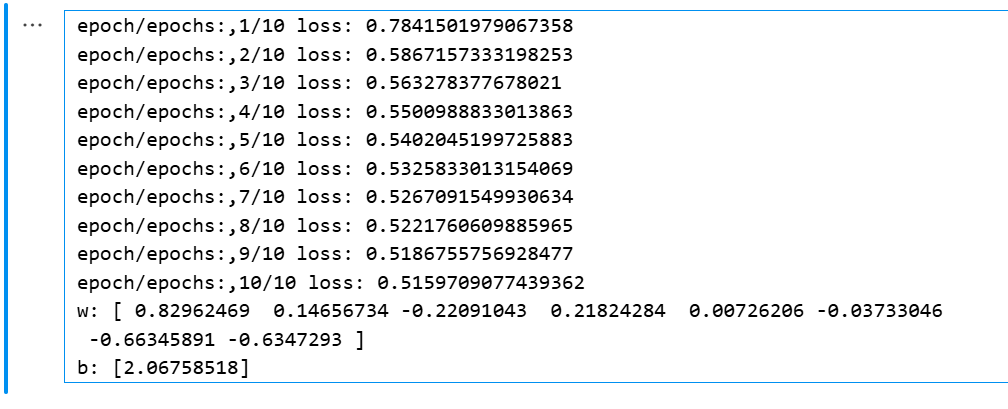
四、总结
梯度下降思想是我们在接下来的机器学习领域(包括深度学习等)都十分重要的一个思想,我们要掌握其不断“猜”并且根据误差不断调整的思路和方法。可以试着自己手动实现一个小批量梯度下降的小项目!
希望这篇博客对你有所帮助!如果有任何问题,欢迎进一步讨论。
