考研复习-计算机组成原理-第三章-存储系统
本文章只记录书中未有的内容,仅供本人学习
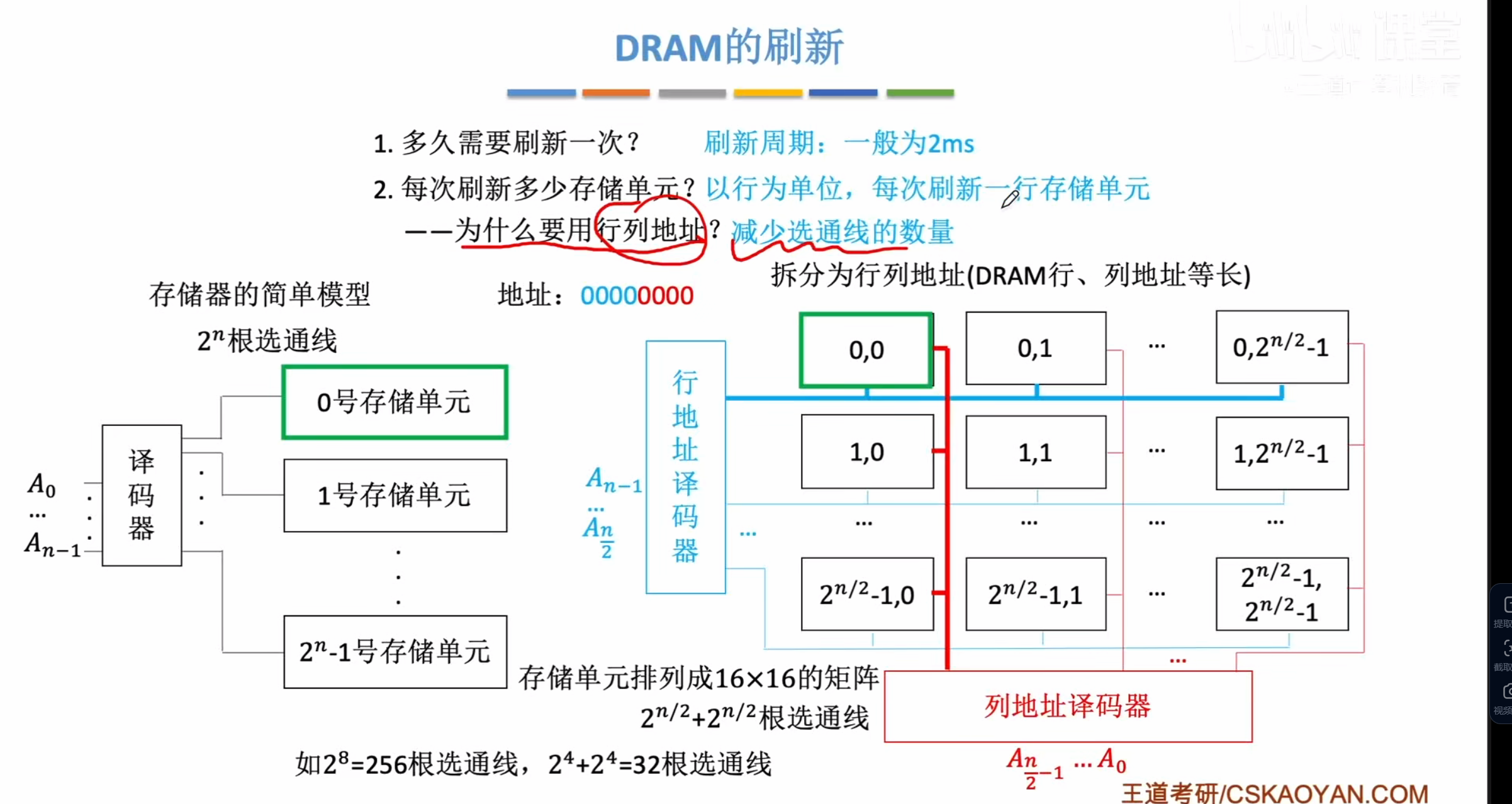
DRAM
结构
采用行列地址排布
即原本的一维线性排布变成行列二维排布
假定一共有=256个存储元
线性排布需要256个选通线
但是对于DRAM来说我们采用二维存储
即=
=16根行地址线
总线数就是32根线
将八位地址码分为前后两部分,当前四位选通某行,后四位选通某列,只有当行列都选通某个值的时候才会选择到某个单元
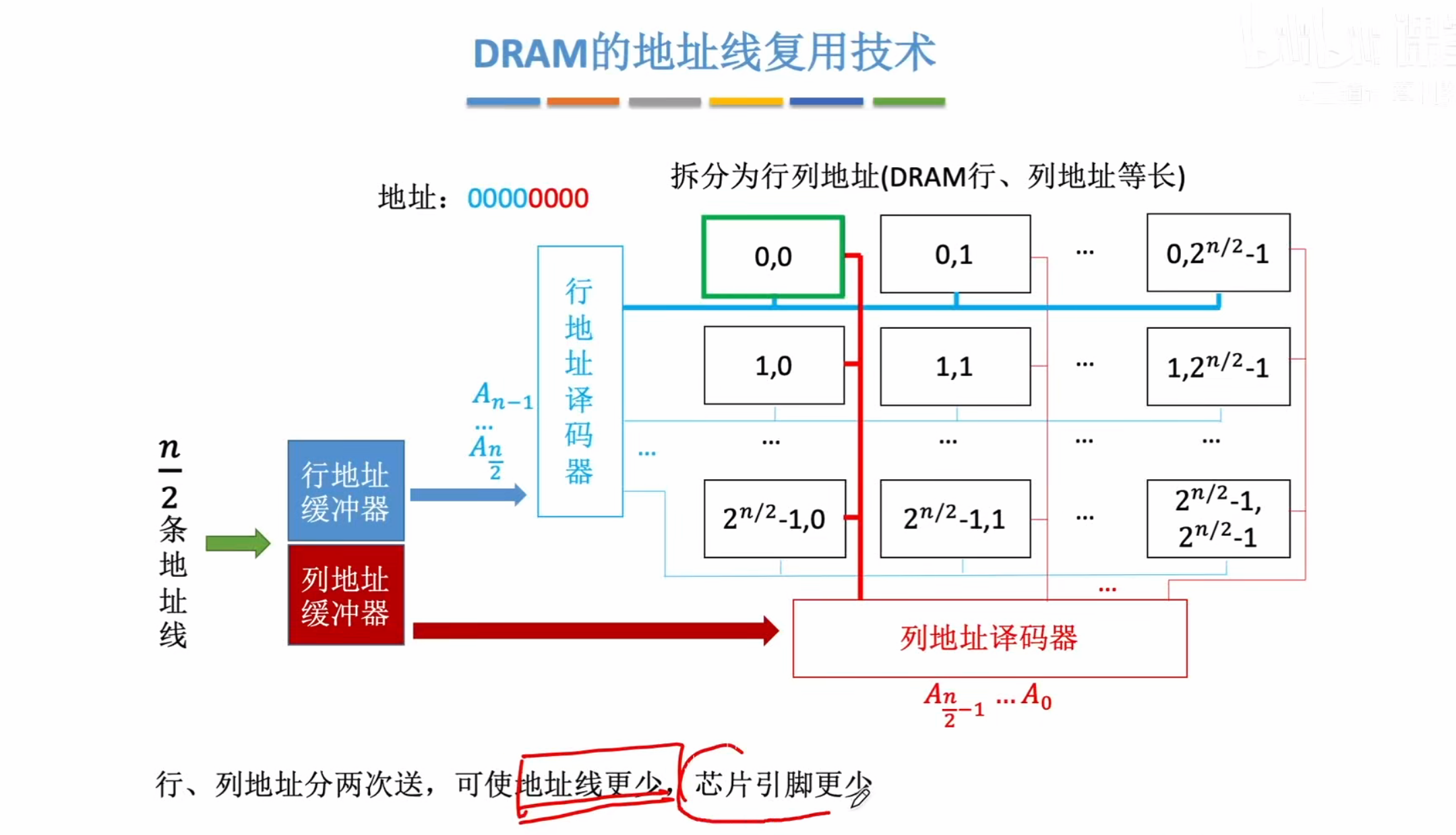
地址线复用技术
刷新相关知识补充
好的,我们来详细拆解一下DRAM刷新的“死区”以及不同刷新方式的差异。
首先,我们需要理解DRAM(动态随机存取存储器)的工作原理。DRAM的每个存储单元由一个小电容和一个晶体管组成,通过电容的充电状态来表示0和1。然而,电容会随着时间的推移而漏电,如果不进行处理,存储的数据就会丢失。因此,必须定期对DRAM进行“刷新”(Refresh)操作,即重新读取数据并写回,以恢复电荷。
什么是DRAM刷新的“死区”?
DRAM刷新的“死区”(Dead Time)指的是因进行刷新操作而导致CPU无法访问存储器的时间段。在“死区”期间,内存控制器正忙于刷新某一行或多行存储单元,无法响应CPU的读/写请求,CPU只能等待,这会造成系统性能的短暂下降。
为什么异步刷新有“死区”?
异步刷新(Asynchronous Refresh)是一种将刷新操作分散到整个刷新周期内执行的方式。它并非完全没有“死区”,而是将一个大的、集中的“死区”分解成了许多个微小的、分散的“死区”。
其工作流程如下:
分时刷新:假设DRAM要求在2ms内刷新完所有行(例如128行)。异步刷新会计算出每隔一小段时间(例如 2ms / 128 = 15.6μs)就必须刷新一行。[1][2]
微小死区:在这15.6μs的时间段内,大部分时间CPU可以自由访问内存。但是,当刷新操作真正执行时(例如需要0.5μs来刷新一行),在这0.5μs的时间里,被刷新的那一行所在的存储体(Bank)是无法被访问的。[2][3] 这就是异步刷新的“死区”。
流程特点:其流程更像是“(多次)读/写...(一次短暂的)刷新...(多次)读/写...(一次短暂的)刷新...”。虽然刷新操作插入到了正常的读/写流程之间,但它仍然是一个独立且占用内存总线的操作,会短暂地阻塞CPU的访问请求。
可以把异步刷新想象成银行办理业务。银行正常对外营业(CPU可访问内存),但每隔15分钟,其中一个窗口就要暂停服务1分钟进行内部盘点(刷新一行)。对于需要使用这个窗口的客户(需要访问该存储体的CPU)来说,这1分钟就是“死区”。
为什么分散刷新没有“死区”?
分散刷新(Distributed Refresh)从根本上改变了操作流程,从而消除了传统意义上的“死区”。
其工作流程如下:
绑定操作:分散刷新将刷新操作与每一次读/写操作绑定在一起。[2][3] 它将一个完整的存取周期(例如1μs)一分为二。
两段式周期:前半段(例如0.5μs)用于执行CPU的正常读/写操作,后半段(例如0.5μs)则固定用于刷新DRAM的某一行。[2][4]
流程特点:因此,它的流程是严格的“读-刷新,写-刷新,读-刷新...”。CPU每次访问内存,都必然伴随着一次刷新操作。由于刷新操作被整合进了每个存取周期内部,系统不再需要专门中断读/写来执行刷新,因此也就没有了CPU无法访问内存的“死区”。[4][5]
同样用银行的例子来比喻,分散刷新相当于银行改变了服务流程。现在,每个窗口办理任何一笔业务(读/写)后,都必须强制花30秒进行一次内部账目核对(刷新)。虽然客户办理业务的总时长变长了,但银行从未“暂停服务”,对于客户来说,银行总是在“可访问”状态,没有出现关门谢客的“死区”。
总结与对比
特性 异步刷新 (Asynchronous Refresh) 分散刷新 (Distributed Refresh) 刷新时机 在固定的时间间隔(如15.6μs)内插入一次行刷新操作。 每次读/写操作都捆绑一次行刷新操作。[3] 死区 有,存在微小、间歇性的死区。在刷新某一行时,该行所在的Bank无法响应CPU请求。[5] 无,不存在CPU无法访问内存的死区时间。[4] 存取周期 存取周期基本不变,系统整体速度受影响较小。 每个存取周期都被延长(例如增加一倍),导致系统整体速度显著下降。[2][5] 刷新效率 刷新操作的频率恰好满足DRAM的要求,不多也不少,效率较高。 刷新操作非常频繁,远超DRAM的最低要求,会造成不必要的性能损耗和硬件磨损。[2][4] 流程 读/写...读/写...刷新...读/写... 读-刷新...写-刷新...读-刷新... 总的来说,异步刷新是通过将一个大的死区分解成多个不易察觉的小死区来提高系统效率,是一种在性能和刷新需求之间的折中方案。[5] 而分散刷新则是通过延长每一个操作时间来彻底消除“死区”,但代价是系统整体性能的降低。[4] 正是这两种不同的处理逻辑,决定了它们在“死区”问题上表现的差异。
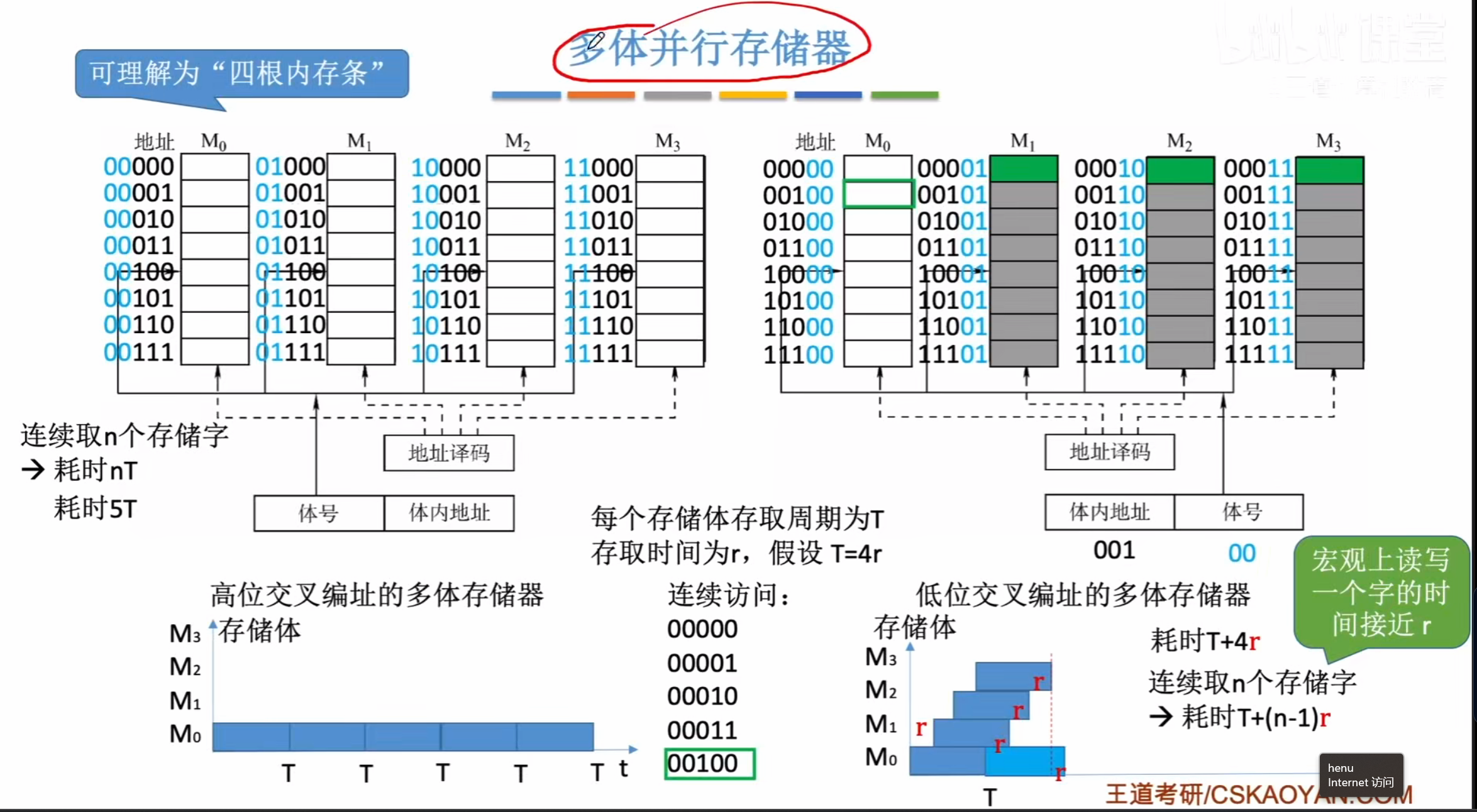
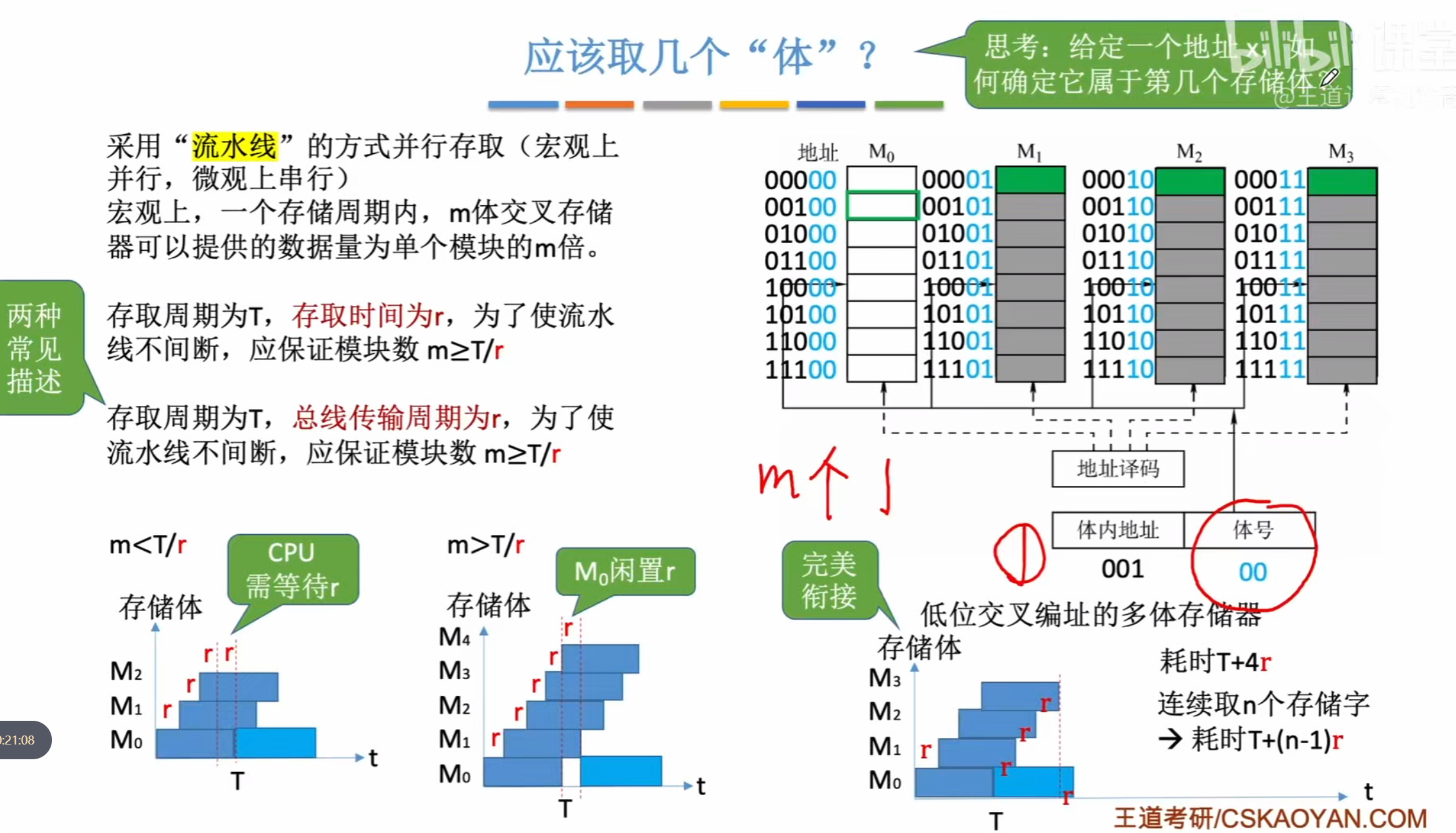
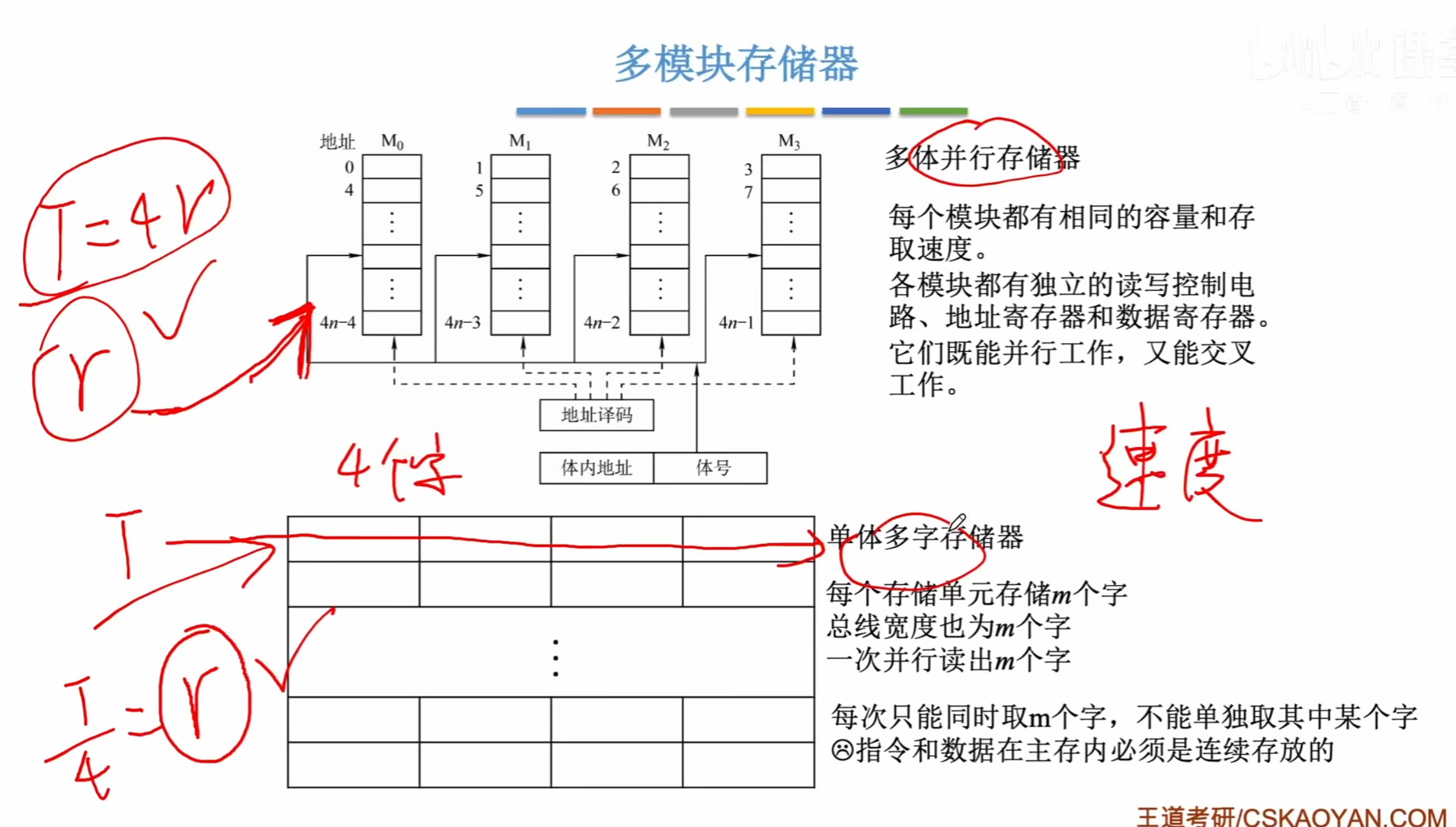
多体并行存储器
高低位交叉编址的差别

假定读取如图所示的四个连续的存储单元
采用高位编址则因为这几个存储元都在一个存储器中
所以不能够连续的进行读取,而是要等一个存储周期完全恢复才可以进行下一次读取
导致耗时很长
而对于低位交叉编址能够访问不同的存储器,所以能够同时读取,每次读取耗费1r时间
总的来说读取n个存储字需要耗费如图所示的时间
r代表的是读取一个字的时间,读取n个字实际时间只需要一个周期,只不过后面的(n-1)r是用于给存储体进行回复的时间
低位交叉编制的存储体的最小数量
如图所示,若模块数小于
则会发生当所有的存储体都读取完了一遍之后,再次读取需要等待存储体的回复
而若m>
则会有一个芯片回复过后空余出来了闲置时间
所以m=是最好的
与单体多字的对比
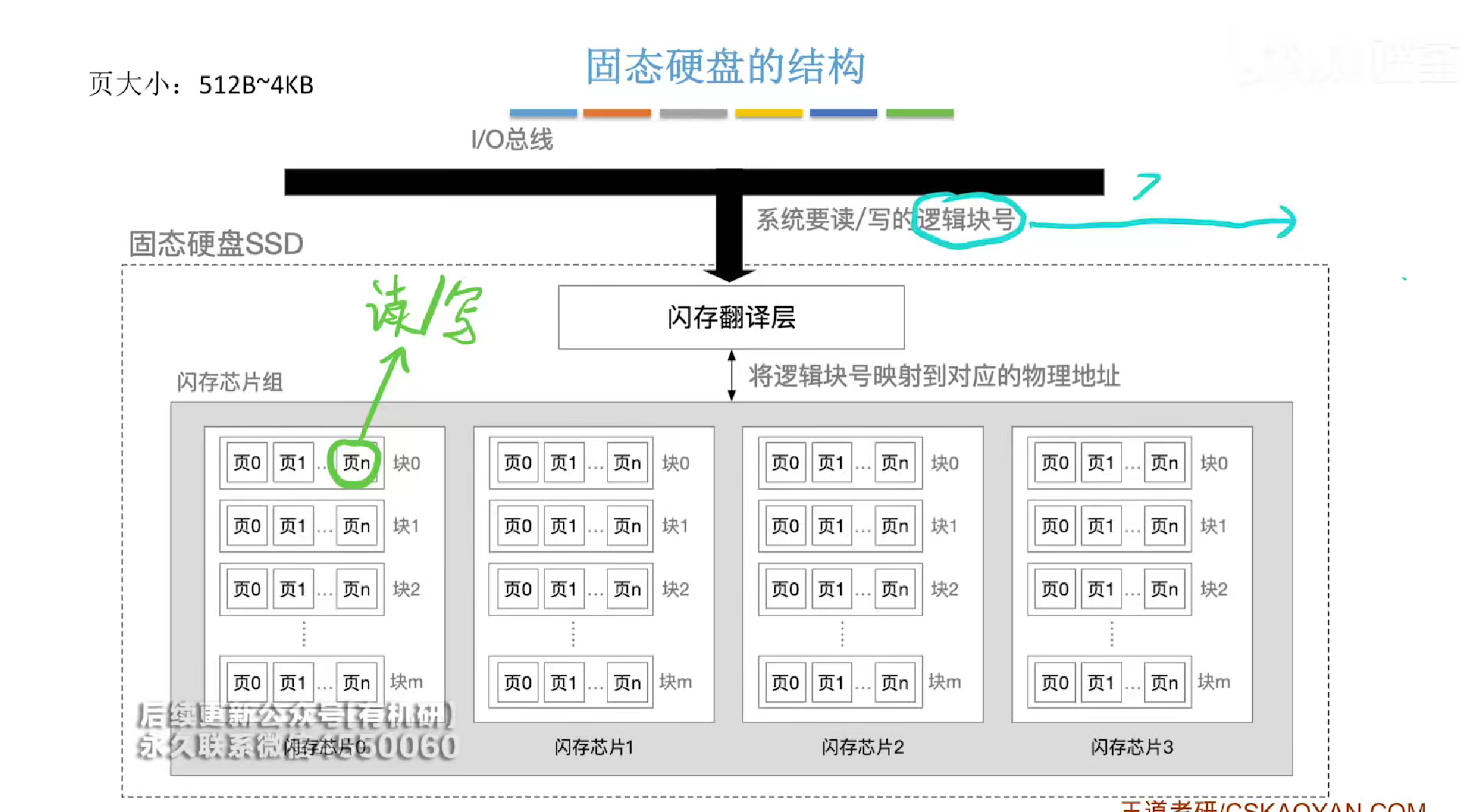
SSD固态硬盘
结构如下
一个ssd有多个芯片,每个芯片有多个块,每个块有多个页,而每一次读写都是以页为单位
固态硬盘的一个页相当于磁盘的一个扇区
一个块相当于一个磁道
闪存翻译成一个对应的页号
以块为单位进行擦除
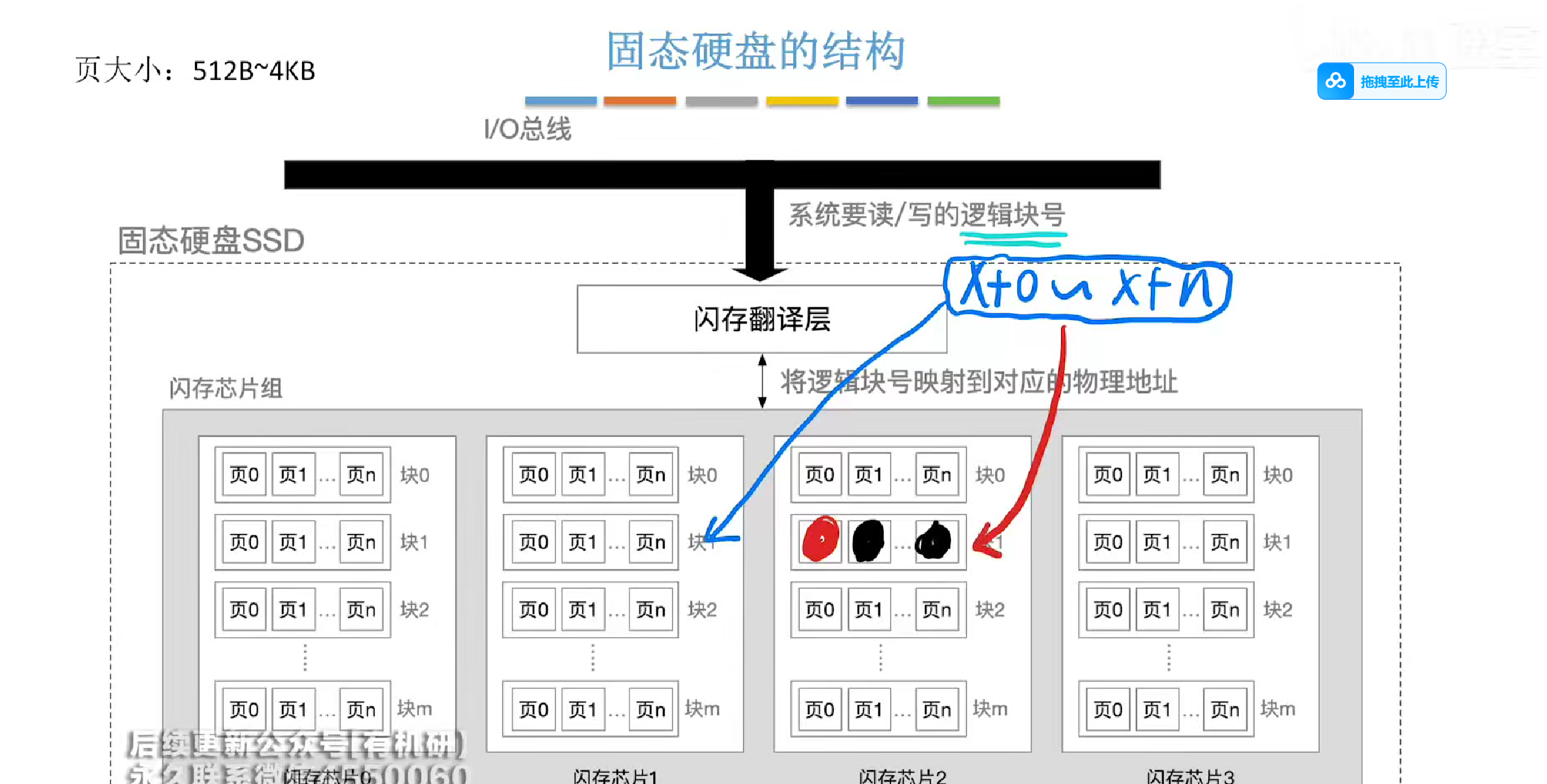
而在以块为单位进行擦除的时候
有时候我们可能只是想擦除一个页,但是会导致整个块被擦除
我们在擦除前会把里面的内容全部映射到一个新的块中
然后再重新映射一遍逻辑地址
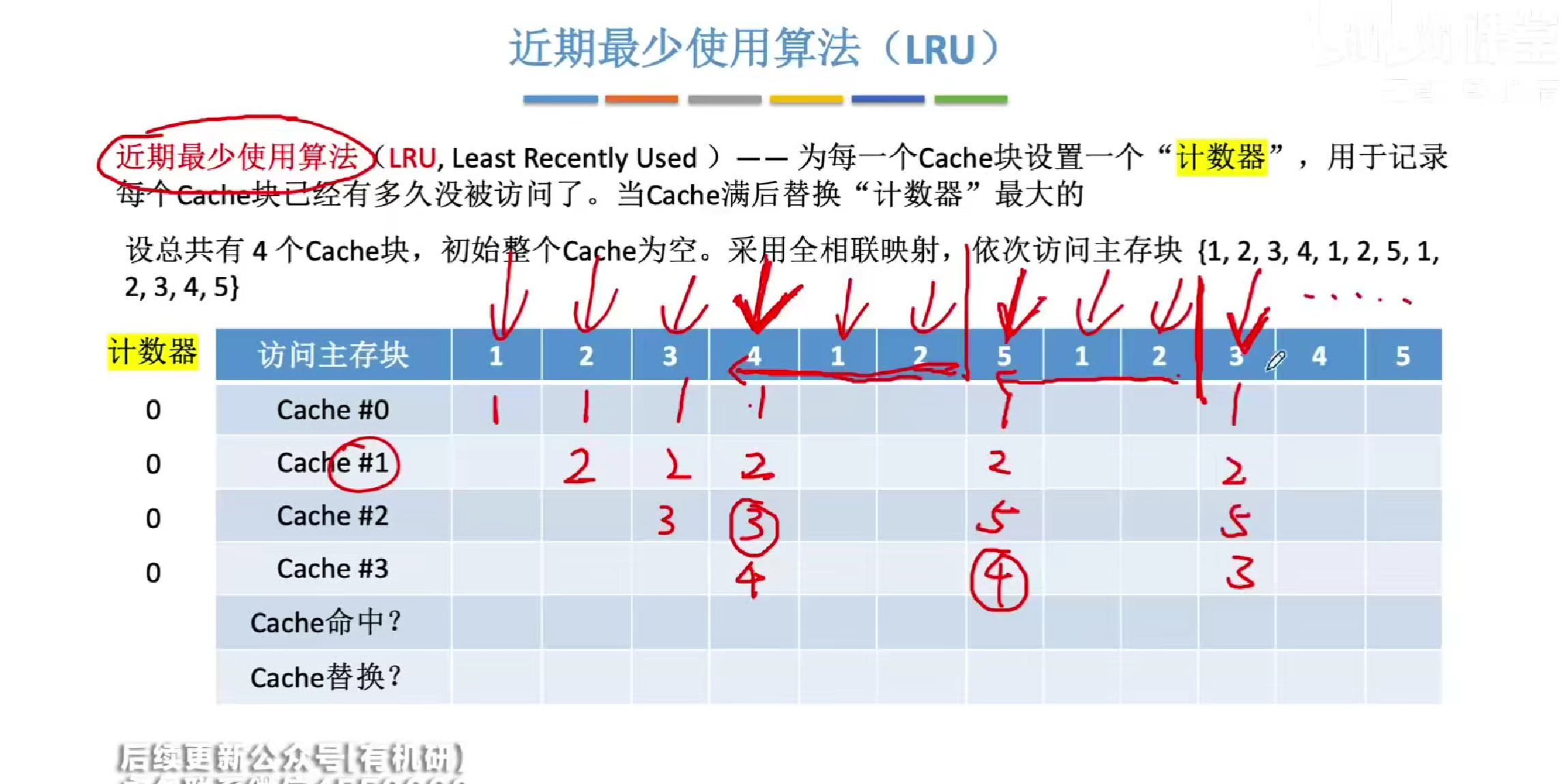
LRU算法的做题解法
如若遇见冲突则往前寻找三个不同的元素,其中没有被访问的直接换出,不需要那么麻烦手算
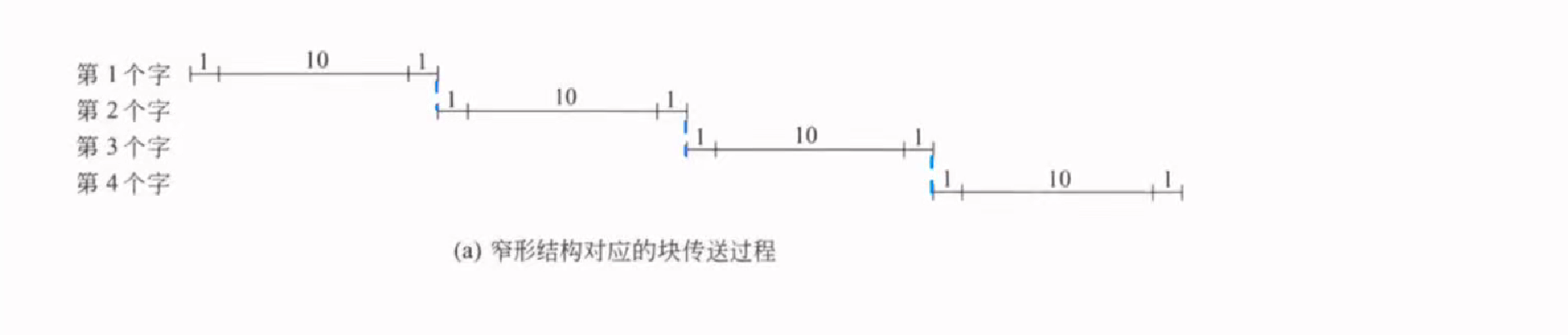
cache传送模式补充

其中传送的结构为
[发送指令,准备数据,发送数据]
这样的三个阶段
窄型结构
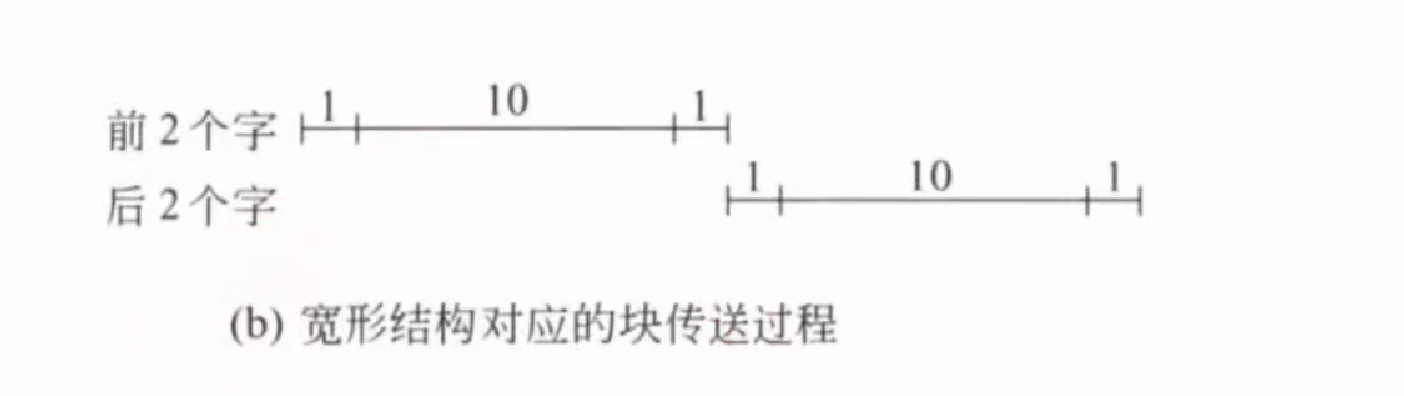
宽型结构
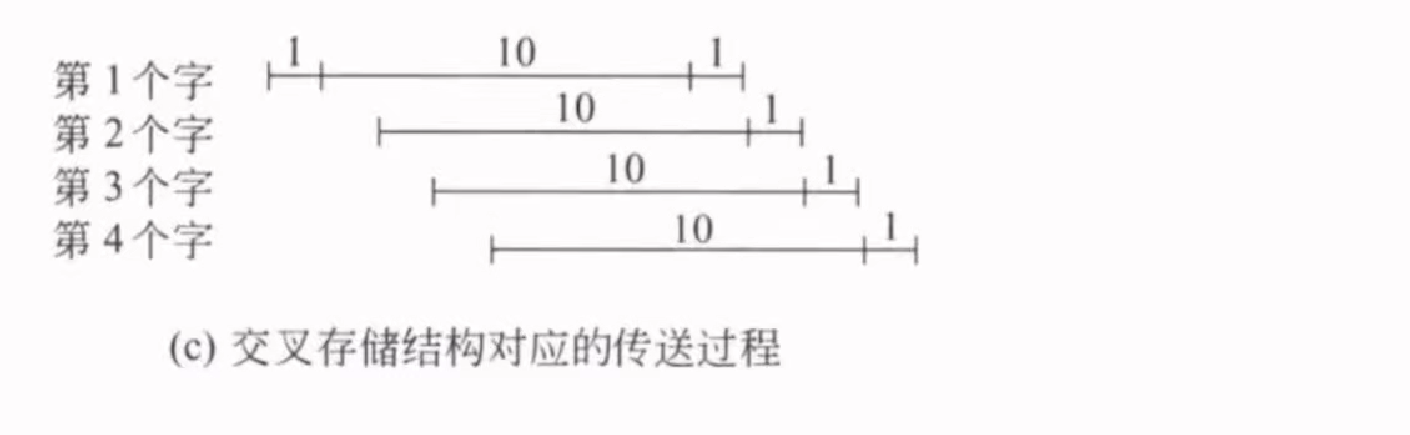
交叉存储结构
错题
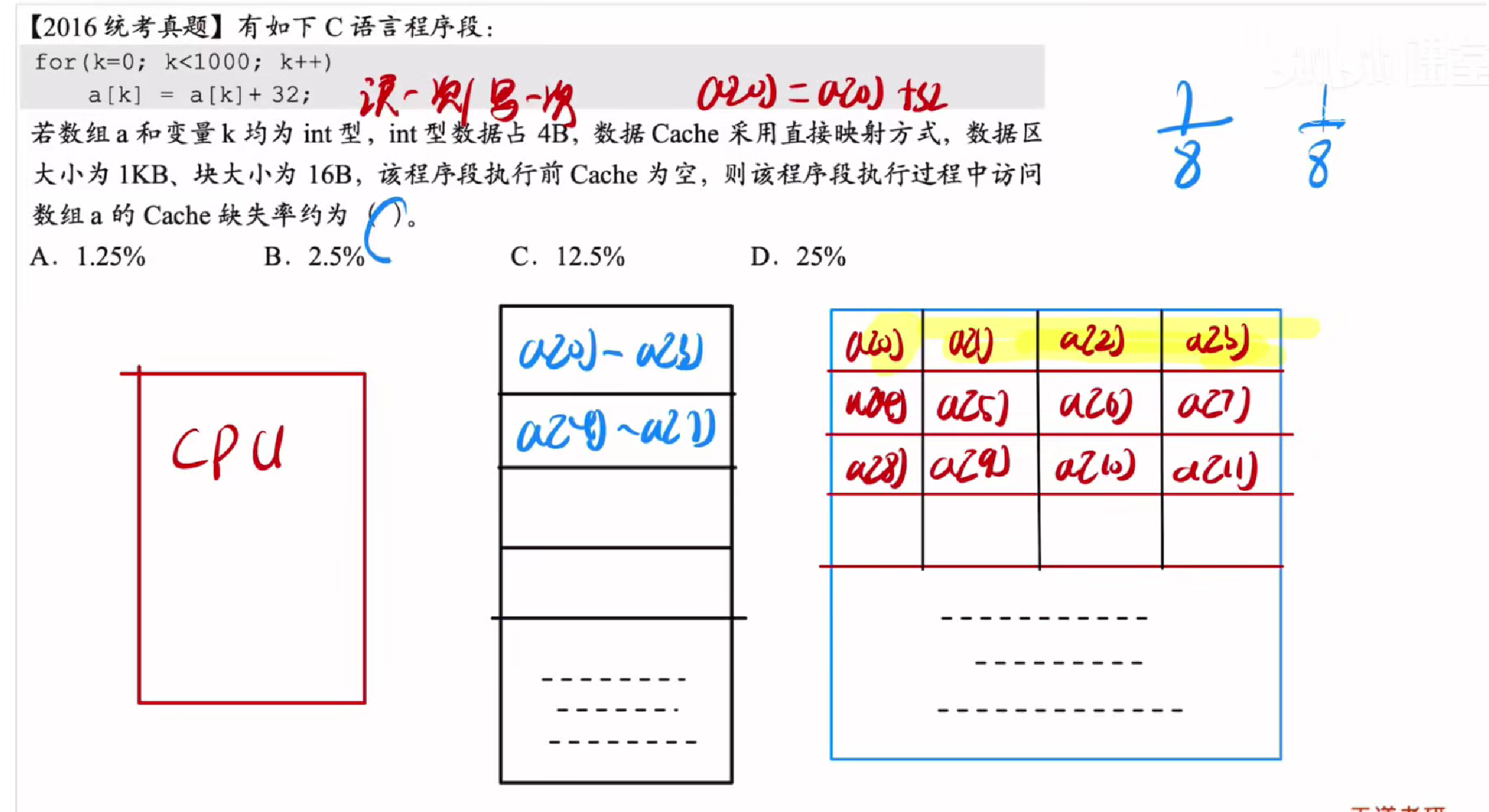
答案:C
主要是明白cache的工作原理
cache当没有命中时会从主存中调入一块元素
如图所示的一块有四个数组元素
那么我们每一块元素除了第一块元素的第一次访问不会命中,其他的都会命中
而一次代码执行的过程中
对于每一个元素都会访问两次
x=x+32
第一次访问x读取x的原本数值
第二次则是写回x的新数值,而除了每一组的第一个元素的读操作不会被命中,其他操作均会明宏
一组4个元素,一个元素访问两次,总共访问为8次,8次命中7次
所以缺失率为12.5%
答案:B
先进先出算法需要记录哪个数据先进来
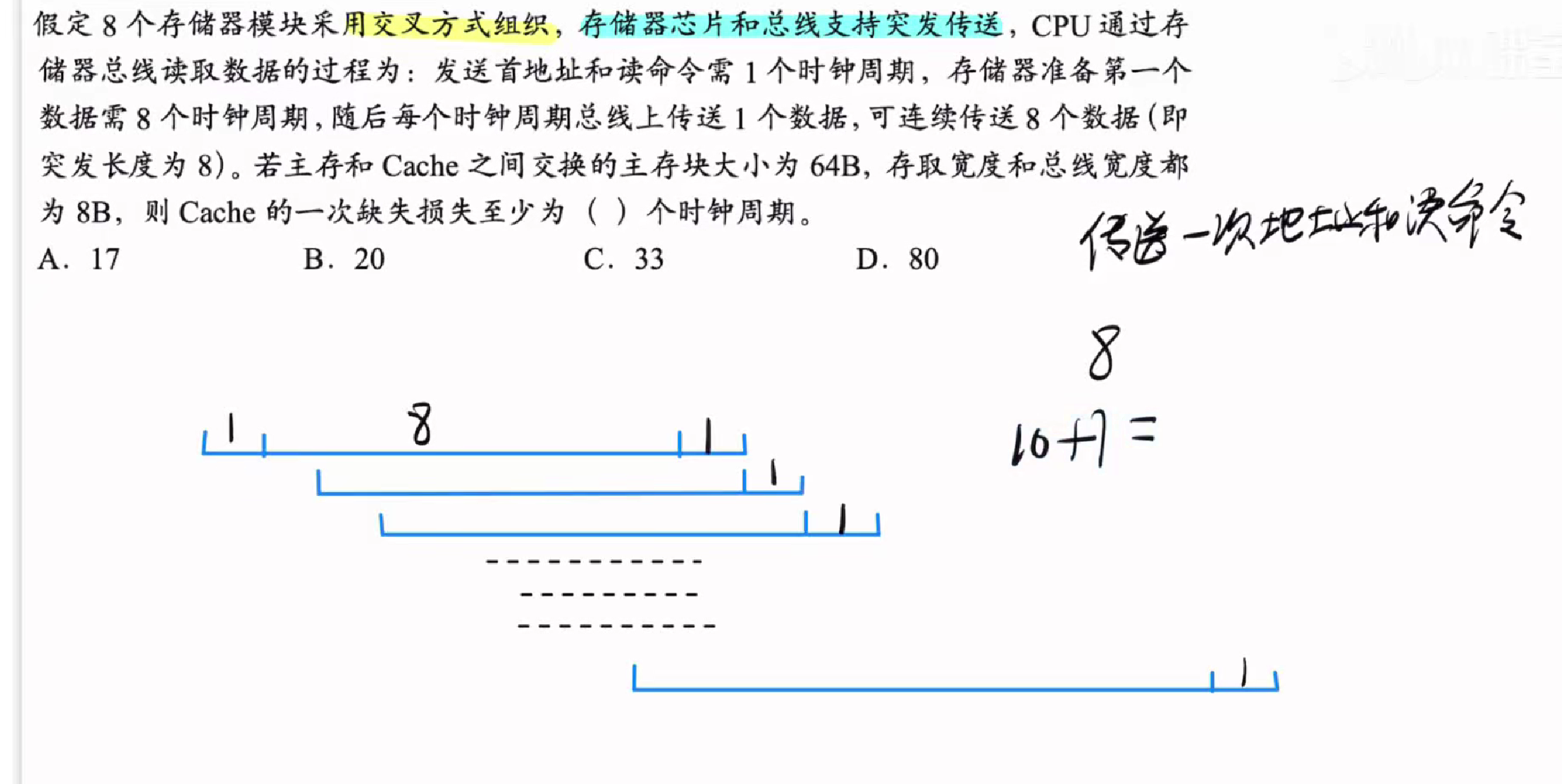
答案:A
如图所示,多模块交叉存储的时间如下所示
突发传送的含义是一次命令能够传送多个数据
如下所示,省去了命令发送的时钟周期
我们发现当第一次数据完整的传输完毕后
每隔一个时钟周期就会再发送一组数据
总共八组
所以总时间为10+7=17
重要错题该题
我们首先要明白cache的结构
[标记,数据]注意,这里的易错点在于cache和主存的结构不同,这里是直接的数据而非什么块内地址,块内地址什么的机器已经帮忙分好了
所以我们发现该题计算方式如下
数据位为题目所给32位,tag位为32-2(主存的块内地址位数)=30
加上两个判别位数
一个cache总共有
64位
而该题总共有32k行
答案为32×64=2048k

答案:B
因为块内地址+1组号也随着-1
不影响tag

答案:C
最小单位是一个扇区
扇区如果格式化是可能存放地址信息的

如图所示公式
旋转等待时间为转版权所需时间
即60/1000*1/2
得到结果为3ms
传输速率的计算是20×
用4kb去进行计算
得到B

答案:D
对于这类题目,我们只需要用大地址减去小地址+1然后计算总共需要多少位就可以得到结果了
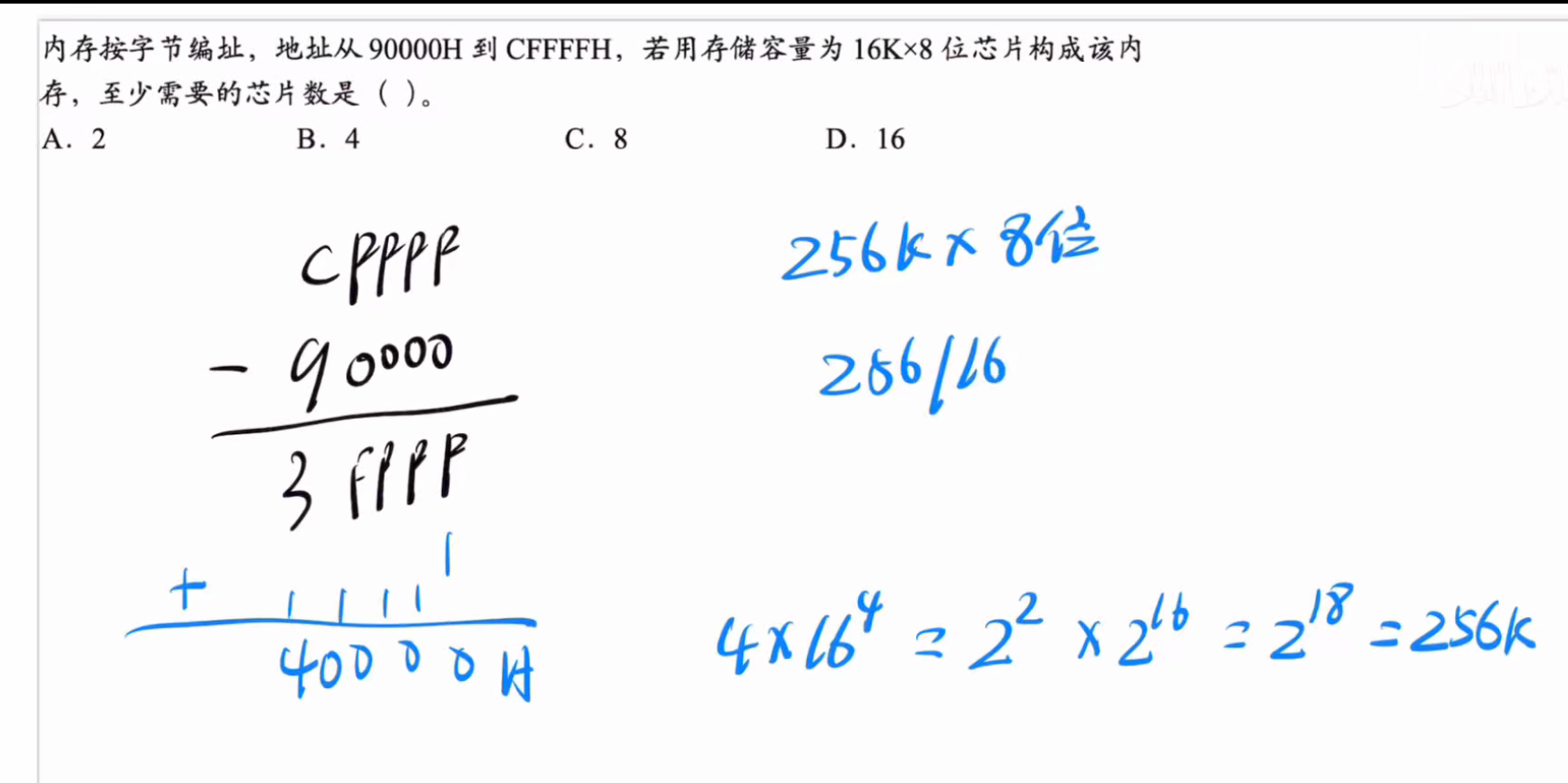
答案:C
其中主要不明白D为什么错误
其中D这样看
行缓冲指的是是将一行的数据装入缓冲中,所以等于列数×每一个单元中的位数
注意题目描述的是芯片内而不是整体
所以d正确

答案:A
对于这种多芯片组合成大芯片的,他们可以多个拼接到一起,而地址线仍然不变,只不过同样的地址线相对于之前会多选择更多的数据而已,所以只关注小的DRAM芯片构成
即
所以需要11个地址线
然后八位数据输出则需要八个数据线,所以选择a
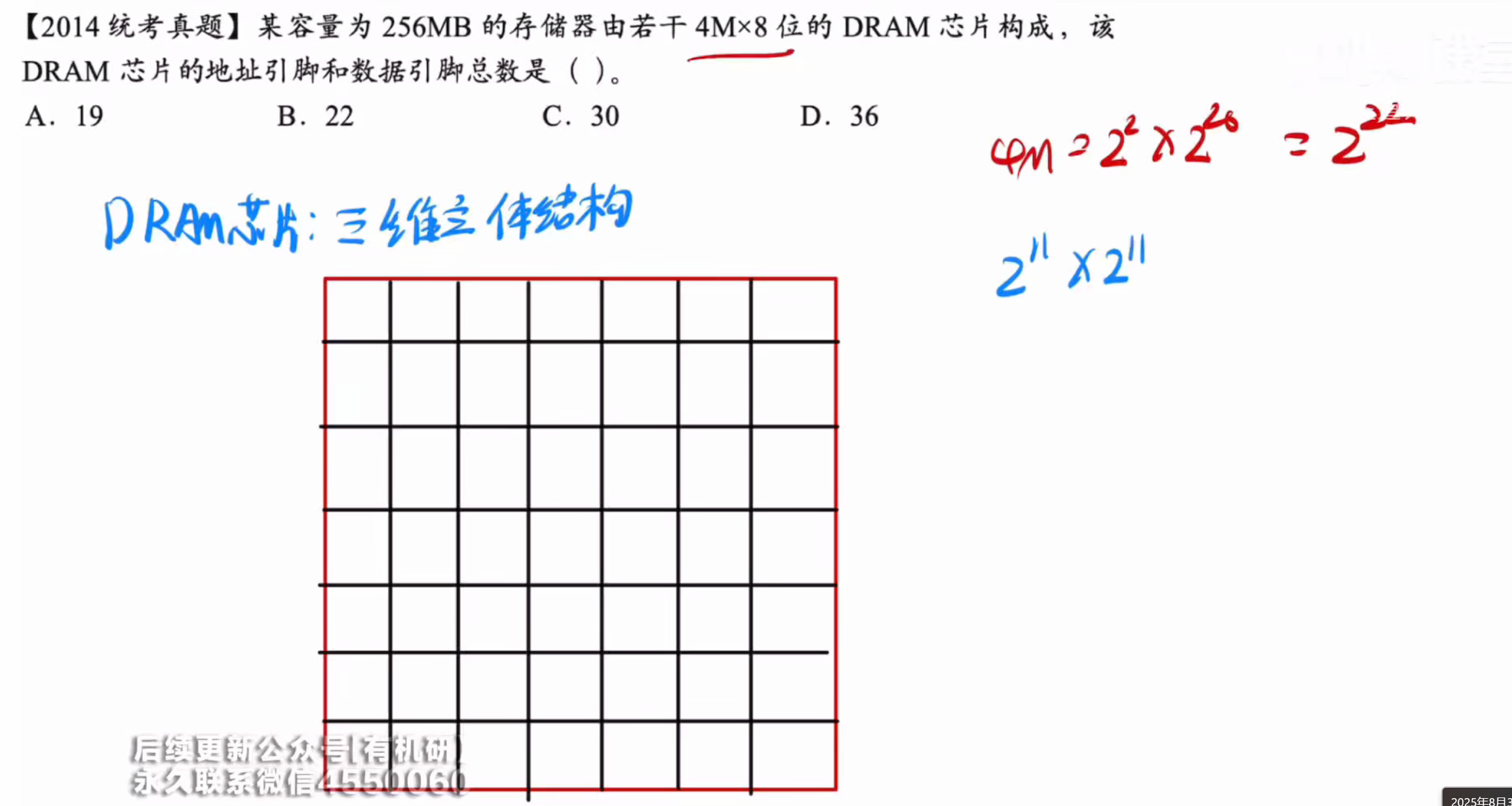
答案:A
闪存就是rom
就是flash
其写数据之前要先擦除数据所以写速度比读要慢
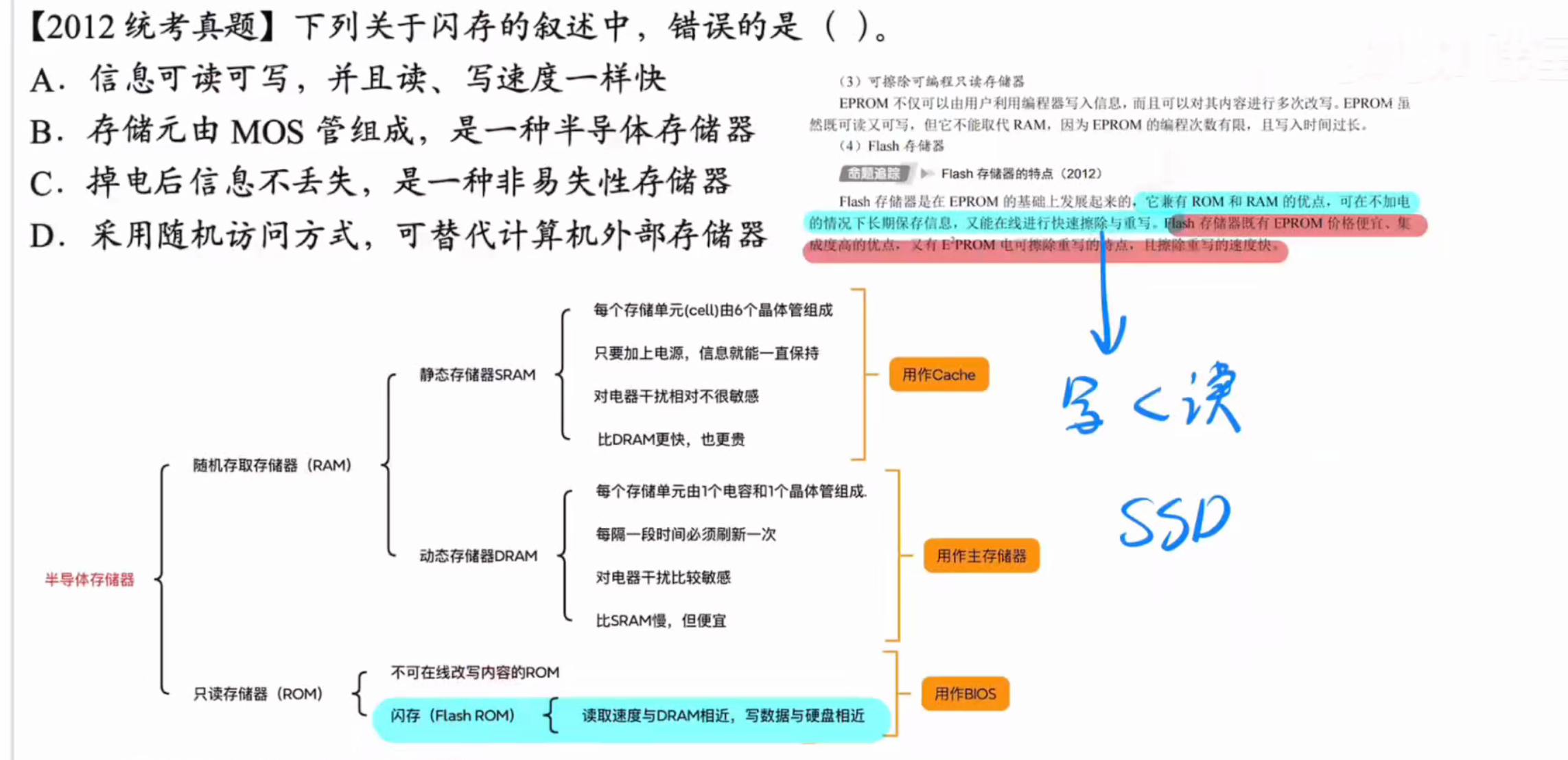
答案:A
单体多字主要在于提高存取速度

答案:D
对于该题来说,主要的点在于
交叉编址方式是什么意思
图中红线部分表明了交叉编址和连续编址分别指的是什么
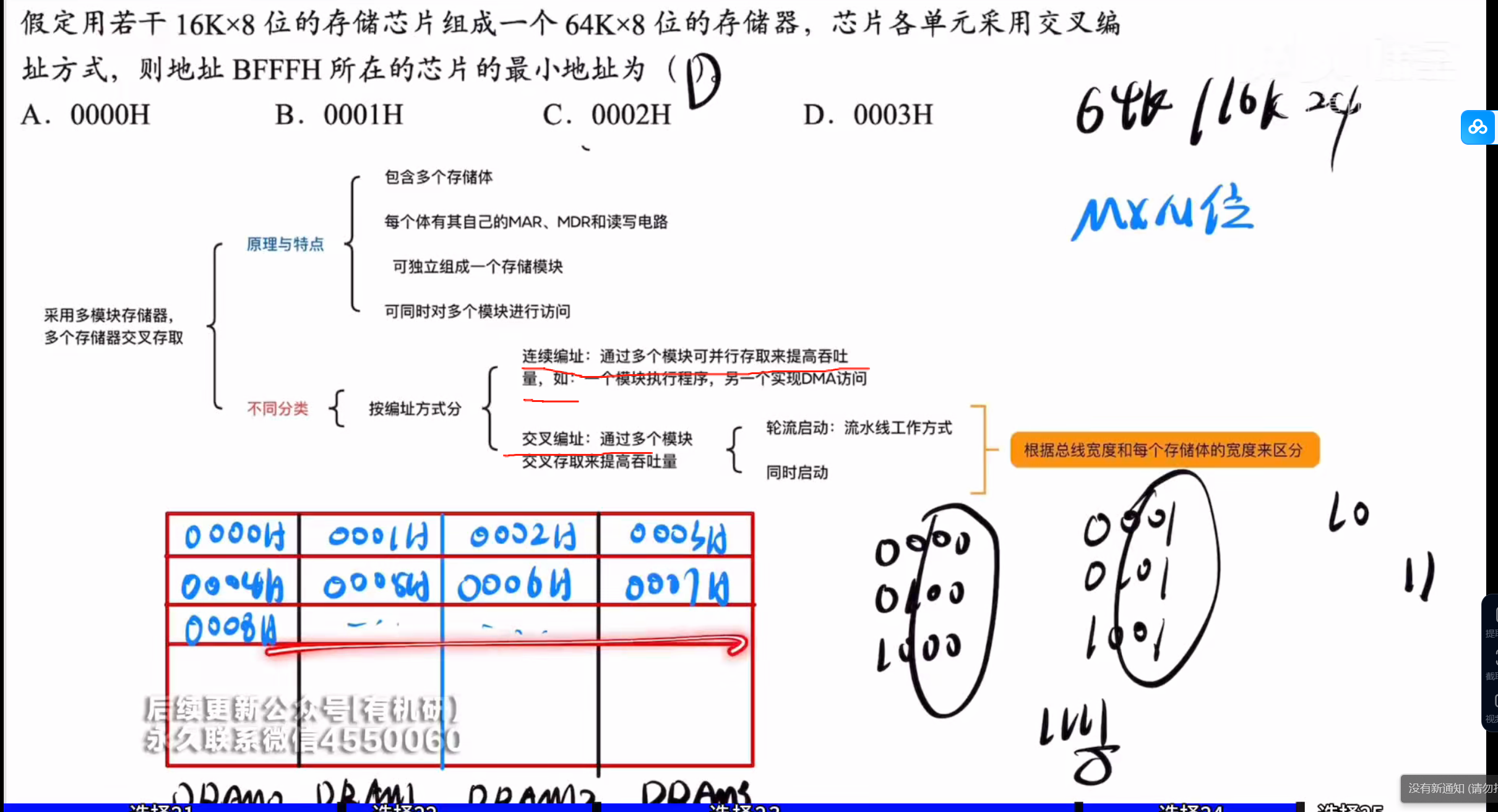
答案:C
主要是①会断流
如图所示就可发现,当读完一轮六个存储元之后,我们再次重复会发现断流现象
因为此时0号单元还在工作不能够进行读取,所以发生了断流并需要等待其工作完成才能进行下一步
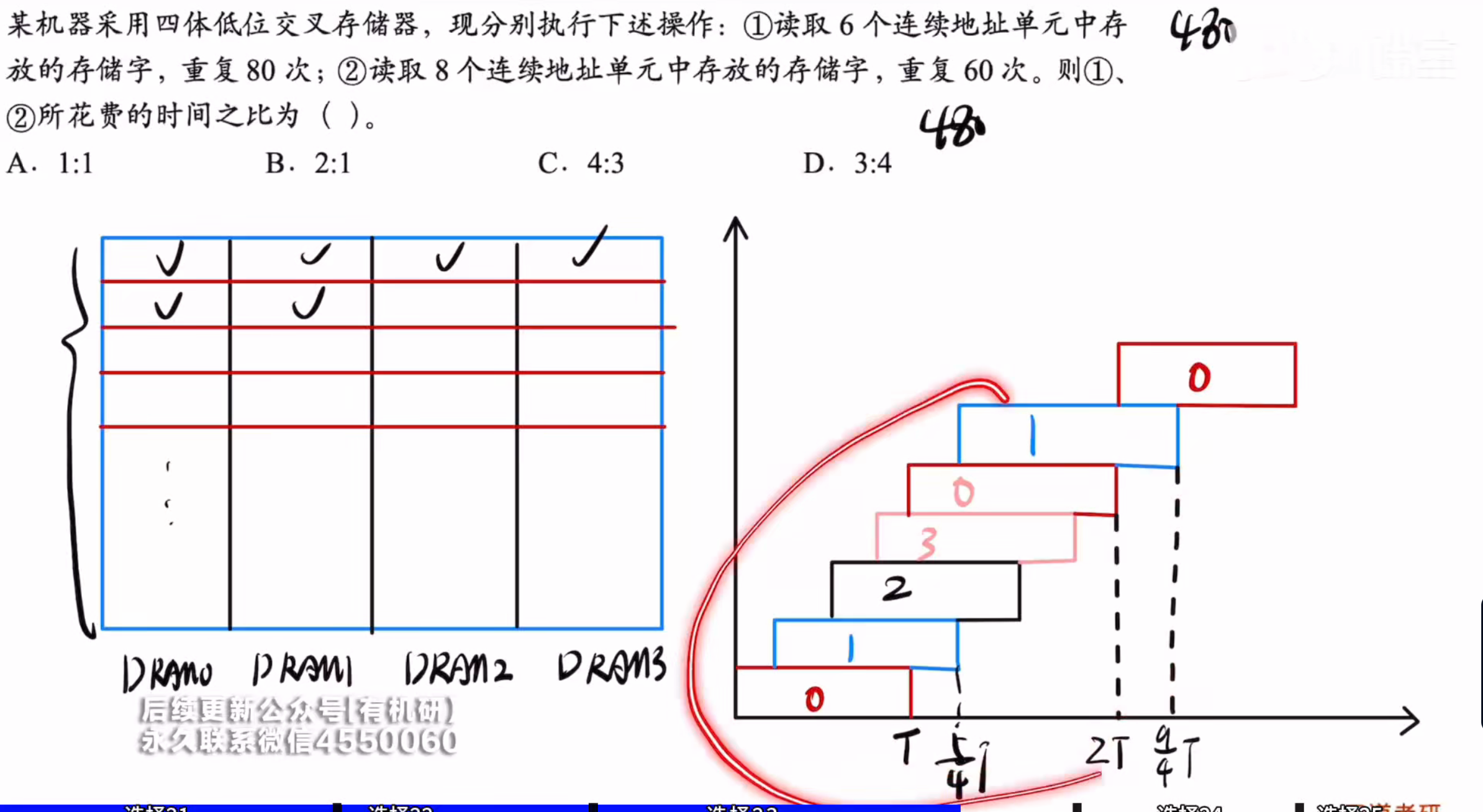
答案:B
其中位平面指的是一个存储单元有多少位
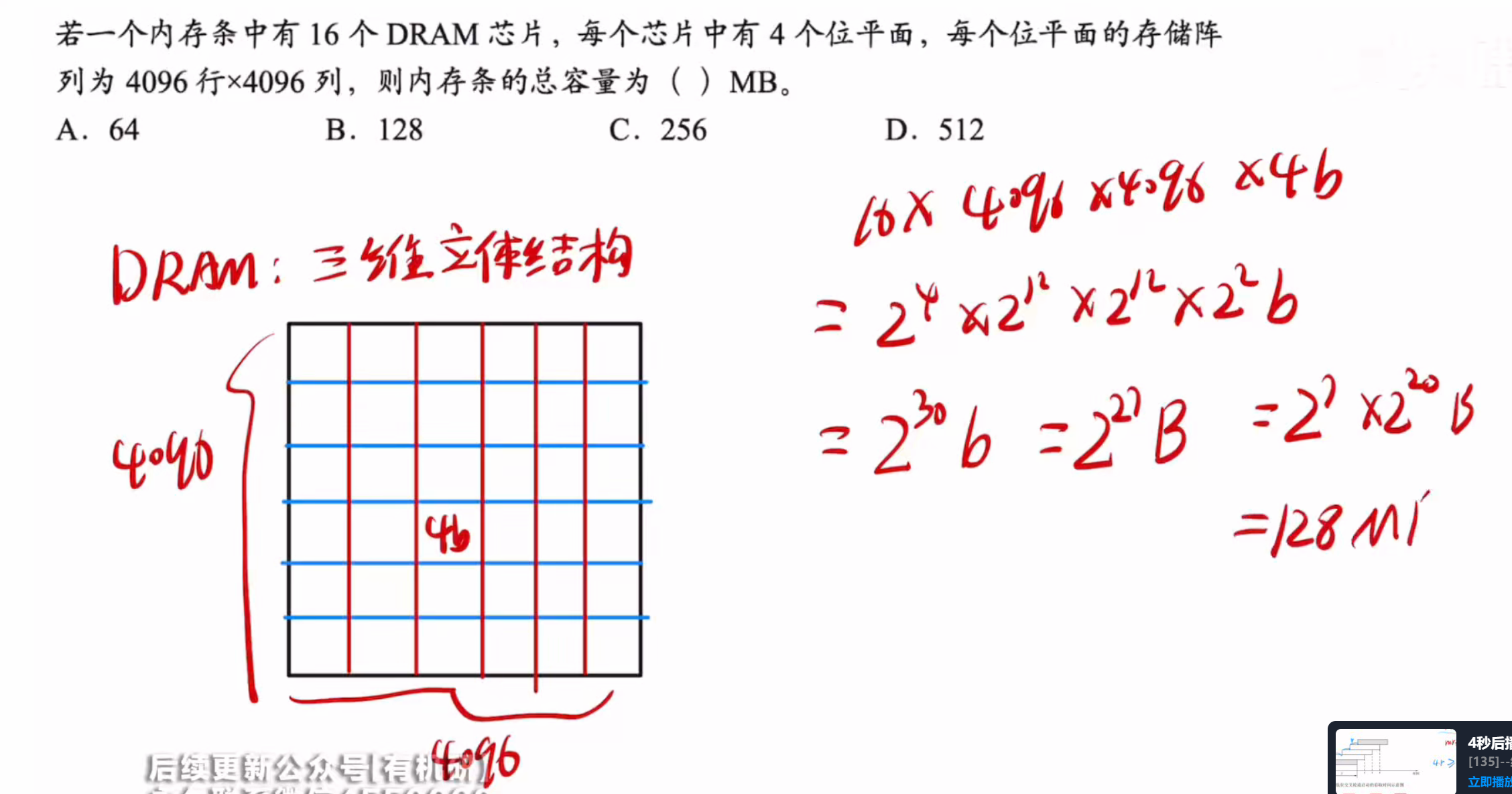
答案:B
其中,1024指的是总共有多少个存储单元
而8指的是一个存储单元有多少位数据存储
采用地址复用技术则是一个立方体形状
则地址线为5
然后数据线是负责传输8 bit位信息的,所以数据线有八个总共13个引脚
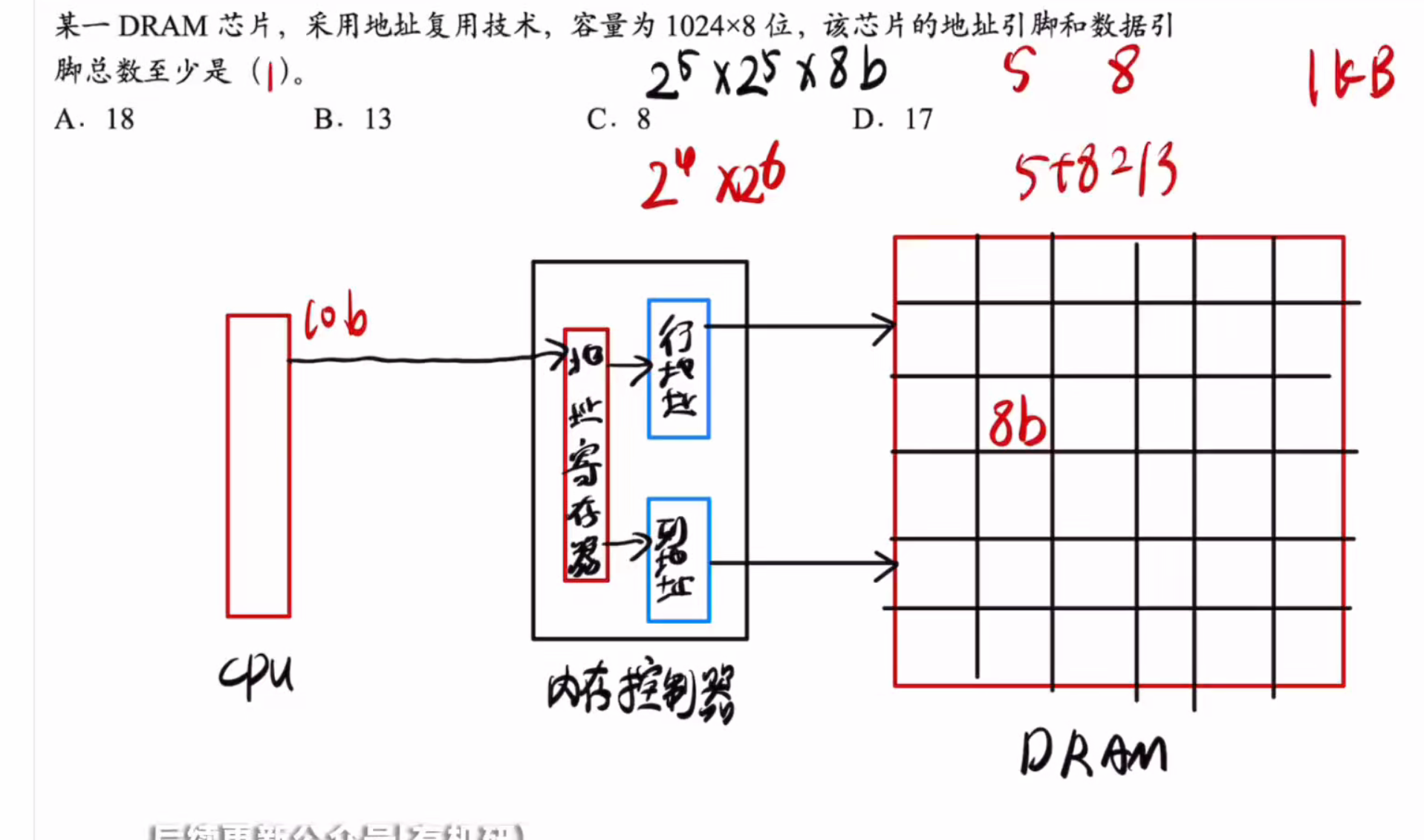
答案:A
可以统一编址
比如主存就需要rom来完成操作系统的自举程序
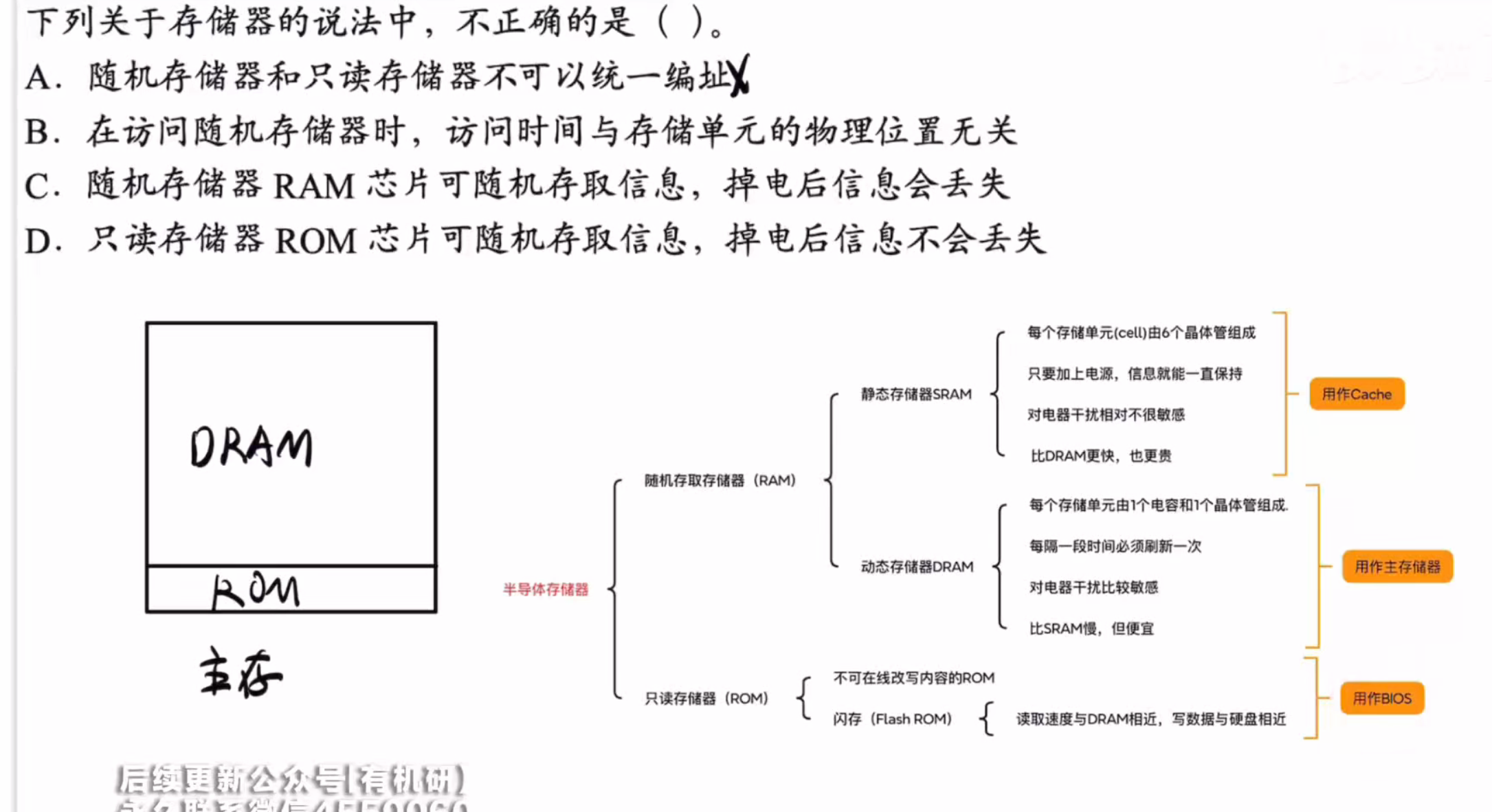
答案:D
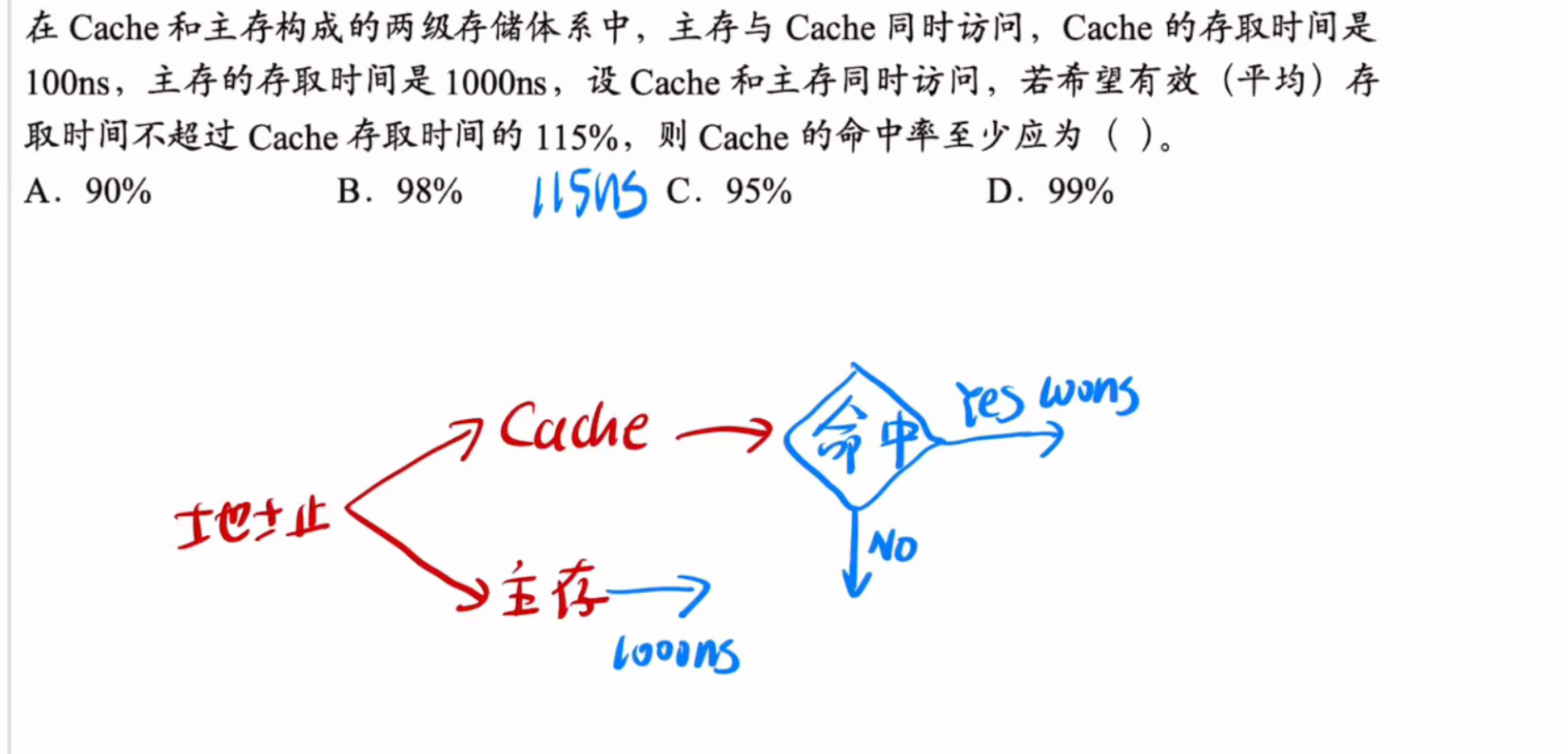
计算其数学期望,假定cache命中概率为x
则有
100ns*x+1000ns*(1-x)<=115ns
计算得到结果为d