当前位置： 首页 > news >正文

河南萌新联赛2025第（四）场：河南大学(补题）

news 2025/8/8 10:24:15

文章目录

  • A.完美序列
  • B.0！！！！！
  • C.合并石子
  • D.箭头谜题Ⅰ
  • G.封闭运算
  • J.故障机器人的完美牌组
  • L.故障机器人的完美遗物
  • 总结

A.完美序列

A.完美序列

在这里插入图片描述
当时没怎么想就直接暴力枚举一下，通过map计数来找到满足的，只是漏了一些细节，没有考虑到2 2 2 2 2这种情况
最后修改一下过了
代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll s[N];
void solve()
{ll n;cin>>n;unordered_map<ll,ll>m;for(ll i=1;i<=n;i++)cin>>s[i],m[s[i]]++;if(n<=2){if(n==1)cout<<0<<endl;elsecout<<2<<endl;return;}sort(s+1,s+n+1);ll ans=0;for(ll i=s[1]+s[2];i<=s[n]+s[n-1];i++){ll cnt=0;for(auto j:m){if(m.count(i-j.fi)&&i-j.fi!=j.fi){cnt+=min(j.se,m[i-j.fi]);}else if(m.count(i-j.fi)&&i-j.fi==j.fi)//特判一下相同的{cnt+=m[j.fi]/2*2;}}if(cnt%2==0)//来进行判断是否为偶数ans=max(ans,cnt);}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

B.0！！！！！

B.0！！！！！
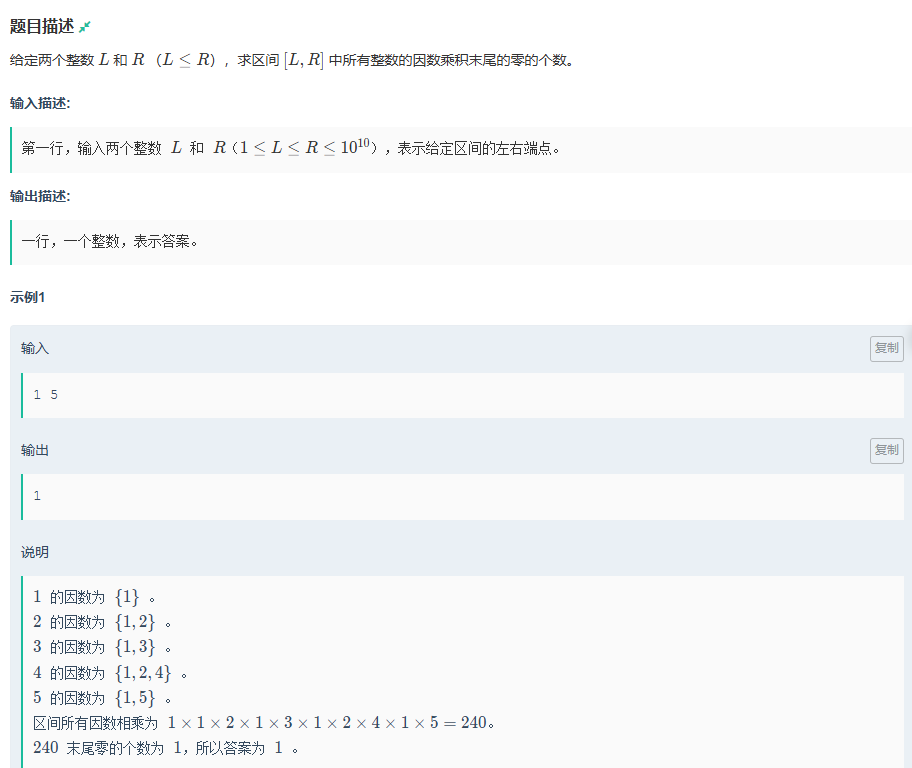
在这里插入图片描述
这一题的公式推导很难懂，该公式的推导
初始的公式：
Fₚ(n) 定义为：满足 px 整除 [1, n] 中所有整数的因数乘积的最大非负整数 x ，
推导初始式子：
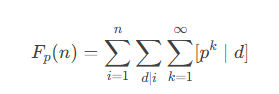
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
解释：如何转化

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll f(ll x,ll lim)
{ll ans=0;for(ll i=x;i<=lim;i*=x){ll n=lim/i;for(ll l=1,r;l<=n;l=r+1){ll k=n/l;r=n/k;ans+=(r-l+1)*k;}}return ans;
}
void solve()
{ll l,r;cin>>l>>r;ll a=f(2,r)-f(2,l-1);ll b=f(5,r)-f(5,l-1);ll ans=min(a,b);cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

C.合并石子

C.合并石子
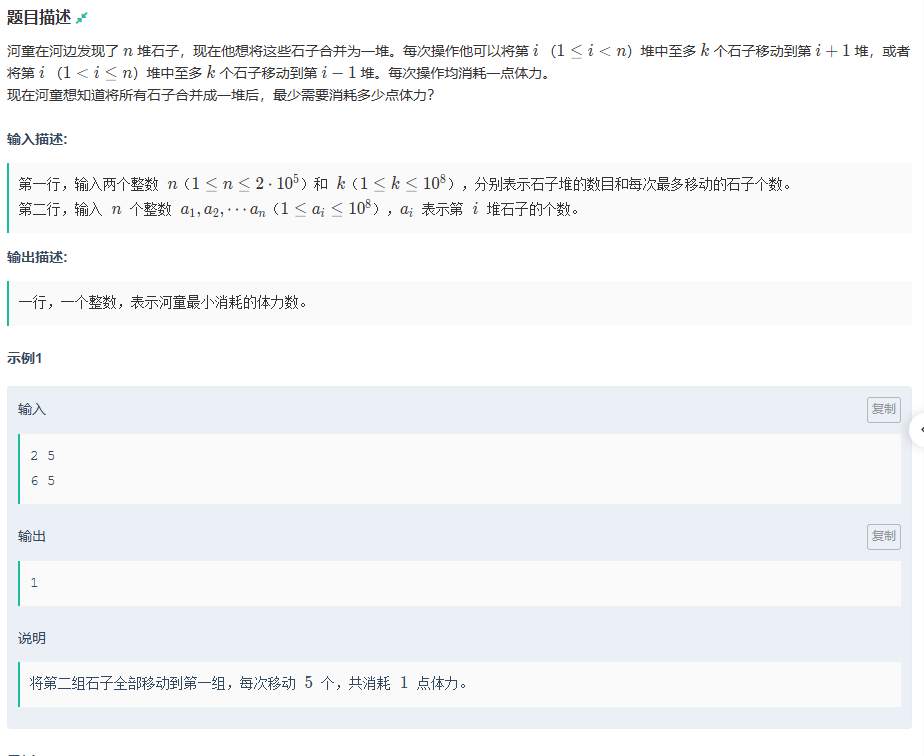
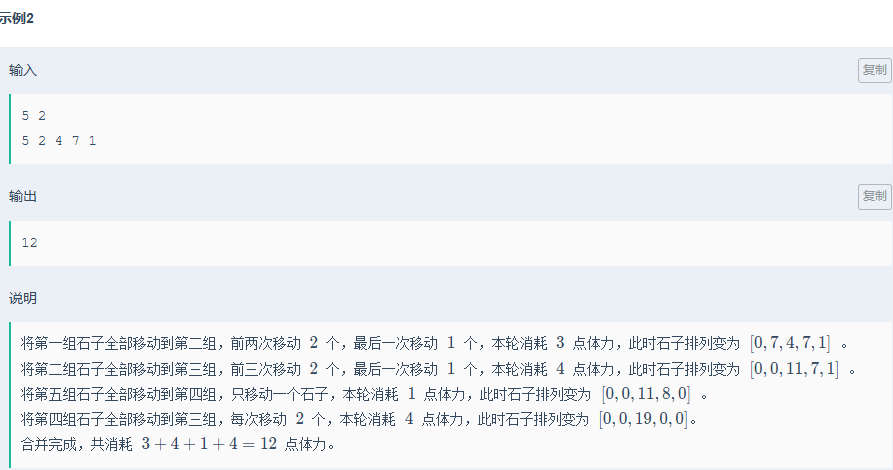
在这里插入图片描述
在这里插入图片描述
从第二个样例不难看出，要想最小，就需要从两边往中间去，当哪边大的话就从另一边开始
以此可以利用前缀与后缀和跑一遍然后取最小，最后再把其中最大值减去
代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll s[N];
ll s1[N];
ll s2[N];
ll sum[N];
void solve()
{ll n,k;cin>>n>>k;for(ll i=1;i<=n;i++){cin>>s[i];s1[i]=s1[i-1]+s[i];//前缀和}if(n==1){cout<<0<<endl;return ;}ll x=1;for(ll i=n;i>=1;i--)//后缀和{s2[i]=s2[i+1]+s[i];}for(ll i=1;i<=n;i++){if(s1[i]%k==0)//判断每一步总共消耗多少s1[i]=s1[i]/k;elses1[i]=s1[i]/k+1;if(s2[i]%k==0)//与上面相同s2[i]=s2[i]/k;elses2[i]=s2[i]/k+1;}for(ll i=1;i<=n;i++){sum[i]=min(s1[i],s2[i]);//取最小的}sort(sum+1,sum+n+1);//排序为了后边去除最大值ll ans=0;for(ll i=1;i<n;i++)//不用加最大值{ans+=sum[i];}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

D.箭头谜题Ⅰ

D.箭头谜题Ⅰ
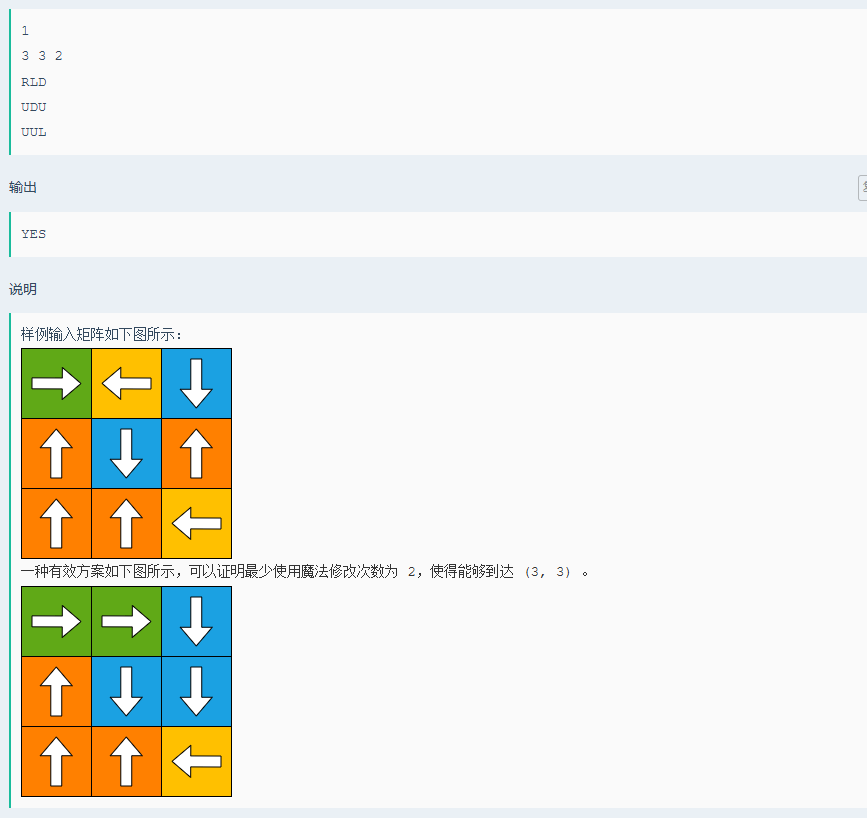
在这里插入图片描述
在这里插入图片描述
咋一看题目无从下手，但是理解本质之后就是BFS找最短路，这里可以运用01BFS来进行遍历，需要运用到双端队列，将不需要消耗的放到队列前端，将需要消耗的放到队列后端，同时遍历的时候，直接记录到当前点所需要的最小花费，
代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
string f="UDLR";
pii df[]={{-1,0},{1,0},{0,-1},{0,1}};//用来遍历与上面的字符串一一对应
struct node
{ll x,y,sp;//x,y是当前坐标，而sp是处于当前坐标的步数
};
const ll N=1e6+10;
void solve()
{ll n,m,k;cin>>n>>m>>k;vector<string>v(n);for(ll i=0;i<n;i++)cin>>v[i];vector<vector<ll>>vis(n,vector<ll>(m,-1));deque<node>p;p.push_front({0,0,0});while(!p.empty()){node sum=p.front();p.pop_front();if(vis[sum.x][sum.y]!=-1)//如果访问过就直接跳过continue;vis[sum.x][sum.y]=sum.sp;for(ll i=0;i<4;i++){ll x=df[i].fi+sum.x;ll y=df[i].se+sum.y;if(x<0||y<0||x>=n||y>=m||vis[x][y]!=-1)continue;if(v[sum.x][sum.y]==f[i])//不消耗的进入前端p.push_front({x,y,sum.sp});else//消耗过的进入后边p.push_back({x,y,sum.sp+1});}}if(vis[n-1][m-1]<=k)cout<<"YES"<<endl;elsecout<<"NO"<<endl;}
signed main()
{IOS;ll t=1;cin>>t;while(t--)solve();return 0;
}

G.封闭运算

G.封闭运算
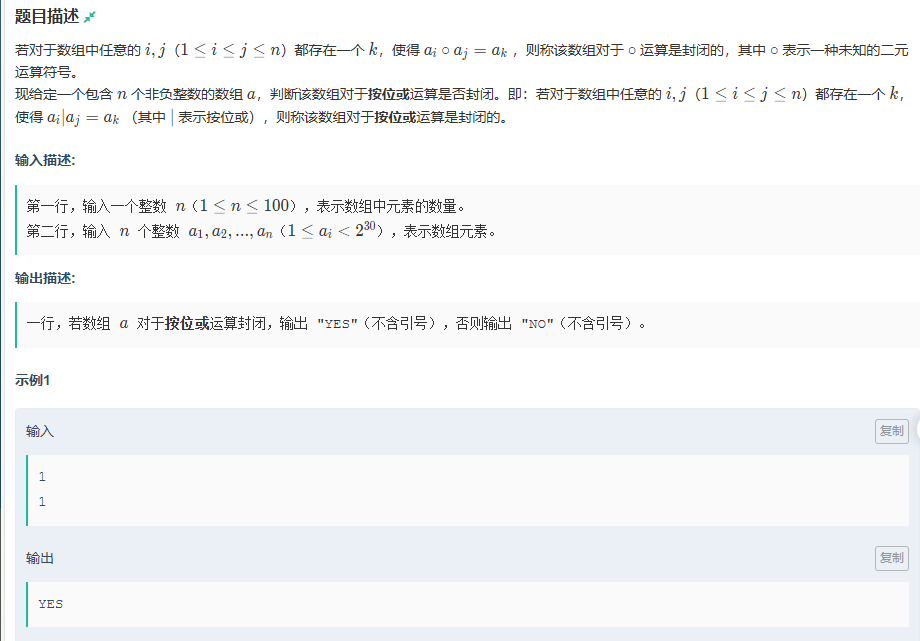
在这里插入图片描述
暴力遍历就行
代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll s[N];
void solve()
{ll n;cin>>n;unordered_map<ll,ll>m;for(ll i=1;i<=n;i++){cin>>s[i];m[s[i]]++;}if(n==1){cout<<"YES"<<endl;return ;}ll sum=0;ll sum1=0;for(ll i=1;i<=n;i++){for(ll j=i;j<=n;j++){ll k=s[i]|s[j];if(!m.count(k)){cout<<"NO"<<endl;return ;}}}cout<<"YES"<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

J.故障机器人的完美牌组

J.故障机器人的完美牌组
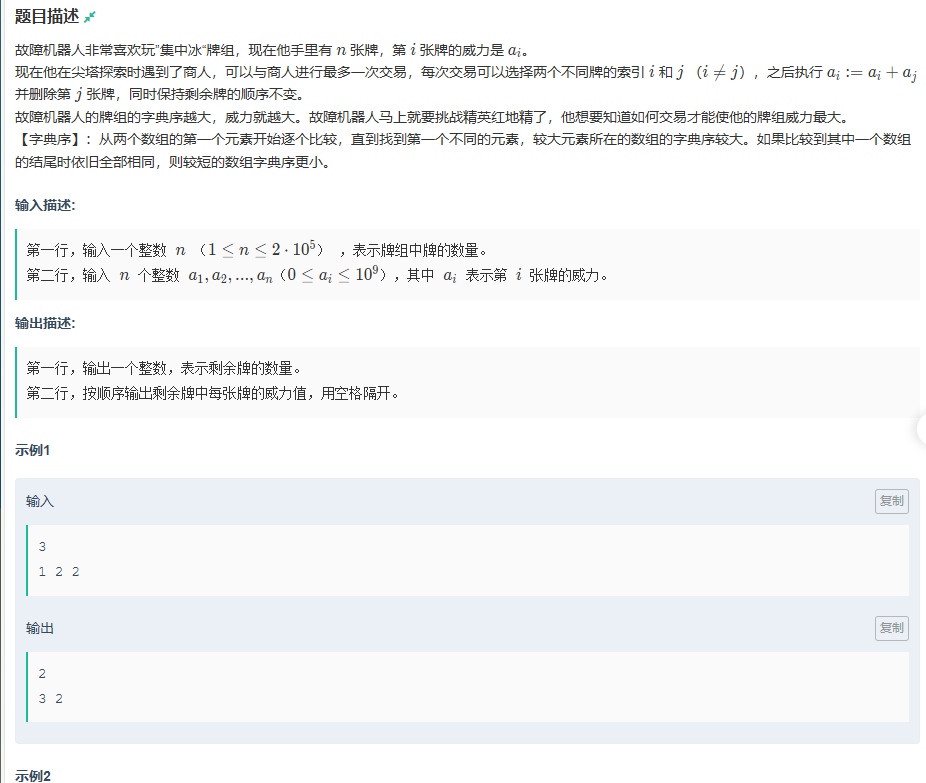
在这里插入图片描述
其这一题才开始没读懂，不知道什么是字典序，看了好长时间才看懂，其实，要想最大就把最大值与当前第一个数结合就行。但是其中有很多细节，
1.就是最大值为0的话，不操作直接输出
2.就是最大值是第一个数时且次大值为0时，也是直接输出不操作
3.就是最大值是第一个且次大值不为0就把第一个与次大值相加，注意如果次大值尽量删除后面的
4.就是最大值不是第一个就直接与最大值相加，同样也要注意尽量删除靠后的。
就是没有注意到删除靠后的才导致错了好多次
代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll n;
ll a[N];
ll b[N];
void solve()
{cin>>n;for(ll i=1;i<=n;i++){cin>>a[i];b[i]=a[i];}if(n==1){cout<<1<<endl;cout<<a[1]<<" ";return; }sort(b+1,b+n+1);if(b[n]==0){cout<<n<<endl;for(ll i=1;i<=n;i++)cout<<a[i]<<" ";return ;}if(a[1]==b[n]&&b[n-1]==0){cout<<n<<endl;for(ll i=1;i<=n;i++)cout<<a[i]<<" ";return ;}if(a[1]==b[n]){cout<<n-1<<endl;ll f=0;cout<<a[1]+b[n-1]<<" ";ll x1=0;for(ll i=1;i<=n;i++){if(a[i]==b[n-1]){x1=i;}}for(ll i=2;i<=n;i++){if(f==0&&i==x1){f=1;continue;}cout<<a[i]<<" ";}}else{cout<<n-1<<endl;ll f=0;cout<<a[1]+b[n]<<" ";ll x1=0;for(ll i=1;i<=n;i++){if(a[i]==b[n]){x1=i;}}for(ll i=2;i<=n;i++){if(f==0&&x1==i){f=1;continue;}cout<<a[i]<<" ";}}}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

L.故障机器人的完美遗物

L.故障机器人的完美遗物
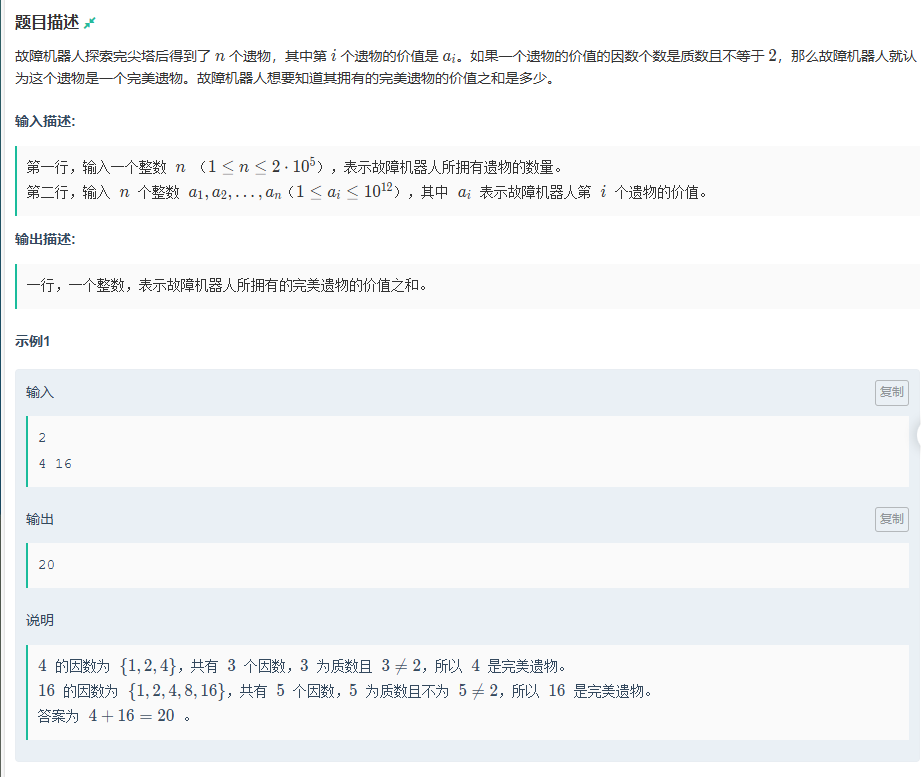
在这里插入图片描述
这一题同样有找规律的部分，通过手写会发现除了那些完全平方数，其他的数的因数的个数肯定是偶数，因为其因数分解是对称的，故其不可能。当然完全平方数的因数为奇数，但奇数不一定为质数，因此只需要解决这一部分就行了

试除法（加上埃氏筛模板）

void pre()
{v[0]=v[1]=1;for(ll i=2;i<=N;i++){if(!v[i])p[cnt++]=i;for(ll j=0;j<=cnt&&i*p[j]<=N;j++){v[i*p[j]]=1;if(i%p[j]==0)break;}}
}
ll sc(ll num)
{ll ans=1;for(ll i=0;i<cnt;i++){ll sum=0;if(p[i]*p[i]>num)break;while(num%p[i]==0){num/=p[i];sum++;}ans*=(sum+1);if(num<p[i])break;}if(num!=1)ans*=2;//处理剩余质因数（1+1）return ans;
}

在这里插入图片描述
利用平方根

void pre()
{v[0]=v[1]=1;for(ll i=2;i<=N;i++){if(!v[i])p[cnt++]=i;for(ll j=0;j<=cnt&&i*p[j]<=N;j++){v[i*p[j]]=1;if(i%p[j]==0)break;}}
}
ll sc(ll num)
{ll ans=1;for(ll i=0;i<cnt;i++){ll sum=0;if(p[i]*p[i]>num)break;while(num%p[i]==0){num/=p[i];sum++;}ans*=(sum*2+1);if(num<p[i])break;}if(num!=1)ans*=3;//处理剩余质因数（1x2+1）return ans;
}

在这里插入图片描述
代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+5000;
ll cnt=0;
ll p[N];//存储筛出的质数
ll v[N];//当是0的时候则是质数
void pre()//埃氏筛模板
{v[0]=v[1]=1;for(ll i=2;i<=N;i++){if(!v[i])p[cnt++]=i;for(ll j=0;j<=cnt&&i*p[j]<=N;j++){v[i*p[j]]=1;if(i%p[j]==0)break;}}
}
ll sc(ll num)//试除法求因数
{ll ans=1;for(ll i=0;i<cnt;i++){ll sum=0;if(p[i]*p[i]>num)break;//记得提前剪切优化while(num%p[i]==0){num/=p[i];sum++;}ans*=(sum*2+1);//公式推理，由于是平方根if(num<p[i])break;}if(num>1)ans*=3;//处理剩余的质因数return ans;
}
void solve()
{pre();ll n;cin>>n;ll ans=0;for(ll i=1;i<=n;i++){ll a;cin>>a;if(a<=2)continue;ll k=sqrt(a);if(k*k==a){ll c=sc(k);if(v[c]==0&&c>2)ans+=a;}}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)solve();return 0;
}

总结

这场感觉数论知识不少，而且有太多细节了。又学到新知识了

http://www.dtcms.com/a/319938.html

相关文章：

  • 北京JAVA基础面试30天打卡04
  • 一文入门 matplotlib：从基础图表到数据可视化初体验
  • git branch -a无法查看最新的分支
  • CNB私有化部署Dify(零成本）教程
  • 操作系统1.4：操作系统的体系结构
  • ollama 运行gpt-oss 系列教程
  • Numpy科学计算与数据分析：Numpy数组创建与应用入门
  • DevOps简单教程应用
  • ⭐CVPR2025 RoboBrain：机器人操作的统一大脑模型[特殊字符]
  • Redis（八）：Redis高并发高可用（哨兵Sentinel）
  • 上海一家机器人IPO核心零部件依赖外购， 募投计划频繁修改引疑
  • QDataStream入门
  • Redis实战（8） -- 分布式锁Redission底层机制
  • 如何解决用阿里云效流水线持续集成部署Nuxt静态应用时流程卡住，进行不下去的问题
  • 基于 MATLAB 的 QPSK 调制、解调、通过高斯信道的误码率计算，并绘制误码率图和眼图、星座图
  • 火山引擎接入豆包AI（纯前端调用api的方式）
  • Java 大视界 -- Java 大数据在智能教育在线课程互动优化与学习体验提升中的应用（386）
  • E频段芯片解决方案
  • npm 与 npx 区别详解。以及mcp中npx加载原理。
  • 2025年生成式大模型部署与推理优化全景解析
  • 14天搞定Excel公式：告别加班，效率翻倍！
  • 【YOLOv8改进 - 上采样】EUCB:(Efficient Up-convolution Block，高效上卷积块）实现特征图尺度匹配和高效上采样
  • 网络编程基石：域名系统与默认端口号详解
  • 文章采集发布Destoon网站技巧
  • C语言函数与预编译：模块化编程的精髓
  • 【AI论文】细胞锻造（CellForge）：虚拟细胞模型的智能体化设计
  • 上岸AAAI 2025：自适应框架+前沿算法，顶会热点方向
  • 【VLLM篇】：原理-实现
  • 【论文阅读】基于元模型的体系知识图谱构建
  • spring boot学习计划