当前位置： 首页 > news >正文

《Day3-PyTorch 自动微分入门：从计算图到梯度下降的实践指南》

news 2025/8/8 8:28:30

八、自动微分

        自动微分模块torch.autograd负责自动计算张量操作的梯度，具有自动求导功能。自动微分模块是构成神经网络训练的必要模块，可以实现网络权重参数的更新，使得反向传播算法的实现变得简单而高效。

1. 基础概念

张量

        Torch中一切皆为张量，属性requires_grad决定是否对其进行梯度计算。默认是 False，如需计算梯度则设置为True。

计算图：

        torch.autograd通过创建一个动态计算图来跟踪张量的操作，每个张量是计算图中的一个节点，节点之间的操作构成图的边。

        在 PyTorch 中，当张量的 requires_grad=True 时，PyTorch 会自动跟踪与该张量相关的所有操作，并构建计算图。每个操作都会生成一个新的张量，并记录其依赖关系。当设置为 True 时，表示该张量在计算图中需要参与梯度计算，即在反向传播（Backpropagation）过程中会自动计算其梯度；当设置为 False 时，不会计算梯度。

例如：
z = x * y

                                                loss = z.sum()

        在上述代码中，x 和 y 是输入张量，即叶子节点，z 是中间结果，loss 是最终输出。每一步操作都会记录依赖关系：

z = x * y：z 依赖于 x 和 y。

loss = z.sum()：loss 依赖于 z。

这些依赖关系形成了一个动态计算图，如下所示：

x       y\     /\   /\ /z||vloss

叶子节点：

在 PyTorch 的自动微分机制中，叶子节点（leaf node） 是计算图中：

  • 由用户直接创建的张量，并且它的 requires_grad=True。
  •  这些张量是计算图的起始点，通常作为模型参数或输入变量。

特征：

  • 没有由其他张量通过操作生成。

  • 如果参与了计算，其梯度会存储在 leaf_tensor.grad 中。

  • 默认情况下，叶子节点的梯度不会自动清零，需要显式调用 optimizer.zero_grad() 或 x.grad.zero_() 清除。

如何判断一个张量是否是叶子节点？

通过 tensor.is_leaf 属性，可以判断一个张量是否是叶子节点。

x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)  # 叶子节点
y = x ** 2  # 非叶子节点（通过计算生成）
z = y.sum()
​
print(x.is_leaf)  # True
print(y.is_leaf)  # False
print(z.is_leaf)  # False

叶子节点与非叶子节点的区别

特性叶子节点非叶子节点
创建方式用户直接创建的张量通过其他张量的运算生成
is_leaf 属性TrueFalse
梯度存储梯度存储在 .grad 属性中梯度不会存储在 .grad，只能通过反向传播传递
是否参与计算图是计算图的起点是计算图的中间或终点
删除条件默认不会被删除在反向传播后，默认被释放（除非 retain_graph=True）

detach()：张量 x 从计算图中分离出来，返回一个新的张量，与 x 共享数据，但不包含计算图（即不会追踪梯度）。

特点：

  • 返回的张量是一个新的张量，与原始张量共享数据。

  • 对 x.detach() 的操作不会影响原始张量的梯度计算。

  • 推荐使用 detach()，因为它更安全，且在未来版本的 PyTorch 中可能会取代 data。

import torch
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x.detach()  # y 是一个新张量，不追踪梯度
​
y += 1  # 修改 y 不会影响 x 的梯度计算
print(x)  # tensor([1., 2., 3.], requires_grad=True)
print(y)  # tensor([2., 3., 4.])

反向传播

        使用tensor.backward()方法执行反向传播，从而计算张量的梯度。这个过程会自动计算每个张量对损失函数的梯度。例如：调用 loss.backward() 从输出节点 loss 开始，沿着计算图反向传播，计算每个节点的梯度。

梯度

        计算得到的梯度通过tensor.grad访问，这些梯度用于优化模型参数，以最小化损失函数。

2. 计算梯度

使用tensor.backward()方法执行反向传播，从而计算张量的梯度

2.1 标量梯度计算

参考代码如下：

import torch
​
​
def test001():# 1. 创建张量：必须为浮点类型x = torch.tensor(1.0, requires_grad=True)
​
​# 2. 操作张量y = x ** 2
​# 3. 计算梯度，也就是反向传播y.backward()
​# 4. 读取梯度值print(x.grad)  # 输出: tensor(2.)
​
​
if __name__ == "__main__":test001()
​

2.2 向量梯度计算

案例：

def test003():# 1. 创建张量：必须为浮点类型x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
​# 2. 操作张量y = x ** 2
​# 3. 计算梯度，也就是反向传播y.backward()
​# 4. 读取梯度值print(x.grad)
​
​
if __name__ == "__main__":test003()

错误预警：RuntimeError: grad can be implicitly created only for scalar outputs

由于 y 是一个向量，我们需要提供一个与 y 形状相同的向量作为 backward() 的参数，这个参数通常被称为 梯度张量（gradient tensor），它表示 y 中每个元素的梯度。

def test003():# 1. 创建张量：必须为浮点类型x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
​# 2. 操作张量y = x ** 2
​# 3. 计算梯度，也就是反向传播#反向传播默认输出是标量，如果输出是向量可以在backward()进行梯度张量初始化y.backward(torch.tensor([1.0, 1.0, 1.0]))
​# 4. 读取梯度值print(x.grad)# 输出# tensor([2., 4., 6.])
​
​
if __name__ == "__main__":test003()

我们也可以将向量 y 通过一个标量损失函数（如 y.mean()）转换为一个标量，反向传播时就不需要提供额外的梯度向量参数了。这是因为标量的梯度是明确的，直接调用 .backward() 即可。

import torch
​
​
def test002():# 1. 创建张量：必须为浮点类型x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
​# 2. 操作张量y = x ** 2
​# 3. 损失函数loss = y.mean()
​# 4. 计算梯度，也就是反向传播loss.backward()
​# 5. 读取梯度值print(x.grad)
​
​
if __name__ == "__main__":test002()
​

2.3 多标量梯度计算

参考代码如下

import torch
​
​
def test003():# 1. 创建两个标量x1 = torch.tensor(5.0, requires_grad=True, dtype=torch.float64)x2 = torch.tensor(3.0, requires_grad=True, dtype=torch.float64)
​# 2. 构建运算公式y = x1**2 + 2 * x2 + 7# 3. 计算梯度，也就是反向传播y.backward()# 4. 读取梯度值print(x1.grad, x2.grad)# 输出：# tensor(10., dtype=torch.float64) tensor(2., dtype=torch.float64)
​
​
if __name__ == "__main__":test003()
​

2.4 多向量梯度计算

代码参考如下

import torch
​
​
def test004():# 创建两个张量，并设置 requires_grad=Truex = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)y = torch.tensor([4.0, 5.0, 6.0], requires_grad=True)
​# 前向传播：计算 z = x * yz = x * y
​# 前向传播：计算 loss = z.sum()loss = z.sum()
​# 查看前向传播的结果print("z:", z)  # 输出: tensor([ 4., 10., 18.], grad_fn=<MulBackward0>)print("loss:", loss)  # 输出: tensor(32., grad_fn=<SumBackward0>)
​# 反向传播：计算梯度loss.backward()
​# 查看梯度print("x.grad:", x.grad)  # 输出: tensor([4., 5., 6.])print("y.grad:", y.grad)  # 输出: tensor([1., 2., 3.])
​
​
if __name__ == "__main__":test004()
​

3. 梯度上下文控制

梯度计算的上下文控制和设置对于管理计算图、内存消耗、以及计算效率至关重要。下面我们学习下Torch中与梯度计算相关的一些主要设置方式。

3.1 控制梯度计算

梯度计算是有性能开销的，有些时候我们只是简单的运算，并不需要梯度

默认情况下叶子节点的梯度不会自动清零，会累加

import torch
​
​
def test001():x = torch.tensor(10.5, requires_grad=True)print(x.requires_grad)  # True
​# 1. 默认y的requires_grad=True,# y默认也会参与梯度计算，但不是保存该梯度值y = x**2 + 2 * x + 3print(y.requires_grad)  # True
​# 2. 如果不需要y计算梯度-with进行上下文管理with torch.no_grad():y = x**2 + 2 * x + 3print(y.requires_grad)  # False
​# 3. 如果不需要y计算梯度-使用装饰器@torch.no_grad()def y_fn(x):return x**2 + 2 * x + 3
​y = y_fn(x)print(y.requires_grad)  # False
​# 4. 如果不需要y计算梯度-全局设置，需要谨慎torch.set_grad_enabled(False)y = x**2 + 2 * x + 3print(y.requires_grad)  # False
​
​
if __name__ == "__main__":test001()
​

3.2 累计梯度

默认情况下，当我们重复对一个自变量进行梯度计算时，梯度是累加的

默认情况下叶子节点的梯度不会自动清零，会累加

import torch
​
​
def test002():# 1. 创建张量：必须为浮点类型x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)
​# 2. 累计梯度：每次计算都会累计梯度for i in range(3):y = x**2 + 2 * x + 7z = y.mean()z.backward()print(x.grad)
​
​
if __name__ == "__main__":test002()
​

输出结果：

tensor([1.3333, 2.0000, 4.2000])
tensor([2.6667, 4.0000, 8.4000])
tensor([ 4.0000,  6.0000, 12.6000])

思考：如果把 y = x**2 + 2 * x + 7放在循环外，会是什么结果？

会报错：

RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.

PyTorch 的自动求导机制在调用 backward() 时，会计算梯度并将中间结果存储在计算图中。默认情况下，这些中间结果在第一次调用 backward() 后会被释放，以节省内存。如果再次调用 backward()，由于中间结果已经被释放，就会抛出这个错误。

3.3 梯度清零

大多数情况下是不需要梯度累加的，奇葩的事情还是需要解决的~

import torch
​
​
def test002():# 1. 创建张量：必须为浮点类型x = torch.tensor([1.0, 2.0, 5.3], requires_grad=True)
​# 2. 累计梯度：每次计算都会累计梯度for i in range(3):y = x**2 + 2 * x + 7z = y.mean()# 2.1 反向传播之前先对梯度进行清零#获取当前轮次的梯度，不是累加值# 自动清零一般放在反向传播之前if x.grad is not None:x.grad.zero_()z.backward()print(x.grad)
​
​
if __name__ == "__main__":test002()# 输出：
# tensor([1.3333, 2.0000, 4.2000])
# tensor([1.3333, 2.0000, 4.2000])
# tensor([1.3333, 2.0000, 4.2000])
​

3.4 案例1-求函数最小值

通过梯度下降找到函数最小值

import torch
from matplotlib import pyplot as plt
import numpy as np
​
​
def test01():x = np.linspace(-10, 10, 100)y = x ** 2
​plt.plot(x, y)
​plt.show()
​
​
def test02():# 初始化自变量Xx = torch.tensor([3.0], requires_grad=True, dtype=torch.float)# 迭代轮次epochs = 50# 学习率lr = 0.1
​list = []for i in range(epochs):# 计算函数表达式y = x ** 2
​# 梯度清零if x.grad is not None:x.grad.zero_()# 反向传播y.backward()# 梯度下降，不需要计算梯度，为什么？# 设置不参与梯度计算with torch.no_grad():#原地修改# 不能使用 x = x - lr * x.grad这个是复制x -= lr * x.grad
​print('epoch:', i, 'x:', x.item(), 'y:', y.item())list.append((x.item(), y.item()))
​# 散点图，观察收敛效果x_list = [l[0] for l in list]y_list = [l[1] for l in list]
​plt.scatter(x=x_list, y=y_list)plt.show()
​
​
if __name__ == "__main__":test01()test02()
​

代码解释：

# 梯度下降，不需要计算梯度
with torch.no_grad():x -= lr * x.grad

如果去掉梯度控制会有什么结果？

代码中去掉梯度控制会报异常：

RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.

因为代码中x是叶子节点(叶子张量)，是计算图的开始节点，并且设置需要梯度。在pytorch中不允许对需要梯度的叶子变量进行原地操作。因为这会破坏计算图，导致梯度计算错误。

在代码中，x 是一个叶子变量（即直接定义的张量，而不是通过其他操作生成的张量），并且设置了 requires_grad=True，因此不能直接通过 -= 进行原地更新。

解决方法

为了避免这个错误，可以使用以下两种方法：

方法 1：使用 torch.no_grad() 上下文管理器

在更新参数时，使用 torch.no_grad() 禁用梯度计算，然后通过非原地操作更新参数。

with torch.no_grad():a -= lr * a.grad

方法 2：使用 data 属性或detach()

通过 x.data 访问张量的数据部分（不涉及梯度计算），然后进行原地操作。

x.data -= lr * x.grad

x.data返回一个与 a 共享数据的张量，但不包含计算图

特点：

  • 返回的张量与原始张量共享数据。

  • 对 x.data 的操作是原地操作（in-place），可能会影响原始张量的梯度计算。

  • 不推荐使用 data，因为它可能会导致意外的行为（如梯度计算错误）。

能不能将代码修改为：

x = x - lr * x.grad

答案是不能，以上代码中=左边的x变量是由右边代码计算得出的，就不是叶子节点了，从计算图中被剥离出来后没有了梯度，报错：

RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

总结：以上方均不推荐，正确且推荐的做法是使用优化器，优化器后续会讲解。

3.5 案例2-函数参数求解

import torch
​
def test02():# 定义数据x = torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)y = torch.tensor([3, 5, 7, 9, 11], dtype=torch.float)
​# 定义模型参数 a 和 b，并初始化a = torch.tensor([1], dtype=torch.float, requires_grad=True)b = torch.tensor([1], dtype=torch.float, requires_grad=True)# 学习率lr = 0.1# 迭代轮次epochs = 100
​for epoch in range(epochs):
​
​# 前向传播：计算预测值 y_predy_pred = a * x + b
​# 定义损失函数loss = ((y_pred - y) ** 2).mean()
​if a.grad is not None and b.grad is not None:a.grad.zero_()b.grad.zero_()
​# 反向传播：计算梯度loss.backward()
​# 梯度下降with torch.no_grad():a -= lr * a.gradb -= lr * b.grad
​if (epoch + 1) % 10 == 0:print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')
​print(f'a: {a.item()}, b: {b.item()}')
​
​
if __name__ == '__main__':test02()
​

代码逻辑：

在 PyTorch 中，所有的张量操作都会被记录在一个计算图中。对于代码：

y_pred = a * x + b
loss = ((y_pred - y) ** 2).mean()

计算图如下：

a → y_pred → loss
x ↗
b ↗

  • a 和 b 是需要计算梯度的叶子张量（requires_grad=True）。

  • y_pred 是中间结果，依赖于 a 和 b。

  • loss 是最终的标量输出，依赖于 y_pred。

当调用 loss.backward() 时，PyTorch 会从 loss 开始，沿着计算图反向传播，计算 loss 对每个需要梯度的张量（如 a 和 b）的梯度。

1、计算 loss 对 y_pred 的梯度：

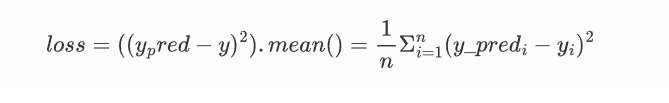
求损失函数关于 y_pred 的梯度（即偏导数组成的向量）。由于 loss 是 y_pred 的函数，我们需要对每个y_pred_i求偏导数，并将它们组合成一个向量。

应用链式法则和常数求导规则，对于每个 (y_pred_i − y_i)^2 项，梯度向量的每个分量是：

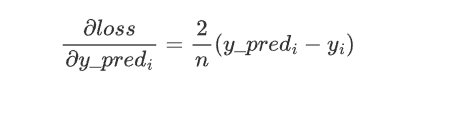
将结果组合成一个向量，我们得到：

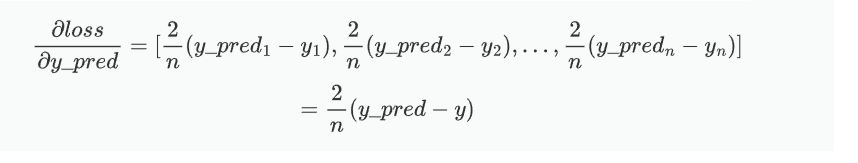
其中n=5，y_pred和y均为向量。

2、计算 y_pred 对 a 和 b 的梯度：

y_pred = a * x + b

对 a 求导：x，x为向量

对 b 求导：1

3、根据链式法则，loss 对 a 的梯度为：

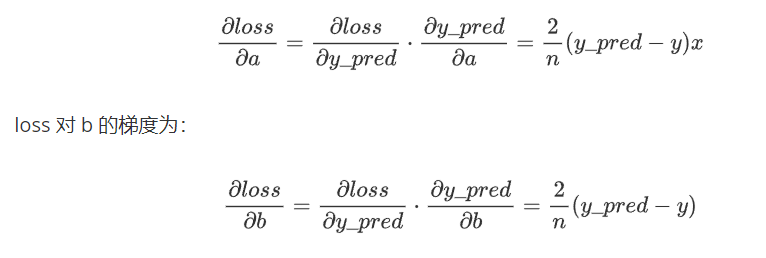
代码运行结果：

Epoch [10/100], Loss: 3020.7896
Epoch [20/100], Loss: 1550043.3750
Epoch [30/100], Loss: 795369408.0000
Epoch [40/100], Loss: 408125767680.0000
Epoch [50/100], Loss: 209420457869312.0000
Epoch [60/100], Loss: 107459239932329984.0000
Epoch [70/100], Loss: 55140217861896667136.0000
Epoch [80/100], Loss: 28293929961149737992192.0000
Epoch [90/100], Loss: 14518387713533614273593344.0000
Epoch [100/100], Loss: 7449779870375595263567855616.0000
a: -33038608105472.0, b: -9151163924480.0

损失函数在训练过程中越来越大，表明模型的学习过程出现了问题。这是因为学习率（Learning Rate）过大，参数更新可能会“跳过”最优值，导致损失函数在最小值附近震荡甚至发散。

解决方法：调小学习率，将lr=0.01

代码运行结果：

Epoch [10/100], Loss: 0.0965
Epoch [20/100], Loss: 0.0110
Epoch [30/100], Loss: 0.0099
Epoch [40/100], Loss: 0.0092
Epoch [50/100], Loss: 0.0086
Epoch [60/100], Loss: 0.0081
Epoch [70/100], Loss: 0.0075
Epoch [80/100], Loss: 0.0071
Epoch [90/100], Loss: 0.0066
Epoch [100/100], Loss: 0.0062
a: 1.9492162466049194, b: 1.1833451986312866

可以看出loss损失函数值在收敛，a接近2，b接近1

将epochs=500

代码运行结果：

Epoch [440/500], Loss: 0.0006
Epoch [450/500], Loss: 0.0006
Epoch [460/500], Loss: 0.0005
Epoch [470/500], Loss: 0.0005
Epoch [480/500], Loss: 0.0005
Epoch [490/500], Loss: 0.0004
Epoch [500/500], Loss: 0.0004
a: 1.986896276473999, b: 1.0473089218139648

a已经无限接近2，b无限接近1

总结

PyTorch 的自动微分模块torch.autograd是实现神经网络训练的核心工具，其核心功能是自动计算张量操作的梯度，支撑反向传播算法以更新模型参数。本文从基础概念、梯度计算方法、梯度上下文控制到实际案例，系统梳理了自动微分的核心逻辑：

  1. 基础概念

    • 张量与 requires_grad：张量通过requires_grad属性控制是否参与梯度计算（默认 False），需计算梯度时设为 True。
    • 计算图：动态构建的有向图，节点为张量，边为操作，记录张量依赖关系以支持反向传播。
    • 叶子节点：用户直接创建且requires_grad=True的张量（is_leaf=True），是计算图起点，梯度存储在.grad中；非叶子节点由运算生成，梯度不存储且反向传播后默认释放。
    • detach()：将张量从计算图分离，返回共享数据但不追踪梯度的新张量。
    • 反向传播与梯度：通过tensor.backward()触发反向传播，计算梯度；梯度通过tensor.grad访问，用于参数优化。

  2. 梯度计算方法

    • 标量梯度：输出为标量时，直接调用backward()即可计算梯度。
    • 向量梯度：输出为向量时，需传入与向量同形的梯度张量（如torch.tensor([1.0,1.0,1.0])），或通过mean()等转换为标量后再调用backward()。
    • 多变量梯度：无论是多标量还是多向量，通过构建计算图后反向传播，可同时计算多个变量的梯度。

  3. 梯度上下文控制

    • 禁用梯度计算：通过with torch.no_grad()、@torch.no_grad()装饰器或全局torch.set_grad_enabled(False)，减少不必要的性能开销。
    • 梯度累加与清零：默认梯度会累加，需通过tensor.grad.zero_()手动清零，确保每轮梯度计算准确。
    • 叶子节点更新：更新叶子节点（如模型参数）时需禁用梯度计算（如with torch.no_grad()），避免破坏计算图。

  4. 实践案例

    • 函数最小值求解：通过梯度下降迭代更新自变量，逐步收敛到函数最小值。
    • 线性回归参数求解：基于损失函数反向传播，优化参数拟合数据，验证了学习率对收敛的关键影响（过大导致发散，过小收敛缓慢）。
http://www.dtcms.com/a/319624.html

相关文章：

  • Redis中间件（三）：Redis存储原理与数据模型
  • Dokcer创建中间件环境
  • LeetCode:347.前K个高频元素
  • 手写数字识别实战 - 从传统机器学习到深度学习
  • 13-netty基础-手写rpc-消费方生成代理-05
  • Qt——入门
  • 数据赋能（386）——数据挖掘——迭代过程
  • Spring、Spring MVC、MyBatis 和 Spring Boot的关系
  • Ethereum：如何优雅部署 NPM 包中的第三方智能合约？
  • LoadBalancingSpi
  • Beelzebub靶机
  • MyCAT实战环节
  • 动手学深度学习13.10. 转置卷积 -笔记练习（PyTorch）
  • 在新建word中使用以前文件中的列表样式
  • Python调用Shell指令的方法与实践
  • 深海中的类型晨曦
  • Jmeter使用第一节-认识面板（Mac版）
  • 初识C++类的6个默认成员函数
  • 以复合赋值运算符（op=）优化单独运算符（op）的实现
  • BKP 与 RTC 时钟
  • 从Text2SQL到Text2Metrics：衡石指标管理技术跃迁
  • 【Bluedroid】蓝牙音频接收端活动设备切换机制深度解析(sink_set_active_device)
  • 密码学侧信道攻击（Side-channel Attack）：从物理泄露中窃取密钥
  • 水库大坝安全监测系统主要概述
  • 护网行动之后：容器安全如何升级？微隔离打造内网“微堡垒”
  • SkyWalking-1--SkyWalking是什么？
  • 基于MATLAB实现支持向量机（SVM）分类
  • `/dev/vdb` 是一个新挂载的 4TB 硬盘，但目前尚未对其进行分区和格式化。
  • WebSocket 在多线程环境下处理 Session并发
  • 多数据中心运维：别让 “分布式” 变成 “混乱式”