嵌入式 - 数据结构：二叉树

目录

一、二叉树的基础概念

1. 从树形结构到二叉树

2. 二叉树的核心术语

二、二叉树的常见类型

1. 按节点结构分类

2. 满二叉树

3. 完全二叉树

三、二叉树的核心操作

1. 节点定义

2. 二叉树的创建

（1）完全二叉树的创建（递归）

（2）非完全二叉树的创建（用户输入）

3. 二叉树的销毁

4. 二叉树的高度计算

四、二叉树的遍历方式

1. 深度优先遍历（DFS）

（1）前序遍历（根左右）

（2）中序遍历（左根右）

（3）后序遍历（左右根）

（4）非递归遍历（借助栈）

2. 广度优先遍历（BFS）：层序遍历

五、二叉树的应用场景

总结

---

在数据结构的世界里，二叉树是一种经典的非线性结构，它以灵活的层次化存储方式，在算法设计、数据检索等领域发挥着不可替代的作用。本文将从基础概念出发，深入解析二叉树的核心特性、常见类型、遍历方式及核心操作，并结合实践代码探讨其应用场景。

一、二叉树的基础概念

1. 从树形结构到二叉树

树形结构是一类重要的非线性结构，它通过 "前驱 - 后继" 关系描述数据间的一对多关联，而二叉树是树形结构中最常用的一种 ——所有节点的度数（后继节点个数）最大为 2。

2. 二叉树的核心术语

• 节点：组成二叉树的基本单元，包含数据及指向子节点的指针。
• 根节点：没有前驱的节点，是树的起点。
• 分支节点：既有前驱又有后继的节点（至少有一个子节点）。
• 叶子节点：没有后继的节点（左右子节点均为空）。
• 层：根节点为第 1 层，其子节点为第 2 层，以此类推。
• 高度：节点高度是由该节点到最远的叶子节点的距离表示该节点高度
• 深度：节点深度是由该节点到根节点的距离表示节点深度
• 树的高度 / 深度：树的高度（或深度）等于层数最多的节点的层数，即从根到最远叶子的距离。
• 树的高度 == 树的深度 == 树的层数
• 度：节点的后继个数（二叉树中节点的度只能是 0、1 或 2）。

二、二叉树的常见类型

1. 按节点结构分类

二叉树的节点可分为四种类型：

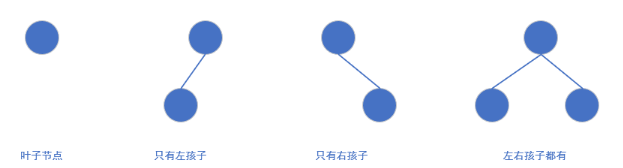
• 叶子节点（度为 0）；
• 只有左孩子的节点（度为 1）；
• 只有右孩子的节点（度为 1）；
• 左右孩子都有的节点（度为 2）。

2. 满二叉树

定义：所有叶子节点均在同一层，且每层节点个数达到最大值（第 k 层有 2^(k-1) 个节点）。
特性：

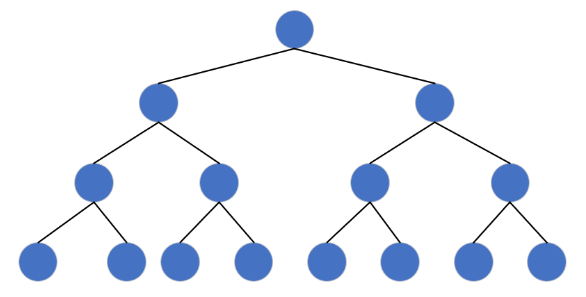
• 第 k 层节点数：2^(k-1)；
• 前 k 层总节点数：2^k - 1。

3. 完全二叉树

定义：节点按 "左孩子编号 = 2n、右孩子编号 = 2n+1" 规则编号后，编号序列是连续的（即除最后一层外，每层节点均满，且最后一层节点靠左排列）。
特性：

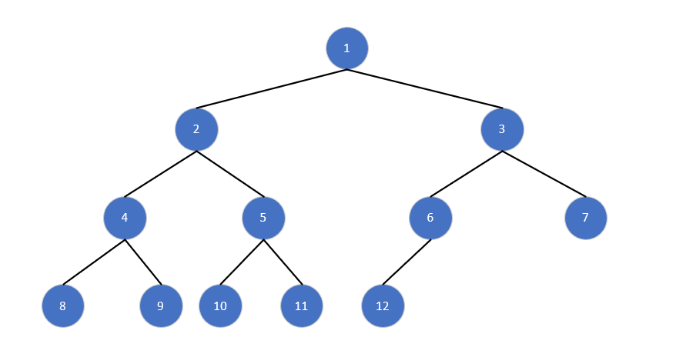
• 对于编号为 i 的节点，若 i>1，则父节点编号为 i//2（向下取整）；
• 若 2i ≤ 总节点数，则左孩子存在；若 2i+1 ≤ 总节点数，则右孩子存在；
• 适合用数组存储（无需存储指针，通过编号计算父子关系）。

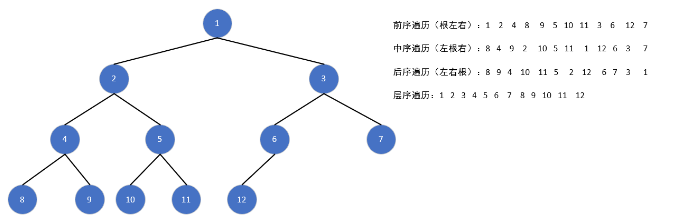
 完全二叉树的遍历形式：

深度优先遍历（DFS）
前序遍历（先序遍历）：根左右
中序遍历：左根右
后序遍历：左右根

广度优先遍历（BFS）
层序遍历：逐层从左到右依次遍历

三、二叉树的核心操作

1. 节点定义

二叉树节点包含数据域和指向左右子节点的指针：

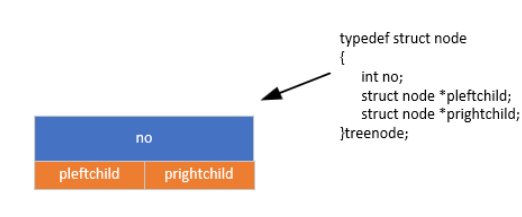
typedef struct node {int no;  // 节点编号（数据域）struct node *pleftchild;  // 左子节点指针struct node *prightchild;  // 右子节点指针
} treenode;

2. 二叉树的创建

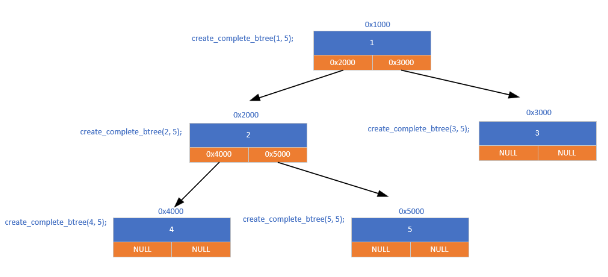
（1）完全二叉树的创建（递归）

根据完全二叉树的编号规则（左孩子 2n，右孩子 2n+1）递归创建：

1. 申请节点空间
2. 存放数据编号
3. 如果存在左子树递归创建左子树
4. 如果存在右子树递归创建右子树

/* 创建完全二叉树 */
treenode *create_complete_btree(int startno, int endno)
{treenode *ptmpnode = NULL;ptmpnode = malloc(sizeof(treenode));if(NULL == ptmpnode){perror("fail to malloc");return NULL;}ptmpnode->no = startno;ptmpnode->pleftchild = ptmpnode->prightchild = NULL;if (2*startno <= endno){ptmpnode->pleftchild = create_complete_btree(2*startno, endno);}if (2*startno + 1 <= endno){ptmpnode->prightchild = create_complete_btree(2*startno+1, endno);}return ptmpnode;
}

（2）非完全二叉树的创建（用户输入）

通过用户输入决定节点是否存在（'#' 表示空节点）：

非完全二叉树，每个结构不一定相同，所以需要从终端接收用户输入决定二叉树的创

/* 创建非完全二叉树 */
treenode *create_btree(void)
{char ch = 0;treenode *ptmpnode = NULL;scanf(" %c", &ch);if ('#' == ch){return NULL;}ptmpnode = malloc(sizeof(treenode));if (NULL == ptmpnode){perror("fail to malloc");return NULL;}ptmpnode->data = ch;ptmpnode->pleftchild = create_btree();ptmpnode->prightchild = create_btree();return ptmpnode;
}

3. 二叉树的销毁

采用后序遍历逻辑（先销毁子树，再销毁自身）：

int destroy_btree(treenode *proot) {if (proot->pleftchild) {destroy_btree(proot->pleftchild);  // 销毁左子树}if (proot->prightchild) {destroy_btree(proot->prightchild);  // 销毁右子树}free(proot);  // 销毁当前节点return 0;
}

4. 二叉树的高度计算

树的高度为左右子树高度的最大值加 1（空树高度为 0）：

获得树的高度、深度、层数

/* 获得树的高度、深度、层数 */
int get_bintree_height(treenode *proot)
{int leftheight = 0;int rightheight = 0;if (NULL == proot){return 0;}leftheight = get_bintree_height(proot->pleftchild);rightheight = get_bintree_height(proot->prightchild);return (leftheight > rightheight ? leftheight : rightheight)+1;
}

四、二叉树的遍历方式

遍历是二叉树最核心的操作，通过遍历可按特定顺序访问树中所有节点。常见遍历方式分为深度优先遍历（DFS） 和广度优先遍历（BFS）。

1. 深度优先遍历（DFS）

以 "深入" 为优先，沿着一条路径走到叶子节点后再回溯，包括前序、中序、后序三种方式。

（1）前序遍历（根左右）

顺序：先访问根节点，再遍历左子树，最后遍历右子树。
递归实现：

int preorder_btree(treenode *proot) {printf("%d ", proot->no);  // 访问根if (proot->pleftchild != NULL) {preorder_btree(proot->pleftchild);  // 遍历左子树}if (proot->prightchild != NULL) {preorder_btree(proot->prightchild);  // 遍历右子树}return 0;
}

（2）中序遍历（左根右）

顺序：先遍历左子树，再访问根节点，最后遍历右子树。
递归实现：

int inorder_btree(treenode *proot) {if (proot->pleftchild != NULL) {inorder_btree(proot->pleftchild);  // 遍历左子树}printf("%d ", proot->no);  // 访问根if (proot->prightchild != NULL) {inorder_btree(proot->prightchild);  // 遍历右子树}return 0;
}

（3）后序遍历（左右根）

顺序：先遍历左子树，再遍历右子树，最后访问根节点。
递归实现：

int postorder_btree(treenode *proot) {if (proot->pleftchild != NULL) {postorder_btree(proot->pleftchild);  // 遍历左子树}if (proot->prightchild != NULL) {postorder_btree(proot->prightchild);  // 遍历右子树}printf("%d ", proot->no);  // 访问根return 0;
}

（4）非递归遍历（借助栈）

递归遍历的本质是利用系统栈，非递归实现则需手动维护栈结构：

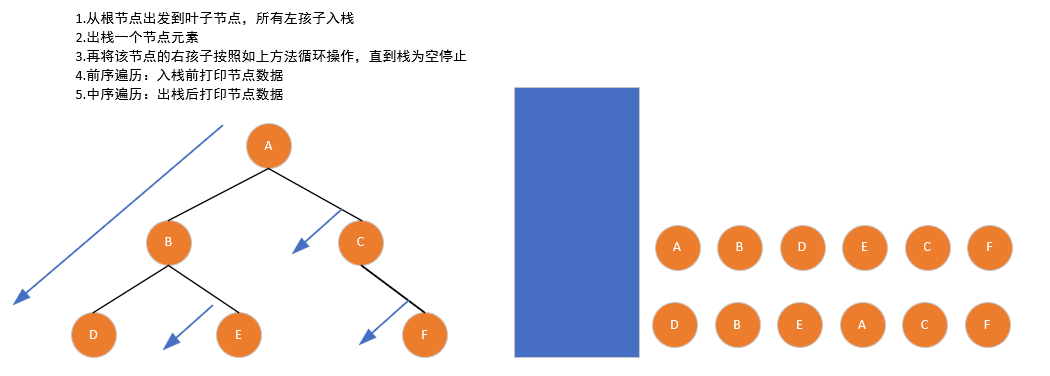
• 前序：入栈前访问根节点，优先将左子树入栈，左子树为空时弹出节点并处理右子树；

/* 非递归前序遍历 */
int preorder_btree_bystack(treenode *proot)
{linknode *ptmpstack = NULL;treenode *ptmpnode = NULL;ptmpstack = create_empty_linkstack();ptmpnode = proot;while (1){while (ptmpnode != NULL){printf("%c ", ptmpnode->data);push_linkstack(ptmpstack, ptmpnode);ptmpnode = ptmpnode->pleftchild;}   if (is_empty_linkstack(ptmpstack)){break;}ptmpnode = pop_linkstack(ptmpstack);ptmpnode = ptmpnode->prightchild;}return 0;
}

• 中序：左子树入栈到底后，弹出节点并访问，再处理右子树；

/* 非递归中序遍历 */
int inorder_btree_bystack(treenode *proot)
{linknode *ptmpstack = NULL;treenode *ptmpnode = NULL;ptmpstack = create_empty_linkstack();ptmpnode = proot;while (1){while (ptmpnode != NULL){push_linkstack(ptmpstack, ptmpnode);ptmpnode = ptmpnode->pleftchild;}   if (is_empty_linkstack(ptmpstack)){break;}ptmpnode = pop_linkstack(ptmpstack);printf("%c ", ptmpnode->data);ptmpnode = ptmpnode->prightchild;}return 0;
}

• 后序：需给节点标记（1 次入栈找右子树，2 次入栈才访问），避免漏访。

1. 因为最后打印根节点，所以根节点需要2次入栈
2. 第一次入栈，是为了出栈时找到该节点的右孩子，找到右孩子后，继续将节点入栈
3. 第二次入栈，是为了打印该节点

/* 非递归后序遍历 */
int postorder_btree_bystack(treenode *proot)
{linknode *ptmpstack = NULL;treenode *ptmpnode = NULL;ptmpstack = create_empty_linkstack();ptmpnode = proot;while (1){while (ptmpnode != NULL){ptmpnode->flag = 1;push_linkstack(ptmpstack, ptmpnode);ptmpnode = ptmpnode->pleftchild;}   if (is_empty_linkstack(ptmpstack)){break;}ptmpnode = pop_linkstack(ptmpstack);if (1 == ptmpnode->flag){ptmpnode->flag = 0;push_linkstack(ptmpstack, ptmpnode);ptmpnode = ptmpnode->prightchild;}else if (0 == ptmpnode->flag){printf("%c ", ptmpnode->data);ptmpnode = NULL;}}return 0;
}

2. 广度优先遍历（BFS）：层序遍历

顺序：从根节点开始，逐层从左到右访问所有节点（借助队列实现）。

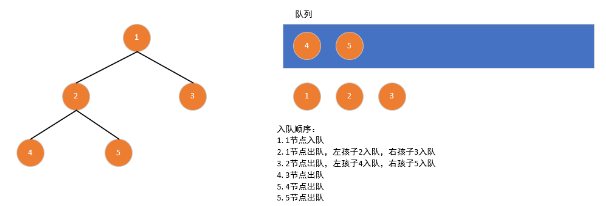
实现代码：

int layoutorder_btree(treenode *proot) {linknode *ptmpqueue = create_empty_linkqueue();  // 创建队列treenode *ptmpnode = NULL;enter_linkqueue(ptmpqueue, proot);  // 根节点入队while (!is_empty_linkqueue(ptmpqueue)) {ptmpnode = quit_linkqueue(ptmpqueue);  // 出队并访问printf("%d ", ptmpnode->no);if (ptmpnode->pleftchild != NULL) {enter_linkqueue(ptmpqueue, ptmpnode->pleftchild);  // 左孩子入队}if (ptmpnode->prightchild != NULL) {enter_linkqueue(ptmpqueue, ptmpnode->prightchild);  // 右孩子入队}}destroy_linkqueue(&ptmpqueue);return 0;
}

五、二叉树的应用场景

1. 二叉搜索树（BST）：左子树节点值均小于根，右子树节点值均大于根，支持高效的插入、删除和查找（平均时间复杂度 O (logn)）。
2. 堆（Heap）：基于完全二叉树实现，分为大根堆（根节点最大）和小根堆（根节点最小），常用于优先队列和排序（堆排序）。
3. 哈夫曼树：带权路径长度最短的二叉树，用于数据压缩（哈夫曼编码）。
4. 表达式树：用于解析数学表达式（如 "(3+4)5" 可表示为根为''，左子树为 '+'，右子树为 5）。

总结

二叉树作为一种灵活的非线性结构，通过层次化的存储方式平衡了数据的访问效率和扩展性。从基础概念到遍历操作，再到实际应用，二叉树的每一个特性都为解决复杂问题提供了思路。掌握二叉树不仅是数据结构学习的关键，更是深入理解算法设计的基础 —— 无论是递归思想的运用，还是栈、队列等辅助结构的配合，都为后续学习更复杂的树结构（如红黑树、B 树）奠定了坚实的基础。