院校机试刷题第二十一天|回顾代码随想录第十六天、

一、代码随想录第十六天

1.513找树左下角的值

递归和迭代（层序）都可解决

层序：找到最后一层的最后一个元素

递归：想要求当前节点为根节点的二叉树最左下角的节点的值，需要求左子树/右子树最左下角的节点，并且比较哪个更深，选择记录更深的那个。这种欲求自己，先求左右子树的解法都可以叫做递归法，需要确定自己本层的处理逻辑，以及左右子树分别的递归逻辑。

层序代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int findBottomLeftValue(TreeNode* root) {int result = 0;queue<TreeNode*> que;if(root != nullptr) {que.push(root);}while(!que.empty()) {int size = que.size();for(int i = 0; i < size; i++) {TreeNode* temp = que.front();que.pop();if(temp->left) que.push(temp->left);if(temp->right) que.push(temp->right);if(i == 0) {result = temp->val;}}}return result;}
};

2.112路径总和

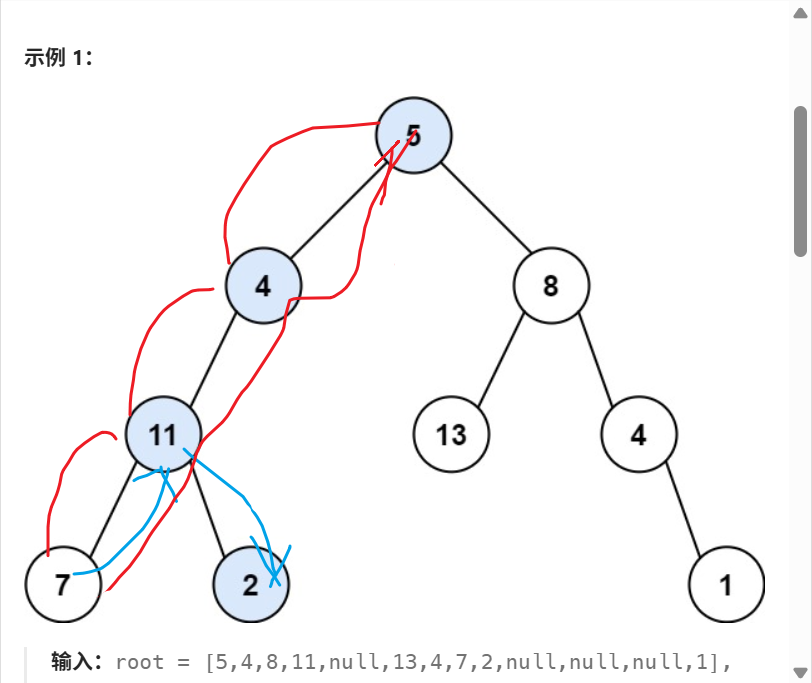
这道题关键的一个点在于回溯，按照“中左右”的顺序遍历时，如果在遍历左或者右的时候出现满足的情况，那么就按照下图红线所示，一路返回true，而不进行任何操作，不用进行回溯；如果在遍历时没有出现满足的情况，那么就按照下图蓝色所示的进行回溯的操作，回溯操作表现为，在返回上一层的时候，目标数发生改变，去除掉下一层对目标数的操作，这种操作可以直接在递归函数的参数中进行相关的操作。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool traverse(TreeNode* root, int targetSum) {if(root->left == nullptr && root->right == nullptr) {if(targetSum == 0) {return true;} else {return false;}}// 左if(root->left) {bool result1 = traverse(root->left, targetSum - (root->left->val));if(result1) return true;}// 右if(root->right) {bool result2 = traverse(root->right, targetSum - (root->right->val));if(result2) return true;}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if(root == nullptr) return false;return traverse(root, targetSum - root->val);}
};

3.113路径总和II 

相比上一题，这个要求的是所有的路径，而不仅仅是true/false，那么就需要一个vector数组来记录路径，一个vector数组来记录所有路径。回溯修改为先将遍历到的节点加入到路径中，然后递归，然后回溯弹出节点。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> result;vector<int> path;void traverse(TreeNode* cur, int target) {//中if(cur->left == nullptr && cur->right == nullptr && target == 0) {result.push_back(path);return;}//左if(cur->left) {path.push_back(cur->left->val);traverse(cur->left, target - cur->left->val);path.pop_back();//回溯！！！这样才可以返回找到别的路径}//右if(cur->right) {path.push_back(cur->right->val);traverse(cur->right, target - cur->right->val);path.pop_back();}return;}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {// result.clear();// path.clear();if(root == nullptr) return result;path.push_back(root->val);traverse(root, targetSum - root->val);return result;}
};

二、303区域和检索

1.解题思路

这里用到了前缀和的思想，求left和right之间的元素的和就是求从头到right的元素和  减去  从头到left的元素和，所以定义一个数组求一下所有的从头到任意一个元素的前缀和即可。注意，这个前缀和数组应该预先定义一项s[0] = 0，这样从left到right就可以用公式s[right + 1] - s[left]这样进行求解了。

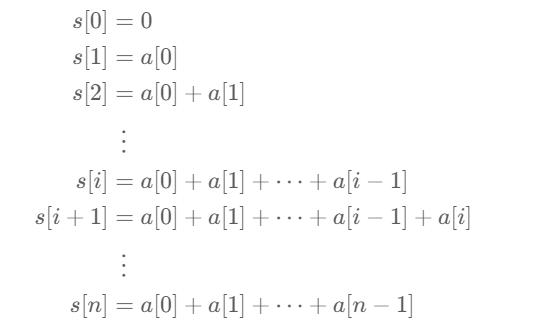
2.代码

class NumArray {
public:vector<int> s;NumArray(vector<int>& nums) {s.resize(nums.size() + 1);s[0] = 0;for(int i = 0; i < nums.size(); i++) {s[i + 1] = s[i] + nums[i];}}int sumRange(int left, int right) {return s[right + 1] - s[left];}
};/*** Your NumArray object will be instantiated and called as such:* NumArray* obj = new NumArray(nums);* int param_1 = obj->sumRange(left,right);*/

二、560和为k的子数组

1.暴力法

暴力法：直接两层for枚举出来所有的子数组，然后一一判断是否和为k，和为k就统计值count++。

但是会超时

class Solution {
public:int subarraySum(vector<int>& nums, int k) {int count = 0;for(int i = 0; i < nums.size(); i++) {int sum = 0;for(int j = i; j < nums.size(); j++) {sum += nums[j];if(sum == k) {count++;}}}return count;}
};

2.前缀和方法

求所有的子序列的和也就是求子序列 从头到j的前缀和 减去 从头到i的前缀和，看有几个满足条件的s[j] - s[i] = k。这个实际上可以转换为依次遍历s中的所有元素，看对于每个元素（也就是可以视为s[j]），在s数组从0-j这部分，到底有几个s[i] = s[j] - k。

所以还需要一个map统计一下每个s的值，以及s数组中有几个这样的值，一边遍历s数组一边进行统计即可，遍历的过程中，该map对应的值++即可。

class Solution {
public:int subarraySum(vector<int>& nums, int k) {int n = nums.size();vector<int> s(n + 1, 0);for(int i = 0; i < nums.size(); i++) {s[i + 1] = s[i] + nums[i];}int ans = 0;unordered_map<int, int> cnt;// 一边遍历前缀和数组，一边统计有多少个前缀和为该数值// s[i] = s[j] - k, k是目标结果，也就是在求有几个s[j] - s[i] = k，这里是先遍历所有的s[j]，求出每个s[j]对应的s[i]，然后看s[j]的前面有几个s[i]，这样进行统计。// 同时在遍历的过程中，也顺便统计s[j]的个数。for(int sj : s) {ans += cnt.contains(sj - k) ? cnt[sj - k] : 0;cnt[sj]++;}return ans;}
};