希尔排序:高效插入排序的进阶之道
希尔排序:高效插入排序的进阶之道
- 基本概念
- 工作原理
- 增量序列的选择
- 实现
- 分析
基本概念
希尔排序(Shell Sort)是插入排序的改进版本,由计算机科学家唐纳德・希尔(Donald Shell)于 1959 年提出。它通过引入「增量序列」的概念,打破了插入排序 “只能相邻元素交换” 的限制,大幅提升排序效率,尤其适合中等规模的数组排序。
与普通插入排序(仅能交换相邻元素)不同,希尔排序先通过 较大的间隔(增量) 对元素 “分组排序”,逐步缩小间隔,最终在间隔为 1 时退化为普通插入排序(此时数组已接近有序,插入排序效率最优)。
工作原理
以该数组为例

-
选择合适的增量序列
确认其为递减的,我通常设置为 gap = n/3+1。该数组中,第一次的 增量序列为3,所以后续我就以gap=3为例讲解过程 -
根据增量序列分组
这一步就是希尔排序的核心,我把间隔为三的元素分为一组,上述数组分组后如下图所示
至此数组被分为三组:[64,12,90],[34,22],[25,11],后面我简称其为增序数组 -
依次进行插入排序
我在排序算法入门:直接插入排序详解一文中详细介绍了插入排序,如果你尚不清楚可以参考这篇文章。这里我还是模拟一次详细过程帮你理解:
我们用变量end表示有序区的最后一个元素,end+gap表示同组增序数组的元素
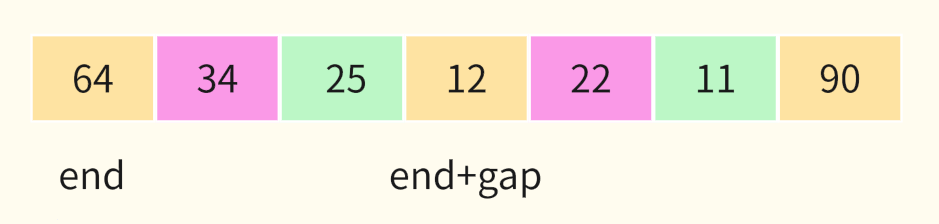
通过逻辑比较,关注end的位置,如其超出数组了代表达到数组头部。
你需要了解直接插入排序才能理解上述过程,因为二者没有区别。 -
缩小增量重复过程
缩小gap的值,直到gap==1时,其就是完全的直接插入排序
增量序列的选择
增量序列的选择有很多,不同的选择会产生不同的时间复杂度,我给出我用过的几种:
- 希尔最初的增量序列
规则:gap = n / 2,每次循环 gap /= 2(如 n=10 时,增量为 5, 2, 1)。
最易理解,但效率不是最优,时间复杂度约为 O(n^2) - Knuth 增量序列
由公式 gap = 3 * gap + 1 生成
使时间复杂度优化至约O(n^1.5),是实践中较常用的序列。 - Sedgewick 增量序列
结合两种模式的序列:D=9∗4^i - 9∗2^i +1 或 4i−3∗2^i+1
理论上时间复杂度接近O(n^1.3)
实现
void ShellSort(int arr[], int n)
{int gap = n;while (gap > 1) // 直到 gap==1 时,为直接插入排序{gap = gap / 3 + 1; // 修改增量序列for (int i = 0; i < n - gap; i++){ int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}
分析
希尔排序是不稳定排序(相同元素的相对位置可能因 “分组排序” 改变),但平均效率优于普通插入排序。
