二分查找

目录

1 二分查找

2 在排序数组中查找元素的第一个和最后一个位置

3 x 的平方根 

4  搜索插入位置

5 山脉数组的峰顶索引

6 寻找峰值

7 寻找旋转排序数组中的最小值 

8 LCR 173. 点名

---

二分查找算法虽然是一个基础的算法，但是它里面有很多细节，我们稍不注意就会写出死循环的代码。我们常说二分查找算法的前提是有序数组，但是其实并不是必要前提，在有些情况下，数据具有二分性时，我们都可以使用二分算法来解决。

二分查找常见的题型：

1、找出有序数组中的某一个值的下标，这种问题是最基础的二分问题，代码一般如下：

class Solution {
public:int search(vector<int>& nums, int key) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] > key)right = mid - 1;else if (nums[mid] < key)left = mid + 1;else return mid;}return -1; }
};

2、查找某个元素在nums出现的第一个位置/找到大于等于key的第一个元素位置

此类题型也称为找左边界的问题，此时我们维护的 left 和 right ，right 始终代表着已确定合法区间的左边界，也就是[right,n-1] 区间一定都是大于等于key的，而left始终标识已确定的不合法区间的右边界的下一个位置，也就是说[0,left)都是已经确定的小于key的元素。而[left,right)区间就是我们未确定的区间。

左边界有两个特性： 左边界以及右边的元素都是大于等于 key 的，左边界左边元素都是小于key的。

那么此时mid位置元素有三种情况：

(1) nums[mid] >= key ， 说明mid以及mid 的后面所有元素都是大于等于key的合法区间，此时可以更新right = mid 。 注意right 不能更新为 mid - 1 ，因为mid - 1 位置是不确定的，有可能小于key，我们要找的是大于等于key的第一个位置。

(2) nums[mid] < key ，说明此时mid以及mid左边的所有元素都是小于key的不合法区间，那么此时可以更新 left = mid + 1，left必须要越过这个不合法区间才有继续查找的意义。

我们查找的区间始终是 [left,right] ，大于等于key的第一个位置只会出现在这个区间内。

那么结束条件就是left = right 的时候，说明找到了左边界。

但是此时有一个问题，mid 的取值时，其实有两种做法：

一种是 mid = left + (right - left) / 2，也就是 mid = (left + right) / 2 ，这种做法下，如果[left,right]有奇数个元素，那么mid标识中间位置，如果为偶数个元素，由于中间位置可以看成有两个，这种求法得出的是两个中间位置的较左值。

另一种是 mid = left + (right - left + 1) / 2 ，也就是 mid = (left + right + 1) / 2，在这种求法下，如果[left,right]有奇数个元素，那么求出的还是中间位置，如果偶数个元素，那么得出的是中间靠右的那个元素。

比如：当 left = 2 , right = 3 时，我们使用第一种求法得出的mid = left ，如果使用第二种方法，那么得出的mid = right。 

那么这两种求法在二分算法中有什么注意的吗？

就拿上面的求左边界的情况来说，我们更新 left = mid + 1，这种情况下，如果我们使用第一种求法，那么 mid = left ， 不管怎么样，left 最终都会和 right 相遇跳出循环。 但是如果我们使用第二种求法，那么 mid = right ，此时mid位置一定是合法的位置，那么更新right = mid ,这样一来就陷入死循环了，每一次循环进来 mid = right ，而后我们又更新 right = mid。所以在更新左右边界时，如果更新方式为: left = mid + 1 && right = mid 时，我们必须使用第一种求 mid 的方法: mid = left + (right - left) / 2，也就是偶数个元素时需要使用中间靠左的元素。

3、查找某个元素在nums出现的最后一个位置/找到小于等于key的最后一个元素位置

这种问题我们也称之为求右边界的问题，右边界位置的性质： 右边界以及左边的元素都是小于等于key的，而右边界右边的元素都是大于key的。

那么还是根据mid 的元素划分为两种情况：
(1) nums[mid] <= key ,此时说明 mid 位置以及左边都是小于等于key的，那么[0,mid]是一个合法区间，我们需要更新 left  = mid ，让[0,left]维护合法区间。注意不能更新为mid + 1；

(2) nums[mid] > key ，此时说明mid位置以及mid右边的元素都是大于key的，那么[mid,n-1]就是一个确定的不合法区间，我们需要更新 right = mid -1 。

在这种逻辑下，如果使用第一种求mid的方法，比如 left = 2 . right = 3，此时求出的mid = left ，而left一定是一个合法的位置，所以此时会更新 left = mid ，那么会陷入死循环。

也就是当更新边界逻辑为： left = mid && right = mid - 1 时，我们需要采取第二种求中间位置的做法 ： mid = left + (right - left + 1) / 2；

换一种更容易记忆的方式就是： 当left 更新的时候出现 + 1，那么求中间位置时不需要+1 ，反之如果left更新时没有出现+1，那么求中间位置时必须要+1。

1 二分查找

704. 二分查找 - 力扣（LeetCode）

本题就属于第一类基础的二分问题，我们直接套用模板就能解决。代码如下：

class Solution {
public:int search(vector<int>& nums, int key) {int left = 0, right = nums.size() - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] > key)right = mid - 1;else if (nums[mid] < key)left = mid + 1;else return mid;}return -1; }
};

2 在排序数组中查找元素的第一个和最后一个位置

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

题目解析：本题需要我们求出元素在有序数组中出现的第一个位置和最后一个位置。

第一个位置其实就是左边界，左边界左边的元素都是小于key的，而左边界以及右边的元素都是大于key的，那么直接使用左边界的模板来做。而最后一个位置其实就是右边界，右边界以及左边的的元素都是小于等于key的，而右边界右边的元素都是大于key的，直接使用右边界的模板来做。

细节：由于我们要求的是大于等于/小于等于key的左右边界，如果数组中根本没有key这个元素，那么其实就转换为了求 大于/小于key 的左右边界，也就是说找不到key第一次和最后一次出现的位置。

同时对于数组为空的特殊情况我们也需要特殊处理。

代码如下：

class Solution {
public:vector<int> searchRange(vector<int>& nums, int key) {if(nums.empty()) return {-1,-1};int left = 0 , right = nums.size() - 1 , res1 = -1 , res2 = -1 , mid;while(left < right){ //求边界问题时一定会有结果，所以循环结束条件为left和right相遇，也就是只剩一个合法元素，但是边界问题的边界位置并不一定就是我们所需的key，因为求的是大于等于或者小于等于，如果数组中根本没有出现key，那么边界位置的元素自然就不会是keymid = left + (right - left) / 2;if(nums[mid] >= key) right = mid; else left = mid + 1;}if(nums[left] == key) res1 = left;left = 0 , right = nums.size() - 1;while(left < right){mid = left + (right - left + 1) / 2;if(nums[mid] <= key) left = mid; else right = mid - 1;}if(nums[left] == key) res2 = left;return {res1 , res2};}
};

3 x 的平方根 

69. x 的平方根 - 力扣（LeetCode）

题目解析：题目要求我们求出x 的平方根，如果x的平方根是小数的话，那么省区小数部分，只保留整数部分。

换一种说法就是一个在[0,x]区间内找到一个值 res ， res 以及res左边的所有元素的平方都小于等于x，res右边的所有元素的平方都大于x，本质就是一个右边界的问题。

代码如下：

class Solution {
public:int mySqrt(int x) {long long left = 0 , right = x , mid; //使用long long 防止溢出while(left < right){mid = left + (right - left + 1) / 2;if(mid * mid > x) right = mid - 1; //>=mid的数都不是想要的结果else left = mid ; //结果在left和left右边，当然同时也 <= right}return left;}
};

4  搜索插入位置

35. 搜索插入位置 - 力扣（LeetCode）

题目解析：本题要求我们在有序数组中找某个值并返回下表，如果找不到，那么返回该值应该插入的位置下标，该值的插入下标其实就是大于该值的第一个位置。

那么综上，我们可以理解为找到第一个大于等于 key 的元素下标。其实就是一个左边界问题。

细节问题：key有可能大于nums所有元素，此时做二分查找也只能找到最后一个位置，而实际上需要插入的是最后一个位置的下一个位置，所以我们需要特殊处理一下。

代码如下：

class Solution {
public:int searchInsert(vector<int>& nums, int key) {//特殊情况： key 大于nums所有元素，那么插入到最后面if(key > nums.back()) return nums.size();int left = 0 , right = nums.size() - 1 , mid; while(left < right){mid = left + (right - left) / 2;if(nums[mid] < key) left = mid + 1;else right = mid;}return left;}
};

5 山脉数组的峰顶索引

852. 山脉数组的峰顶索引 - 力扣（LeetCode）

题目解析：给定一个山脉数组，也就是数组的前半部分上升，后半部分下将，让我们找到这个峰顶元素的下标。

暴力解法：遍历每一个元素，如果他的左边比他小且右边比他小，那么就是峰顶元素。

本题初看起来，数组并不是完全有序的，似乎无法使用二分来做，但是我们说过，并不是只有有序数组才能使用二分算法，而是只要具有二段性的数据，我们就可以使用二分算法，在本题中，二段性就是：以峰顶元素为分界点，左边的区间数据都是呈上升趋势，右边的区间数据都是呈下降趋势。那么我们可以定义一个位置i的趋势就是 i 和 i +1 位置的元素的大小关系。如果 nums[i] > nums[i+1] ，那么i是下降趋势，如果 nums[i] < nums[i+1] ，那么i呈上升趋势。

那么本题就转换为了求呈上升趋势的最后一个位置，也就是求右边界的问题。但是这样一来，我们求出的是峰顶元素的前一个位置，如果峰顶元素是第一个元素，那么无法求出答案，需要特殊判断一下。

那么我们可以换一种思路，就是求下降趋势的最左位置，转换成左边界问题，这样一来，求出的位置就是峰顶元素的位置，同时不需要担心峰顶元素在第一个位置。

代码如下：

class Solution {
public:int peakIndexInMountainArray(vector<int>& nums) {//转换为求下降趋势的最左位置int left = 0 , right = nums.size() - 2 , mid;  //我们认为最后一个点没有趋势，所以从倒数第二个位置来做while(left < right){mid = left + (right - left) / 2;if(nums[mid] < nums[mid + 1]) left = mid + 1;else right = mid;}return left;}
};

题目隐含了数据是递增和递减的，所以不会出现相等的情况。

6 寻找峰值

162. 寻找峰值 - 力扣（LeetCode）

题目解析：题目给定一个数组，要求我们返回任意一个峰值的下标。

暴力解法：遍历每一个点是否为峰值。

边界条件，我们可以将数组前面和后面看成负无穷，也就是第一个元素是上升过来的，最后一个元素会下降。

虽然本题存在多个峰值，但是并不影响二段性的成立。

我们还是定义i位置的趋势为 nums[i] 和 nums[i+1] 的关系。

在[left,right]区间中，mid有两种情况：

1、mid位置呈下降趋势，那么mid或者mid的左边一定有一个峰值，我们可以更新right = mid 。为什么这样说呢？等看完更新策略再论。

2、mid位置呈上升趋势时，mid右边一定存在一个峰值，此时可以更新left= mid + 1；

为什么 [left,mid] 或者 (mid,right] 区间内一定有一个峰值呢？

我们的初始情况 left = 0 , right = n - 1 ，此时区间左侧(left之前)是上升趋势，最右侧是下降趋势，那么区间内一定存在峰值，这一点毫无疑问。

在初始情况下，我们如果更新了 left = mid + 1，说明mid是上升趋势，那么left更新为 mid + 1，说明left之前也是上升趋势，而right是下降趋势，那么更新之后的[left,right] 也一定存在一个峰值。

如果更新的是 right =  mid ， 此时mid 是下降趋势，那么right也还是下降趋势，而left不管是初始情况还是经过一系列更新，left的左侧一定是上升趋势，那么[left,right]内一定有一个峰值。

我们还是当成左边界问题来求，找出下降趋势的最左边界。

本题由于数组外我们可以看成负无穷，所以0和n-1位置都有可能是峰值，初始化left和right 的时候需要注意。

代码如下：

class Solution {
public:int findPeakElement(vector<int>& nums) {int left = 0 , right = nums.size() - 1;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] < nums[mid + 1]) left = mid + 1;  //mid是上升趋势，那么mid右边一定存在峰值else right = mid ; //mid为下降趋势，那么mid或者mid左边一定存在一个峰值}return left;}
};

如果题目要我们找的是谷底元素的下标，那么其实就和求峰值是反着的，大体思路都是一样的。

7 寻找旋转排序数组中的最小值 

153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

题目解析：题目给定一个升序数组经过若干次旋转之后的数组，要我们求出数组的最小值。

暴力解法：遍历所有位置，找出所有都比自己小的位置。

本题我们如何发掘目标位置为分界的二段性呢？ 除了最小值的前一个元素是下降趋势，其他的位置都是上升趋势，我们如何理解呢？把数据看成一条斜线段的话，那么可以把旋转之后的线段用图表示出来：

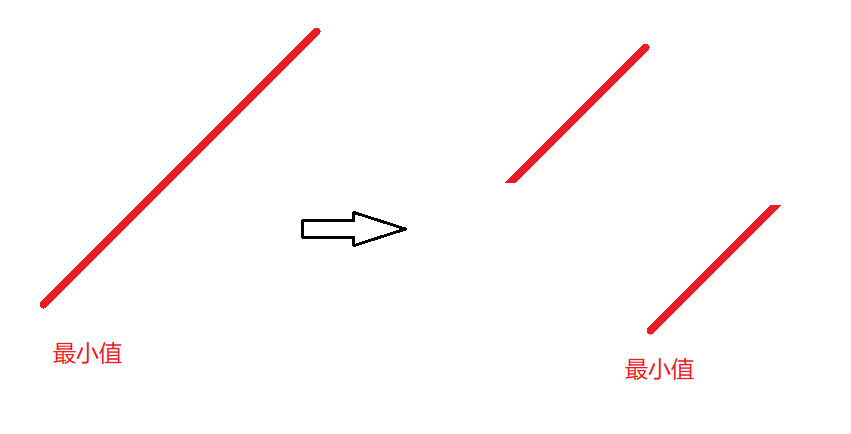
我们求出来的mid可能在两段线段中的任意一个位置：如果mid位置的元素大于nums[0] ，那么说明mid位置是在左边的线段上，那么最小值只会出现在 [mid+1 , right]。

如果mid位置的元素小于 nums[0] ，那么mid一定是位于右边的线段上，最小值只会出现在[left,mid]中。

那么我们只需要维护好left和right，让left一直在左边线段移动，但是left一直想要跳出左边线段，到达最小值的位置(left = mid + 1)，right一直在右边线段移动。

其实本题就相当于找到小于 nums[0] 的左边界位置。

本题的二段性就是：

最小值和右边的数据都小于 nums[0]  , 最小值左边的数据都大于等于 nums[0]。 

边界问题：如果最小值就位于最左侧，那么所有的值都是大于nums[0] 的，left会不断向移动直到最后一个元素。但是此时我们需要的是最左边的元素，所以当相遇位置在 n - 1 的时候，是有两种情况的，一种是最小值就是在最后一个位置，一种就是最小值在最左侧，我们取二者的较小值返回。

代码如下：

class Solution {
public:int findMin(vector<int>& nums) {int left = 0 , right = nums.size() - 1 , mid;while(left < right){mid = left + (right - left)  / 2;if(nums[mid] >= nums[0]) left = mid + 1;else right = mid;}return left == nums.size() - 1 ? min(nums[0] , nums.back()):nums[left];}
};

当然本题也可以和最右边的数比大小，甚至会比上面的代码更简单，不需要考虑left==n-1的特殊情况。

8 LCR 173. 点名

LCR 173. 点名 - 力扣（LeetCode）

题目解析：有n个学生学号为 0~n-1，按顺序点名，并将点到的学号按顺序记录在数组中，其中有一个同学缺席，我们需要找出缺席的学号。

暴力解法：遍历一遍看哪个位置元素与下标不同，那么学号为该下标的同学就缺席了。

本题的二段性：

[left,right] 区间内，求出mid，此时我们可以思考一下，[left,mid] 和 [mid,right] 这两个区间内如果都不缺席，应该有多少个学生？ 对于[left,mid] ，如果没有学生缺席的话，那么共有 nums[mid] - nums[left] + 1 个学生，而实际区间内只有 mid - left + 1个学生。

如果[left,mid] 区间内的应有学生数大于实际学生数，那么说明在学号 [left , mid] 之间一定有某个学号不在数组中。

反之如果[left,mid]区间内的应有学生数和实际学生数相等，那么说明在 [mid + 1, right] 的学号区间内有一个学生缺席了。 

其实在判断的时候，我们可以利用一下下标和值的关系来判断，如果 nums[mid]  == mid ，说明mid和之前的学生都在，那么 left = mid + 1；否则就说明在left或者left前面有学生缺席了。

特殊情况：缺席的是最后一个学生，那么此时数组里面其实展现出来的就是一个完全升序不缺失的数组，也就是一个 0 ~ n - 2 的升序排列，而循环结束时left只能停在 n - 2 ，如果返回n-2就会有问题。

如何解决这种特殊情况？ 很简单，如果缺失的是最后一个学生，那么此时最后一个位置的下标和里面存的值是一样的，也就是 nums[left] == left , 如果left也是到了最后一个位置，但是nums[left] == left + 1，说明最后一格同学在，缺席的是学号为  left 的同学。

代码如下：

class Solution {
public:int takeAttendance(vector<int>& records) {int mid , left = 0 , right = records.size() - 1; while(left < right){mid = left + (right - left) / 2;if(mid < records[mid]) right = mid;else left = mid + 1;}return left == records[left] ? left + 1 : left;}
};

总结

如果我们能够在数据中找到二段性，那么二分算法是一个非常非常快的算法，二分算法的核心并不是严格有序，而是数据的二段性。