leetcode700：二叉搜索树中的搜索(递归与迭代双解法)

LeetCode 700. 二叉搜索树中的搜索，【难度：简单；通过率：79.2%】，这道题是对 BST基本功的考察

一、 题目描述

给定二叉搜索树（BST）的根节点 root 和一个整数值 val

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。如果节点不存在，则返回 null

示例:

示例 1:

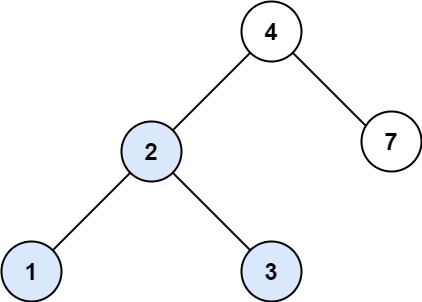
输入: root = [4,2,7,1,3], val = 2
输出: [2,1,3]

示例 2:

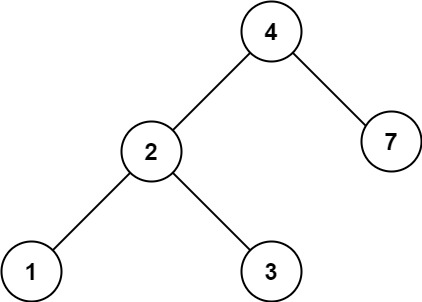
输入: root = [4,2,7,1,3], val = 5
输出: []

---

二、 核心思路：利用 BST 的有序性

二叉搜索树最关键的性质就是它的有序性：

• 对于任意节点，其左子树中所有节点的值都小于该节点的值
• 其右子树中所有节点的值都大于该节点的值

这个性质使得我们查找时，在每个节点都可以做出明确的决策，从而避免了对整棵树的盲目遍历。查找过程就像是在走一个决策路径：

1. 从根节点 root 开始
2. 如果当前节点的值等于 val，那么就找到了，返回当前节点
3. 如果 val 小于当前节点的值，那么目标只可能在左子树中，我们向左走
4. 如果 val 大于当前节点的值，那么目标只可能在右子树中，我们向右走
5. 如果走到了 null，说明树中不存在值为 val 的节点，返回 null

---

解法一：递归 (最佳实践)

递归是实现 BST 查找最自然的方式，代码可以写得非常简洁和优雅

代码实现

class Solution {public TreeNode searchBST(TreeNode root, int val) {// 1. 递归终止条件：// root 为 null，说明没找到，返回 null// root.val == val，说明找到了，返回当前 root 节点if (root == null || root.val == val) {return root;}// 2. 根据 val 和 root.val 的大小关系，决定去哪个子树继续搜索// 并直接返回子树搜索的结果if (val < root.val) {return searchBST(root.left, val);} else {return searchBST(root.right, val);}// 上面的 if-else 也可以写成一个更简洁的三元表达式：// return val < root.val ? searchBST(root.left, val) : searchBST(root.right, val);}
}

深度解析

• 优雅的终止条件：if (root == null || root.val == val) 这一行代码，将**“没找到”和“找到了”**这两种递归的终点情况完美地结合在了一起
• 直接返回：return searchBST(...) 是递归思想的精髓。当前函数不需要关心子问题是如何解决的，它只需要将子问题的解（找到的节点或 null）直接作为自己的解返回给上一层

---

解法二：迭代 (另一种最佳实践)

虽然递归很优雅，但在某些场景下（如树非常深导致栈溢出），迭代是更稳健的选择。迭代解法不使用递归栈，空间复杂度为 O(1)

核心思路

使用一个指针 node，从 root 开始，根据 val 和 node.val 的大小关系，不断地将指针移向左子树或右子树，直到找到目标或指针变为 null

代码实现

class Solution {public TreeNode searchBST(TreeNode root, int val) {TreeNode node = root; // 使用一个指针进行遍历// 当节点不为空时，循环继续while (node != null) {if (val == node.val) {// 找到了，返回当前节点return node;} else if (val < node.val) {// 目标值更小，去左子树node = node.left;} else {// 目标值更大，去右子树node = node.right;}}// 循环结束（node 变为 null），说明没找到return null;}
}

深度解析

• O(1) 空间：整个过程只用了一个额外的指针 node，空间开销是常数级的
• 循环代替递归：while 循环完美地替代了递归的调用过程，逻辑清晰，易于理解

---

四、 复杂度分析与总结

	解法一 (递归)	解法二 (迭代)
时间复杂度	O(H)，其中 H 是树的高度。最坏情况下（树退化为链表）为 O(N)	O(H)，其中 H 是树的高度。最坏情况下（树退化为链表）为 O(N)
空间复杂度	O(H) (递归栈的开销)。最坏情况下为 O(N)	O(1) (只使用了常数个额外指针)
代码可读性	高，与问题的递归定义高度匹配	高，循环逻辑清晰
适用场景	大多数情况，代码简洁	树非常深，或对栈空间有严格限制的场景