当前位置：首页 > news >正文

Python-深度学习--1交叉熵损失函数

news 2025/8/11 5:41:56

交叉熵损失函数（Cross-Entropy Loss）是机器学习和深度学习中用于分类任务的核心损失函数，尤其适用于解决多类别分类问题。它通过衡量模型预测概率分布与真实标签分布之间的 “差异”，指导模型参数优化，最终让预测结果更接近真实情况。

一、核心原理：衡量概率分布的差异

交叉熵（Cross-Entropy）原本是信息论中的概念，用于量化两个概率分布之间的 “不相似程度”。在机器学习中：

假设模型对样本的预测结果是一个概率分布（例如，对 “猫 / 狗 / 鸟” 三分类，预测为猫的概率 0.8、狗 0.1、鸟 0.1）；
样本的真实标签也是一个概率分布（例如，真实是猫，则分布为 [1, 0, 0]，即 “独热编码”）；
交叉熵损失函数计算这两个分布的差异，差异越大，损失值越高；差异越小，损失值越低。

二、数学定义

1. 二分类场景（输出为 0 或 1）

对于二分类问题（如 “垃圾邮件识别”“疾病诊断”），模型通常通过sigmoid函数输出单个概率值（属于类别 1 的概率），交叉熵损失公式为：

L=−y⋅log(y^)−(1−y)⋅log(1−y^)

其中：

y 是真实标签（0 或 1）；
y^ 是模型预测的概率（0~1 之间）；
log 是自然对数。

示例：
若真实标签 y=1，模型预测 y^=0.9，则损失 L=−1⋅log(0.9)−0⋅log(0.1)≈0.105（损失小，预测准确）；
若模型预测 y^=0.1，则损失 L=−1⋅log(0.1)≈2.303（损失大，预测错误）。

2. 多分类场景（输出为多个类别）

对于多分类问题（如 “手写数字识别”“图像分类”），模型通过softmax函数输出每个类别的概率（所有类别概率和为 1），交叉熵损失公式为：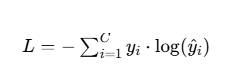

其中：

C 是类别总数；
yi 是真实标签的第i个值（独热编码，只有真实类别为 1，其余为 0）；
y^i 是模型预测第i类的概率。

示例：
3 分类问题中，真实标签 y=[1,0,0]（属于第 1 类），模型预测 y^=[0.8,0.1,0.1]，则损失 L=−1⋅log(0.8)−0⋅log(0.1)−0⋅log(0.1)≈0.223（预测准确，损失小）；
若模型预测 y^=[0.1,0.8,0.1]，则损失 L=−1⋅log(0.1)≈2.303（预测错误，损失大）。

三、为什么用交叉熵损失？

与概率天然契合：分类任务的输出本质是 “属于每个类别的概率”，交叉熵直接衡量概率分布的差异，物理意义明确。
梯度特性更优：相比平方损失（MSE），交叉熵在模型预测错误时（如预测概率接近 0 但真实标签为 1），会产生更大的梯度，加速模型参数更新（收敛更快）。
- 例如，用平方损失时，当 y^=0.1 而 y=1，梯度为 −(y−y^)=−0.9；
- 用交叉熵时，梯度为 −y^y=−0.11=−10，更新幅度更大。
适配概率输出函数：与sigmoid（二分类）、softmax（多分类）函数配合时，导数计算更简洁，避免梯度消失问题。

四、代码实现（PyTorch 示例）

1. 二分类交叉熵（BCEWithLogitsLoss）

PyTorch 将sigmoid和交叉熵合并为BCEWithLogitsLoss，直接输入未经过sigmoid的原始输出（logits）：

2. 多分类交叉熵（CrossEntropyLoss）

PyTorch 的CrossEntropyLoss内置softmax，直接输入 logits，标签用类别索引（无需独热编码）：

代码如下：

import torch
import torch.nn as nn# 模型输出（未经过sigmoid，形状：[batch_size, 1]）
logits = torch.tensor([[2.0], [0.5], [-1.0]])  # 假设3个样本
# 真实标签（0或1，形状：[batch_size, 1]）
labels = torch.tensor([[1.0], [1.0], [0.0]])# 定义二分类交叉熵损失
criterion = nn.BCEWithLogitsLoss()
loss = criterion(logits, labels)
print(loss.item())  # 输出损失值（约0.412）#--------------------------------------------------------------------------
# 模型输出（未经过softmax，形状：[batch_size, num_classes]）
logits = torch.tensor([[3.0, 1.0, 0.2],  # 3个类别，2个样本[0.5, 2.0, 0.3]])
# 真实标签（类别索引，形状：[batch_size]）
labels = torch.tensor([0, 1])  # 第1个样本属于类0，第2个属于类1# 定义多分类交叉熵损失
criterion = nn.CrossEntropyLoss()
loss = criterion(logits, labels)
print(loss.item())  # 输出损失值（约0.326）

运行结果：