线段树学习笔记 - 区间最值操作

1. 前言

线段树系列文章：

• 线段树学习笔记。
• 线段树学习笔记 - 练习题（1）。
• 线段树学习笔记 - 练习题（2）。
• 线段树学习笔记 - 练习题（3）。
• 线段树学习笔记 - 动态开点线段树。

上一篇文章学习了这个视频的动态开点线段树，这篇文章来继续学习，学习视频：算法讲解114【扩展】线段树专题5-开点线段树、区间最值和历史最值，题目都是左神视频上的，思路也是学习的这个视频。

2. 维护区间最值问题

2.1 线段树结构

假设现在有一道题目，需要支持下面几种操作：

1. 0 l r x：将 arr[l] 到 arr[r] 这个范围的每个数字 v 更新为 min(v，x)
2. 1 l r：查询 arr[l] 到 arr[r] 的最大值
3. 2 l r：查询 arr[l] 到 arr[r] 的累加和

上面 2 和 3 就是范围最大值和范围累加和查询，这个可以用 max 数组和 sum 数组完成，但是第一种操作就比较麻烦了，比如原数组是 [1, 2, 3, 4, 5]，下标从 1 开始，然后现在要将 [1, 5] 范围的下标更新为 min(nums[i], 3)，更新之后的结果是 [1, 2, 3, 3, 3]。

为了解决这个问题，这里引入一个 sem 数组维护严格次大值，全部数组如下：

• arr：原始数组。
• sum：维护范围累加和。
• max：维护范围最大值。
• cnt：区间最大值个数，和上面 max 配合使用。
• sem：区间严格次大值（second max）

下面来看下什么是区间严格次大值，假设现在 [l，r，i] 对应的数组是 [1，4，4，4，5，5]，那么 max[i] = 5，cnt[i] = 2，sem[i] = 4，最大值是 5，严格次大值就是比 5 小的第二大的数。

假设现在 [l，r，i] 对应的数组是 [4，4，4，4，4，4]，那么 max[i] = 4，cnt[i] = 6，sem[i] = Integer.MIN_VALUE，最大值是 4，严格次大值就是比 4 小的第二大的数，没找到，就设置为 Integer.MIN_VALUE，当然这个严格次大值可以设置为数组的最小值，比如数组范围是 [-10000，10000]，那么次大值的默认值可以设置为 -10001。

下面再来看下 max 和 sem 是如何更新的。

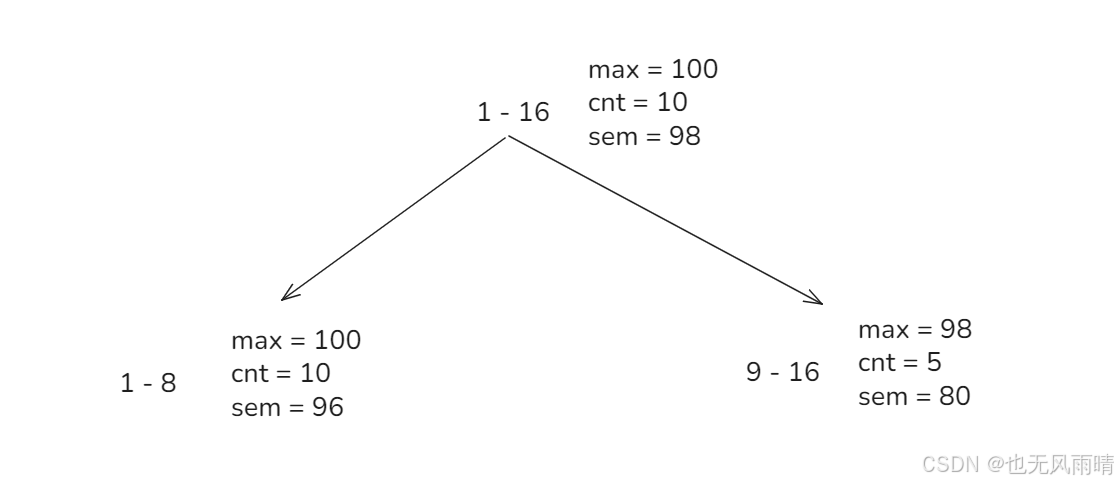
首先来看上面的图，这里只画出了三个节点，剩下的节点就省略了，主要还是先看下要怎么更新，假设现在的操作是 0 1 16 x，来到 1 - 16 这个节点，这里要遵循两个规则：

1. 如果更新的 x 比 max 大，那么就不管了，因为整个范围最大值就是 max，如果现在要更新的值 x > max，那就没必要更新。
2. 如果更新的 x > sem && x < max，那么懒更新当前节点的 max 和 sum，上面图没有画出 sum，但是更新也比较简单，max 就更新为 x，然后 sum 更新为 (max - x) * cnt
3. 如果更新的 x 比 sem 小，那么往左节点走，同时将当前节点攒着的 max 给下发下去。

就以上面为例子，比如现在假设 sum[i << 1] = 1096，sum[i << 1 | 1] = 570，然后 x 为 99，那么此时由于 max(98) > 99 > sem(98)，直接更新 sum[i] = 1066 - 10 * (99 - 98) = 1056，max = 99。

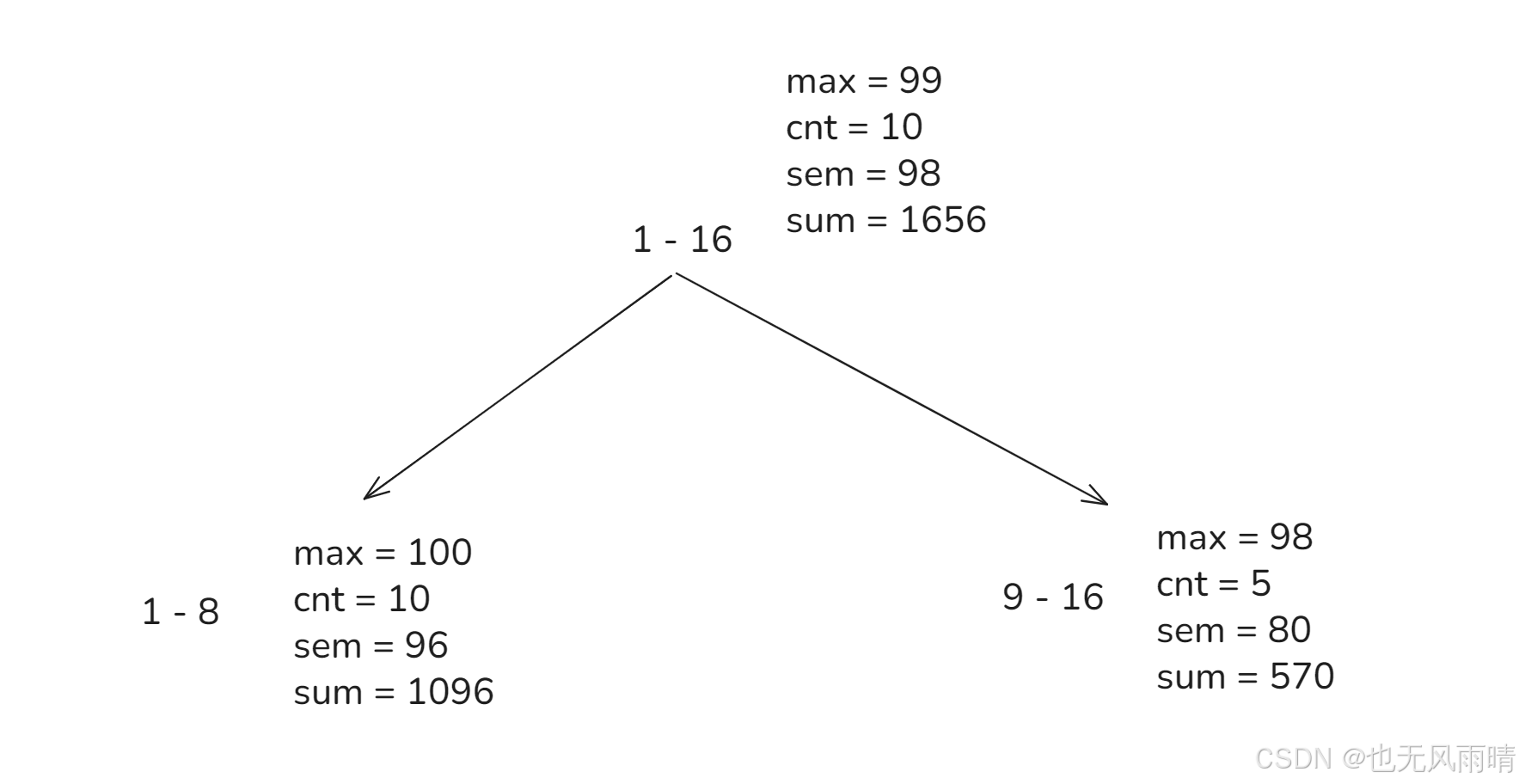
比如这时候要将 1- 16 范围更新为 97，那么这时候发现 97 < sem(98)，这时候将当前节点的 max 下发到左和右，由于 max = 99，下发到右节点的时候发现 99 < 98，所以右节点的值不变，左节点 max 修改为 99，然后 sum 修改为 1096 - (100 - 99) * 10 = 1086。

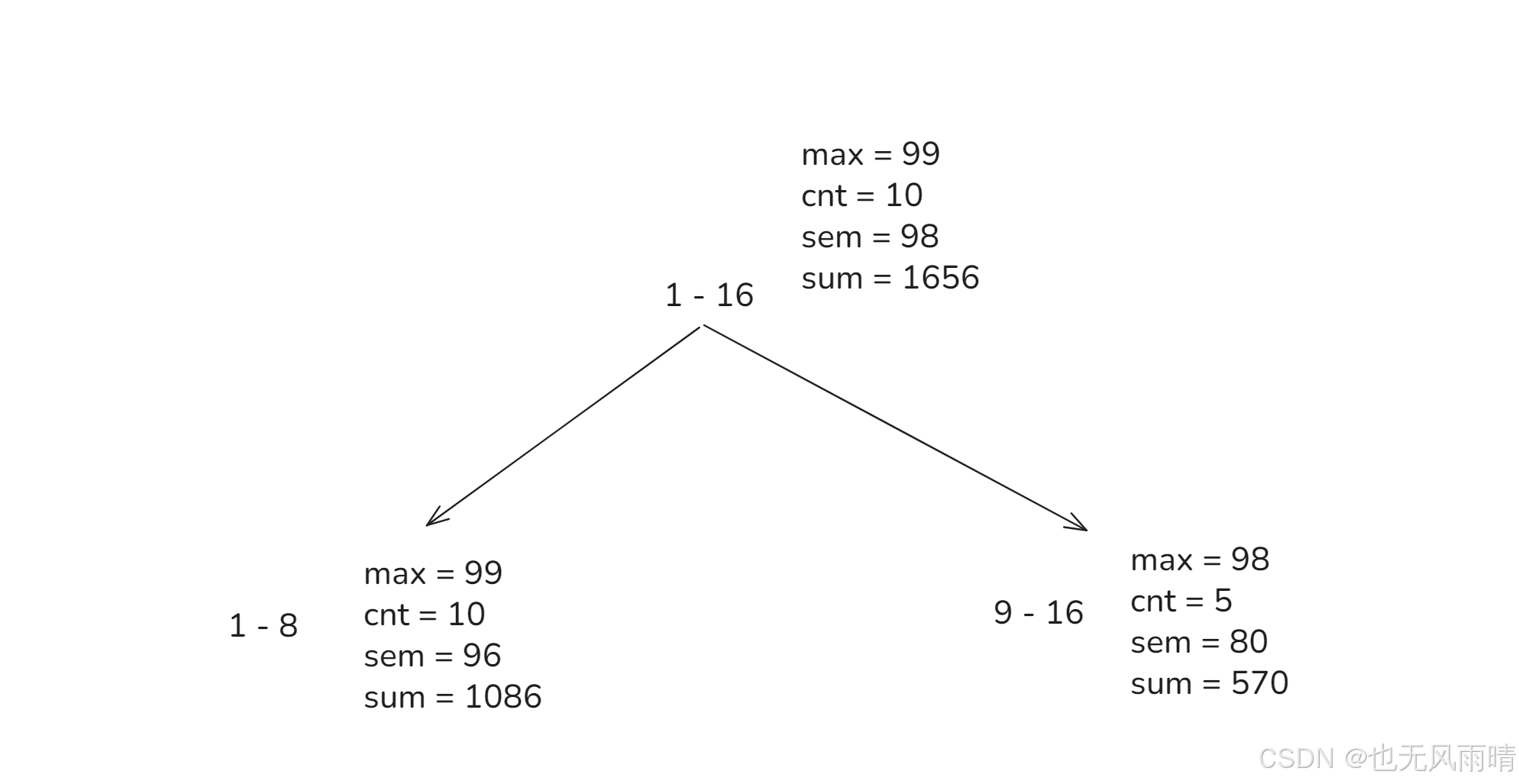
上面懒更新下发完了之后，这时继续往两边遍历，也就是 1-8 和 9-16。

• 来到 1 - 8 的时候发现 sem = 96 < 97 < max = 99，这时候符合规则 2，直接懒更新当前节点 max = 97，然后 sum = 1086 - (99 - 97) * 10 = 1066，更新完成。
• 来到 9 - 16 的时候发现 sem = 80 < 97 < max = 98，这时候符合规则 2，直接懒更新当前节点 max = 97，然后 sum = 570 - (98 - 97) * 5 = 565，更新完成。
• 返回 1 - 16，汇总左右节点，max = Math.max(97，97) = 97，cnt = 10 + 5 = 15，sum = 1066 + 565 = 1631。

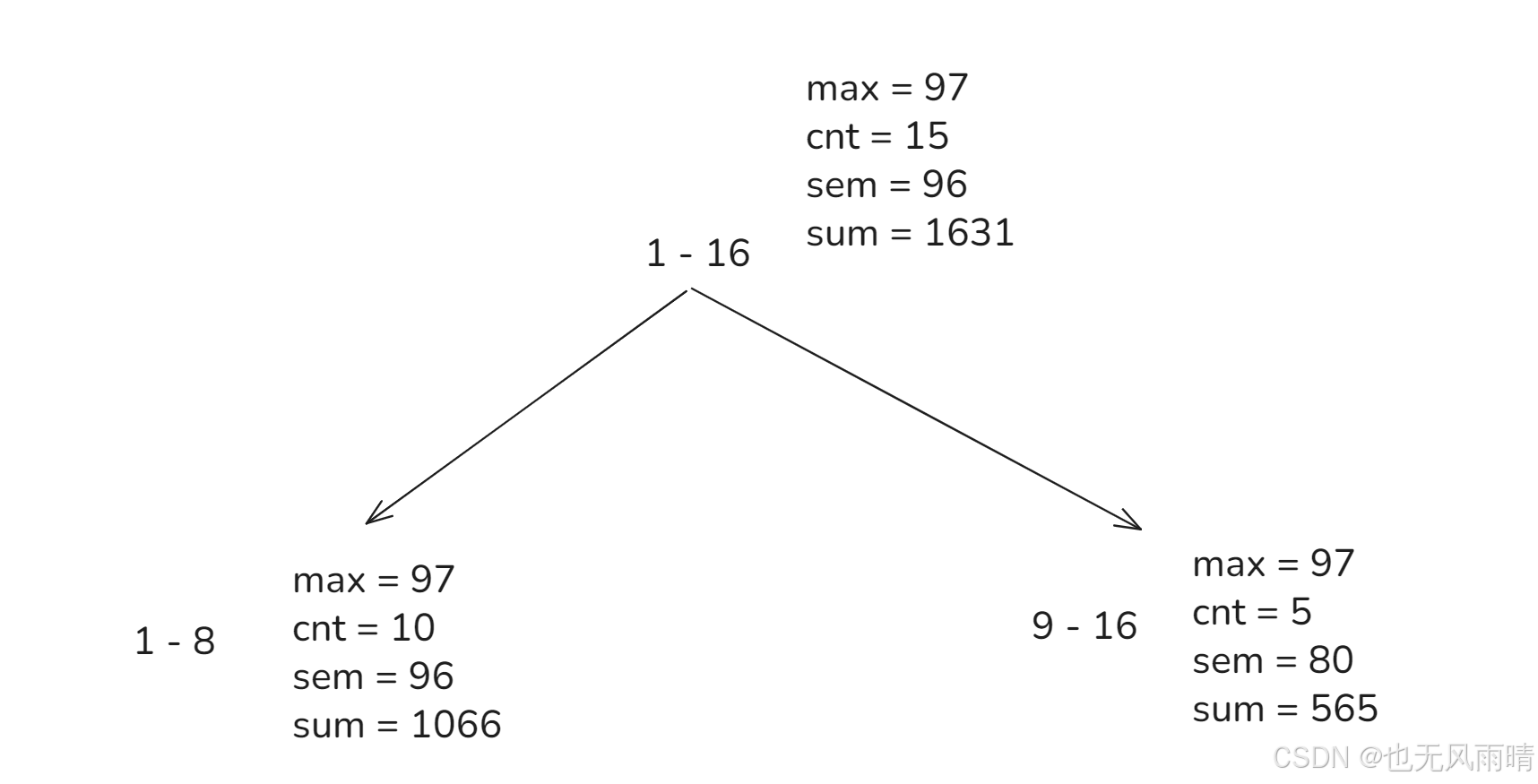
2.2 势能分析时间复杂度

下面来进行下势能分析，来看看整体时间复杂度，首先初始化一棵树，例子也是用视频里面的。

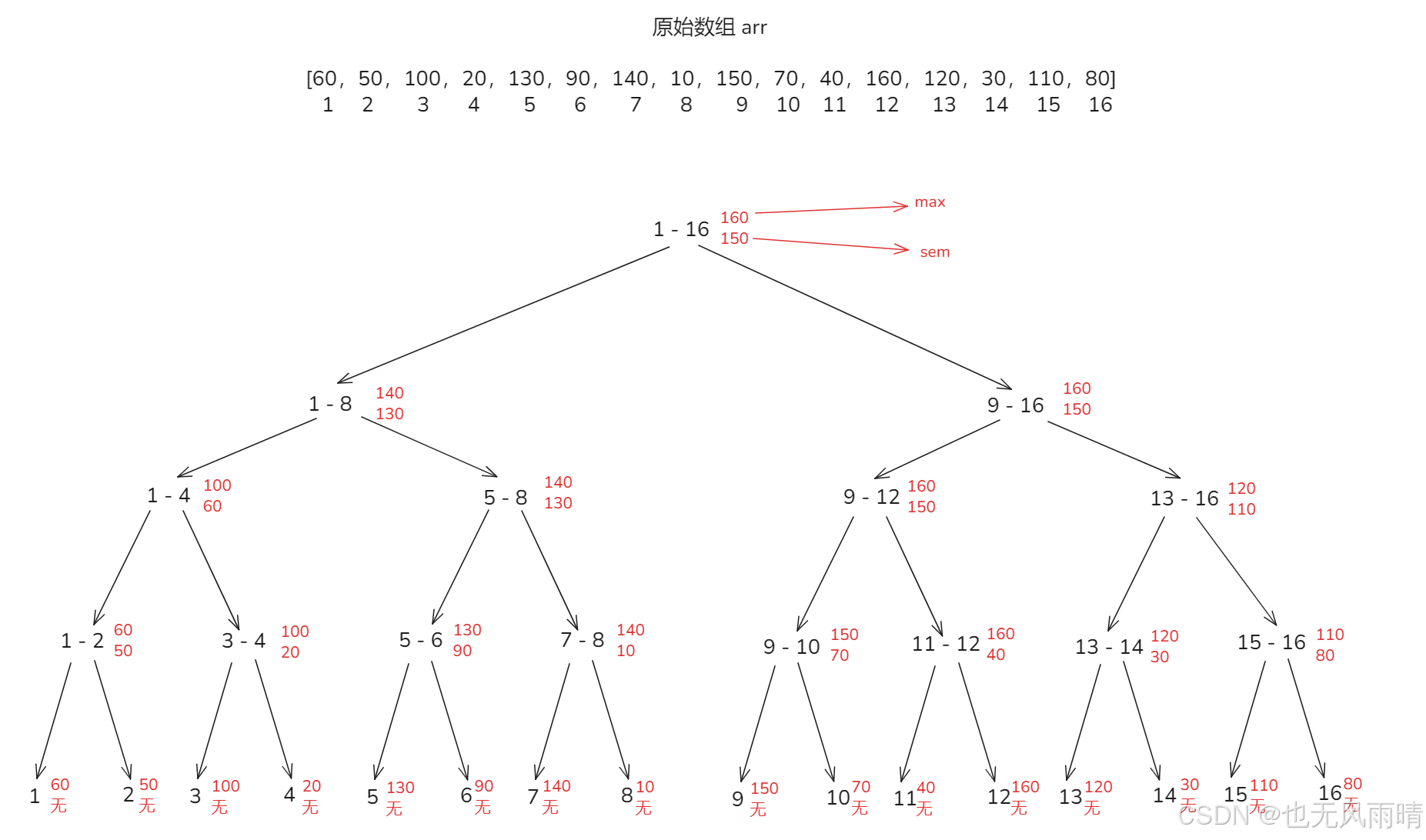
来看下上面的例子，定义了原数组为 [60，50，100，20，130，90，140，10，150，70，40，160，120，30，110，80]，构建出一棵线段树，上面只写出了 max 和 sem，因为更新最大值这件事向不向下传递看的是 max 和 sem，跟 sum 没有关系，而且 sum 更新也可以在 O(1) 时间内完成更新，所以这里就不看 sum 了。然后下面来做第一个操作，打标签，假设当前节点的最大值和父结点的最大值不一样，那么就给当前节点打个标签，至于这个标签有什么用，后面会用到。

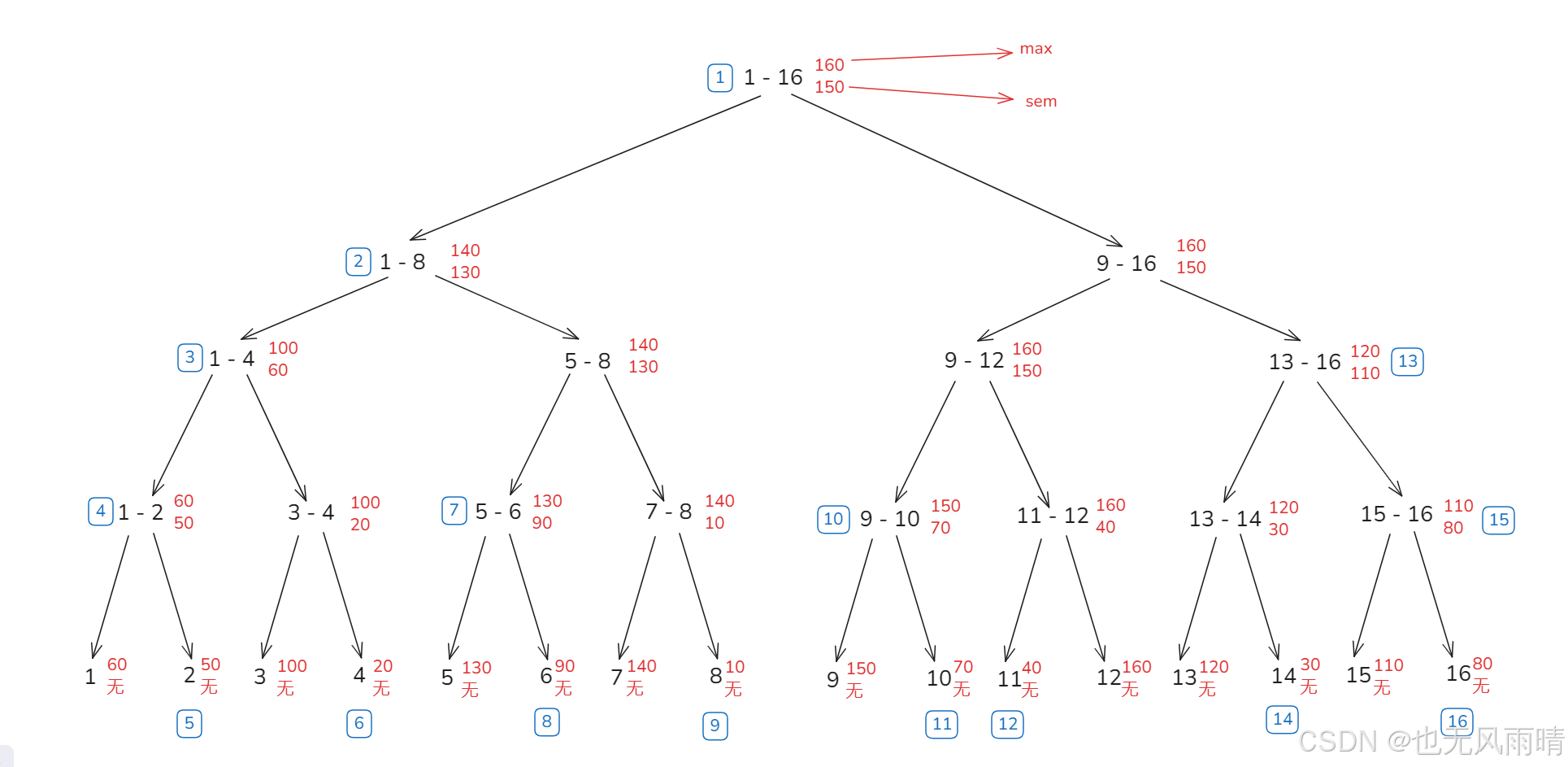
打上标签之后开始分析，首先标签的个数是 O(n) 的数量，线段树原始数组 O(n)，线段树最大数组长度也不会超过 4 * n，所以直接当 O(n) 的个数。

下面来左更新操作，将 1 - 16 范围的数字最大值更新为 75，更新之后的线段树变成了这样。

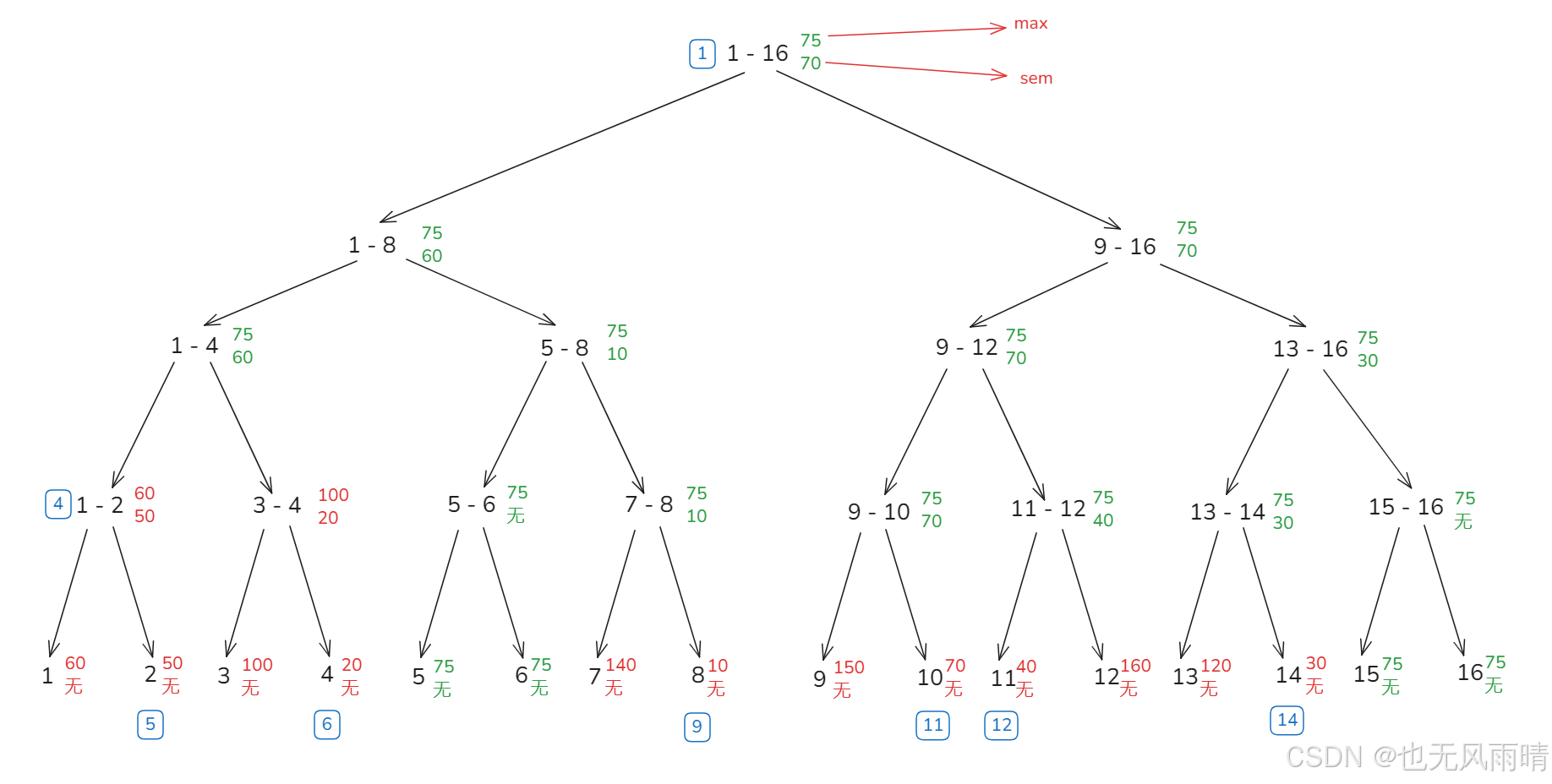
下面是遍历过程：

• 首先是 1 - 16 节点，因为 sem = 150 > 75，需要下发到左右节点。
• 来到 1 - 8 节点，因为 sem = 130 > 75，需要下发到左右节点
• 来到 1 - 4 节点，因为 sem = 60 < 75 < max = 100，直接在当前节点维护，设置 max = 75，sem 不变
• 来到 5 - 8 节点，因为 sem = 130 > 75，需要下发到左右节点
• 来到 5 - 6 节点，因为 sem = 90 > 75，需要下发到左右节点
• 来到 5 - 5 节点，因为 sem 不存在，因此直接修改最大值为 75，返回
• 来到 6 - 6 节点，因为 sem 不存在，因此直接修改最大值为 75，返回
• 回到 5 - 6 节点，通过左右节点维护当前节点的最大值和次大值，最大值是 75，次大值是 无
• 来到 7 - 8 节点，因为 sem = 10 < 75 < max = 140，直接修改最大值为 75，返回 5 - 8
• 回到 5 - 8 节点，通过左右节点维护最大值为 75，次大值为 10
• 回到 1 - 8 节点，通过左右节点维护最大值为 75，次大值为 60
• 来到 9 - 16 节点，因为 sem = 150 > 75，需要下发到左右节点
• 来到 9 - 12 节点，因为 sem = 150 > 75，需要下发到左右节点
• 来到 9 - 10 节点，因为 sem = 70 < 75 < max = 150，直接修改最大值为 75
• 来到 11 - 12 节点，因为 sem = 40 < 75 < max = 160，直接修改最大值为 75
• 回到 9 - 12 节点，通过左右节点维护最大值为 75，次大值为 70
• 来到 13 - 16 节点，因为 sem = 110 > 75，需要下发到左右节点
• 来到 13 - 14 节点，因为 sem = 30 < 75 < max = 120，直接修改最大值为 75
• 来到 15 - 16 节点，因为 sem = 80 > 75，需要下发到左右节点
• 来到 15 - 15 节点，因为 sem 不存在，因此直接修改最大值为 75，返回
• 来到 16 - 16 节点，因为 sem 不存在，因此直接修改最大值为 75，返回
• 回到 15 - 16 节点，通过左右节点维护最大值为 75，次大值为 无
• 回到 13 - 16 节点，通过左右节点维护最大值为 75，次大值为 30
• 回到 9 - 16 节点，通过左右节点维护最大值为 75，次大值为 70
• 回到 1 - 16 节点，通过左右节点维护最大值为 75，次大值为 70

上面就是详细流程，看起来是比较简单的，就是来到一个节点遇到 sem 如果小于设置的 value，就向左右两边下发，注意上面这里由于是第一次设置，每一个节点上都没有攒着什么懒更新信息，所以不会把懒更新下发。但是比如像上面的 1 - 4 节点现在最大值是 75，那么当后面要查询也好要设置最大值也好，遍历到这个节点要继续向左右节点遍历的时候就要把这个 max 懒下发到左右节点，也就是更新左右节点的最大值，之后再去遍历左右节点。所以说这里的 max 不单单作为一个最大值的维护信息，同时也作为了懒信息，前面的线段树维护最大值都说的是范围添加或者范围修改维护最大值，也就是 max 数组是单单作为一个最大值信息的，但是这里 max 不单单作为最大值，同时也作为了懒更新的信息。

然后再来看，经过上面的遍历，绿色的节点就是被修改过的，然后经过的节点如果有 标签 的就去掉，比如 5 - 6 这个节点原来有标签的，现在遍历修改过了，就把标签去掉，那么这个标签去掉有什么用呢？

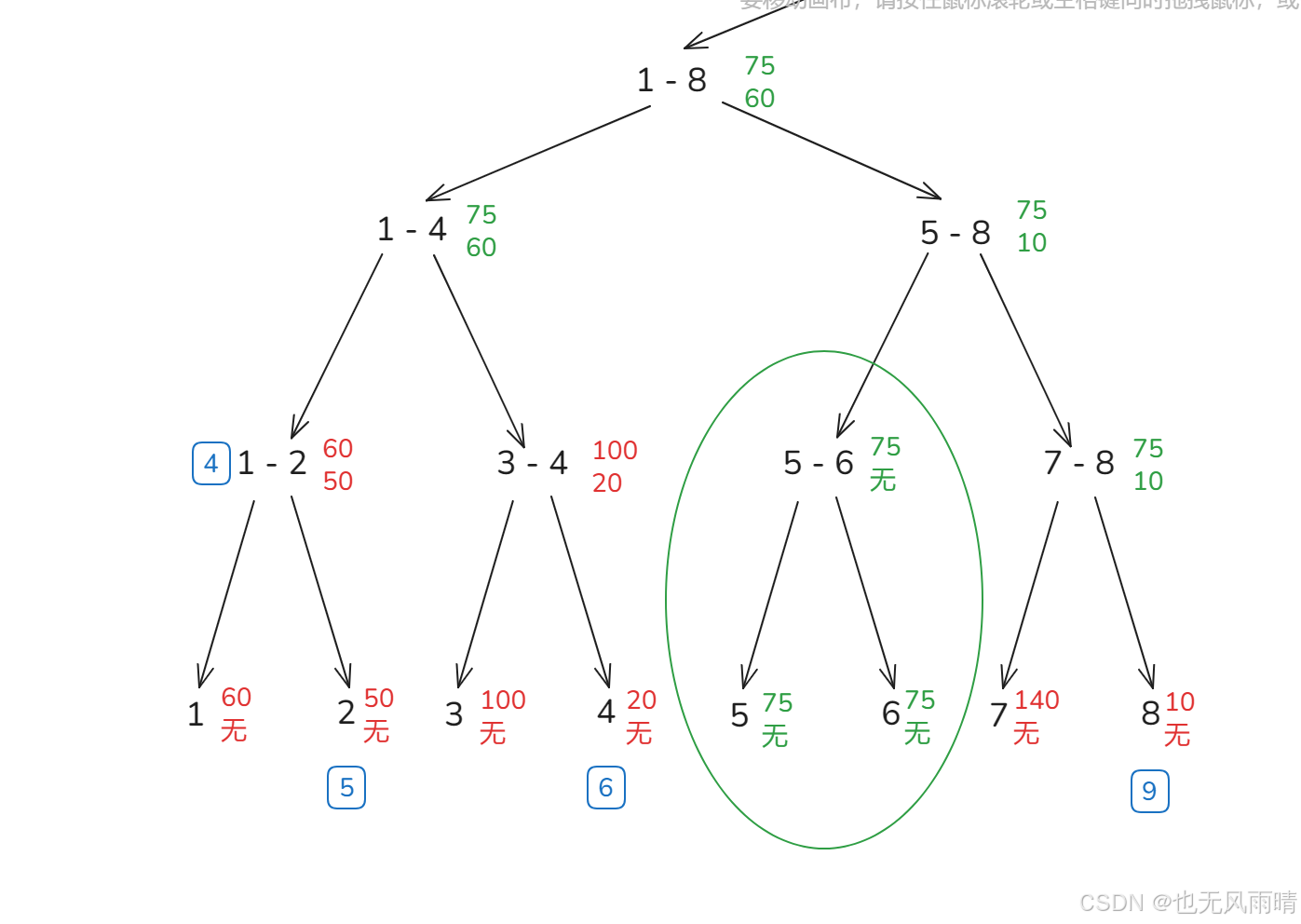
还是一样以 5 - 6 这个节点为例，当一棵子树没有任何的标签，就说明这棵子树统一了，上面 5 - 6 这棵子树所有的节点最大值和次大值都是一样的，那么此后但凡有修改动作，这棵子树都只是需要修改根节点就够了，非根节点不会再去遍历修改。比如现在我要修改最大值为 60，那么遍历到 5 - 6 的时候直接修改 5 - 6 这个节点的最大值为 60，然后就返回了，因为次大值是一定小于要修改的值的，因此完全不需要再往左右去遍历。

然后下面再来看下，将 1 - 16 范围修改最大值为 18，修改后的结果如下。

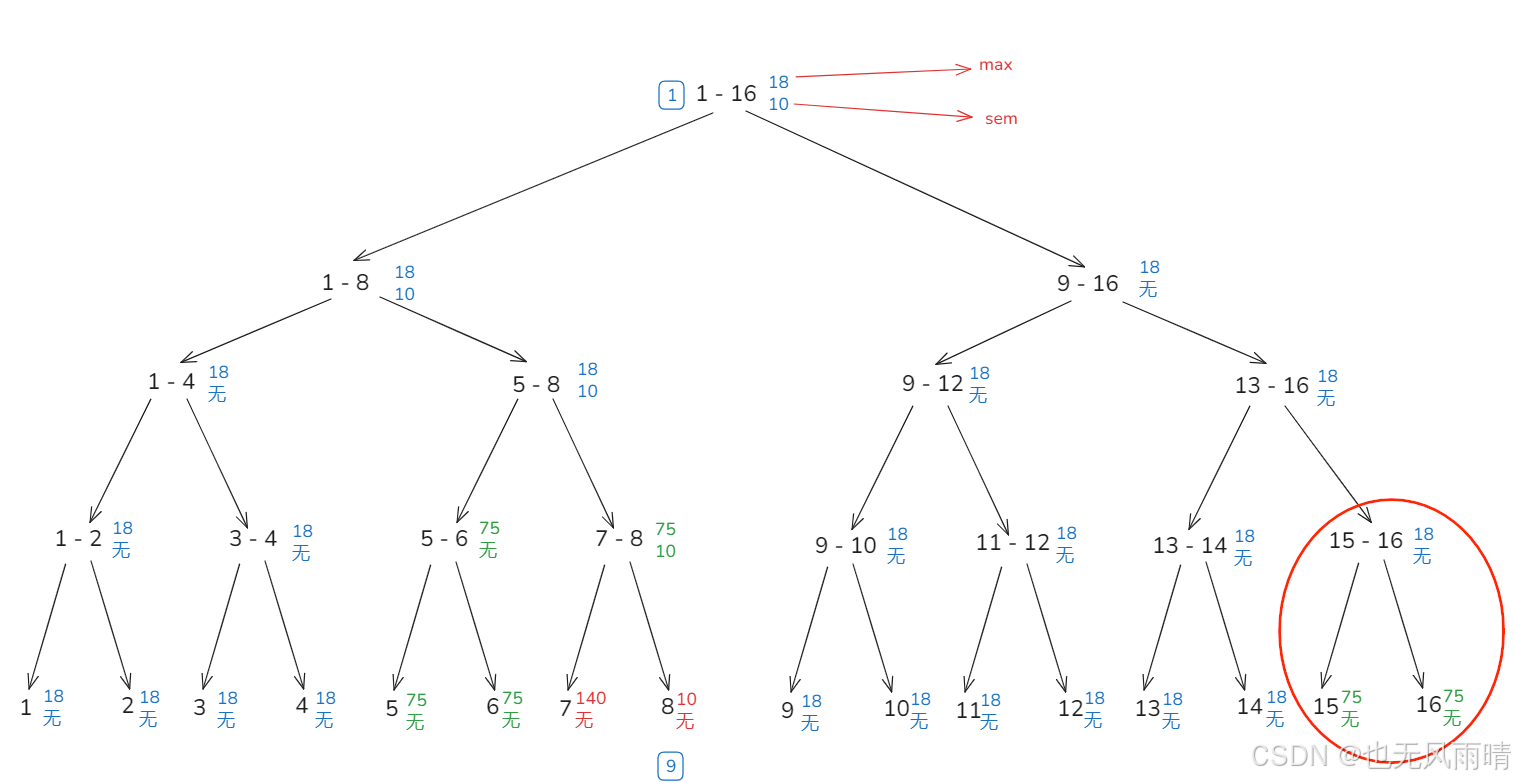
上面就是修改后的结果了，当然过程就不写出来了，可以看到上面红色部分，作为一个整体只需要修改根节点最大值即可返回，然后遍历的过程来到的节点标签都给回收掉，现在就只剩下一个标签了，最后一次更新，我们更新最大值为 5。

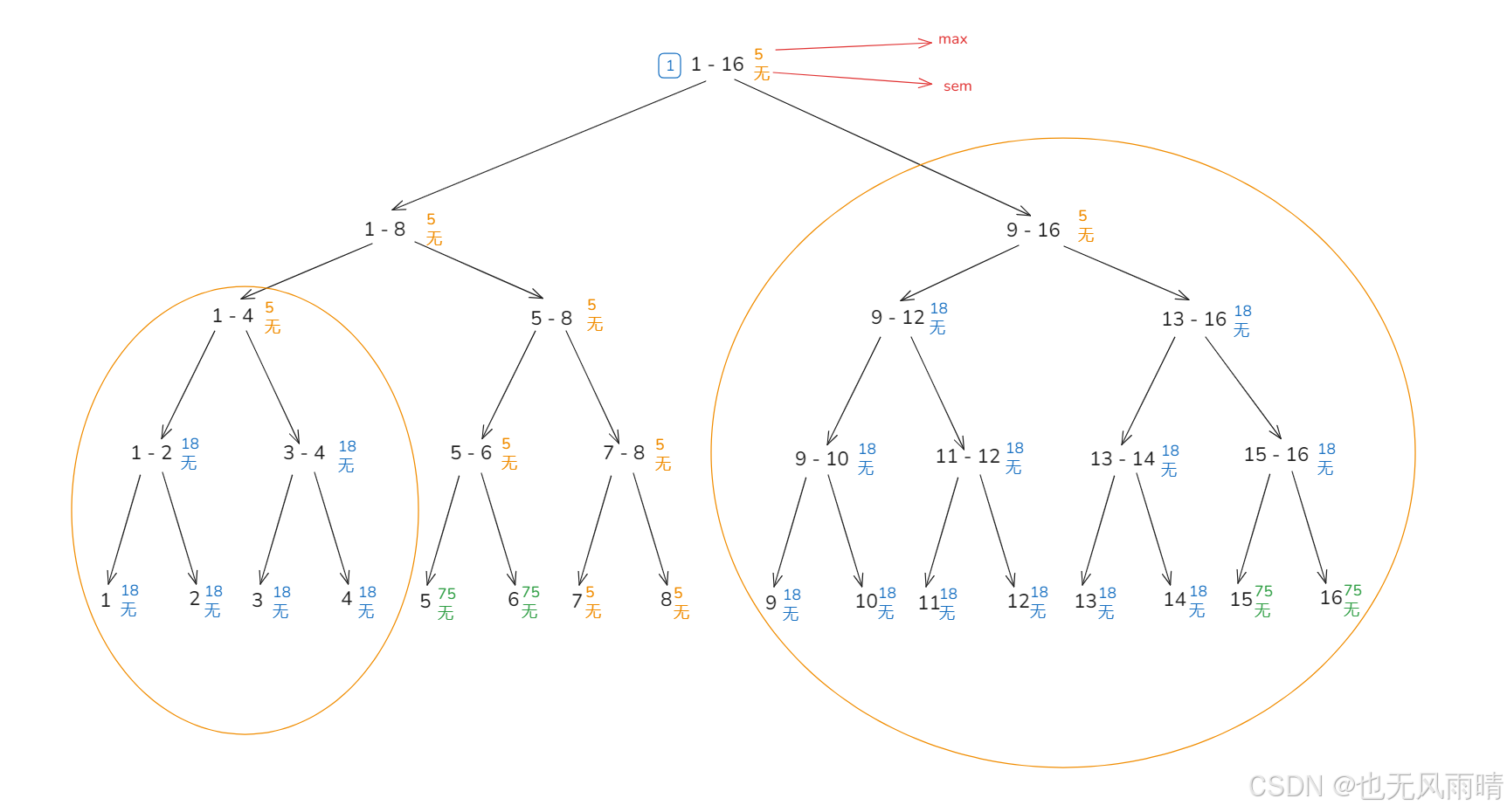
更新完之后，所有的标签都已经被回收，本次更新由于上面两个黄色圈的部分没有了标签，可以看成一个整体，因此只需要更新对应的根节点，根本不需要下发。

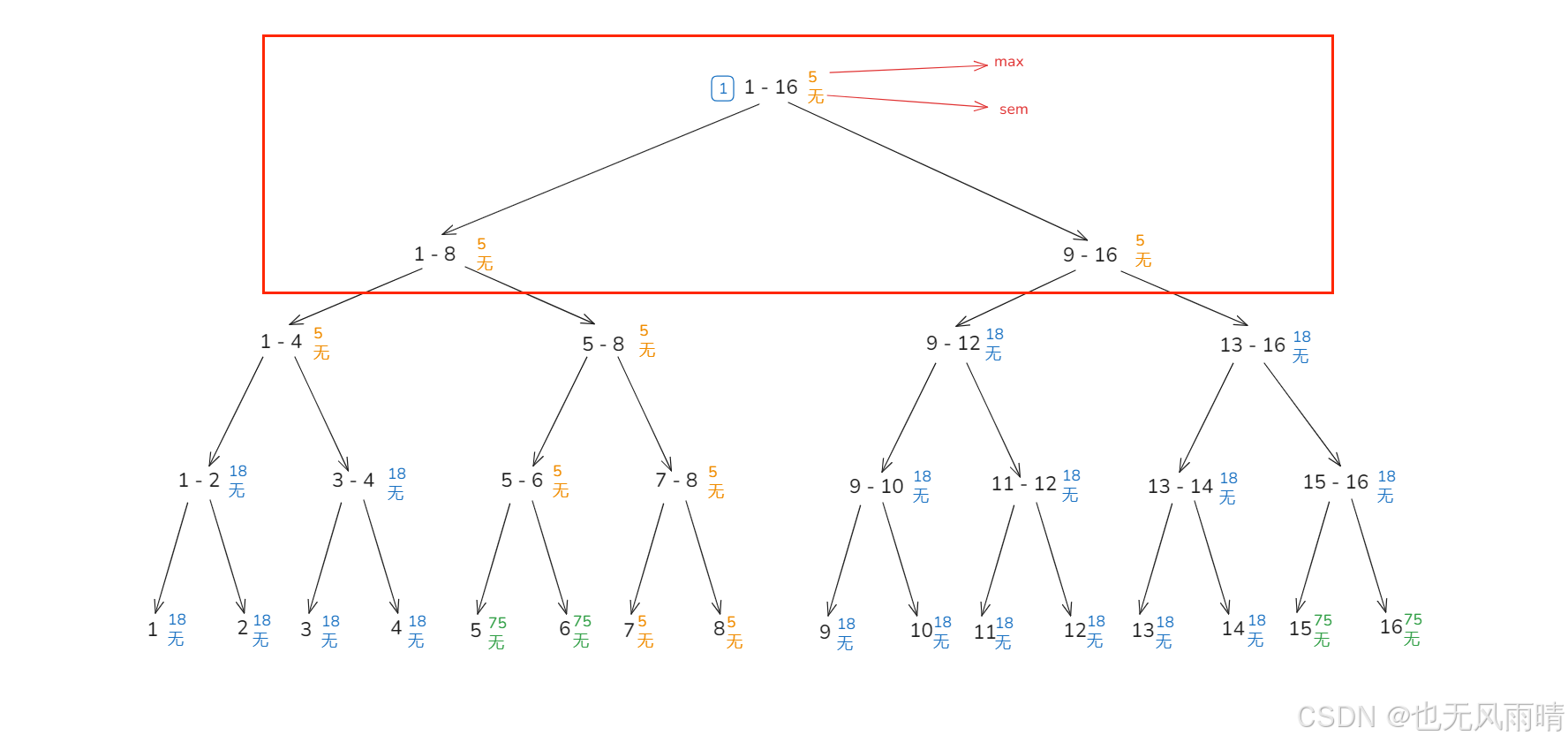
到现在，根节点 1 - 16 和两个子节点的最大值和次大值都一样了，且标签全部被回收，以后再有更新最大值的请求过来，只需要更新 1 - 16 这个节点即可，时间复杂度为 O(1)。

到这里就遍历完了，可以发现，由于这里线段树超过 4 * n 的规模，所以标签数空间也是 O(n) 的规模，那么回收一个标签需要从根节点经过 $lo{g}_{2}n$ 的高度，因此整体的时间复杂度是 $n\ast lo{g}_{2}n$。

2.3 代码

这里主要来看 up 的方法，就是如何根据两个子节点来更新出父结点的 sem、max、sum 数组。

private static void up(int i) {int l = i << 1;int r = i << 1 | 1;// 左 + 右sum[i] = sum[l] + sum[r];// 左和右的最大值比较max[i] = Math.max(max[l], max[r]);// 如果最大值来自左边if (max[l] > max[r]) {// 父结点的最大值个数就跟左边一样cnt[i] = cnt[l];// 次大值就从左边的次大值和右边的最大值里面选出sem[i] = Math.max(sem[l], max[r]);// 如果最大值来自右边} else if (max[l] < max[r]) {// 父结点的最大值个数就跟右边一样cnt[i] = cnt[r];// 次大值就从左边的最大值和右边的次大值里面选出sem[i] = Math.max(max[l], sem[r]);} else {// 父结点的最大值个数就是左节点最大值个数 + 右节点最大值个数cnt[i] = cnt[l] + cnt[r];// 次大值就从左边的次大值和右边的最大值里面选出sem[i] = Math.max(sem[l], sem[r]);}
}

这里就是 up 方法，父结点的最大值需要根据左右两边得到，次大值则是根据左右的最大值和次大值得到。

然后就是懒更新的逻辑。

public static void lazy(int i, int v) {if (v < max[i]) {sum[i] -= ((long) max[i] - v) * cnt[i];max[i] = v;}
}

懒更新需要判断当前更新的值是否要比原本的最大值要小，如果是才去更新，sum 直接更新为：((long) max[i] - v) * cnt[i]，然后 max 最大值更新为 v 就结束了，下面是代码，使用对数器验证。

public class Code03_SegmentTreeSetminQueryMaxSum1 {public static int MAXN = 100001;// 次大值的最小值, 原始数组范围假设是 -10000 - 10000，那么这个值可以设置为// 比 -10000 小的数public static int LOWEST = Integer.MIN_VALUE;// 原始数组public static int[] arr = new int[MAXN];// 累加和public static long[] sum = new long[MAXN << 2];// 最大值，维护了当前范围的最大值，同时又维护了懒更新信息public static int[] max = new int[MAXN << 2];// 最大值个数数组public static int[] cnt = new int[MAXN << 2];// 次大值数组public static int[] sem = new int[MAXN << 2];private static void up(int i) {int l = i << 1;int r = i << 1 | 1;// 左 + 右sum[i] = sum[l] + sum[r];// 左和右的最大值比较max[i] = Math.max(max[l], max[r]);// 如果最大值来自左边if (max[l] > max[r]) {// 父结点的最大值个数就跟左边一样cnt[i] = cnt[l];// 次大值就从左边的次大值和右边的最大值里面选出sem[i] = Math.max(sem[l], max[r]);// 如果最大值来自右边} else if (max[l] < max[r]) {// 父结点的最大值个数就跟右边一样cnt[i] = cnt[r];// 次大值就从左边的最大值和右边的次大值里面选出sem[i] = Math.max(max[l], sem[r]);} else {// 父结点的最大值个数就是左节点最大值个数 + 右节点最大值个数cnt[i] = cnt[l] + cnt[r];// 次大值就从左边的次大值和右边的最大值里面选出sem[i] = Math.max(sem[l], sem[r]);}}public static void down(int i) {// 将最大值的懒更新信息下发到左右节点lazy(i << 1, max[i]);lazy(i << 1 | 1, max[i]);}// 一定是没有颠覆掉次大值的懒更新信息下发，也就是说：// 最大值被压成v，并且v > 严格次大值的情况下// sum和max怎么调整public static void lazy(int i, int v) {if (v < max[i]) {sum[i] -= ((long) max[i] - v) * cnt[i];max[i] = v;}}public static void build(int l, int r, int i) {if (l == r) {// 初始化的时候最大值和累加和等于 arr[l]sum[i] = max[i] = arr[l];cnt[i] = 1;// 次大值就是最小值sem[i] = LOWEST;} else {int mid = (l + r) >> 1;build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}}public static void setMin(int jobl, int jobr, int jobv, int l, int r, int i) {if (jobv >= max[i]) {// 如果要更新的值比 max[i] 要大, 说明不需要更新, 直接返回return;}if (jobl <= l && r <= jobr && sem[i] < jobv) {// 如果当前节点需要懒更新, 必须要满足 sem[i] < jobv < max[i]lazy(i, jobv);} else {// 懒更新信息下发down(i);int mid = (l + r) >> 1;if (jobl <= mid) {setMin(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {setMin(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}// 汇总up(i);}}public static int queryMax(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return max[i];}down(i);int mid = (l + r) >> 1;int ans = Integer.MIN_VALUE;if (jobl <= mid) {ans = Math.max(ans, queryMax(jobl, jobr, l, mid, i << 1));}if (jobr > mid) {ans = Math.max(ans, queryMax(jobl, jobr, mid + 1, r, i << 1 | 1));}return ans;}public static long querySum(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];}down(i);int mid = (l + r) >> 1;long ans = 0;if (jobl <= mid) {ans += querySum(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += querySum(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}public static void main(String[] args) {System.out.println("测试开始");int n = 2000;int v = 5000;int t = 1000000;randomArray(n, v);int[] check = new int[n + 1];for (int i = 1; i <= n; i++) {check[i] = arr[i];}build(1, n, 1);for (int i = 1, op, a, b, jobl, jobr, jobv; i <= t; i++) {op = (int) (Math.random() * 3);a = (int) (Math.random() * n) + 1;b = (int) (Math.random() * n) + 1;jobl = Math.min(a, b);jobr = Math.max(a, b);if (op == 0) {jobv = (int) (Math.random() * v * 2) - v;setMin(jobl, jobr, jobv, 1, n, 1);checkSetMin(check, jobl, jobr, jobv);} else if (op == 1) {int ans1 = queryMax(jobl, jobr, 1, n, 1);int ans2 = checkQueryMax(check, jobl, jobr);if (ans1 != ans2) {System.out.println("出错了!");}} else {long ans1 = querySum(jobl, jobr, 1, n, 1);long ans2 = checkQuerySum(check, jobl, jobr);if (ans1 != ans2) {System.out.println("出错了!");}}}System.out.println("测试结束");}public static void randomArray(int n, int v) {for (int i = 1; i <= n; i++) {arr[i] = (int) (Math.random() * v * 2) - v;}}public static void checkSetMin(int[] check, int jobl, int jobr, int jobv) {for (int i = jobl; i <= jobr; i++) {check[i] = Math.min(check[i], jobv);}}public static int checkQueryMax(int[] check, int jobl, int jobr) {int ans = Integer.MIN_VALUE;for (int i = jobl; i <= jobr; i++) {ans = Math.max(ans, check[i]);}return ans;}public static long checkQuerySum(int[] check, int jobl, int jobr) {long ans = 0;for (int i = jobl; i <= jobr; i++) {ans += check[i];}return ans;}}

3. 线段树范围增加操作 + 区间最值操作

上面是区间最值操作，没有引入范围增加的，这里来看下引入范围增加之后势能的变化是怎么样的，时间复杂度又增加了多少。

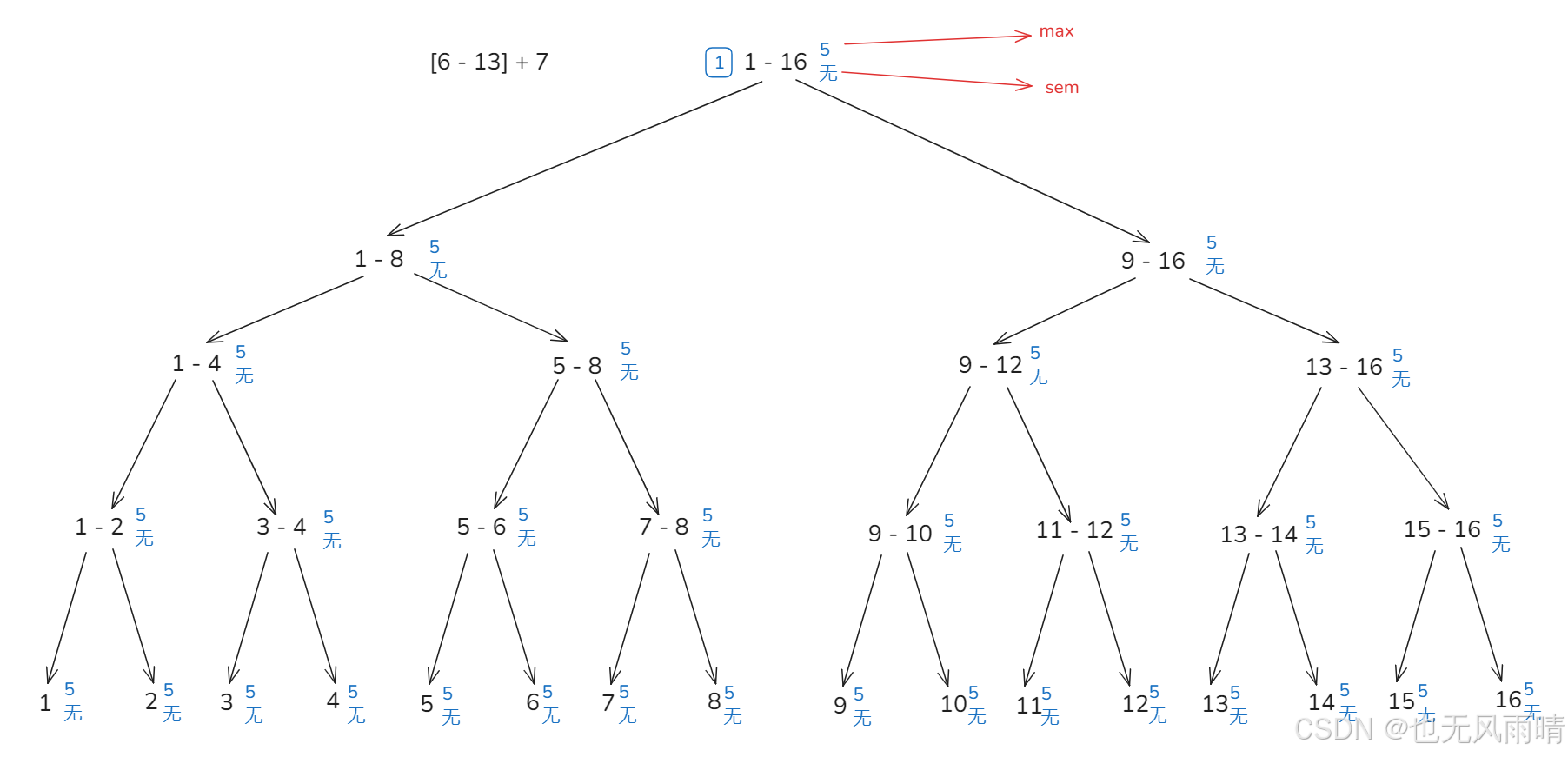
比如现在线段树就是上面的图示，现在要整体在 [6 - 13] + 7，假设现在每一次 +7 都深入到叶子节点，不懒更新，我们来看下增加之后的标签会变化成什么样。

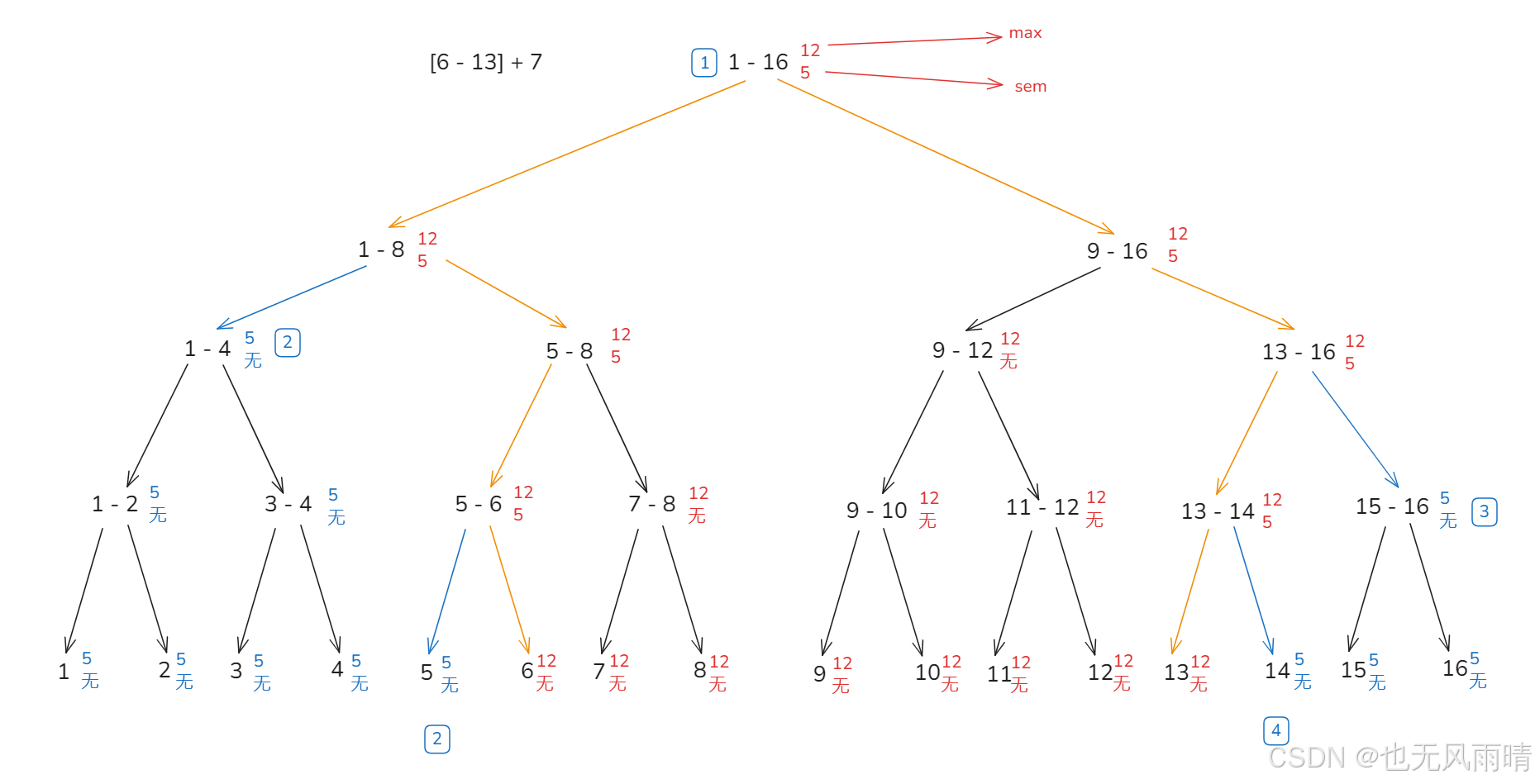
修改完了之后，可以看到黄色边线就是这个范围的左右边界，而标签就是蓝色边线的部分，可以看到标签就是在黄色边线产生的，中间像 9 - 12 这种全包住的范围是不会产生标签的，因此我们可以估算下，一次范围更新产生的标签是 $lo{g}_{2}n$，那么上面 2.2 小节也说了标签回收需要走过树高，也是 $lo{g}_{2}n$ 的时间复杂度，因此整体时间复杂度估算下来会增加 $lo{g}_{2}n\ast lo{g}_{2}n$，这个量是比较小的，对整体影响不大。

然后再来看下如果范围增加的情况下 max 和 sem 要如何变化。

• max：对于 max 数组，max[i] + v 就可以
• sem：对于 sem，需要判断是否等于 LOWEST，如果等于就不处理，否则 + v

sem 比较特殊，如果 sem 已经变成 LOWEST 了，那么说明这棵子树上面都已经统一了，比如说上面图的 9 - 12 节点，这种情况下左右节点范围里面的每一个值都是一样的，也就是都等于最大值，所以只需要更新最大值就好了，不需要更新次大值。

由于这次新增了 add 操作，所以最大值数组 max 就不用来维护懒信息了，新增两个数组 maxAdd 和 otherAdd，一个用于维护最大值新增的懒信息，一个用于除了最大值之外的其他值新增的懒信息。为什么要这两个数组呢，只用一个 add 数组维护新增的懒信息行不行呢？

不太够，比如上面 2.3 小节的 setMin 方法，假设 sem[i] < v < max[i]，这个方法在懒更新的时候 add[i] 会更新为 jobv - max[i]，最大值更新为 max[i] + v，但是 sem[i] += sem[i] == LOWEST ? 0 : add 就有问题，因为 sem 不需要加上 jobv - max[i]，这个 v 是大于 sem[i] 的。

// add 是 jobv - max[i]
public static void lazy(int i, int n, long v) {sum[i] += n * vmax[i] += v;// 次大值不需要加上这玩意, 因为 v > sem[i]sem[i] += sem[i] == LOWEST ? 0 : add;add[i] += v
}

因此需要用两个数组，一个表示最大值更新的幅度，一个表示次大值更新的服务，最终整体代码如下。

public class Main {public static int MAXN = 500001;public static long LOWEST = Long.MIN_VALUE;// 原始数组public static int[] arr = new int[MAXN];// 累加和信息public static long[] sum = new long[MAXN << 2];// 最大值信息, 只维护最大值, 不维护懒更新信息public static long[] max = new long[MAXN << 2];// 最大值个数public static int[] cnt = new int[MAXN << 2];// 严格次大值public static long[] sem = new long[MAXN << 2];// 最大值的懒更新信息public static long[] maxAdd = new long[MAXN << 2];// 除了最大值之外的其他值的懒更新信息public static long[] otherAdd = new long[MAXN << 2];public static void up(int i) {int l = i << 1;int r = i << 1 | 1;sum[i] = sum[l] + sum[r];max[i] = Math.max(max[l], max[r]);if (max[l] > max[r]) {cnt[i] = cnt[l];sem[i] = Math.max(sem[l], max[r]);} else if (max[l] < max[r]) {cnt[i] = cnt[r];sem[i] = Math.max(max[l], sem[r]);} else {cnt[i] = cnt[l] + cnt[r];sem[i] = Math.max(sem[l], sem[r]);}}// 懒更新public static void lazy(int i, int maxCnt, int otherCnt, long maxAddv, long otherAddv){// 最大值懒更新lazyAddMax(i, maxCnt, maxAddv);// 除了最大值之外的其他值的懒更新lazyAddOther(i, otherCnt, otherAddv);}public static void lazyAddMax(int i, int n, long maxValue){sum[i] += maxValue * n;max[i] += maxValue;maxAdd[i] += maxValue;}public static void lazyAddOther(int i, int n, long otherValue){sum[i] += otherValue * n;// 这里是关键sem[i] += sem[i] == LOWEST ? 0 : otherValue;otherAdd[i] += otherValue;}// 下发当前 i 节点的懒更新信息public static void down(int i, int ln, int rn) {int l = i << 1;int r = i << 1 | 1;// 这里先算出最大值是哪个, 因为当前 max[i] 很有可能是已经被懒更新过了// 如果直接用 tmp = max[i], 很有可能找不出左右哪个是最大值// 比如原来 max[i] = 10, 然后新增 +v 让这个范围的最大值 max[i] + v 了, 这种情况下由于懒住没有向下发, 因此左右节点的最大值就对不上了long tmp = Math.max(max[l], max[r]);if (max[l] == tmp) {// 懒更新左节点, 传入左节点的最大值范围长度(用于更新最大值), ln - cnt[l](用于更新其他值)lazy(l, cnt[l], ln - cnt[l], maxAdd[i], otherAdd[i]);} else {lazy(l, cnt[l], ln - cnt[l], otherAdd[i], otherAdd[i]);}if (max[r] == tmp) {lazy(r, cnt[r], rn - cnt[r], maxAdd[i], otherAdd[i]);} else {lazy(r, cnt[r], rn - cnt[r], otherAdd[i], otherAdd[i]);}maxAdd[i] = otherAdd[i] = 0;}public static void build(int l, int r, int i) {if (l == r) {sum[i] = max[i] = arr[l];sem[i] = LOWEST;cnt[i] = 1;} else {int mid = (l + r) >> 1;build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}maxAdd[i] = otherAdd[i] = 0;}public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {lazy(i, cnt[i], r - l + 1 - cnt[i], jobv, jobv);} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);if (jobl <= mid) {add(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {add(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}public static void setMin(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobv >= max[i]) {return;}if (jobl <= l && r <= jobr && sem[i] < jobv) {lazy(i, cnt[i], r - l + 1 - cnt[i], jobv - max[i], 0);} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);if (jobl <= mid) {setMin(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {setMin(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}public static long querySum(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);long ans = 0;if (jobl <= mid) {ans += querySum(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += querySum(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}}public static long queryMax(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return max[i];} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);Long ans = Long.MIN_VALUE;if (jobl <= mid) {ans = Math.max(ans, queryMax(jobl, jobr, l, mid, i << 1));}if (jobr > mid) {ans = Math.max(ans, queryMax(jobl, jobr, mid + 1, r, i << 1 | 1));}return ans;}}public static void main(String[] args) {System.out.println("测试开始");int n = 2000;int v = 5000;int t = 1000000;randomArray(n, v);long[] check = new long[n + 1];for (int i = 1; i <= n; i++) {check[i] = arr[i];}build(1, n, 1);for (int i = 1, op, a, b, jobl, jobr, jobv; i <= t; i++) {op = (int) (Math.random() * 4);a = (int) (Math.random() * n) + 1;b = (int) (Math.random() * n) + 1;jobl = Math.min(a, b);jobr = Math.max(a, b);if (op == 0) {jobv = (int) (Math.random() * v * 2) - v;add(jobl, jobr, jobv, 1, n, 1);checkAdd(check, jobl, jobr, jobv);} else if (op == 1) {jobv = (int) (Math.random() * v * 2) - v;setMin(jobl, jobr, jobv, 1, n, 1);checkSetMin(check, jobl, jobr, jobv);} else if (op == 2) {long ans1 = queryMax(jobl, jobr, 1, n, 1);long ans2 = checkQueryMax(check, jobl, jobr);if (ans1 != ans2) {System.out.println("出错了!");}} else {long ans1 = querySum(jobl, jobr, 1, n, 1);long ans2 = checkQuerySum(check, jobl, jobr);if (ans1 != ans2) {System.out.println("出错了!");}}}System.out.println("测试结束");}public static void randomArray(int n, int v) {for (int i = 1; i <= n; i++) {arr[i] = (int) (Math.random() * v * 2) - v;}}public static void checkAdd(long[] check, int jobl, int jobr, long jobv) {for (int i = jobl; i <= jobr; i++) {check[i] += jobv;}}public static void checkSetMin(long[] check, int jobl, int jobr, long jobv) {for (int i = jobl; i <= jobr; i++) {check[i] = Math.min(check[i], jobv);}}public static long checkQueryMax(long[] check, int jobl, int jobr) {long ans = Long.MIN_VALUE;for (int i = jobl; i <= jobr; i++) {ans = Math.max(ans, check[i]);}return ans;}public static long checkQuerySum(long[] check, int jobl, int jobr) {long ans = 0;for (int i = jobl; i <= jobr; i++) {ans += check[i];}return ans;}
}

这里不是课上的代码，直接用的对数器来验证，只是说如果我们将 maxAdd 和 otherAdd 分开来分别 lazy 就是这么写，但是这么写其实也能看到比较麻烦，那能不能将 lazyAddMax 和 lazyAddOther 合在一起呢，其实看逻辑没问题，因为这两部分的代码除了 sum 数组是都要更新之外，其他数组都是独立更新的，因此可以合成一个 lazy 方法，就是课程里面的代码。

public static void lazy(int i, int n, long maxAddv, long otherAddv) {// sum 数组等于最大值的更新加上除了最大值之外其他值的更新// 因为 cnt[i] 能表示最大值的个数, 所以可以直接在 O(1) 时间内算出 sum[i]sum[i] += maxAddv * cnt[i] + otherAddv * (n - cnt[i]);max[i] += maxAddv;sem[i] += sem[i] == LOWEST ? 0 : otherAddv;maxAdd[i] += maxAddv;otherAdd[i] += otherAddv;
}

整体代码如下：

import java.io.*;public class Main {public static int MAXN = 500001;public static long LOWEST = Long.MIN_VALUE;// 原始数组public static int[] arr = new int[MAXN];// 累加和信息public static long[] sum = new long[MAXN << 2];// 最大值信息, 只维护最大值, 不维护懒更新信息public static long[] max = new long[MAXN << 2];// 最大值个数public static int[] cnt = new int[MAXN << 2];// 严格次大值public static long[] sem = new long[MAXN << 2];// 最大值的懒更新信息public static long[] maxAdd = new long[MAXN << 2];// 除了最大值之外的其他值的懒更新信息public static long[] otherAdd = new long[MAXN << 2];public static void up(int i) {int l = i << 1;int r = i << 1 | 1;sum[i] = sum[l] + sum[r];max[i] = Math.max(max[l], max[r]);if (max[l] > max[r]) {cnt[i] = cnt[l];sem[i] = Math.max(sem[l], max[r]);} else if (max[l] < max[r]) {cnt[i] = cnt[r];sem[i] = Math.max(max[l], sem[r]);} else {cnt[i] = cnt[l] + cnt[r];sem[i] = Math.max(sem[l], sem[r]);}}public static void lazy(int i, int n, long maxAddv, long otherAddv) {sum[i] += maxAddv * cnt[i] + otherAddv * (n - cnt[i]);max[i] += maxAddv;sem[i] += sem[i] == LOWEST ? 0 : otherAddv;maxAdd[i] += maxAddv;otherAdd[i] += otherAddv;}// 下发当前 i 节点的懒更新信息public static void down(int i, int ln, int rn) {int l = i << 1;int r = i << 1 | 1;// 这里先算出最大值是哪个, 因为当前 max[i] 很有可能是已经被懒更新过了// 如果直接用 tmp = max[i], 很有可能找不出左右哪个是最大值// 比如原来 max[i] = 10, 然后新增 +v 让这个范围的最大值 max[i] + v 了, 这种情况下由于懒住没有向下发, 因此左右节点的最大值就对不上了long tmp = Math.max(max[l], max[r]);if (max[l] == tmp) {// 懒更新左节点, 传入左节点的最大值范围长度(用于更新最大值), ln - cnt[l](用于更新其他值)lazy(l, ln, maxAdd[i], otherAdd[i]);} else {lazy(l, ln, otherAdd[i], otherAdd[i]);}if (max[r] == tmp) {lazy(r, rn, maxAdd[i], otherAdd[i]);} else {lazy(r, rn, otherAdd[i], otherAdd[i]);}maxAdd[i] = otherAdd[i] = 0;}public static void build(int l, int r, int i) {if (l == r) {sum[i] = max[i] = arr[l];sem[i] = LOWEST;cnt[i] = 1;} else {int mid = (l + r) >> 1;build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}maxAdd[i] = otherAdd[i] = 0;}public static void add(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {// add 最大值和其他值都要 + jobvlazy(i, r - l + 1, jobv, jobv);} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);if (jobl <= mid) {add(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {add(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}public static void setMin(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobv >= max[i]) {return;}if (jobl <= l && r <= jobr && sem[i] < jobv) {// setMin 最大值 + jobv, 其他值不用增加lazy(i, r - l + 1, jobv - max[i], 0);} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);if (jobl <= mid) {setMin(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {setMin(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}public static long querySum(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);long ans = 0;if (jobl <= mid) {ans += querySum(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += querySum(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}}public static long queryMax(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return max[i];} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);Long ans = Long.MIN_VALUE;if (jobl <= mid) {ans = Math.max(ans, queryMax(jobl, jobr, l, mid, i << 1));}if (jobr > mid) {ans = Math.max(ans, queryMax(jobl, jobr, mid + 1, r, i << 1 | 1));}return ans;}}public static void main(String[] args) {System.out.println("测试开始");int n = 2000;int v = 5000;int t = 1000000;randomArray(n, v);long[] check = new long[n + 1];for (int i = 1; i <= n; i++) {check[i] = arr[i];}build(1, n, 1);for (int i = 1, op, a, b, jobl, jobr, jobv; i <= t; i++) {op = (int) (Math.random() * 4);a = (int) (Math.random() * n) + 1;b = (int) (Math.random() * n) + 1;jobl = Math.min(a, b);jobr = Math.max(a, b);if (op == 0) {jobv = (int) (Math.random() * v * 2) - v;add(jobl, jobr, jobv, 1, n, 1);checkAdd(check, jobl, jobr, jobv);} else if (op == 1) {jobv = (int) (Math.random() * v * 2) - v;setMin(jobl, jobr, jobv, 1, n, 1);checkSetMin(check, jobl, jobr, jobv);} else if (op == 2) {long ans1 = queryMax(jobl, jobr, 1, n, 1);long ans2 = checkQueryMax(check, jobl, jobr);if (ans1 != ans2) {System.out.println("出错了!");}} else {long ans1 = querySum(jobl, jobr, 1, n, 1);long ans2 = checkQuerySum(check, jobl, jobr);if (ans1 != ans2) {System.out.println("出错了!");}}}System.out.println("测试结束");}public static void randomArray(int n, int v) {for (int i = 1; i <= n; i++) {arr[i] = (int) (Math.random() * v * 2) - v;}}public static void checkAdd(long[] check, int jobl, int jobr, long jobv) {for (int i = jobl; i <= jobr; i++) {check[i] += jobv;}}public static void checkSetMin(long[] check, int jobl, int jobr, long jobv) {for (int i = jobl; i <= jobr; i++) {check[i] = Math.min(check[i], jobv);}}public static long checkQueryMax(long[] check, int jobl, int jobr) {long ans = Long.MIN_VALUE;for (int i = jobl; i <= jobr; i++) {ans = Math.max(ans, check[i]);}return ans;}public static long checkQuerySum(long[] check, int jobl, int jobr) {long ans = 0;for (int i = jobl; i <= jobr; i++) {ans += check[i];}return ans;}
}

4. 区间最值和历史最值问题

历史最值问题就是当前最大值范围曾经到过的最大值是多少，为了维护历史最大值，需要新增三个数组 maxHistory、maxAddTop、otherAddTop，分别表示历史最大值，maxAdd 的历史最大值，otherAdd 的历史最大值，下面还是用课上的例子演示下。

比如一开始 [1，8] 范围上的最大值是 100，次大值是 80，历史最大值也是 100，其他都是 0。

• 第一个操作 [1，8] 范围上 + 5，最大值更新为 105，次大值更新为 85，懒更新 maxAdd = 5，otherAdd = 2，历史最大值变成 105，maxAdd 历史最大值是 5，otherAdd 历史最大值是 5。
• 第二个操作 [1，8] 范围上 - 3，最大值更新为 102，次大值更新为 82，懒更新 maxAdd = 2，otherAdd = 2，历史最大值还是 105，maxAdd 历史最大值还是 5，otherAdd 历史最大值还是 5。
• 第三个操作 [1，8] 范围上设置最大值为 95，最大值更新为 95，次大值保持为 82，懒更新 maxAdd = 2 - 7 = -5，otherAdd 保持为 2，历史最大值还是 105，maxAdd 历史最大值还是 5，otherAdd 历史最大值还是 5。
• 第四个操作 [1，8] 范围上 + 20，最大值更新为 115，次大值更新为 102，懒更新 maxAdd = -5 + 20 = 15，otherAdd 保持为 2 + 20 = 22，历史最大值更新为 115，maxAdd 历史最大值更新为 15，otherAdd 历史最大值更新为 22。

上面就是整个流程，可以看到加入的三个数组都是用来保存历史最大值的，也就是曾经到过的最大的高度，那么此时需要将 1 - 8 的懒信息下发给子节点，如何更新。

假设 1 - 4 最大值是 100，次大值是 60，历史最大值是 100，现在 1 - 8 范围的懒更新下发到了 1 - 4，假设下面三个参数 maxAddv 是父结点的最大值懒信息，otherAddv 是父结点其他数的懒信息，maxUpv 是父结点的最大值的历史最大提升幅度的懒信息，otherUpv 是父结点历史其他值的最大提升幅度懒信息，更新如下：

1. 历史最大值更新为 maxHistory[i] = Math.max(maxHistory[i]，max[i] + maxUpv) = 115。
2. 历史最大值的最大幅度懒更新更新为：maxAddTop[i] = Math.max(maxAddTop[i], maxAdd[i] + maxUpv) = 15。
3. 历史其他值的最大幅度懒更新更新为：otherAddTop[i] = Math.max(otherAddTop[i], otherAdd[i] + otherUpv) = 22。
4. 最大值更新为：max[i] += maxAddv => max[i] = 115。
5. 次大值更新为：sem[i] += sem[i] == LOWEST ? 0 : otherAddv => sem[i] = 82。
6. 最大值懒更新信息更新为：maxAdd[i] += maxAddv => maxAdd[i] = 15。
7. 其他值懒更新信息更新为：otherAdd[i] += otherAddv => otherAdd[i] = 22。

再来看一个例子：

和上面第一个例子不同，假设 1 - 4 最大值是 80，次大值是 60，历史最大值是 80，意思就是现在这个范围不包括最大值了， 1 - 8 范围的懒更新下发到了 1 - 4，还是下面三个参数 maxAddv 、otherAddv 、maxUpv 、otherUpv，这时候下发过来的这几个参数 maxAddv = otherAddv = 父结点的 otherAddv = 22， maxUpv = otherUpv = 父结点的 otherUpv = 22。

1. 历史最大值更新为 maxHistory[i] = Math.max(maxHistory[i]，max[i] + maxUpv) = 102。
2. 历史最大值的最大幅度懒更新更新为：maxAddTop[i] = Math.max(maxAddTop[i], maxAdd[i] + maxUpv) = 22。
3. 历史其他值的最大幅度懒更新更新为：otherAddTop[i] = Math.max(otherAddTop[i], otherAdd[i] + otherUpv) = 22。
4. 最大值更新为：max[i] += maxAddv => max[i] = 102。
5. 次大值更新为：sem[i] += sem[i] == LOWEST ? 0 : otherAddv => sem[i] = 82。
6. 最大值懒更新信息更新为：maxAdd[i] += maxAddv => maxAdd[i] = 22。
7. 其他值懒更新信息更新为：otherAdd[i] += otherAddv => otherAdd[i] = 22。

这两个例子就是为了说明 maxAddv 和 maxUpv 是最大值才用的，如果当前范围最大值和父结点范围最大值不是一样的，那么就说明当前范围里面的数字都需要作为 other 处理，下面就是这部分更新的代码。

public static void lazy(int i, int n, long maxAddv, long otherAddv, long maxUpV, long otherUpv) {// 下面求历史的三个数组都依赖 max、maxAdd、otherAdd, 这三个数组放在后面更新// 历史最大值, 当前节点维护的最大值加上父亲节点下发下来的历史到过的最大幅度的值// 就是当前节点的最大值了maxHistory[i] = Math.max(maxHistory[i], max[i] + maxUpV);// 历史最大值增加的最大幅度懒新增信息maxAddTop[i] = Math.max(maxAddTop[i], maxAdd[i] + maxUpV);// 历史其他值增加的最大幅度懒新增信息otherAddTop[i] = Math.max(otherAddTop[i], otherAdd[i] + otherUpv);// 总和sum[i] += maxAddv * cnt[i] + otherAddv * (n - cnt[i]);// 最大值max[i] += maxAddv;// 次大值sem[i] += sem[i] == LOWEST ? 0 : otherAddv;// 最大值懒新增信息maxAdd[i] += maxAddv;// 其他值懒新增信息otherAdd[i] += otherAddv;
}

可以看到，由于 maxHistory、maxAddTop、otherAddTop 需要依赖其他 max、maxAdd、otherAdd 的原始数据，所以首先更新的就是这三个历史的数组，其实更新逻辑也很简单，比如历史最大值 maxHistory 就是通过当前节点现在维护的最大值加上父结点传下来的历史最大幅度信息求出来。再比如历史最大值增加的最大幅度懒新增信息，这个也是当前节点维护的最大值新增的懒信息加上父结点传下来的历史最大增加幅度懒信息，总的思想都是当前节点原来的值加上父结点传下来的历史的最大值求出来当前节点的历史最大值。

5. P6242 【模板】线段树 3（区间最值操作、区间历史最值）

题目链接：P6242 【模板】线段树 3（区间最值操作、区间历史最值）。

这道题就是上面第 4 节说的，维护区间最值和历史最值问题，代码直接贴出来。

import java.io.*;public class Main {public static int MAXN = 500001;// 最小值public static long LOWEST = Long.MIN_VALUE;// 原始数组public static int[] arr = new int[MAXN];// 总和数组public static long[] sum = new long[MAXN << 2];// 最大值数组public static long[] max = new long[MAXN << 2];// 最大值的数量public static int[] cnt = new int[MAXN << 2];// 次大值数组public static long[] sem = new long[MAXN << 2];// 最大值懒新增信息public static long[] maxAdd = new long[MAXN << 2];// 其他值懒新增信息public static long[] otherAdd = new long[MAXN << 2];// 历史最大值信息public static long[] maxHistory = new long[MAXN << 2];// 最大值历史到过的最大幅度public static long[] maxAddTop = new long[MAXN << 2];// 其他值历史到过的最大幅度public static long[] otherAddTop = new long[MAXN << 2];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));StreamTokenizer in = new StreamTokenizer(br);PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));in.nextToken();int n = (int) in.nval;in.nextToken();int m = (int) in.nval;for (int i = 1; i <= n; i++) {in.nextToken();arr[i] = (int) in.nval;}build(1, n, 1);long jobv;for (int i = 1, op, jobl, jobr; i <= m; i++) {in.nextToken();op = (int) in.nval;in.nextToken();jobl = (int) in.nval;in.nextToken();jobr = (int) in.nval;if (op == 1) {in.nextToken();jobv = (long) in.nval;add(jobl, jobr, jobv, 1, n, 1);} else if (op == 2) {in.nextToken();jobv = (long) in.nval;setMin(jobl, jobr, jobv, 1, n, 1);} else if (op == 3) {out.println(querySum(jobl, jobr, 1, n, 1));} else if (op == 4) {out.println(queryMax(jobl, jobr, 1, n, 1));} else {out.println(queryHistoryMax(jobl, jobr, 1, n, 1));}}out.flush();out.close();br.close();}private static long queryHistoryMax(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return maxHistory[i];}int mid = (l + r) >> 1;long ans = Long.MIN_VALUE;down(i, mid - l + 1, r - mid);if (jobl <= mid) {ans = Math.max(ans, queryHistoryMax(jobl, jobr, l, mid, i << 1));}if (jobr > mid) {ans = Math.max(ans, queryHistoryMax(jobl, jobr, mid + 1, r, i << 1 | 1));}return ans;}private static long queryMax(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return max[i];}int mid = (l + r) >> 1;long ans = Long.MIN_VALUE;down(i, mid - l + 1, r - mid);if (jobl <= mid) {ans = Math.max(ans, queryMax(jobl, jobr, l, mid, i << 1));}if (jobr > mid) {ans = Math.max(ans, queryMax(jobl, jobr, mid + 1, r, i << 1 | 1));}return ans;}private static long querySum(int jobl, int jobr, int l, int r, int i) {if (jobl <= l && r <= jobr) {return sum[i];}int mid = (l + r) >> 1;long ans = 0;down(i, mid - l + 1, r - mid);if (jobl <= mid) {ans += querySum(jobl, jobr, l, mid, i << 1);}if (jobr > mid) {ans += querySum(jobl, jobr, mid + 1, r, i << 1 | 1);}return ans;}private static void setMin(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobv >= max[i]) {return;}if (jobl <= l && r <= jobr && sem[i] < jobv) {// 懒更新, 最大值增加的幅度是 jobv - max[i], 次大值不需要管// 历史最大值增加的幅度也是 jobv - max[i]lazy(i, r - l + 1, jobv - max[i], 0, jobv - max[i], 0);} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);if (jobl <= mid) {setMin(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {setMin(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}private static void add(int jobl, int jobr, long jobv, int l, int r, int i) {if (jobl <= l && r <= jobr) {lazy(i, r - l + 1, jobv, jobv, jobv, jobv);} else {int mid = (l + r) >> 1;down(i, mid - l + 1, r - mid);if (jobl <= mid) {add(jobl, jobr, jobv, l, mid, i << 1);}if (jobr > mid) {add(jobl, jobr, jobv, mid + 1, r, i << 1 | 1);}up(i);}}private static void build(int l, int r, int i) {if (l == r) {// 累加和、最大值、历史最大值都等于原数组sum[i] = max[i] = maxHistory[i] = arr[l];// 次大值设置为 LOWESTsem[i] = LOWEST;cnt[i] = 1;} else {int mid = l + ((r - l) >> 1);build(l, mid, i << 1);build(mid + 1, r, i << 1 | 1);up(i);}maxAdd[i] = maxAddTop[i] = otherAdd[i] = otherAddTop[i] = 0;}private static void up(int i) {int l = i << 1;int r = i << 1 | 1;// 历史最大值从左右节点获取maxHistory[i] = Math.max(maxHistory[l], maxHistory[r]);sum[i] = sum[l] + sum[r];max[i] = Math.max(max[l], max[r]);if (max[l] > max[r]) {cnt[i] = cnt[l];sem[i] = Math.max(sem[l], max[r]);} else if (max[l] < max[r]) {cnt[i] = cnt[r];sem[i] = Math.max(max[l], sem[r]);} else {cnt[i] = cnt[l] + cnt[r];sem[i] = Math.max(sem[l], sem[r]);}}public static void down(int i, int ln, int rn) {int l = i << 1;int r = i << 1 | 1;// 先求出来左右节点的最大值, 设计到 add 操作父结点的最大值很有可能跟子节点不一样, 因此最大值从子节点中判断long temp = Math.max(max[l], max[r]);if (temp == max[l]) {// 懒更新, 如果最大值出在左节点, 那么就设置 maxAdd 和 maxAddToplazy(l, ln, maxAdd[i], otherAdd[i], maxAddTop[i], otherAddTop[i]);} else {// 懒更新, 如果最大值不出在左节点, 那么最大值懒更新幅度和最大值历史懒更新最大幅度都一样, 作为 other 来更新lazy(l, ln, otherAdd[i], otherAdd[i], otherAddTop[i], otherAddTop[i]);}// 右节点一样if (temp == max[r]) {lazy(r, rn, maxAdd[i], otherAdd[i], maxAddTop[i], otherAddTop[i]);} else {lazy(r, rn, otherAdd[i], otherAdd[i], otherAddTop[i], otherAddTop[i]);}// 四个懒信息全部置为 0maxAdd[i] = otherAdd[i] = maxAddTop[i] = otherAddTop[i] = 0;}// maxAddv   : 最大值增加多少// otherAddv : 其他数增加多少// maxUpv    : 最大值达到过的最大提升幅度// otherUpv  : 其他数达到过的最大提升幅度public static void lazy(int i, int n, long maxAddv, long otherAddv, long maxUpV, long otherUpv) {// 下面求历史的三个数组都依赖 max、maxAdd、otherAdd, 这三个数组放在后面更新// 历史最大值, 当前节点维护的最大值加上父亲节点下发下来的历史到过的最大值// 就是当前节点的最大值了maxHistory[i] = Math.max(maxHistory[i], max[i] + maxUpV);// 历史最大值增加的最大幅度懒新增信息maxAddTop[i] = Math.max(maxAddTop[i], maxAdd[i] + maxUpV);// 历史其他值增加的最大幅度懒新增信息otherAddTop[i] = Math.max(otherAddTop[i], otherAdd[i] + otherUpv);// 总和sum[i] += maxAddv * cnt[i] + otherAddv * (n - cnt[i]);// 最大值max[i] += maxAddv;// 次大值sem[i] += sem[i] == LOWEST ? 0 : otherAddv;// 最大值懒新增信息maxAdd[i] += maxAddv;// 其他值懒新增信息otherAdd[i] += otherAddv;}}

如有错误，欢迎指出！！！！